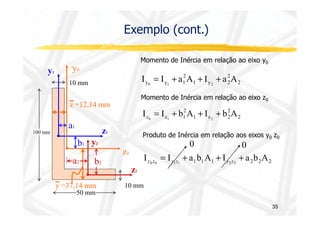
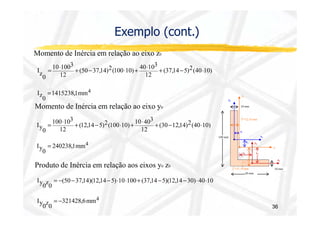
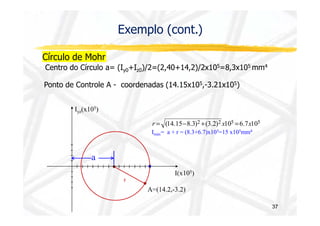
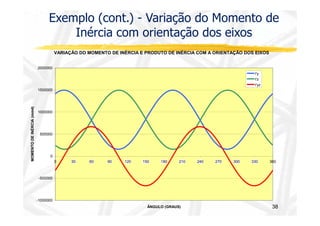
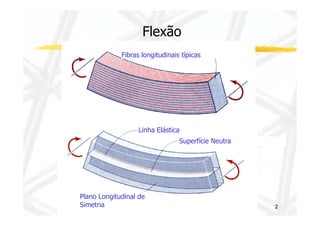
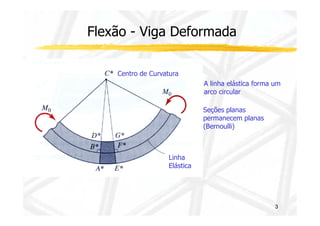
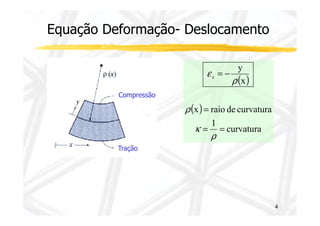
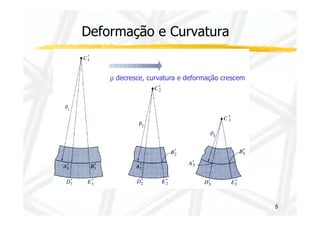
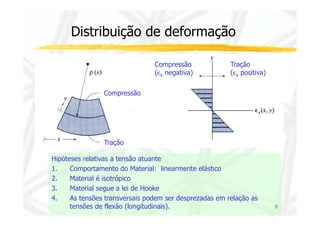
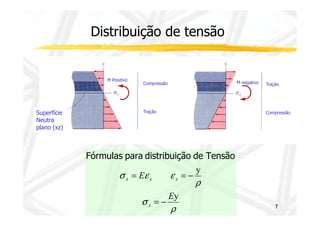
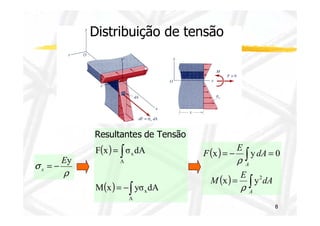
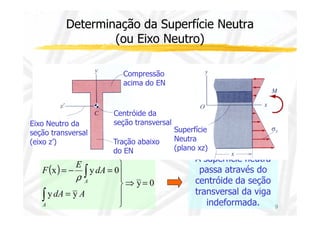
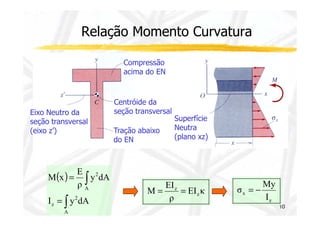
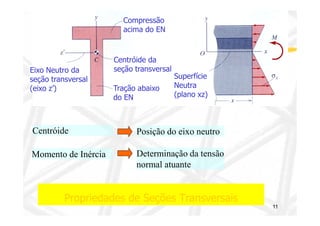
O documento discute conceitos de resistência dos materiais relacionados à flexão de vigas. As principais ideias apresentadas são: 1) a distribuição de tensões e deformações em uma viga sob flexão, com tração em uma face e compressão na outra; 2) o conceito de superfície neutra e como ele é relacionado ao centróide da seção transversal original; 3) como propriedades geométricas da seção transversal, como momento de inércia, influenciam a relação entre momento de flexão e curvatura.

1. RESISTÊNCIA DOS MATERIAIS
AULA 12 – Capítulo 6 – Flexão
1

2. Flexão
Fibras longitudinais típicas
2
Linha Elástica
Superfície Neutra
Plano Longitudinal de
Simetria

3. Flexão - Viga Deformada
A linha elástica forma um
arco circular
Seções planas
Centro de Curvatura
3
permanecem planas
(Bernoulli)
Linha
Elástica

4. Equação Deformação- Deslocamento
y
( x
)
( x )
=
raio de curvatura
= -
r
r
e x
Compressão
4
curvatura
1
= =
r
k
Tração

5. Deformação e Curvatura
r decresce, curvatura e deformação crescem
5

6. Distribuição de deformação
Compressão
Compressão
(ex negativa)
Tração
(ex positiva)
6
Tração
Hipóteses relativas a tensão atuante
1. Comportamento do Material: linearmente elástico
2. Material é isotrópico
3. Material segue a lei de Hooke
4. As tensões transversais podem ser desprezadas em relação as
tensões de flexão (longitudinais).

7. Distribuição de tensão
Superfície
Compressão
Tração
M Positivo
M negativo Tração
Compressão
Fórmulas para distribuição de Tensão
= = -
x x x
r 7
s
r
s e e
y
y
E
E
x
= -
Neutra
plano (xz)

8. Distribuição de tensão
x y 0
8
Resultantes de Tensão
( )
∫
=
F x σ dA
( ) = -
∫
A
x
A
x
M x yσ dA
( )
∫
( ) ∫
= - =
r
=
A
A
dA
E
M
dA
E
F
x y2
r
s Ey
r
x = -

9. Determinação da Superfície Neutra
(ou Eixo Neutro)
Compressão
acima do EN
Centróide da
9
( )
y 0
= - =
x y 0
y y
⇒ =

 

 

=
∫
∫
dA A
dA
E
F
A
A r
A superfície neutra
passa através do
centróide da seção
transversal da viga
indeformada.
seção transversal
Tração abaixo
do EN
Eixo Neutro da
seção transversal
(eixo z’)
Superfície
Neutra
(plano xz)

10. Relação Momento Curvatura
Compressão
acima do EN
Centróide da
seção transversal
Eixo Neutro da
10
Tração abaixo
do EN
seção transversal
(eixo z’)
Superfície
Neutra
(plano xz)
( )
∫
∫
=
=
A
E
2
z
A
2
I y dA
y dA
ρ
M x
= z =
M z
EI κ
EI
ρ
My
z
σ = -
x I

11. Compressão
acima do EN
Centróide da
seção transversal
Tração abaixo
do EN
Eixo Neutro da
seção transversal
(eixo z’)
Superfície
Neutra
(plano xz)
Propriedades de Seções Transversais
11
Centróide Posição do eixo neutro
Momento de Inércia Determinação da tensão
normal atuante

12. REVISÃO SOBRE CARACTERÍSTICAS
GEOMÉTRICAS DE SEÇÕES PLANAS
•Centróide de uma área
•Momento estático
•Momento de inércia (momentos de inércia, polar e
mmiissttoo))
•Teorema dos eixos paralelos
•Variação dos Momentos de inércia com orientação
dos eixos
12

13. Centróide de uma área
y
Coordenadas do centróide
=
∫A y dA
y
=
∫A z dA
z
13
z C ∫
z
z
y
dA
y
A dA
∫
A dA
Momento Estático (primeiro
momento da área)
= ∫ y dA z Q = ∫z dA y Q

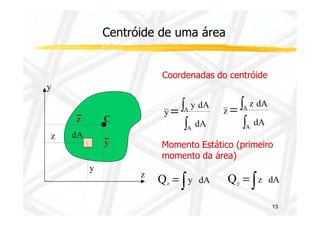
14. Centróide de uma área
Notas Importantes
•Eixos centrais - Eixos que passam pelo centróide da seção
•Dimensão do Momento Estático ⇒ [L]3
•Sinal do Momento Estático ⇒ Positivo, Negativo ou Nulo
14
•O Momento Estático relativo ao eixo central é nulo
Seções com Simetria
C C
Dupla
C
y C
z
Simples
C
Em relação a um
ponto

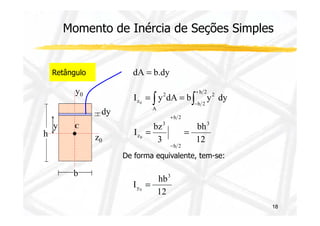
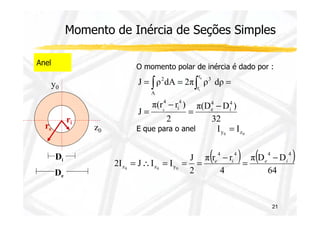
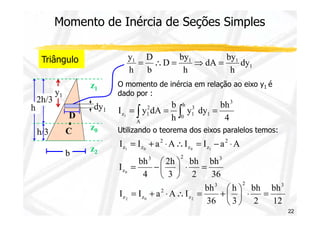
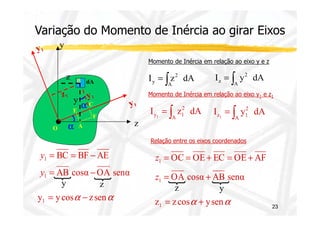
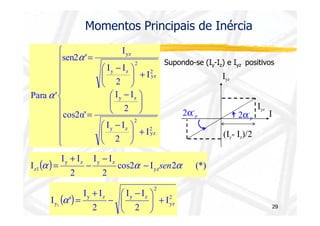
15. Momento de Inércia da Seção
Momento de Inércia em relação ao eixo y e z
y = ∫ I y dA
I z dA
A
2
A
2
z = ∫
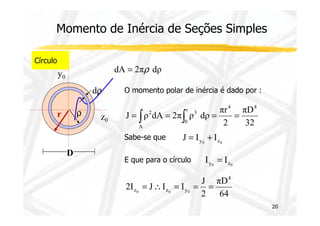
Momento de Polar de Inércia
J ρ dA
2 = ∫
A
y
z C
15
z
y
z dA
y
r
Sabemos porém que: r2 = y2 + z2
2 = ∫ +
J (y z2 ) dA
A
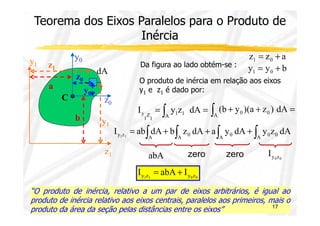
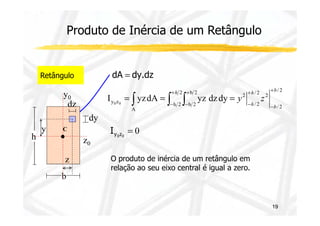
Produto de Inércia (Momento de Inércia
Misto)
Notas :
I yz dA
yz ∫A =
Dimensão - [L]4
Iy , Iz e J sempre positivos - Iyz positivo, negativo ou nulo

16. Teorema dos Eixos Paralelos (Steiner)
z0
y0
dA
y0
C
Da figura ao lado obtém-se : y y a 1 0 = +
O momento de inércia em relação ao eixo
y1 é dado por:
I = ∫ y dA =
A
2
z1 1
(a + y 2
∫ A
0
) dA =
y1
a y1
z1
2
2
z1 = ∫ + ∫ + ∫
I a dA 2ay dA y dA
A A 0 0
a2A zero
z0 I
z0
I 2
z1 = a A + I
A
“O momento de inércia, relativo a um eixo arbitrário, é igual ao momento de
inércia relativo ao eixo central, paralelo ao primeiro, mais o produto da área
da seção pelo quadrado da distância entre os eixos” 16

17. Teorema dos Eixos Paralelos para o Produto de
Inércia
Da figura ao lado obtém-se :
I = ∫ y z dA =
z z a 1 0 = +
O produto de inércia em relação aos eixos
y1 e z1 é dado por:
∫ (b + y )(a + z ) dA =
A 0 0
y0
dA
C
b
z1
y0
z0
a
y y b 1 0 = +
z0
y1
A 1 1
y
Z
1
1
I ab dA b z dA a y dA y z dA
y1z1 A A 0 A 0 A 0 0 = ∫ + ∫ + ∫ + ∫
abA zero y0z0 I
y1z1 y0z0 I = abA+ I
y1
z1
zero
“O produto de inércia, relativo a um par de eixos arbitrários, é igual ao
produto de inércia relativo aos eixos centrais, paralelos aos primeiros, mais o
produto da área da seção pelas distâncias entre os eixos” 17

18. Momento de Inércia de Seções Simples
Retângulo
y0
dy
dA = b.dy
h 2
z0 ∫ ∫+
I y dA b y dy
h 2
2
A
2
-
= =
18
C
h z0
b
y
bh
12
bz
3
I
3
h 2
h 2
3
+
z0 = =
-
De forma equivalente, tem-se:
hb
12
I
3
y0 =

19. Produto de Inércia de um Retângulo
Retângulo
y0
dA = dy.dz
/ 2
/ 2
/ 2 2
/ 2
2 2
y z I yzdA yz dz dy
h 2
b 2
b 2
A
0 0
b
b
h
h
h
y z
+
-
+
-
+
-
+
-
= ∫ = ∫ ∫ =
dy
dz
19
h z0
b
= 0 y0z0 I
O produto de inércia de um retângulo em
relação ao seu eixo central é igual a zero.
C
y
z

20. Momento de Inércia de Seções Simples
Círculo
dA = 2πr dρ
O momento polar de inércia é dado por :
2 r πr
4 3
πD
4 = ∫ = ∫ = =
J ρ dA 2π ρ dρ
z
y0
r
dr
r
20
32
2
0
A
Sabe-se que
E que para o círculo
z0
D
y0 z0 J = I + I
y0 z0 I = I
πD
64
J
2
2I J I I
4
z0 z0 y0 = = = =

21. Momento de Inércia de Seções Simples
Anel
O momento polar de inércia é dado por :
y0 J = ∫ ρ dA = 2π ∫ ρ dρ
=
π(r r ) π(D D )
J
4
i
4
e
4
i
4
r
r
3
A
2
e
e
i
=
-
-
=
E que para o anel
= = = = e - i π D D
= e -
i 21
2 32
z0
De
re
ri
Di ( ) ( )
64
π r r
4
J
2
2I J I I
4 4 4 4
z0 z0 y0
y0 z0 I = I

22. h
2h/3
Momento de Inércia de Seções Simples
Triângulo
by
y D
by
= = ⇒ =
1 1 1 dy
1
h
dA
h
D
b
h
O momento de inércia em relação ao eixo y1 é
dado por :
bh
z1 1 4
Utilizando o teorema dos eixos paralelos temos:
z = ∫ = ∫ y dy
=
b
h
I y dA
3
h 3
2
z1
D
y1
dy1
bh
12
bh
z1 z0 0 1 = + × = - ×
bh
bh
2h
bh

  = -
 = + × = +
z2 z0 2 × = 
2
h
3
bh
36
I I a A I
3 2 3
z
2


22
h/3 C
b
0 1
1
A
z0
z2
I I a A I I a2 A
z z
2
36
2
3
4
I
3 2 3
z0 = × 

23. Variação do Momento de Inércia ao girar Eixos
y
dA z
y
E
a C
F
Momento de Inércia em relação ao eixo y e z
y = ∫ I y dA
I z dA
A
2
A
2
z = ∫
Momento de Inércia em relação ao eixo y1 e z1
y1 A 1
∫ y I z2 dA
y = I y2 dA
z = ∫
1
B
23
a A
z
O
z z1 A Relação entre os eixos coordenados
OC OE EC OE AF 1 z = = + = +
OA cosα AB senα 1 z = +
z y
BC BF AE 1 y = = -
AB cosα OA senα 1 y = -
y z
y y cosa z sena 1 = - z z cosa ysena 1 = +

24. Variação do Momento de Inércia ao girar Eixos
Relação entre os eixos coordenados
y y cosa z sena 1 z z cosa ysena = - 1 = +
Momento de Inércia em relação ao eixo y1
y1 1 = ∫ = ∫ +
I z 2
dA (z cosα ysen α)2 dA
A A
y1 = ∫ + ∫ + ∫
2 2
2 2
I cos α z dA 2senαcosα yz dA sen α y dA
A
A A
24
Iy Iyz Iz
y1 = y + 2
+
I I cos α I z
sen α 2I yz
cosαsenα 2
Utilizando-se as seguintes relações trigonométricas, obtém-se:
cos 2 = + 2 1 - cos2α
α = =
y z y z
1 cos2α
y1 +
I yz
cos2α I sen2α
I I
2
I I
2
-
+
+
=
; 2cosαsenα sen2α
2
; sen α
2

25. Variação do Momento de Inércia ao girar Eixos
Relação entre os eixos coordenados
y y cosa z sena 1 = -
Momento de Inércia em relação ao eixo z1
z1 1 = ∫ = ∫ -
I y 2
dA (y cosα zsen α)2 dA
A A
I cos2α y2 dA 2senαcosα yz dA sen2α z2 dA
= ∫ - ∫ + ∫
25
2 2
2 2
cos α y sen α z A
A A
z1 Iz Iyz Iy
z1 = z + 2
-
I I cos α I y
sen α 2I yz
cosαsenα 2
Utilizando-se as seguintes relações trigonométricas, obtém-se:
cos 2 = + 2 1 - cos2α
α = =
y z z y
1 cos2α
z1 -
I yz
cos2α I sen2α
I I
2
I I
2
-
+
+
=
; 2cosαsenα sen2α
2
; sen α
2

26. Variação do Produto de Inércia ao girar Eixos
Relação entre os eixos coordenados
y y cosa z sena 1 z z cosa ysena = - 1 = +
(y z )(z y )dA
A
Produto de Inércia
I y z dA cosa sena cosa sena
y1z1 A 1 1 = ∫ = ∫ - +
I senαcosα z dA (cos α sen α) yz dA senαcosα y dA
y1z1 = - ∫ + - ∫ + ∫
A
2
2 2 2
A A
Iy Iyz Iz
26
I (I I )(cosαsen ) I (cos2α sen2α)
y1z1 z y yz = - a + -
Utilizando-se as seguintes relações trigonométricas, obtém-se:
cos α 2 = + 2 = - =
-
z y
1 cos2α
1 cos2α
y1z1 +
I yz
sen2α I cos2α
I I
2
=
; 2cosαsenα sen2α
2
; sen α
2

27. Resumo das Principais Relações
y z y z
y1 +
I yz
cos2α I sen2α (*)
I I
2
I I
2
-
+
+
=
y z y z
z1 -
I yz
cos2α I sen2α (**)
I I
2
I I
2
-
-
+
=
-
27
y z
y1z1 +
I yz
sen2α I cos2α (***)
I I
2
= -
O momento polar de inércia é dado por :
y1 z1 J = I + I
Somando-se (*) com (**), tem-se :
1 1 = + = +
y z y z J I I I I

28. y z y z
z1 -
I yz
cos2α I sen2α (*)
I I
2
I I
2
-
-
+
=
Momentos Principais de Inércia
Eixos principais de inércia são aqueles para os quais os momentos
de inércia Iy1 e Iz1 assumem valores máximos e mínimos
Derivando-se a expressão acima em relação a a e igualando-se a zero
28

 -
=
z1 y z - =  
sen2α 2I cos2α 0
I I
2
2
dI
dα
yz

 


 
I
yz
 -
 
=
I I
2
2
y z
p tg a
I
Iyz
Iyz
2a’
p
(Iy- Iz)/2
2a”
p

29. 


    


 

 -
yz
I I
 -
  
=

+  
 
=
I I
y z
2
yz
2
y z
2
cos2α'
I
2
I
sen2 '
Para '
a
a
Momentos Principais de Inércia
Supondo-se (Iy-Iz) e Iyz positivos
I
Iyz
Iyz
2a”
2a’
29
   

+  
 -
 
2
yz
2
I I
y z I
2
I I
I I
( ) y z y z
cos2 I 2 (*)
z1 a a - sen a
I yz
2
2
-
-
+
=
 -
I I
I I

( ) 2
yz
2
y z y z
1 +  
y I
2
2
I '

 

-
+
a =
p
(Iy- Iz)/2
p

30. Momentos Principais de Inércia
Supondo-se (Iy-Iz) e Iyz positivos

    



 
yz

- I
 -
I I
 -
-
 
+  
 
=
I I
y z
2
yz
2
y z
2
I
2
sen2 "
Para "
a
a
I
Iyz
Iyz
2a ” p
2a’
30
    


+  
 -
 
=
2
yz
2
I I
y z I
2
cos2a "
I I
I I
( ) y z y z
cos2 I 2 (*)
z1 a a - sen a
I yz
2
2
-
-
+
=
( ) 2
yz
2
 -
I I
I I
y z y z

" I +  
z1 I
2
2

 

+
+
a =
p
(Iy- Iz)/2

31. Momentos Principais de Inércia
Notas Importantes
•Para a’ e a” o produto de inércia Iy1z 1 é zero
•O produto de inércia em relação a qualquer eixo de simetria é zero
•Qualquer eixo de simetria representa um eixo principal de inércia
•Os momentos principais de inércia e suas respectivas orientações
podem ser determinadas de forma conveniente através de um processo
gráfico conhecido por Círculo de Mohr
31

32. Círculo de Mohr para Momentos de Inércia
y z y z
z1 a - sen a
I yz
cos2 I 2 (**)
I I
2
I I
2
-
= -
+
-
-
y z
y1z1 = - sen
a + a
I yz
2 I cos 2 (***)
I I
2
Elevando-se ambas equações ao quadrado e somando-as :
a r
32
2
yz
2
 -
= +  

I I
2 y z
y z
2
 +
I I
y z

z I
2
I
2
I
1 1 1 +  

 


 

-
ou
( ) 2
I - a + I 2 y z
= r
2
z1 1 1
Equação do Círculo
( )2 ( )2 2 x - a + y - b = r
b
x
y
a
r
Iy1
Iy1z1

33. Exemplo
10 mm
Determinação do centróide de áreas
compostas - Procedimento
•Estabelecer um sistema de eixos y, z
•Decompor em áreas simples
•Determinar centróide das áreas simples
•Calcular centróide da seção composta
33
50 mm
100 mm
10 mm

34. Exemplo
A1
10 mm
y
y1
∫ +∫
=
y dA y dA
y dA
z1 ∫
∫ +∫
=∫
A2
2
A1
1
A2
2
A1
1
dA dA
dA
y
37,14mm
=
× × + × ×
100 10 50 40 10 5
y =
× + ×
100 10 40 10
10 mm
50 mm
y1
∫ +∫
=
z dA z dA
∫ + ∫
z dA
∫
= × × + × ×
100 10 5 40 10 30
z =
× + ×
34 A2
100 mm
z
z1
y2
z2
y2
z2
12,14mm
100 10 40 10
= ∫
A2
2
A1
1
A2
2
A1
1
dA dA
dA
z

35. Exemplo (cont.)
y1 y0
10 mm
z =12,14 mm
Momento de Inércia em relação ao eixo y0
2
2
0 1 2 = + + +
1 y 2
2
y y 1 I I a A I a A
Momento de Inércia em relação ao eixo z0
I = I + b2A + I + b2A
Produto de Inércia em relação aos eixos y0 z0
35
y2
50 mm
100 mm
10 mm
z1
a1
b1
z0
y =37,14 mm
z2
a2 b2
2
2
1 z 2
2
z 1 b A b A
0 1 2 z
0 0
0 0 1 1 2 2 = + + + y z y z y z
1 1 1 2 2 2 I I a b A I a b A

36. Momento de Inércia em relação ao eixo z0
40 103 (50 37,14)2(100 10)
10 1003
z0 I = × + - × + × + - ×
1415238,1mm4
z0 I =
(37,14 5)2(40 10)
12
12
Exemplo (cont.)
Momento de Inércia em relação ao eixo y0
10 mm
y1
y0
36
10 403 (12,14 5)2(100 10)
100 103
y0 I = × + - × + × + - ×
240238,1mm4
y0 I =
(30 12,14)2(40 10)
12
12
Produto de Inércia em relação aos eixos y0 z0
y0z0 I = - - - × × + - - × ×
321428,6mm4
y0z0 I = -
(50 37,14)(12,14 5) 10 100 (37,14 5)(12,14 30) 40 10
50 mm
100 mm
10 mm
z1
a1
b1
z0
z =12,14 mm
y =37,14 mm
y2
z2
b2 a2

37. Exemplo (cont.)
Círculo de Mohr
Centro do Círculo a= (Iy0+Iz0)/2=(2,40+14,2)/2x105=8,3x105 mm4
Ponto de Controle A - coordenadas (14.15x105,-3.21x105)
Iyz(x105)
37
x10 )
r = (14.15-8.3)2 +(3.2)2 x105 =6.7x105
I(x105)
r
Imáx= a + r = (8.3+6.7)x105=15 x105mm4
A=(14.2,-3.2)
a

38. Exemplo (cont.) - Variação do Momento de
Inércia com orientação dos eixos
VARIAÇÃO DO MOMENTO DE INÉRCIA E PRODUTO DE INÉRCIA COM A ORIENTAÇÃO DOS EIXOS
2000000
1500000
1000000
MOMENTO DE INÉRCIA (mm4)
I'y
I'z
I'yz
38
500000
0
-500000
-1000000
0 30 60 90 120 150 180 210 240 270 300 330 360
ÂNGULO (GRAUS)

39. 7,0E+05
6,0E+05
5,0E+05
4,0E+05
3,0E+05
2,0E+05
1,0E+05
0,0E+00
0,0E+0
-1,0E+05
-2,0E+05
-3,0E+05
-4,0E+05
-5,0E+05
-6,0E+05
-7,0E+05
0
1,0E+0
5
2,0E+0
5
3,0E+0
5
4,0E+0
5
5,0E+0
5
6,0E+0
5
7,0E+0
5
8,0E+0
5
9,0E+0
5
1,0E+0
6
1,1E+0
6
1,2E+0
6
1,3E+0
6
1,4E+0
6
1,5E+0
6
1,6E+0
6
1,7E+0
6
1,8E+0
6
1,9E+0
6
2,0E+0
6
2,1E+0
6
2000000
1500000
I'y
I'yz
1000000
500000
0
-500000
0 30 60 90 120 150 180 210 240 270 300 330 360
-1000000 39
ÂNGULO (GRAUS)