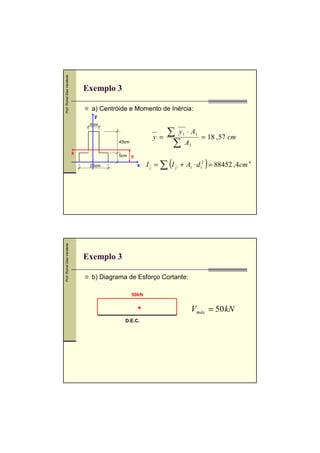
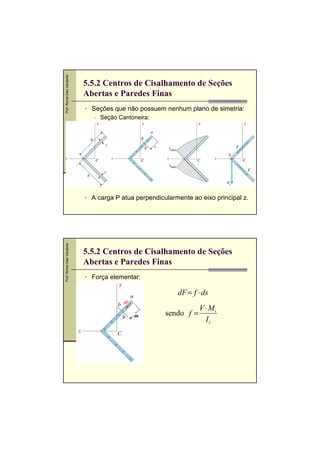
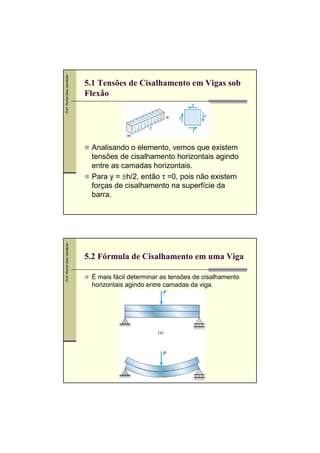
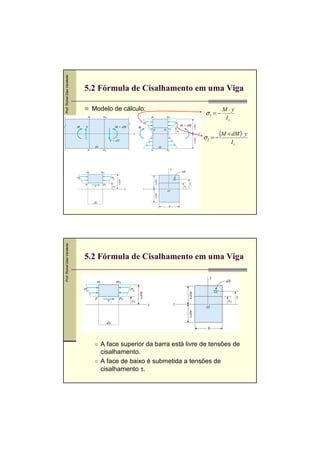
O documento descreve os conceitos de tensões de cisalhamento em vigas sob flexão. Discute as hipóteses básicas, a fórmula de cisalhamento e a distribuição das tensões de cisalhamento em seções retangulares e circulares. Também apresenta exemplos numéricos de dimensionamento de seções sob tensões de cisalhamento e flexão.











![Prof. Romel Dias Vanderlei
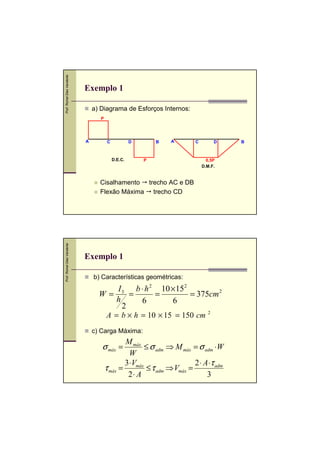
5.3.1 Tensão de Cisalhamento na Alma
Logo:
τ=
[ (
V ⋅ Ms
V
=
⋅ b ⋅ h2 − h12 + t ⋅ h12 − 4 ⋅ y12
t ⋅ Iz
8⋅t ⋅ Iz
) (
)]
b ⋅ h3 (b − t ) ⋅ h13 1
3
3
onde: I z =
−
= ⋅ b ⋅ h3 − b ⋅ h1 + t ⋅ h1
12
12
12
Prof. Romel Dias Vanderlei
(
5.3.2 Tensões de Cisalhamento Máximas e
Mínimas
τmáx ocorre na Linha Neutra, y1 = 0.
τmín ocorre no encontro alma-flange, y1 = ±h1/2.
Logo:
[
τ máx =
V
⋅ b ⋅ h2 − b ⋅ h12 + t ⋅ h12
8⋅t ⋅ I z
τ mín =
V
⋅ h2 − h12
8⋅ t ⋅ I z
[
]
]
)](https://image.slidesharecdn.com/capitulo5-cisalhamento-131213142517-phpapp02/85/Cisalhamento-15-320.jpg)