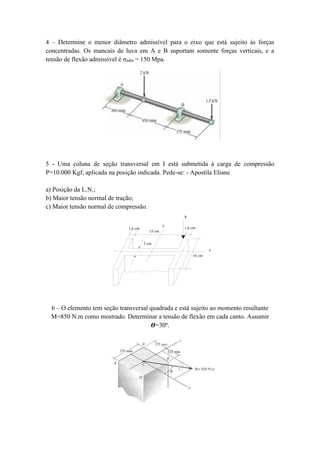
O documento apresenta uma lista de exercícios de resistência dos materiais sobre flexão. Os alunos devem realizar os exercícios 2, 4, 5, 7 e 8 que envolvem determinar esforços de flexão, tensões máximas, posição da linha neutra e diâmetro de eixos sob carga.

1. Resistência dos Materiais Avançado
Lista de Exercícios de Flexão
Prof. Larissa Rocha Pereira
Entregar exercícios: 2, 4, 5, 7 e 8
1 – Foram propostas duas soluções para o projeto de uma viga. Determinar qual delas
suportará um momento M=150 kN.m com o menor esforço de flexão.
2 – A peça de máquina de alumínio está sujeita a um momento M= 75 N.m. Determinar
os esforços de flexão máximos de tração e de compressão na peça.
3 – A área da seção transversal da escora de alumínio tem forma de cruz. Se ela for
submetida ao momento M = 8kN.m, determine a tensão de flexão máxima na viga e no
ponto B.

2. 4 – Determine o menor diâmetro admissível para o eixo que está sujeito às forças
concentradas. Os mancais de luva em A e B suportam somente forças verticais, e a
tensão de flexão admissível é σadm = 150 Mpa.
5 - Uma coluna de seção transversal em I está submetida à carga de compressão
P=10.000 Kgf, aplicada na posição indicada. Pede-se: - Apostila Eliane
a) Posição da L.N.;
b) Maior tensão normal de tração;
c) Maior tensão normal de compressão.
10 cm
15 cm
1,6 cm1,6 cm
2 cm
y
P
x
6 – O elemento tem seção transversal quadrada e está sujeito ao momento resultante
M=850 N.m como mostrado. Determinar a tensão de flexão em cada canto. Assumir
𝜭=30º.

3. 7 – O momento M é aplicado a uma viga de seção transversal mostrada, em um plano
formando um ângulo 𝛽 com a vertical. Determinar: (a) a tensão no ponto A; (b) a tensão
no ponto B; (c) o ângulo que a linha neutra forma com o plano horizontal.
8- O momento resultante que atua sobre a seção transversal do suporte de alumínio tem
intensidade M=520 N.m e a direção mostrada. Determinar a tensão de flexão máxima
no suporte (pontos A e B). Especificar também a orientação do eixo neutro.
Respostas
1) 𝜎𝐴 = 114,5 𝑀𝑃𝑎 ; 𝜎 𝐵 = 74,6 𝑀𝑃𝑎; 𝐿𝑒𝑡𝑟𝑎 b
2) 𝜎𝑡 =6,70 MPa; 𝜎𝑐 =3,6 MPa
3) 𝜎 𝑚𝑎𝑥 =49,4 MPa; 𝜎 𝐵 =4,49 MPa
4) d= 33,67 mm
5) 𝜎𝑡 =988,8 Kgf/cm²; 𝜎𝑐 =- 1311 kgf/cm²
6) 𝜎𝐴 = −119 𝑘𝑃𝑎, ; 𝜎 𝐵 = 446 𝑘𝑃𝑎, ; 𝜎 𝐷 = −446 𝑘𝑃𝑎, ; 𝜎 𝐸 = 119 𝑘𝑃𝑎
7) 𝜎𝐴 = 115 𝑀𝑃𝑎; 𝜎 𝐵 = −76,4 𝑀𝑃𝑎; 𝛼 = 79,7°
8) σA = −1.3Mpa; σB = 0.587Mpa; α = 3.72º