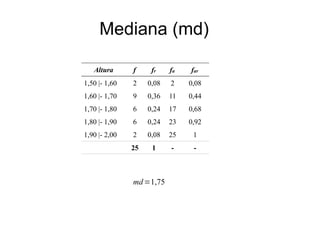
O documento discute sobre estatística, definindo-a como uma ciência que envolve a coleta, organização, resumo, análise e interpretação de dados. Apresenta também as principais medidas resumo como média, mediana e moda, definindo-as e ilustrando seus cálculos em diferentes conjuntos de dados.

1. O que é Estatística?
A Estatística é uma ciência que envolve
coleta, organização, resumo, análise e
interpretação dos dados.

2. Se te perguntam quanto tempo
um ônibus demora para passar...

3. Você apresenta uma tabela de frequências?Você apresenta uma tabela de frequências?
Ou dá uma resposta breve?
Que sintetize a informação desejada?

4. Medidas Resumo
Definição
Medidas resumo são valores numéricos obtidos a partir de
uma amostra que:
~ resumem a informação contida nos dados;
~ exibem o comportamento da distribuição da amostra:
valores centrais, valores extremais, dispersão, assimetria,
entre outros.

5. Medidas De Tendência Central
Média
Mediana
Moda

6. Média (x)
É a a razão entre o somatório dos dados e o total das
frequências (n).
_
Onde x1
, x2
, ... representam cada um dos dados.

7. Média (x)
_
Suponha que parafusos a serem utilizados em tomadas
elétricas são embalados em caixas rotuladas como contendo
100 unidades. Em uma construção, 10 caixas de um lote
tiveram o número de parafusos contados, fornecendo os
valores 98, 102, 100, 100, 99, 97, 96, 95, 99, 100. Para essas
caixas, o número médio de parafusos será dado por:

8. Idade f fr fa far
17 2 0,08 2 0,08
18 9 0,36 11 0,44
19 6 0,24 17 0,68
20 6 0,24 23 0,92
21 2 0,08 25 1
25 1 - -
̄x=
17+ 17+ 18+ 18+ 18+ ...+ 21+ 21
25
≈18,9
̄x=
17⋅2+ 18⋅9+ ...+ 21⋅2
25
≈18,9
Média (x)
_

9. Altura f fr fa far
1,50 |- 1,60 2 0,08 2 0,08
1,60 |- 1,70 9 0,36 11 0,44
1,70 |- 1,80 6 0,24 17 0,68
1,80 |- 1,90 6 0,24 23 0,92
1,90 |- 2,00 2 0,08 25 1
25 1 - -
E se os dados estiverem agrupados em classes?
Dados em classes: consideramos a média da classe:
̄x=
1,55⋅2+ 165⋅9+ ...+ 1,95⋅2
25
≈1,74
Média (x)
_

10. Mediana (md)
É o valor que ocupa a posição central dos dados ordenados.
No exemplo dos parafusos temos que ordenar os dados 98,
102, 100, 100, 99, 97, 96, 95, 99, 100:
95, 96, 97, 98, 99, 99, 100, 100, 100, 102.
Como a quantidade de elementos é par, a mediana é igual à
média dos dois valores centrais (99 e 99):
md=
(99+ 99)
2
=99

11. Mediana (md)
Idade f fr fa far
17 2 0,08 2 0,08
18 9 0,36 11 0,44
19 6 0,24 17 0,68
20 6 0,24 23 0,92
21 2 0,08 25 1
25 1 - -
São 25 dados, o do meio é o 13º. Olhando a frequência
acumulada, vemos que o 13º é 19.

12. Mediana (md)
md=1,75
Altura f fr fa far
1,50 |- 1,60 2 0,08 2 0,08
1,60 |- 1,70 9 0,36 11 0,44
1,70 |- 1,80 6 0,24 17 0,68
1,80 |- 1,90 6 0,24 23 0,92
1,90 |- 2,00 2 0,08 25 1
25 1 - -

13. Moda (mo)
É o dado que tem a maior frequência.
Idade f fr fa far
17 2 0,08 2 0,08
18 9 0,36 11 0,44
19 6 0,24 17 0,68
20 6 0,24 23 0,92
21 2 0,08 25 1
25 1 - -
mo=18
Altura f fr fa far
1,50 |- 1,60 2 0,08 2 0,08
1,60 |- 1,70 9 0,36 11 0,44
1,70 |- 1,80 6 0,24 17 0,68
1,80 |- 1,90 6 0,24 23 0,92
1,90 |- 2,00 2 0,08 25 1
25 1 - -
mo=1,65

14. A média é a medida de tendência central mais comum;
Como a méida é muito influenciada por valores discrepantes, a
mediana é mais aconselhável para esses casos.
A moda é a única medida de tendência central que se aplica a
dados qualitativos nominais.

15. Por enquanto, é só.