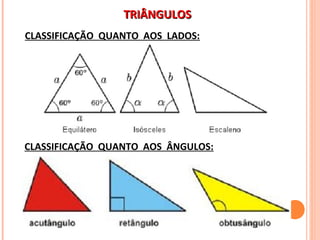
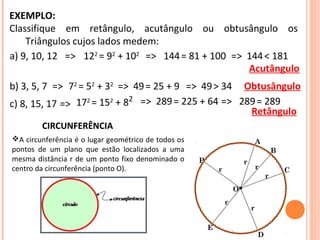
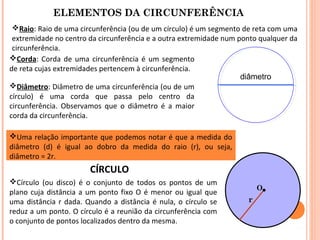
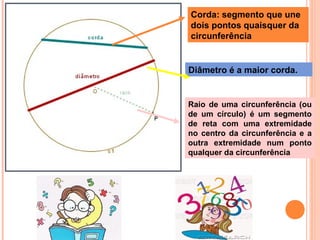
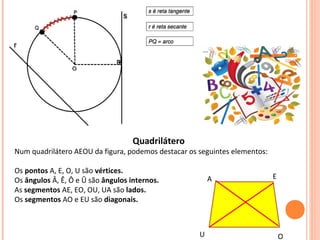
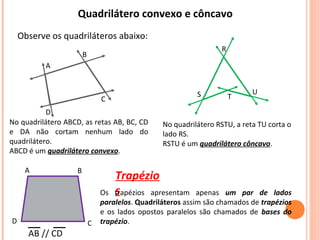
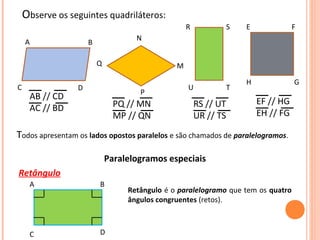
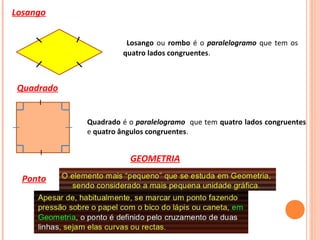
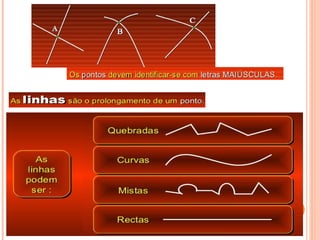
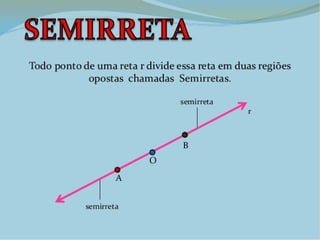
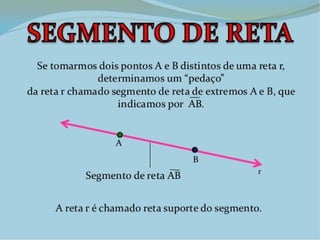
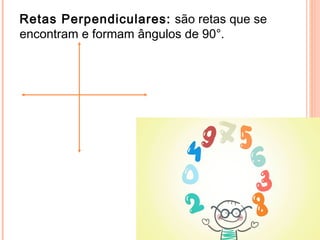
O documento discute triângulos e suas classificações de acordo com os ângulos e lados. É apresentada a classificação de triângulos em agudângulo, retângulo e obtusângulo e fornecidas fórmulas para determinar o tipo de triângulo a partir das medidas dos lados. Circunferências e seus elementos como raio, diâmetro e corda também são explicados.

1. MATEMÁTICA – ENSINO FUNDAMENTALMATEMÁTICA – ENSINO FUNDAMENTAL
AULA 3AULA 3

2. TRIÂNGULOSTRIÂNGULOS
CLASSIFICAÇÃO QUANTO AOS LADOS:
CLASSIFICAÇÃO QUANTO AOS ÂNGULOS:

3. ACUTÂNGULO: Os três ângulos são agudos
RETÂNGULO: Dois ângulos agudos e um ângulo reto.
OBTUSÂNGULO: Um ângulo obtuso e dois ângulos agudos
> 90° e < 180° - obtusângulo
NATUREZA DE UM TRIÂNGULO
O triângulo retângulo: a2
= b2
+ c2
O triângulo acutângulo: a2
< b2
+ c2
O triângulo obtusângulo: a2
> b2
+ c2
Exemplo:Exemplo: Classifique o triângulo cujas medidas são:
a = 15 cm, b = 12 cm e c = 10 cm.
Solução:
a2
= b2
+ c2
152
= 122
+ 102
225= 144 + 100
225< 244 Podemos afirmar que o triângulo é Acutângulo.
=> =>

4. EXEMPLO:
Classifique em retângulo, acutângulo ou obtusângulo os
Triângulos cujos lados medem:
a) 9, 10, 12 => 122
= 92
+ 102
=> 144= 81 + 100 144< 181
Acutângulo
b) 3, 5, 7 72
= 52
+ 32
49= 25 + 9 49> 34 Obtusângulo
c) 8, 15, 17 => 172
= 152
+ 82 289= 225 + 64 289= 289
Retângulo
=>
=> => =>
=> =>
A circunferência é o lugar geométrico de todos os
pontos de um plano que estão localizados a uma
mesma distância r de um ponto fixo denominado o
centro da circunferência (ponto O).
O
A
B
C
D
E
P
r
r
r
r
r
r
CIRCUNFERÊNCIA

5. ELEMENTOS DA CIRCUNFERÊNCIA
Raio: Raio de uma circunferência (ou de um círculo) é um segmento de reta com uma
extremidade no centro da circunferência e a outra extremidade num ponto qualquer da
circunferência.
Corda: Corda de uma circunferência é um segmento
de reta cujas extremidades pertencem à circunferência.
Diâmetro: Diâmetro de uma circunferência (ou de um
círculo) é uma corda que passa pelo centro da
circunferência. Observamos que o diâmetro é a maior
corda da circunferência.
Uma relação importante que podemos notar é que a medida do
diâmetro (d) é igual ao dobro da medida do raio (r), ou seja,
diâmetro = 2r.
Círculo (ou disco) é o conjunto de todos os pontos de um
plano cuja distância a um ponto fixo O é menor ou igual que
uma distância r dada. Quando a distância é nula, o círculo se
reduz a um ponto. O círculo é a reunião da circunferência com
o conjunto de pontos localizados dentro da mesma.
CÍRCULO
O
r
diâmetro

6. Corda: segmento que une
dois pontos quaisquer da
circunferência
Diâmetro é a maior corda.
Raio de uma circunferência (ou
de um círculo) é um segmento
de reta com uma extremidade
no centro da circunferência e a
outra extremidade num ponto
qualquer da circunferência

7. Quadrilátero
Num quadrilátero AEOU da figura, podemos destacar os seguintes elementos:
Os pontos A, E, O, U são vértices.
Os ângulos Â, Ê, Ô e Û são ângulos internos.
As segmentos AE, EO, OU, UA são lados.
Os segmentos AO e EU são diagonais.
A E
OU

8. Quadrilátero convexo e côncavo
Observe os quadriláteros abaixo:
R
S T
U
No quadrilátero ABCD, as retas AB, BC, CD
e DA não cortam nenhum lado do
quadrilátero.
ABCD é um quadrilátero convexo.
No quadrilátero RSTU, a reta TU corta o
lado RS.
RSTU é um quadrilátero côncavo.
C
D
B
A
Trapézio
s
A
D C
B
AB // CD
Os trapézios apresentam apenas um par de lados
paralelos. Quadriláteros assim são chamados de trapézios
e os lados opostos paralelos são chamados de bases do
trapézio.

9. Observe os seguintes quadriláteros:
A B
C D
M
N
Q
P
R
U
S
T
E F
H G
AB // CD
AC // BD PQ // MN
MP // QN
RS // UT
UR // TS
EF // HG
EH // FG
Todos apresentam os lados opostos paralelos e são chamados de paralelogramos.
Paralelogramos especiais
Retângulo
A B
C D
Retângulo é o paralelogramo que tem os quatro
ângulos congruentes (retos).

10. Losango
Losango ou rombo é o paralelogramo que tem os
quatro lados congruentes.
Quadrado
Quadrado é o paralelogramo que tem quatro lados congruentes
e quatro ângulos congruentes.
GEOMETRIA
Ponto

15. r p (Lê-se r é perpendicular a p)
POSIÇÃO RELATIVA DE DUAS RETAS NO
PLANO
Retas concorrentes
Duas retas de um plano são concorrentes se têm um e um
só ponto comum. Ao serem concorrentes podem ser
concorrentes perpendiculares ou concorrentes oblíquas.
Retas concorrentes perpendiculares Retas concorrentes oblíquas
As retas concorrentes perpendiculares dividem o As retas concorrentes oblíquas dividem o
plano em quatro partes geometricamente iguais. plano em quatro partes que não são
geometricamente iguais.
x
p
v
r
x v (Lê-se x é oblíqua a v)

16. u t ( Lê-se u é estritamente paralela a t )
Retas paralelas
Duas retas de um plano são paralelas se não têm nenhum
ponto em comum (estritamente paralelas) ou se têm todos
os pontos em comum (coincidentes).
As retas estritamente paralelas não têm nenhum ponto As retas coincidentes têm todos os pontos em
em comum, estão sempre à mesma distância e têm a comum. A distância entre duas retas coincidentes
mesma direção. é nula.
t
iu
i j ( Lê-se i é coincidente com j )
j

17. Retas Perpendiculares: são retas que se
encontram e formam ângulos de 90°.