Este documento apresenta os principais tópicos da matemática básica, incluindo teoria dos conjuntos, números, módulo, expressões algébricas, funções, geometria plana e trigonometria. O documento fornece definições, propriedades e exemplos para cada tópico, além de exercícios resolvidos.









![2.2.1 Propriedades das desigualdades
a) Se a > b e b > c então a > c, Ex: 10 > 0 > −10 ⇒ 10 > −10
b) Se a > b então a ± c > b ± c, Ex: 10 ± 5 > −10 ± 5 ⇒ 15 > −5 e 5 > −15
c) Se a > b e c > 0 então ac > bc, Ex: 10.5 > −10.5 ⇒ 50 > −50
d) Se a > b e c < 0 então ac < bc, Ex: 10. − 3 < −10. − 3 ⇒ −30 < 30
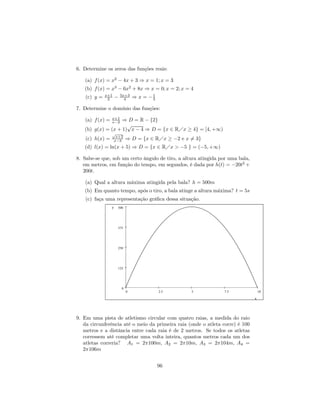
e) Se a > b então a < 1 , se a 6= 0 e b 6= 0
1
b
2.2.2 Intervalos
Sendo a e b dois números reais, com a < b, temos os seguintes subconjuntos de
R chamados intervalos.
Intervalo aberto:
(a, b) = {x ∈ R Á a < x < b}
Intervalo fechado:
[a, b] = {x ∈ R Á a ≤ x ≤ b}
Intervalo semi-aberto à direita:
[a, b) = {x ∈ R Á a ≤ x < b}
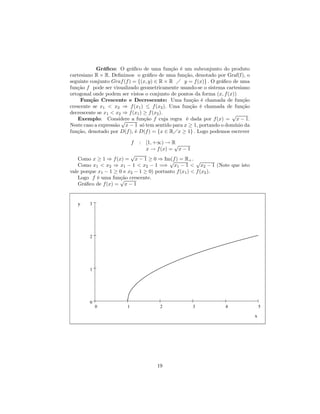
Intervalo semi-aberto à esqueda:
(a, b] = {x ∈ R Á a < x ≤ b}
Intervalo infinitos
(−∞, +∞) = {x ∈ RÁ − ∞ < x < +∞} = R
[a, +∞) = {x ∈ R Á a ≤ x < +∞}
(a, +∞) = {x ∈ R Á a < x < +∞}
9](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-10-320.jpg)
![(−∞, a] = {x ∈ R Á − ∞ < x ≤ a}
(−∞, a) = {x ∈ R Á − ∞ < x < a}
2.2.3 Exercicios Resolvidos
1) Usando a notação de conjunto escrever os intervalos
£√ √ ¤
a) (−3, 6) b) (π, 6] c) 2, 3 d) [−1, 0) e) (−∞, 0)
2) Se A = {x ∈ R Á 2 < x < 5} e B = {x ∈ RÁ3 ≤ x < 8} determinar
a) A ∩ B b) A − B c) B − A
3) Representar os seguintes intervalos:
a) [−1, 1] b) [0, 10) c) (−3, 1] d) (4, 6) e) (5, +∞)
4) Resolver graficamente £√ √ ¤ £ 1 ¤
a) (π, 6] ∪ [−1, 1) b) 2, 3 ∩ 2 , 3
5) Resolver as inequações
a) 3 + 7x ≤ 2x + 9 b) 7 ≤ 2 − 5x < 9
c) 2x−5 < 1
x−2 d) x−1 ≥ 4
x
2.3 Exercícios de Fixação
01) Quais das alternativas abaixo é falsa
a) {∅} é um conjunto unitário
b) {} é o conjunto vazio
c) Se A = {1, 2, 3} então {3} ∈ A
d) {x ∈ NÁx = 2n , onde n ∈ N} é o conjunto dos números naturais ímpares
£ ¤
e) £∅ ⊂ ¤1 , −1
2 2
f) 1 , −1 ∪ {} ⊂ ∅
2 2
h) B ∩ A ⊂ A ∪ B
i) Q ⊂ R − Z
02) Escrever usando o sinal de desigualdade
a) a é um número positivo b) b é um número negativo c) a é maior que
b
03) Representar na reta real os seguintes intervalos
a) [−10, 11] b) [0, 3) c) (−3, 0] d) (3, 7) e) (0, +∞)
04) Representar graficamente os intervalos dados pelas desigualdades
√ √
a) 2 ≤ x ≤ 7 b) 3 ≤ x ≤ 5 c) 0 ≤ x < 2 d) −∞ < x < −1
05) Deternimar graficamente
a) (5, 7] ∩ [6, 9] b) (−∞, 7] ∩ [8, 10] c) (−3, 0] ∪ (0, 8) d) (0, 7] − (5, 7)
06) Sejam M = {x ∈ RÁ2 ≤ x < 10}, N = {x ∈ R Á 3 < x < 8} e P =
{x ∈ RÁ2 ≤ x ≤ 9} . Determinar o conjunto P − (M − N ).
10](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-11-320.jpg)













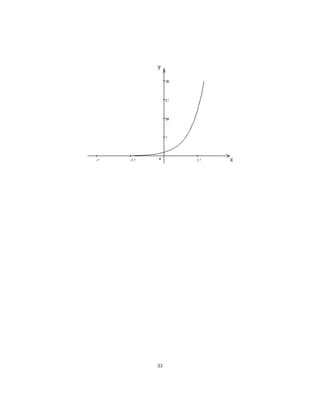

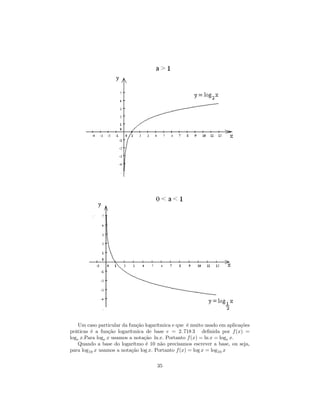
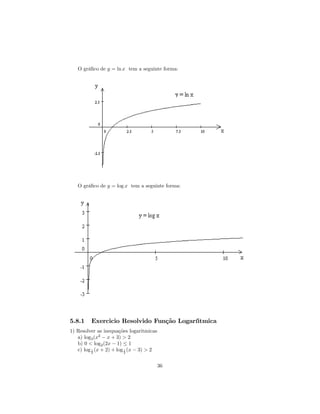
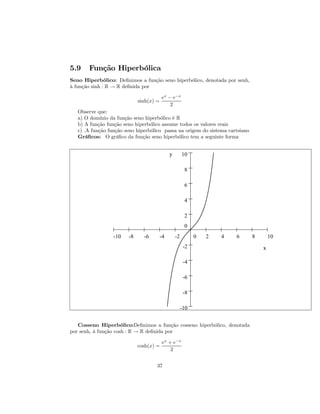



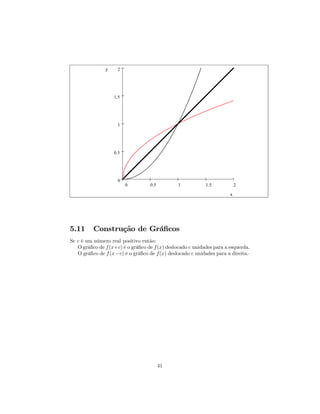
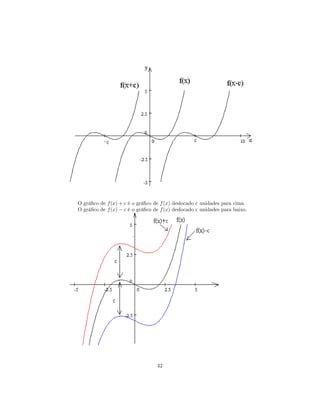
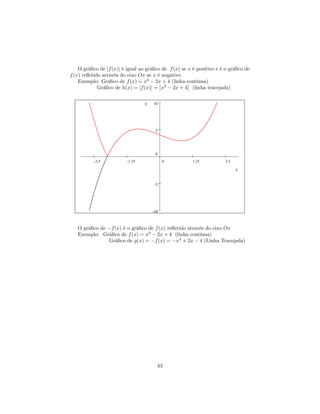
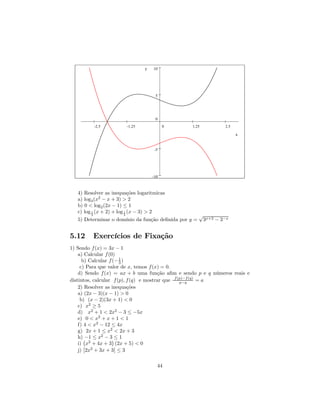

![a) y = log10 (x + 5)
b) y = − ln x
c) y = ln(−x)
d) y = ln |x|
11) Resolva cada equação em x
a) ln x = −1
b) ln(2x − 1) = 3
c) e3x−4 = 2
d) eax = Cebx , onde C é uma constante e a 6= b
ln(ln x) = 1
12) Se a população de bactérias começa com 100 e dobra a cada três horas,
t
então o número de bactérias após t horas é n = f (t) = 100.2 3 :
a) Encontre a função inversa de f e explique seu significado.
b) Quando a população atingirá 50.000 bactérias?
13) Após acionado o Flash de uma câmera, a bateria imediatamente começa
a recarregar o capacitor do flash, o qual armazena uma carga elétrica dada por
t
Q(t) = Q0 (1 − e− a ) (A capacidade máxima de carga é Q0 , e t é medido em
segundos.)
a) Encontre a função inversa de Q e explique seu significado.
b) Quanto tempo levará para o capacitor recarregar 90% da capacidade se
a = 2?
14) Se f (x) = ln x e g(x) = x2 − 9, encontre as funções f ◦ g, g ◦ f, f ◦ f, g ◦ g
15) Expresse a função F (x) = √ 1 √ como uma composta de três funções.
x+ x
1
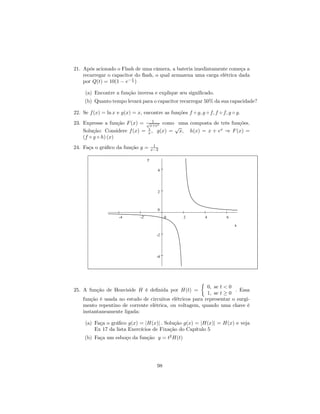
16) Faça o gráfico da função y = x ½
0, se t < 0
17) A função de Heaviside H é definida por H(t) = . Essa
1, se t ≥ 0
função é usada no estudo de circuitos elétricos para representar o surgimento
repentino de corrente elétrica, ou voltagem, quando uma chave é instantanea-
mente ligada:
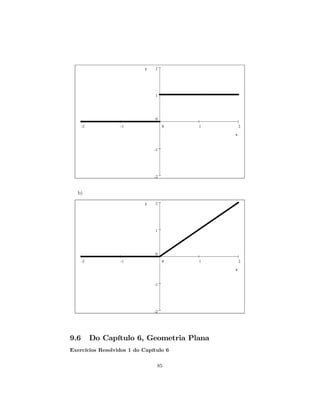
a) Faça o gráfico da função de heaviside
b) Faça um esboço da função rampa y = tH(t)
18) Seja f : R → R uma função qualquer, encontre duas funções g, h : R → R,
g(x) é uma função par e h(x) é uma função impar, tal que
f (x) = g(x) + h(x)
19) Uma função f : R → R é chamada de função convexa se f (tx+(1−t)y) ≤
tf (x) + (1 − t)f (y), ∀t ∈ [0, 1].
a) Mostre que a função f (x) = x2 é uma função convexa
b) Mostre que a função f (x) = ex é uma funação convexa
c) Mostre que a função f (x) = |x| é uma funação convexa
d) O que significa geometricamente a desigualdade f (tx+(1−t)y) ≤ tf (x)+
(1 − t)f (y), ∀t ∈ [0, 1]?
46](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-47-320.jpg)












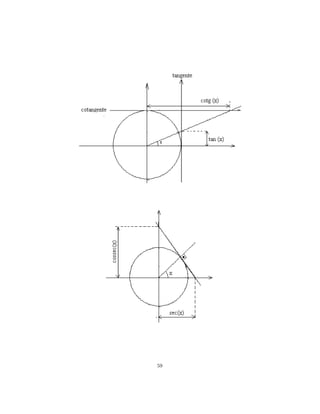
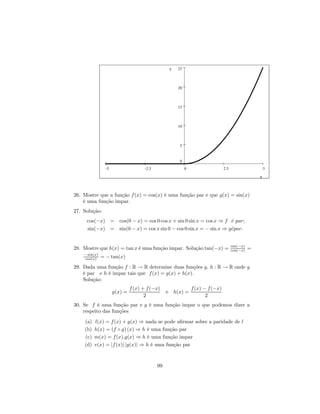
![7.6 Funções Trigonométricas
Função Seno: f : R → R, f (x) = sen(x), Dom(f ) = R, Im(f ) = [−1, 1]
Função Cosseno: f : R → R, f (x) = cos(x), Dom(f ) = R, Im(f ) =
[−1, 1]
© nπ ª
© Função tangente:f : R − 2 Án ∈ Z → R,
ª f (x) = tan(x), Dom(f ) =
x ∈ RÁx 6= nπ , n ∈ Z , Im(f ) = R
2
60](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-61-320.jpg)

![a) sin(π − θ) = sin θ. sin(π + θ) = − sin θ sin(−θ) = − sin θ.
b) cos(π − θ) = − cos θ. cos(π + θ) = − cos θ. cos(−θ) = cos θ
c) tan(π − θ) = − tan θ. tan(π + θ) = tan θ tan(−θ) = − tan θ.
d) sin θ = sin(θ + 2π) sin θ = sin(θ − 2π). sin(θ + 2π) = sin(θ − 2π)
e) cos θ = cos(θ + 2π) cos θ = cos(θ − 2π). cos(θ + 2π) = cos(θ − 2π).
f ) tan θ = tan(θ + 2π) = tan(θ − 2π) = tan(θ + π) tan θ = tan(θ − π).
g) sin θ = sin(θ ± 2nπ), n = 0, 1, 2,
h) cos θ = cos(θ ± 2nπ), n = 0, 1, 2,
i) tan θ = tan(θ ± nπ), n = 0, 1, 2, ...
Ângulos Complementares
j) sin θ = cos( π − θ)
2
k) cos θ = sin( π − θ)
2
π
cos( 2 −θ)
l) tan θ = sin( π −θ) = = cot( π − θ)
2
2
m) cot θ = tan( π − θ)
2
Fórmulas de adição e subtração:
a) sin(α + β) = sin α. cos β + sin β. cos α
b) sin(α − β) = sin α. cos β − sin β. cos α
c) cos(α + β) = cos α. cos β − sin α. sin β
d) cos(α − β) = cos α. cos β + sin α. sin β
tan α+tan β
e) tan(α + β) = 1−tan α. tan β
tan α−tan β
f) tan(α − β) = 1+tan α. tan β
→
Fórmulas de ângulo duplo:
a) sin 2Φ = 2. sin Φ. cos Φ
b) cos 2Φ = cos2 Φ − sin2 Φ
c) tan 2Φ = 1−tan2Φ
2. tan
Φ
Fórmulas do ângulo metade:
a) sin2 ϕ =
2
1−cos ϕ
2
b) cos2 ϕ =
2
1+cos ϕ
2
Formulas de produto em soma:
a) sin α. cos β = 1 [sin(α − β) + sin(α + β)]
2
b) sin α. sin β = 1 [cos(α − β) − cos(α + β)]
2
c) cos α. cos β = 1 [cos(α − β) + cos(α + β)]
2
62](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-63-320.jpg)

![Dados: P Q = 10m, T R = 2, 3m, P T = x, QS = y
10) Um carro sobe uma via em forma de plano inclindado, com inclinação
de 20◦ em relação à horizontal. Em que altura, em relação à horizontal, o carro
estará se percorrer 1 km na via. Dado: sin 20 = 0, 34
11) Se θ é um ângulo agudo, use identidades fundamentais para escrever a
primeira expressão em função da segunda:
a) cot θ; sin θ
b) sec θ; sin θ
c) tan θ; cos θ
d) csc θ; cos π
e) tan θ; sec θ
12) Fazendo a substituição trigonométrica x = a sin θ para - π ≤ θ ≤ π ,
√ 2 2
escreva a2 − x2 em termos de uma função trigonométrica de θ.
13)√ Usando a substituição indicada simplifique os radicais:
a) 16 − x2 ; x = 4 sin θ para - π ≤ θ ≤ π
2 2
x2
b) √9−x2 ; x = 3 sin θ para - π ≤ θ ≤ π
2 2
c) √25+x2 ; x = 5 tan θ para - π ≤ θ ≤ π
x
2 2
√
2
d) x 2+4 ; x = 2 tan θ para - π ≤ θ ≤ π
√ x 2 2
2
e) xx−9 ; x = 3 sec θ para 0 ≤ θ ≤ π 2
14) Determine os intervalos de crescimento e decrescimento para a função
f (x) = cos x definida para x ∈ [0, 2π]
15) 1+sin2 + 1+cos2 x + 1+sec2 x + 1+cos1sec2 x é igual a:
1 1 1
16) Os valores que m pode assumir para que exista um arco x satisfazendo
a igualdade sin x = m − 4 são:
17) A expressão cos2 x + cos2 x tan2 x + tan2 x é igual a:
18) Determine as soluções das equações em [0, 2π)
a) 2 sin2 u = 1 − sin u
b) cos λ − sin λ = 1
c) 2 tan − sec2 = 0
d) sin x + cos x cot x = csc x
e) sin 2t + sin t = 0
f) cos µ + cos 2µ = 0
64](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-65-320.jpg)

![Capítulo 8
Revisão Geral
Lista de Exercícios de Matemática Básica
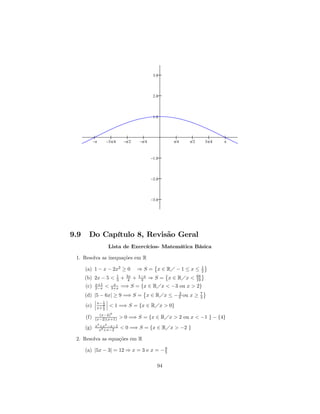
1. Resolva as inequações em R
(a) 1 − x − 2x2 ≥ 0
1 3x 1−x
(b) 2x − 5 < 3 + 4 + 3
x+1 x
(c) 2−x < 3+x
(d) |5 − 6x| ≥ 9
¯ 1¯
¯ x− 2 ¯
(e) ¯ x+ 1 ¯ < 1
2
(x−4)6
(f) (x−2)(x+1) >0
3 2
x +x −x−1
(g) x2 +x−2 <0
2. Resolva as equações em R
(a) |5x − 3| = 12
(b) (x − 3)(x + 1)(x + 4) = 0
¯ ¯
¯ 3x+8 ¯
(c) ¯ 2x−3 ¯ = 4
(d) 2x − 7 = |x| + 1
3. Dados os conjuntos: A = {x ∈ R | −10 < x < 8}, B = (−3, 5] e
C = {x ∈ R | x ≥ 2} determine:
(a) A ∪ B ∪ C
(b) B ∩ (A ∪ C)
(c) A ∪ (B ∩ C)
(d) A − B
66](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-67-320.jpg)




![9.2 Do Capítulo 2, Números
Exercicios Resolvidos do Capítulo 2
1) Usando a notação de conjunto escrever os intervalos
© ª
a) (−3, 6) ⇒ S = x ∈ RÁx ≤ −11 4
b)£√ √ ¤ ⇒ S = {x ∈ RÁπ √ x ≤ 6} √ ª
(π, 6] © <
c) 2, 3 ⇒ S = x ∈ RÁ 2 ≤ x ≤ 3
d) [−1, 0) ⇒ S = {x ∈ RÁ − 1 ≤ x < 0}
e) (−∞, 0) ⇒ S = {x ∈ RÁ − ∞ < x < 0}
2) Se A = {x ∈ R Á 2 < x < 5} e B = {x ∈ RÁ3 ≤ x < 8} determinar
a) A ∩ B = {x ∈ R Á 3 ≤ x < 5}
b) A − B = {x ∈ R Á 2 < x < 3}
c) B − A = {x ∈ R Á 5 ≤ x < 8}
3) Representar os seguintes intervalos:
a) [−1, 1] b) [0, 10) c) (−3, 1] d) (4, 6) e) (5, +∞)
4) Resolver graficamente £√ √ ¤ £ 1 ¤
a) (π, 6] ∪ [−1, 1) b) 2, 3 ∩ 2 , 3
5) Resolver as inequações © ª
a) 3 + 7x ≤ 2x + 9 ⇒ S =© x ∈ RÁx ≤ 6 5 ª
b) 7 ≤ 2 − 5x < 9 ⇒ S = x ∈ RÁ −7 < x ≤ −15
c) 2x−5 < 1 ⇒ S = {x ∈ RÁ2 < x < 3}
x−2 £ ¢
d) x−1 ≥ 4 =⇒ S = −1 , 0
x 3
Exercicios de Fixação do Capítulo 2
01) Quais das alternativas abaixo é falsa
a) {∅} é um conjunto unitário ⇒ F
b) {} é o conjunto vazio ⇒ F
c) Se A = {1, 2, 3} então {3} ∈ A ⇒ F
d) {x ∈ NÁx = 2n , onde n ∈ N} ⊂ Z − {x ∈ NÁx = ±2n + 1, onde n ∈ N}
⇒V £1 ¤
e) £∅ ∈ ¤ , −1 ⇒ F
2 2
f) 1 , −1 ∪ {} ⊂ ∅ ⇒ F
2 2
h) B ∩ (A − B) = ∅ ⇒ V
i) Q ⊂ R − Z ⇒ F
02) Escrever usando o sinal de desigualdade
a) a é um número positivo ⇒ a > 0
b) b é um número negativo ⇒ b < 0
c) a é maior que b ⇒ a > b
03) Representar na reta real os seguintes intervalos
a) [−10, 11] b) [0, 3) c) (−3, 0] d) (3, 7) e) (0, +∞)
04) Representar graficamente os intervalos dados pelas desigualdades
√ √
a) 2 ≤ x ≤ 7 b) 3 ≤ x ≤ 5 c) 0 ≤ x < 2 d) −∞ < x < −1
05) Deternimar graficamente
a) (5, 7] ∩ [6, 9] b) (−∞, 7] ∩ [8, 10] c) (−3, 0] ∪ (0, 8) d) (0, 7] − (5, 7)
71](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-72-320.jpg)
![06) Sejam M = {x ∈ RÁ2 ≤ x < 10}, N = {x ∈ R Á 3 < x < 8} e P =
{x ∈ RÁ2 ≤ x ≤ 9} . Determinar o conjunto P − (M − N ).
Solução: P − (M − N ) = (3, 8)
07) Resolva as inequações e exprima a solução em termos de intervalos
quando possível:
a) 2x + 5 < 3x − 7 ⇒ S = ¡(12, +∞)¢
b) x − 8 < 5x + 3 ⇒ S = −11 , ∞
4
c) −2 ≤ 2x−3 < 7 ⇒ S = [ −7 , 19)
5 2
d) 2x−3 > 2 ⇒ S = ( 3 , 7 )
x+1
2 3
9.3 Do Capítulo 3, Módulo
Exercícios resolvidos do Capítulo 3
1) Completar as implicações abaixo
a) Se |x| = 5 então x = 5 ou x = −5
b) Se |x| = 0 então x = 0
c) Se |x| < 3 então −3 < x < 3
d) Se |x| > 7 então x > 7 ou x < −7
2) Representar na reta real os pontos que satisfazem as seguintes relações
a) |x| = 3 b) |x| < 3 c) |x| > 1 |x − 3| = 5
3) Resolver
a) |x − 3| < 4 ⇒ S = (−1, 7)© ª ©
¡ ¢ ª
b) |2x−3| > 5 ⇒ S = 7 , 8 − 3 = x ∈ RÁ 7 < x < 8 e x 6= 3
1
5 ©
5 2 5 ª 5 2
c) |3x − 4| > 2 ⇒ S = x ∈ RÁx < 2 ou x > 2
3
d) |3x − 2| = |5x + 4| ⇒ x = −3 ou x = − 1 4
e) |x + 4| ≥ 2 ⇒ S = (−∞, −6] ∪ [−2, +∞)
Exercícios de Fixação do Capítulo 3
1) Reescreva sem usar o símbolo de valor absoluto
a) (−5) |3 − 6| = −15
b) |−6| = 3
2
c) |−7| + |4| = 11
d) |4 − π| = 4 − π
2) Use a definição de módulo para reescrever sem usar o símbolo de módulo
a) se x < −3 então |x + 3| = −x − 3
b) se x > 5 então |5 − x| = x − 5
3) Resolver as equações em R
a) |5x − 3| = 12 ⇒ x = 3; x = − 9 5
b) ¯ − 3| = |7x − 5| ⇒ x = 2 ; x = 8
|2x ¯ 5 9
¯ x+2 ¯ 4
c) ¯ x−2 ¯ = 5 ⇒ x = 3; x = 3
d) |3x + 2| = 5 − x ⇒ x = 3 ; x = − 7
4 2
e) 2x − 7 = |x| + 1 ⇒ x = 8
4) Resolva a desigualdade e exprima a solução em termos de intervalos,
quando possível
a) |x + 3| < 0, 01 ⇒ S = (−3.01, −2.99)
72](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-73-320.jpg)
![¡ ¢
b) |2x + 5| < 4 ⇒ S = ¡ 9 , − 1
−2 2 ¢
c) |3x − 7| ≥ 5 ⇒ S = −∞, 2 ] ∪ [4, +∞
¡ 3 ¢
d) |−11 − 7x| > 6 ⇒ S = −∞, − 17 ) ∪ [− 5 , +∞
7 7
e) 3 ≤ |x − 2| ≤ 7 ⇒ S = [−5, −1] ∪ [5, 9]
2
f) |x+3| < 1 ⇒ S = (−∞, −5) ∪ (−1, +∞)
g) |x + 4| ≤ |2x − 6| ⇒ S = (−∞, 2 ] ∪ [10, +∞)
¯ ¯ 3
¯ ¯ £ ¤
h) ¯ 7−2x ¯ ≤ 1 ⇒ S = 9 , 19
5+3x 2 7
i) |x − 1| + |x + 2| ≥ 4 ⇒ S = (−∞, − 5 ) ∪ ( 3 , +∞)
¯ ¯ ¯ ¯ 2 2
¯ 5 ¯ ¯ 1 ¯ © ª
j) ¯ 2x−1 ¯ ≥ ¯ x−2 ¯ ⇒ S = (−∞, 11 ) ∪ (3, +∞) − 1
7 2
1 1
k) |x+1||x−3| ≥ 5 ⇒ S = [−2, 4] − {−1, 3}
9.4 Do Capítulo 4, Expressões Algébricas
Exercicios Resolvidos 1 do Capítulo 4
1) 10m + 10n = 10(m + n)
2) 6xy 5 + 12x2 y 2 = 6xy 2 (2x + y 3 )
3) 4bx − 32b + 4by = 4b(x + y − 8)
4) 4x + 4z − bx − bz ¡ 4(x + z) − b(x + z)
= ¢
5) x + x2 + x3 + 1 = x2 + 1 (x + 1)
Exercicios Resolvidos 2 do Capítulo 4
1) Reescreva usando produtos notáveis:
a) (a + 2)(a − 2) = a2 − 4
b) (xy + 3z)(xy − 3z) = x2 y 2 − 9z 2
c) (x2 − 4y)(x2 + 4y) = x4 − 16y 2
e) (x + 3)2 = 6x + x2 + 9
f) (2a − 5)2 = 4a2 − 20a + 25
g) (2xy + 4)2 = 16xy + 4x2 y 2 + 16
i) (x + 4)3 = x3 + 12x2 + 48x + 64
j) (2a + b)3 = 8a3 + b3 + 6ab2 + 12a2 b
l) (a − 1)3 = 3a − 3a2 + a3 − 1
m) Calcule 41.39 usando um produto notável: (40 + 1)(40 − 1) = 402 − 12 =
1.599
n) Calcule 101.99 usando um produto notável: (100 + 1) (100 − 1) = 1002 −
1 = 9999.
Exercícios de Fixação do Capítulo 4
1 ) A soma de dois números é igual a 10 e a soma dos seus cubos é igual a
100. Qual o valor do produto desses números?
Sugestão Expandir (a+b)3 . Efetuar a multiplicação de ab (a + b) . Comparar
os dois resultados e usar os dados do problema para calcular o valor de ab.
Solução: ab = 30
73](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-74-320.jpg)


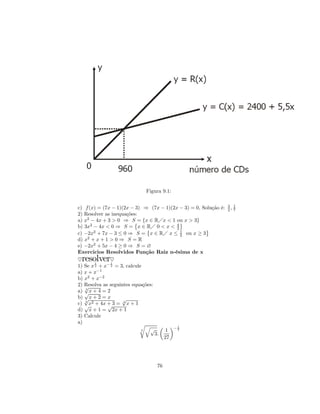

![x 2
d) x−1 − x+1 ≤ 0 ⇒ S = {x ∈ RÁ − 1 < x < 1}
x−1 x−3
e) x−2 < x−4 ⇒ S = {x ∈ RÁx < ¡ ou x > 4}
2
2
¢
f) ≥ x−5 ⇒ S = (−∞, −8] ∪ − 3 , 5
2
2x+3
x−2
¡ 5 2 ¢
g) 3x+5 ≤ 4 ⇒ S = (−∞, −2] ∪ − 3 , +∞
x+1
¡3 7¢
h) 2x−3 > 2 ⇒ S = 2 , 3
x+1 x
i) 2−x < 3+x ⇒ S = (−∞, −3) ∪ (2, +∞)
4) Resolver as equações exponenciais
a) 2x−3 + 2x−1 + 2x = 52 ⇒ x = 5
³√ ´x−2
3
b) 2x+4 = 1 ⇒ x = −4 e x = 2
5) Resolver as inequações exponenciais
¡√ ¢2x+4 ¡√ ¢3x
a) 3 > 3 ⇒ S = (−∞, 4)
2
b) 5x −8x−20 < 1 ⇒ S = (−2, 10)
2 © ª
c) (0, 3)4x −2x−2 ≥ (0, 3)2x−3 ⇒ S = 1 2
6) Resolver as inequações logarítmicas
a) log2 (x − 2) − log 1 (x − 3) < 1 =⇒ S = {x ∈ RÁ3 < x < 4}
2 n √ q q √ o
b) log 1 (x2 − 3 ) ≥ 1 =⇒ S = x ∈ RÁ − 2 ≤ x < − 3 ou 3 < x < 2
2 2 2
2
n √ √ o
c) x(loga x)+1 > a2 x para 0 < a < 1 =⇒ S = x ∈ RÁa− 2 < x < a 2
p
d) Dar o domínio da função f (x) = √ log(x2 − 2x) √ ª
©
Solução: D (f ) = x ∈ RÁx ≤ 1 − 2 ou x ≥ 1 + 2
7) Se uma bola é atirada para cima com uma velocidade inicial de 32 m/s,
então, após t segundos, a distância s acima do ponto de partida, em metros, é
dada por s = 32t − 16t2 . Em que instante a bola estará no ponto mais alto e
qual será esta altura? Faça um esboço do gráfico da equação. Solução t = 1s
e s = 16m
8) A energia potencial elástica W armazenada numa mola esticada é dada
pela expressão W = 1 kx2 onde k é a constante elástica da mola e x é o quanto
2
a mola está alongada
Para uma constante elástica igual a 10 unidades
a) Qual o número que exprime o valor de sua energia potencial W , para um
alongamento de 2 unidades
b) De quanto está esticada a mola quando sua energia potencial é de 80
unidades
Solução a) W = 20 b) x = 4 unidades.
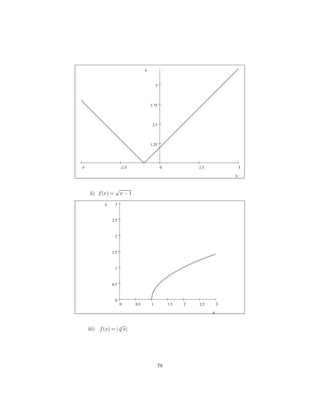
9) Desenhar o gráfico das seguintes funções
i) f (x) = |x + 1|
78](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-79-320.jpg)
![y
2.5
1.25
0
-2.5 -1.25 0 1.25 2.5
x
-1.25
-2.5
¯ ¯
iv) f (x) = ¯x2 + x − 6¯
y 15
12.5
10
7.5
5
2.5
-5 -2.5 0 2.5 5
x
10) Especifique o domínio e faça um esboço do gráfico de cada uma das
funções:
a) y = log10 (x + 5) ⇒ Dom(y) = {x ∈ RÁx > −5} = (−5, +∞]
80](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-81-320.jpg)
![y 5
2.5
0
-5 -2.5 0 2.5 5
x
-2.5
-5
b) y = − ln x ⇒ Dom(y) = {x ∈ RÁx > 0} = (0, +∞]
y
4
2
0
0 2 4
x
-2
c) y = ln(−x) ⇒ Dom(y) = {x ∈ RÁx < 0} = (−∞, 0)
y = ln(−x)
81](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-82-320.jpg)
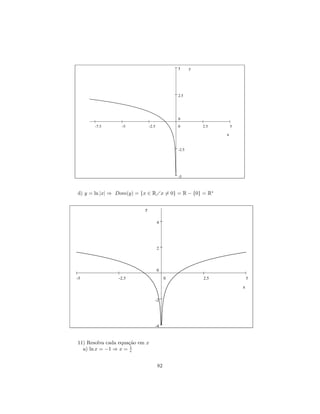






![12) Fazendo a substituição trigonométrica x = a sin θ para - π ≤ θ ≤
π
√ 2
2 , escreva a2 − x2 em termos de uma função trigonométrica de θ. Solução:
√
a2 − x2 = a cos θ
13) Usando a substituição indicada simplifique os radicais:
Solução: Em caso de dúvida chame o professor
14) Determine os intervalos de crescimento e decrescimento para a função
f (x) = cos x definida para x ∈ [0, 2π]
15) 1+sin2 x + 1+cos2 x + 1+sec2 x + 1+cos1sec2 x é igual a: 2
1 1 1
16) Os valores que m pode assumir para que exista um arco x satisfazendo
a igualdade sin x = m − 4 são: 3 ≤ m ≤ 5
17) A expressão cos2 x + cos2 x tan2 x + tan2 x é igual a: sec2 x
18) Determine as soluções das equações em [0, 2π)
a) 2 sin2 u = 1 − sin u ⇒ u = π , 5π , 3π
6 6 2
b) cos λ − sin λ = 1 ⇒ λ = 0, 3π 2
c) 2 tan − sec2 = 0 ⇒ = π , 5π 4 4
d) sin x + cos x cot x = csc x ⇒ x ∈ R
e) sin 2t + sin t = 0 =⇒ t = 0, 2π , π, 4π
3 3
f) cos µ + cos 2µ = 0 =⇒ µ = π, π , 5π
3 3
g) tan 2x = tan x =⇒ x = 0 e x = π
h) sin u + cos u = 1 =⇒ u = 0, π , 5π .
2 3 3
19) Sugestão: Use a lei dos cossenos ou calcule diretamente usando relações
trigonométricas
20) Desenhe o gráfico das seguintes funções:
a) y = sin(3x)
90](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-91-320.jpg)
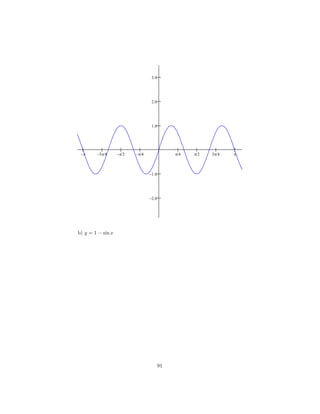
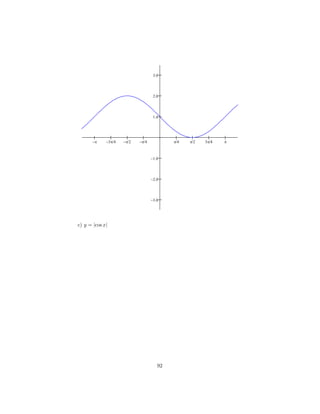
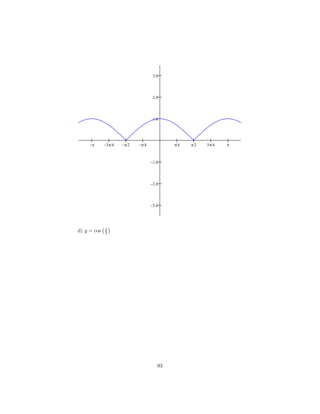
![(b) (x − 3)(x + 1)(x + 4) = 0 ⇒ x = 3 , x = −1 e x = −4
¯ ¯
¯ 3x+8 ¯ 4
(c) ¯ 2x−3 ¯ = 4 ⇒ x = 4 e x = 11
(d) 2x − 7 = |x| + 1 ⇒ x = 8
3. Dados os conjuntos: A = {x ∈ R | −10 < x < 8}, B = (−3, 5] e
C = {x ∈ R | x ≥ 2} determine:
(a) A ∪ B ∪ C = (−10, +∞)
(b) B ∩ (A ∪ C) = (−3, 5]
(c) A ∪ (B ∩ C) = (−10, 8)
(d) A − B = (−10, −3] ∪ (5, 8)
(e) C − (A ∩ C) = [8, +∞)
4. O consumo C de água em m3 , pela população de uma cidade em função
do tempo t, em segundos, é dado pela equação C = 2000t.
(a) Qual o consumo de água dessa população em 10 segundos? C = 2.104
m3
(b) Qual é o consumo de água dessa população em 10 horas? C = 72.106
m3
(c) Em quantos segundos essa população consome 48.000m3 de água?
t = 24s
5. Dada a função f (x) = 3x + 4 determine:
(a) f (−1) = 1
(b) o valor de x tal que f (x) = 10 ⇒ x = 2
(c) Faça a representação gráfica dessa função
y
15
10
5
0
-5 -2.5 0 2.5 5
x
-5
-10
95](https://image.slidesharecdn.com/apostila8-111128063447-phpapp02/85/Apostila8-96-320.jpg)