1) O documento apresenta um roteiro geral de ensino fundamental que inclui tópicos de matemática elementar como números naturais, inteiros, racionais, frações, equações de 1o grau, razões e proporções. 2) É fornecido um mini dicionário de termos matemáticos que aparecem nos tópicos como ábaco, adição, algoritmo, ângulo, área, entre outros. 3) Os tópicos vão desde a origem dos números e sistema de numeração até equações do 2o gra

1. Ensino Fundamental Roteiro geral
1. Dicionário de Matemática Elementar
Pequeno dicionário de Matemática Elementar.
2. Origem dos números
O surgimento do processo de numeração. Representação numérica. A capacidade humana de
quantificar objetos. O ábaco. O sistema de numeração indo-arábico. Notação posicional e a criação do
zero. O sistema de numeração. Observações sobre a numeração egípcia. O sistema de numeração
romana.
3. Números naturais (primeira parte)
Introdução, construção, igualdade, desigualdades e operações com números naturais.
4. Números naturais (segunda parte)
Múltiplos e Divisores naturais. Números primos. Crivo de Eratóstenes. Mínimo Múltiplo Comum (MMC)
e o algoritmo para a sua obtenção. Máximo Divisor Comum (MDC) e o algoritmo para a sua obtenção.
Relação entre MMC e MDC. Primos entre sí. Radiciação.
5. Critérios de divisibilidade
Lista ímpar de Critérios de divisibilidade por: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 17, 19, 23, 29, 31 e 49.
Certamente você não encontrará este material em livros comuns! Em todos os casos há exemplos
para você praticar.
6. Exercícios sobre mmc, mdc e divisibilidade
Exercícios Resolvidos sobre Números Naturais, Múltiplos e Divisores naturais.
7. Números inteiros
Curiosidades com números inteiros. Introdução aos números inteiros. Sobre a origem dos sinais. O
conjunto Z dos Números Inteiros. A Reta Numerada. Ordem e simetria no conjunto Z. Módulo de um
número Inteiro. A soma de números inteiros e suas propriedades. A Multiplicação de números inteiros
e suas propriedades. A propriedade distributiva. Potenciação e radiciação de números inteiros.
8. Frações
O papel das frações e números Decimais. Elementos históricos sobre os números Decimais. Frações e
números Decimais. Leitura de Números Decimais. Transformação de frações decimais em números
decimais. Transformação de números decimais em frações decimais. Propriedades dos números
decimais. Operações com números decimais. Expressões com números decimais. Comparação de
números decimais. Porcentagem.
9. Frações decimais
Frações: elementos históricos, conceito, construção, definição, leitura, tipos e a propriedade
fundamental. A fração como classe de equivalência. Números mistos. Simplificação de frações.
Representação gráfica.
10. Números racionais
Relação entre números racionais e frações. Dízima periódica. A Conexão entre números racionais e
números reais. Geratriz de uma dízima periódica. Números irracionais. Representação geométrica dos
racionais. Ordem e simetria no conjunto Q. Módulo de um número racional. Adição e propriedades dos
números racionais. Produto e propriedades dos números racionais. Propriedade distributiva em Q.
Potenciação de números racionais. Radiciação de números racionais. Médias: Aritmética, Aritmética
Ponderada, Geométrica e Harmônica.
11. Exercícios sobre frações e números decimais
Exercícios resolvidos de frações decimais e números Decimais.
12. Equações do 1o. grau

2. Introdução as equações e sentenças matemáticas. Equações do primeiro grau (1 variável).
Desigualdades do primeiro grau (1 variável). Desigualdades do primeiro grau (2 variáveis). Sistemas de
equações primeiro grau. Desigualdades com duas equações.
13. Razões e proporções
Razões. Proporções. Propriedade fundamental das proporções. Razões e Proporções de Segmentos.
Polígonos e Figuras Semelhantes. Aplicações práticas das razões.
14. Aplicações das Razões e proporções
Proporções com números e propriedades. Grandezas direta e inversamente proporcionais. Elementos
históricos sobre a Regra de três. Regras de três simples direta e inversa. Regras de três composta.
Porcentagem. Juros simples.
15. Divisão proporcional
Decomposição de um número em n partes: diretamente proporcionais, inversamente proporcionais,
simultaneamente em n partes direta e inversamente proporcionais. Regras de Sociedade.
16. Expressões algébricas
Expressões Numéricas e a sua importância. Elementos históricos. Expressões algébricas. Prioridade
das operações numa expressão algébrica. Monômios e polinômios. Valor numérico de uma expressão
algébrica. A regra dos sinais (multiplicação ou divisão). Regras de potenciação. Eliminação de
parênteses em Monômios. Operações com expressões algébricas de Monômios. Alguns Produtos
notáveis.
17. Equações do 2o.grau
Equações do segundo grau. A fórmula de Sridara (conhecida como sendo de Bhaskara). Exercícios e
algumas tabelas interessantes.
18. Funções quadráticas
A função quadrática ou trinômia do segundo grau. Quatro importantes aplicações das parábolas nem
sempre encontradas em livros básicos de Matemática até mesmo porque tais aplicações envolvem
conhecimento de assuntos tratados num curso superior.
1- Ensino Fundamental: Mini Dicionário de Matemática Elementar
A B C D E F G H I L M N O P Q R S T V
ábaco Uma calculadora com várias hastes de metal, sustentando
bolinhas que podem ser manipuladas, servindo para realizar
operações matemáticas.
abscissa Ver coordenadas
adição Uma das quatro operações básicas da aritmética, utilizada
para adicionar um número a outro.
3+2=(1+1+1)+(1+1)=(1+1+1+1+1)=5
algarismo Símbolo utilizado para escrever os números. Em nosso
sistema de numeração de base 10, existem dez algarismos:

3. 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9
algoritmo Um conjunto de regras necessárias à resolução de um
problema ou cálculo. Consideremos o problema: Sobre o conjunto
dos números reais, resolver a equação a.x+b=0, sendo a constante
a diferente de zero. Para resolver este problema, podemos utilizar o:
Algoritmo
1. Escrever a equação a.x+b=0.
2. Somar o oposto de b, que é -b a ambos os membros da
igualdade.
3. Usar o fato que b+(-b)=0, sendo que 0 é o elemento neutro da
adição de números reais.
4. Verificar que: ax=-b.
5. Multiplicar ambos os membros da nova igualdade por a-1 que é
o inverso multiplicativo de a que está garantido porque a é
não nulo.
6. Usar o fato que a.a-1=1, sendo que 1 é o elemento neutro da
multiplicação de números reais.
7. Obter a solução x=a-1.b.
amostra Um conjunto escolhido para representar uma coleção ou
população.
ângulo Ângulo é a reunião de dois segmentos de reta orientados (ou
duas semi-retas orientadas) a partir de um ponto comum. A
interseção entre os dois segmentos (ou semi-retas) é denominada
vértice do ângulo e os lados do ângulo são os dois segmentos (ou
semi-retas).

4. ângulo agudo Um ângulo que mede menos do que 90 graus e mais
do que 0 graus.
ângulo obtuso Um ângulo que mede mais do que 90 graus e menos
do que 180 graus.
ângulo raso Um ângulo que mede exatamente 180 graus.
ângulo reto Um ângulo que mede exatamente 90 graus ou um
ângulo formado pela interseção de duas retas perpendiculares.
arco de curva Parte de uma curva situada entre dois pontos
quaisquer da curva. Se A e B são dois pontos quaisquer de uma
circunferência , existem dois arcos AB, estes arcos são de
comprimentos diferentes se A e B não são pontos extremos do
diâmetro, o maior é designado arco maior e o outro, arco menor.
área É a medida de uma superfície, muitas vezes mal denominada
também como superfície.
aresta A interseção de duas faces de um sólido. No desenho em
anexo, é o segmento de reta que representa a interseção de duas
faces coloridas.

5. aritmética É o ramo da Matemática dedicado ao estudo das regras
de cálculo com números.
arredondar Fazer uma aproximação do valor de um número.
3,14 é um arredondamento de Pi=3,14159...
associativa Lei que permite reagrupar os termos de uma adição ou
multiplicação sem alterar o resultado.
(A+B)+C = A+(B+C)
(A×B)×C = A×(B×C)
A multiplicação é associativa:
a×(b×c) = (a×b)×c
2×(3×5) = (2×3)×5 =30
A adição é associativa:
a+(b+c) = (a+b)+c
2+(3+5) = (2+3)+5 =10
atributo Uma qualidade ou característica de um objeto matemático.
baricentro de um triângulo As três medianas de um triângulo se
encontram num mesmo ponto, o baricentro, este ponto divide cada
mediana em duas partes tais que, a parte que contém o vértice é o
dobro da outra. Uma lamina triângular com densidade uniforme tem
este ponto como centro de massa.

6. base de um triângulo É conveniente considerar um dos lados do
triângulo como sendo sua base, a distância entre a base e o vértice
oposto a base é a altura do triângulo.
bilhão 109=1000000000. Número 1 seguido de 9 zeros.
bissetriz É a semi-reta que divide um ângulo em dois ângulos
congruentes. Na figura a semi-reta OM é a bissetriz do ângulo AÔB
pois os ângulos AÔM e MÔB são congruentes.
biunívoca Correspondência de cada objeto a um único objeto. Por
exemplo, uma pessoa para cada carteira de identidade.
blocos lógicos Blocos utilizados em atividades didáticas de
classificação e seriação gráfica. Tais objetos normalmente são
coloridos e têm formas distintas.
calcular Realizar uma operação, como por exemplo, a adição, a
subtração, a multiplicação, a divisão ou potenciação, visando obter
um resultado.
capacidade É a quantidade que um recipiente pode conter, esta
quantidade pode ser de óleo, água, etc. Normalmente a capacidade
é medida em litros.
cilindro Uma região bidimensional no espaço tridimensional formada
por uma superfície curva e por duas superfícies planas que são
congruentes. Um cilindro circular reto pode ser visto no cotidiano
como uma lata de óleo ou de ervilha.

7. círculo Uma figura plana formada pelo conjunto de todos os pontos
deste plano situados a uma distância menor ou igual que uma
medida conhecida como raio do círculo, a partir de um ponto fixo
denominado centro do círculo.
circunferência Uma curva plana formada pelo conjunto de todos os
pontos deste plano situados a uma distância exatamente igual a
uma medida conhecida como raio da circunferência, a partir de um
ponto fixo denominado centro da circunferência. É a linha que
envolve o círculo.
classificação Forma de separar objetos ou números que possuem
certos atributos ou características.
colinear Um número qualquer de pontos são colineares se todos
estiverem sobre uma mesma reta.
compensação Um modo de realizar uma estimativa onde se pode
ajustar um resultado subestimado (abaixo do valor) ou
superestimado (acima do valor), para chegar a um resultado
aproximado mais próximo da realidade.
comutativa Lei que permite mudar a ordem dos termos de uma
adição ou multiplicação sem alterar o resultado.
A+B = B+A
A×B = B×A

8. A multiplicação é comutativa:
a×b = b×a
5×2 = 2×5 = 10
A adição é comutativa:
a+b = b+a
5+2 = 2+5 = 7
concêntrico Figuras concêntricas são aquelas que possuem o
mesmo centro.
cone Uma figura espacial tendo (em geral) uma base circular
delimitada por uma superfície curva obtida pela rotação de uma reta
em torno de um eixo fixo, sendo que estas duas retas cruzam-se no
vértice do cone.
congruência Característica do que é congruente.
congruente Figuras congruentes são aquelas que têm a mesma
forma e a mesma medida.
consecutivo Números consecutivos são números que se seguem.
Por exemplo, 3, 4, 5 e 6 são números consecutivos.
contar Associar objetos de uma forma unívoca aos números
naturais.
coordenadas As coordenadas de um ponto no plano são
identificadas por um par ordenado P=(x,y) de números, que servem
para determinar a posição deste ponto em relação ao sistema

9. considerado de eixos. A primeira coordenada×do par ordenado é a
abscissa e a segunda coordenada y é a ordenada.
As coordenadas de um ponto no espaço são identificadas por um
terno ordenado P=(x,y,z) de números que servem para determinar a
posição do ponto no espaço em relação ao sistema considerado de
eixos. A primeira coordenada×de um terno ordenado é a abscissa, a
segunda y é o afastamento e a terceira z é a cota.
corda Dois pontos A e B pertencentes a uma curva definem um
segmento de reta AB denominado corda.
criptograma Um jogo no qual os algarismos são trocados por letras
ou outros símbolos de uma operação aritmética.
cubo Um prisma retangular que tem as seis faces quadradas. Cada
conjunto de três arestas se encontra num ponto denominado vértice
e duas destas arestas sempre formam um ângulo reto. As seis faces
são paralelas duas a duas.
dados Elementos numéricos ou algébricos de informação de um
problema.
decágono Um polígono com 10 lados.

10. denominador Na fração é o número que fica em baixo. É o número
que indica em quantas partes iguais será dividido o número de cima.
ue
Na fração 3/4 o denominador é o número 4.
desigualdade Desigualdade é uma expressão em uma das formas:
a b, a<b, a<b, a>b, a b, onde a e b são quantidades ou
b, a>b,
expressões. Em desigualdades são usados os seguintes símbolos:
são
não é igual (diferente), < é menor do que, < é menor ou igual a, >
é maior do que e > é maior ou igual a.
diagonal Segmento de reta que liga dois vértices não consecutivos
de um polígono.
diâmetro No círculo, é a medida do segmento de reta que passa
do
pelo centro e que une dois pontos da circunferência do círculo.
diferença O resultado de uma subtração.
2 é a diferença entre 5 e 3, porque 2=5-3.
2=5

11. 5-3=(1+1+1+1+1)-(1+1+1)=(1+1)=2
dígitos Símbolos usados para escrever números em representação
decimal ou alguma outra base. Em notação decimal os dígitos
usados são 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Em notação binária são
usados apenas dois dígitos 0 e 1.
distributiva Lei que permite distribuir uma adição ou subtração em
relação ao produto, sem alterar o resultado.
a×(b+c) = (a×b)+(a×c)
a×(b-c) = (a×b)-(a×c)
A multiplicação é distributiva sob a adição:
5×(10+2) = (5×10)+(5×2)
A multiplicação é distributiva sob a subtração:
5×(10-1) = (5×10)-(5×1)
dividendo O número que será dividido em uma operação de divisão.
Na operação 18÷9=2, 18 é o dividendo.
divisão Uma das quatro operações básicas da aritmética. Usada
para saber o número de vezes que um número está contido em
outro número.
6÷3 = (2+2+2)÷3 = 2
divisor É o segundo termo da divisão. É o que divide o dividendo.
Na operação 18÷9=2, 9 é o divisor.
dodecaedro Um poliedro com 12 faces.
dodecágono Um polí com com 12 lados.

12. eixo de simetria A reta que separa uma figura de sua reflexão ou
rebatimento.
elemento Um objeto de um conjunto é um elemento deste conjunto.
eneágono Um polígono com 9 lados.
enumerar Associar objetos de uma forma unívoca aos números
naturais.
esfera Uma figura formada pelo conjunto de todos os pontos do
espaço tridimensional, equidistantes de um ponto fixo denominado
centro da esfera, por uma distância fixa conhecida como o raio da
esfera.
estimativa Atitude de estimar um resultado numérico. É o resultado
aproximado de uma operação. Pode ser feito mentalmente ou por
escrito. Embora saibamos que Pi=3,1415926535..., podemos fazer
uma estimativa para o valor de Pi como sendo a divisão de 22 por 7.
expressão numérica Uma expressão matemática que pode também
conter termos não matemáticos.
faces São os polígonos que delimitam um sólido.

13. fator Os números inteiros multiplicados em uma multiplicação são os
fatores. Na equação 2×6 = 12, 2 e 6 são os fatores de 12.
figura geométrica Um desenho serve para representar diversas
noções matemáticas. Uma figura geométrica pode ter dimensão: 0,
1, 2, 3, ...,n. Por exemplo, o ponto é uma figura geométrica sem
dimensão, ou seja 0-dimensional, a reta é 1-dimensional, o triângulo
é 2-dimensional e o cubo é 3-dimensional. Às vezes, simplesmente
escrevemos que o cubo é 3D.
figura plana É uma figura em duas dimensões, como o círculo, o
quadrado, o pentágono, o trapézio, etc.
fração Representa as partes de um todo ou de um conjunto, a razão
entre dois números inteiros ou uma divisão.
fração decimal Um numero fracionário que expressa uma forma
decimal como 4,8 ou 7,23.
4,8=24/5
7,23 = 723/100
fração irredutível Uma fração onde o numerador e o denominador
não têm um fator comum maior do que 1. A fração 3/4 é irredutível,
mas 5/25 não é.
fração ordinária É a fração que não é decimal. A fração 1/4 é
ordinária.

14. fração simplificada ver fração irredutível
frações equivalentes São frações que representam a mesma
quantidade. As frações 1/2, 2/4 e 8/16 são equivalentes.
fundo de um gráfico Geralmente é a região sobre a qual um
desenho é colocado.
gabarito Um modelo que permite reproduzir figuras.
geoplano Uma prancheta de madeira ou de plástico composta de
pregos ou metais disposta em quadrado, permitindo a construção de
vários polígonos e aprofundamento de uma variedade de conceitos
geométricos.
gráfico Um quadro que permite representar os dados.
gráfico de barras Um gráfico onde os dados são representados com
faixas verticais ou horizontais.
gráfico de linha Um gráfico formado por uma linha construída pela
ligação de segmentos de reta, unindo os pontos que representam os
dados.

15. grau Unidade de medida de ângulo muito utilizada nos primeiros
níveis educacionais. Ela é obtida pela divisão da circunferência em
360 partes iguais, obtendo-se assim um ângulo de um grau, sendo
que a notação desta medida usa um pequeno º colocado como
expoente do número, como 1º.
heptágono Um polígono com 7 lados.
hexaedro Um prisma retangular que tem as seis faces quadradas.
Cada conjunto de três arestas se encontra num ponto denominado
vértice e duas destas arestas sempre formam um ângulo reto. As
seis faces são paralelas duas a duas.
hexágono Um polígono com 6 lados.

16. histograma Um diagrama com faixas representando valores
contínuos.
icosaedro Um poliedro com 20 faces.
inclinação de uma reta Se dois pontos de uma reta têm a mesma
abscissa, diz-se que a reta é vertical e se as abscissas são
diferentes a reta é inclinada. Quando é possível, a inclinação é
obtida pela divisão entre a diferença das ordenadas e a diferença
das abscissas de dois pontos quaisquer.
infinito Que não é finito. O conjunto dos números naturais é infinito,
pois sempre existirá um outro natural que supera o anterior.
Significa algo tão grande que não pode ser contado.
interseção A interseção de dois conjuntos é o conjunto de todos os
elementos que pertencem aos dois conjuntos simultaneamente. A
interseção dos conjuntos A e B é denotada por A B e lê-se "A
interseção B". A interseção de conjuntos satisfaz as seguintes
propriedades:
1. A A = A e A Ø=Ø
2. A B = B A (A interseção é comutativa)
3. (A B) C = A (B C) (A interseção é associativa).
intervalo Um intervalo finito da reta real R é um subconjunto de R
que possui uma das seguintes formas:
1. [a,b]={x real: a<×< b}

17. 2. (a,b)={x real: a<×< b}
3. [a,b)={x real: a<×< b}
4. (a,b]={x real: a<×< b}
linha Uma figura geométrica 1D ou seja unidimensional.
linha de tempo Colocação de eventos em ordem cronológica
juntamente com os períodos ou datas das ocorrências dos fatos.
losango Um paralelogramo com quatro lados iguais, dois a dois
paralelos, sendo que os ângulos opostos obtidos a partir de uma
mesma diagonal são iguais.
massa A massa de um objeto é a propriedade de ser mais ou
menos pesada. A massa de um objeto depende de seu volume e da
matéria de que o objeto é constituído. O peso de um objeto, além
disso, depende do local onde se encontra (sobre a Terra ou sobre a
Lua, no Polo Sul ou sobre a Linha do Equador...): o peso mede a
força com a qual o objeto é arremessado.
mil 10³=1000. 1 seguido de três zeros.
milhão 106=1000000. Número 1 seguido de seis zeros.
milhar 10³=1000. 1 seguido de três zeros.
milheiro 10³=1000. 1 seguido de três zeros.
modelo Ver motivo e motivo numérico.
módulo Ver valor absoluto
multiplicação Uma das quatro operações básicas da aritmética, que
realiza o produto de dois ou mais termos denominados fatores. A

18. multiplicação é uma adição repetida: 8x4 é a mesma coisa que
8+8+8+8=32.
multiplicador O número pelo qual se multiplica. No produto 8x4=32,
4 é o multiplicador.
multiplicando O número que será multiplicado por outro. No produto
8x4=32, 8 é o multiplicando.
múltiplo Um múltiplo de um número inteiro é o produto deste número
por um outro número inteiro. 0, 4, 8, 16... são múltiplos de 4.
multívoca Correspondência de um objeto com vários. Por exemplo,
um carro de $10.000,00 corresponde a dez motos de $1.000,00,
pelo menos em termos monetários.
numerador Indica o número de partes em consideração com o todo.
Na fração é o número que fica em cima. É o número que é dividido
pelo número de baixo. Na fração 3/4 o numerador é o número 3.
número Um símbolo que representa uma quantidade, uma
grandeza, uma posição. Os símbolos utilizados podem ser de
algarismos (26), de letras (vinte e seis) ou outros (lA), sendo que
este último é uma mistura de letras e números e corresponde ao
número 26 na base hexadecimal.
número cardinal É o número de elementos de um conjunto. a
característica associada ao número cardinal é a cardinalidade.
número composto É um número que tem mais do que dois divisores
naturais distintos, tais como 4, 6, 12, 15, 49.
número decimal Número no qual a parte inteira é separada da parte
decimal por uma vírgula.
número ímpar Um número inteiro que não é múltiplo de 2. Exemplos
de tais números são:
..., -7, -5, -3, -1, 1, 3, 5, 7, 9, ...

19. número inteiro Números inteiros são os números naturais e seus
opostos, reunidos ao zero.
..., -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, ...
número irracional Um número que não pode ser escrito sob a forma
da divisão de dois números inteiros, tais como pi=3,1415926535... e
e=2,71828...
número misto É um número obtido pela soma de um número inteiro
com uma fração ordinária, como:
2 2
6 =6+
7 7
número natural Números naturais são aqueles provenientes dos
processo de contagem na natureza. Existe discussão sobre o fato
do 0 (zero) ser considerado um número natural uma vez que este foi
criado pelos hindús para dar sentido à nulidade de algo.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ...
número ordinal O ordinal de um número exprime sua posição em
uma sequência, tal como primeiro, segundo, terceiro, vigésimo.
número par Um número inteiro que é múltiplo de dois. Exemplos de
tais números são:
..., -6, -4, -2, 0, 2, 4, 6, 8, ...
número primo Um número inteiro maior do que 1, que não é divisível
por qualquer outro número exceto por ele e por 1. Um número primo
tem somente dois divisores naturais diferentes.
número racional Um número que pode ser colocado sobre a forma
de uma fração, sendo que o numerador e o denominador devem ser
dois números inteiros, sendo que o denominador não pode ser zero
(0).

20. octaedro Um poliedro com 8 faces.
octógono Um polígono com 8 lados.
ordem Arranjo ordenado que pode ser em ordem crescente ou
decrescente. Existe um padrão de comportamento para os objetos.
ordem crescente Arranjo de um grupo de números em ordem, de
modo que um número menor é sempre colocado antes de um maior.
Exemplo: 3, 6, 9, 12, 27.
ordem decrescente Arranjo de um grupo de números em ordem, de
modo que um número maior é colocado antes de um menor.
Exemplo: 27, 12, 9, 6, 3.
ordenada Ver coordenadas.
padrão Um procedimento onde se utilisa as figuras congruentes
repetidas, seja para recobrir uma superfície ou para criar uma
borda. É também uma regularidade, um modelo, uma sequência:
quando se pode identificar o próximo evento ou objeto que virá, se
encontrou um padrão.
padrão numérico Uma regularidade, um modelo, uma sequência:
quando se pode identificar o próximo número que virá, se se
encontrou um padrão numérico.
par Um número inteiro que é divisível por 2. Também entendido
como um conjunto que contem dois elementos.

21. paralelepipedo Sólido geométrico com seis faces, sendo que as
faces opostas são paralelas. Este sólido se assemelha a uma caixa
de sapato.
paralelogramo Um quadrilátero que tem os lados opostos paralelos.
pentadecágono Um polígono com 15 lados.
pentágono Um polígono com 5 lados.
pentominó Todas as figuras em duas dimensões formadas pela
combinação de 5 quadrados congruentes adjacentes.
perímetro O comprimento da curva em torno de uma figura fechada
e limitada.

22. perímetro da circunferência É a medida do comprimento da
circunferência. Se esta tem o raio igual a r e Pi é a constante cujo
valor é 3,1415926535..., então o perímetro P é calculado por:
P = 2 × Pi × r
peso Ver massa.
pictograma Um gráfico no qual os dados são representados por
desenhos ou imagens.
pirâmide Um poliedro que tem como base um polígono e como
lados, triângulos que se reunem em um ponto comum.
plurívoca Correspondência de vários objetos com vários objetos.
Quatro doces de $5,00 correspondem a cinco doces de $4,00, pelo
menos no preço.
poliedro Um sólido limitado por polígonos.
polígono Uma região plana fechada limitada por segmentos de
retas.

23. polígono circunscrito Um polígono é circunscrito a uma
circunferência se todos os seus lados são tangentes à
circunferência. Neste caso pode-se dizer que a circunferência é
inscrita no polígono.
polígono inscrito Um polígono é inscrito a uma circunferência se
todos os seus vértices são pontos da circunferência. Neste caso
podemos dizer que a circunferência é circunscrita ao polígono.
polígono regular Um polígono que tem todos os ângulos e lados
congruentes.
ponto Uma figura geométrica sem dimensão.
ponto de referência Um dado conhecido que nos permite estimar
uma quantidade desconhecida.
predição A declaração de que se deve chegar, fundamentada no
raciocínio ou experiência científica. Pode-se fazer previsões sobre a
meteorologia, tremores de terra, resultados de competições
esportivas, etc.
previsão Ver predição
prisma Um poliedro limitado por dois polígonos paralelos e
congruentes reunidos por dois paralelogramos.
prisma retangular Um prisma que tem polígonos quadriláteros
paralelos e congruentes.

24. prisma triangular Um prisma que tem polígonos triangulares
paralelos e congruentes.
probabilidade É o quociente entre o número de casos favoráveis e o
número total de casos possíveis em uma experiência. A
probabilidade de obter o número 4 no lançamento de um dado sem
defeito é 1/6.
produto Uma das quatro operações básicas da aritmética, que
realiza o produto de dois ou mais termos denominados fatores. A
multiplicação é uma adição repetida: 8x4 é a mesma coisa que
8+8+8+8=32.
quadrado Um quadrilátero que tem todos os quatro ângulos retos e
os quatro lados congruentes, paralelos dois a dois.
quadrado mágico Os números são dispostos em quadrados (3x3,
4x4, 5x5, ...) de modo que a soma dos números na vertical, na
horizontal ou na diagonal é sempre a mesma. Apresentamos dois
quadrados mágicos, o primeiro com os números 1, 2 e 3 e o outro
com os números 1, 2, 3, 4, 5, 6, 7, 8 e 9. As tabelas foram postas ao
lado para aproveitar o espaço.
1 3 2 8 1 6
3 2 1 3 5 7
2 1 3 4 9 2
quadrante Uma região do plano cartesiano delimitada por duas
semi-retas. O plano cartesiano possui 4 quadrantes.

25. quadrilátero Um polígono com quatro lados.
quociente O resultado de uma divisão. Na divisão de 8 por 4 o
quociente é 2
radiano É a unidade de medida de ângulo no Sistema Internacional,
o procedimento para obter um radiano é o seguinte: Tomamos um
segmento de reta OA. Com um compasso centrado no ponto O e
abertura OA, traçamos um arco de circunferência AB, sendo que B
deve pertencer ao outro lado do ângulo AOB. Se o comprimento do
arco for igual ao comprimento do segmento OA, diremos que este
ângulo tem medida igual a 1 radiano (1 rad).
raio O segmento de reta que liga o centro do círculo a qualquer
ponto da circunferência do círculo.
rede Obtém um padrão quando se desenvolve um sólido, isto é, se
estende a superfície exterior de um sólido para obter uma superfície
plana.
reflexão A formação dos pontos de um objeto de modo que a nova
figura obtida se pareça como uma imagem refletida em um espelho.

26. relação de Euler (lê-se:"Óiler") Num poliedro convexo, a soma do
número V de vértices com o número F de faces é igual ao número A
de arestas mais dois.
V+F = A+2
resto A quantidade que sobra após a divisão de um número inteiro
por outro. Ao dividir 13 por 4, o quociente é 3 e o resto é 1.
reta (Conceito primitivo) É um conjunto infinito de pontos alinhados
de tal forma que os segmentos com extremidades em dois
quaisquer desses pontos têm sempre a mesma inclinação.
reta numerada Uma reta graduada que tem o número 0 (zero) como
ponto inicial, um número 1 (unidade) como ponto de referência e
outros números em ordem crescente (por convençao: para a
direita), relativamente à medida do segmento que começa em 0 e
termina em 1.
retângulo Um paralelogramo que tem 4 ângulos retos e os lados são
paralelos e congruentes dois a dois.
retas concorrentes Retas que se cruzam.

27. retas oblíquas Duas retas que se cortam com um ângulo não
perpendicular.
retas paralelas Retas que nunca se cruzam e que não estão
sobrepostas.
retas perpendiculares Retas que se cruzam formando um ângulo
reto.
revolução Um deslocamento no qual cada ponto do objeto se
desloca mantendo a mesma distância ao centro de rotação mas
formando ângulos diferentes. Por exemplo, o movimento da roda de
uma bicicleta é um movimento de rotação em torno de um eixo.
rombo Ver losango.
rotação Um deslocamento no qual cada ponto do objeto se desloca
mantendo a mesma distância ao centro de rotação mas formando
ângulos diferentes. Por exemplo, o movimento da roda de uma
bicicleta é um movimento de rotação em torno de um eixo.
segmento de reta Uma parte de uma reta limitada entre dois pontos.
semelhante Diz-se que duas figuras são semelhantes se ambas são
congruentes ou uma delas é uma ampliação ou redução da outra.

28. sentença numérica Ver expressão numérica
simetria com respeito a um ponto Quando uma figura é rodada de
um ângulo de 1140 graus, pode-se dizer que ela é simétrica com
respeito a um ponto.
simetria de rotação Ver simetria com respeito a um ponto
simetria com respeito a uma reta Quando uma figura é rebatida em
relação a uma reta, diz-se que ela é a reflexão de uma outra figura
ou simétrica em relação a uma reta.

29. simétrico Uma figura em uma, duas ou três dimensões é dita
simétrica se ela possui um ente de simetria (ponto, eixo ou plano),
de modo que do outro lado deste ente de simetria a figura seja
semelhante porem invertida como se tivesse sido colocada na frente
de um espelho.
sólido Uma figura em três dimensões. Exemplos de sólidos são:
cubo, paralelepípedo, pirâmide.
soma Uma das principais operações básicas da aritmética, que
resulta na adição de números.
2+3=(1+1)+(1+1+1)=(1+1+1+1+1)=5
subtração Uma das quatro operações básicas da aritmética, que
objetiva retirar um número de outro. É uma operação artificial criada
a partir da adição.
5-3=(1+1+1+1+1)-(1+1+1)=(1+1)=2
superfície Um ente geométrico bidimensional suave (que não possui
bicos ou autointerseções) que possui medida de área, isto é, uma
região que pode ser planificada (colocada sobre um plano) de modo
que a nova região planificada tenha a área equivalente à de um
quadrado.

30. tangram Conjunto de peças gráficas específicas que pode ser
reunido para montar figuras geométricas. Muito utilizado nas
atividades práticas de Geometria.
tentativa e erro, chute Uma estratégia de resolução de problemas
onde se faz uma escolha para viabilizar o resultado e assim se
procede várias vezes até que que se chegue a alguma conclusão
próxima ao objetivo para a resolução do problema.
termo Um dos objetos matemáticos em uma operação.
tetraedro Um poliedro com 4 faces. Se o tetraedro for regular, ele
terá 4 faces congruentes, 4 vértices e 6 arestas também
congruentes.
total O resultado de uma adição ou de um produto.
transferidor Um instrumento que serve para medir ângulos.
translação O deslocamento paralelo em linha reta de um objeto ou
figura. Um elevador realiza uma operação de translação.
trapezóide Um quadrilátero que tem dois lados paralelos.
triângulo Um polígono com três lados.
valor absoluto O valor absoluto de um número real a também
chamado "módulo de a" é denotado por |a| e definido como o
máximo valor entre a e -a, isto é:
|a|=max{a,-a}
valor posicional O valor da posição de um algarismo depende de
sua posição no número. No número 728, o algarismo 7 ocupa a

31. posição das centenas, o 2 ocupa a posição das dezenas e o 8 a
posição das unidades.
vértice O ponto de junção de duas semi-retas de um ângulo, de dois
lados de um polígono ou de três (ou mais) faces de um sólido.
vetor nulo Vetor nulo ou vetor zero de um esapaço vetorial,
denotado neste trabalho por Ö.
vírgula É um sinal matemático que separa a parte inteira da parte
decimal de um número.
Pi = 3,1415926535
volume O volume de um objeto é definido como a medida do lugar
ocupado pelo objeto no espaço. Por exemplo, o volume de uma
caixa é medido em cm³. No contexto das artes visuais, o volume
representa uma característica do objeto e não uma medida do
espaço ocupado.
2- Ensino Fundamental: A origem dos números
A origem dos números Sistema Indo-Arábico
Início do processo de contagem Histórico: notação Posicional
Representação numérica Histórico: criação do zero
Alguns símbolos antigos Notação Posicional
O ábaco Sistema numérico Romano
Introdução sobre a origem dos números
Você já usou muitas vezes os números, mas será que já parou para
pensar sobre:
a. O modo como surgiram os números?
b. Como foram as primeiras formas de contagem?
c. Como os números foram criados, ou, será que eles sempre
existiram?

32. Para descobrir sobre a origem dos números, precisamos estudar um
pouco da história humana e entender os motivos religiosos desses
criadores. Na verdade, desconhecemos qualquer outro motivo que
tenha gerado os números.
Os historiadores são auxiliados por diversas descobertas, como o
estudo das ruínas de antigas civilizações, estudos de fósseis, o
estudo da linguagem escrita e a avaliação do comportamento de
diversos grupos étnicos desde o princípio dos tempos.
Olhando ao redor, observamos a grande presença dos números.
Quanto mais voltarmos na história, veremos que menor é a
presença dos números.
O Início do processo de contagem
Os homens primitivos não tinham necessidade de contar, pois o que
necessitavam para a sua sobrevivência era retirado da própria
natureza. A necessidade de contar começou com o
desenvolvimento das atividades humanas, quando o homem foi
deixando de ser pescador e coletor de alimentos para fixar-se no
solo.

33. O homem começou a plantar, produzir alimentos, construir casas,
proteções, fortificações e domesticar animais, usando os mesmos
para obter a lã e o leite, tornando-se criador de animais domésticos,
o que trouxe profundas modificações na vida humana.
As primeiras formas de agricultura de que se tem notícia, foram
criadas há cerca de dez mil anos na região que hoje é denominada
Oriente Médio.
A agricultura passou então a exigir o conhecimento do tempo, das
estações do ano e das fases da Lua e assim começaram a surgir as
primeiras formas de calendário.
No pastoreio, o pastor usava várias formas para controlar o seu
rebanho. Pela manhã, ele soltava os seus carneiros e analisava ao
final da tarde, se algum tinha sido roubado, fugido, se perdido do
rebanho ou se havia sido acrescentado um novo carneiro ao
rebanho. Assim eles tinham a correspondência um a um, onde cada
carneiro correspondia a uma pedrinha que era armazenada em um
saco.
No caso das pedrinhas, cada animal que saía para o pasto de
manhã correspondia a uma pedra que era guardada em um saco de
couro. No final do dia, quando os animais voltavam do pasto, era
feita a correspondência inversa, onde, para cada animal que

34. retornava, era retirada uma pedra do saco. Se no final do dia
sobrasse alguma pedra, é porque faltava algum dos animais e se
algum fosse acrescentado ao rebanho, era só acrescentar mais uma
pedra. A palavra que usamos hoje, cálculo, é derivada da palavra
latina calculus, que significa pedrinha.
A correspondência unidade a unidade não era feita somente com
pedras, mas eram usados também nós em cordas, marcas nas
paredes, talhes em ossos, desenhos nas cavernas e outros tipos de
marcação.
Os talhes nas barras de madeira, que eram usados para marcar
quantidades, continuaram a ser usados até o século XVIII na
Inglaterra. A palavra talhe significa corte. Hoje em dia, usamos
ainda a correspondência unidade a unidade.
Representação numérica
Com o passar do tempo, as quantidades foram representadas por
expressões, gestos, palavras e símbolos, sendo que cada povo
tinha a sua maneira de representação.
A faculdade humana natural de reconhecimento imediato de
quantidades se resume a, no máximo, quatro elementos. Este senso
numérico que é a faculdade que permite reconhecer que alguma

35. coisa mudou em uma pequena coleção quando, sem seu
conhecimento direto, um objeto foi tirado ou adicionado, à coleção.
O senso numérico não pode ser confundido com contagem, que é
um atributo exclusivamente humano que necessita de um processo
mental.
"Distingüimos, sem erro e numa rápida vista um, dois, três e mesmo
quatro elementos. mas aí para nosso poder de identificação dos
números." História Universal dos Algarismos", Georges Ifrah.
Temos também, alguns animais, ditos irracionais, como os rouxinóis
e os corvos, que possuem este senso numérico onde reconhecem
quantidades concretas que vão de um até três ou quatro unidades.
Existe um exemplo célebre sobre um corvo que tinha capacidade de
reconhecer quantidades.
Curiosidade: Um fazendeiro estava disposto a matar
um corvo que fez seu ninho na torre de observação
de sua mansão. Por diversas vezes, tentou
surpreender o pássaro, mas em vão: à aproximação
do homem, o corvo saía do ninho. De uma árvore distante, ele
esperava atentamente até que o homem saísse da torre e só então
voltava ao ninho. Um dia, o fazendeiro tentou um ardil: dois homens
entraram na torre, um ficou dentro e o outro saiu e se afastou. Mas
o pássaro não foi enganado: manteve-se afastado até que o outro

36. homem saísse da torre. A experiência foi repetida nos dias
subsequentes com dois, três e quatro homens, ainda sem sucesso.
Finalmente, foram utilizados cinco homens como antes, todos
entraram na torre e um permaneceu lá dentro enquanto os outros
quatro saíam e se afastavam. Desta vez o corvo perdeu a conta.
Incapaz de distinguir entre quatro e cinco, voltou imediatamente ao
ninho.
Alguns símbolos antigos
No começo da história da escrita de algumas civilizações como a
egípcia, a babilônica e outras, os primeiros nove números inteiros
eram anotados pela repetição de traços verticais:
I II III IIII IIIII IIIIII IIIIIII IIIIIIII IIIIIIIII
1 2 3 4 5 6 7 8 9
Depois este método foi mudado, devido à dificuldade de se contar
mais do que quatro termos:
IIII
IIII IIII IIII IIII
I II III IIII IIII
I II III IIII
I
1 2 3 4 5 6 7 8 9
Um dos sistemas de numeração mais antigos que se tem notícia é o
egípcio. É um sistema de numeração de base dez e era composto
pelos seguintes símbolos numéricos:

37. Outro sistema de numeração muito importante foi o da Babilônia,
criado a aproximadamente 4 mil anos.
Algumas das primeiras formas de contagem foram utilizadas com as
partes do corpo humano, sendo que em algumas aldeias os
indivíduos chegavam a contar até o número 33.
O ábaco
O ábaco, em sua forma geral, é uma moldura retangular com fileiras
de arame, cada fileira representando uma classe decimal diferente,
nas quais correm pequenas bolas
No princípio, os sistemas de numeração não facilitavam os cálculos,
logo, um dos instrumentos utilizados para facilitar os cálculos foi o
ábaco muito usado por diversas civilizações orientais e ocidentais.

38. No Japão, o ábaco é chamado de soroban e na China de suánpan,
que significa bandeja de calcular.
O Sistema de numeração Indo-Arábico
Nosso sistema de numeração surgiu na Ásia, há muitos séculos no
Vale do rio Indo, onde hoje é o Paquistão.
O primeiro número inventado foi o 1 e ele significava o homem e
sua unicidade, o segundo número 2, significava a mulher da família,
a dualidade e o número 3 (três) significava muitos, multidão. A
curiosidade sobre os nomes do 3, não deve ter ocorrido por acaso.
Inglês Francês Latim Grego Italiano Espanhol
three trois tres treis tre tres
Sueco Alemão Russo Polonês Hindu Português
tre drei tri trzy tri três
Notas históricas sobre a atual notação posicional
Foi no Norte da Índia, por volta do século V da era cristã, que
nasceu o mais antigo sistema de notação próximo do atual, o que é
comprovado por vários documentos, além de ser citado por árabes
(a quem esta descoberta foi atribuída por muitos anos).
Antes de produzir tal sistema, os habitantes da Índia setentrional
usaram por muito tempo uma numeração rudimentar que aparece
em muitas inscrições do século III antes de Cristo.
Esta numeração tinha uma característica do sistema moderno. Seus
nove primeiros algarismos eram sinais independentes:
1, 2, 3, 4, 5, 6, 7, 8, 9
o que significava que um número como o 5 não era entendido como
5 unidades mas como um símbolo independente.

39. Por muito tempo, estes algarismos foram denominados algarismos
arábicos, de uma forma errada.
Ainda existia nesta época a dificuldade posicional e os hindus
passaram a usar a notação por extenso para os números, pois não
podiam exprimir grandes números por algarismos.
Sem saber, estavam criando a notação posicional e também o zero.
Cada algarismo tinha um nome:
1 2 3 4 5 6 7 8 9
eka dvi tri catur pañca sat sapta asta nava
Quando foi criada pelos hindús a base 10, cada dezena, cada
centena e cada milhar, recebeu um nome individual:
10 = dasa
100 = sata
1.000 = sahasra
10.000 = ayuta
100.000 = laksa
1.000.000 = prayuta
10.000.000 = koti
100.000.000 = vyarbuda
1.000.000.000 = padma
Ao invés de fazer como hoje, de acordo com as potências
decrescentes de 10, os hindus escreviam os números em ordem
crescente das potências de 10 por volta do século IV depois do
nascimento de Jesus Cristo. Eles começavam pelas unidades,

40. depois pelas dezenas, pelas centenas e assim por diante. O número
3.709 ficava:
9 700 3000
nove sete centos três mil
nava sapta sata tri sahasra
Poderiamos escrever o número 12.345 como
pañca caturdasa trisata dvisahasra ayuta
pois, 12.345 = 5 + 40 + 300 + 2.000 + 10.000, logo:
5 = pañca
40 = catur dasa
300 = tri sata
2.000 = dvi sahasra
10.000 = ayuta
pañca caturdasa trisata dvisahasra ayuta
Esta já era uma forma especial.
Em virtude da grande repetição que ocorria com as potências de 10,
por volta do século V depois do nascimento de Jesus Cristo, os
matemáticos e astrônomos hindus resolveram abreviar a notação
retirando os múltiplos de 10 que apareciam nos números grandes,
assim o número 12.345 que era escrito como:
pañca caturdasa trisata dvisahasra ayuta
passou a ser escrito apenas:
54321 = pañca catur tri dvi dasa

41. 12345 = 5 + 4×10 + 3×100 + 2×1000 + 1×10000
e esta se transformou em uma notação falada e escrita posicional
excelente para a época, mas começaram a acontecer alguns
problemas como escrever os números 321 e 301.
321 = 1 + 2 x 10 + 3 x 100
321 = dasa dvi tri
301 = 1 + 3 x 100
301 = dasa tri
É lógico que este último número não poderia ser o 31, pois:
31 = 1 + 3 x 10
31 = dasa tri
No número 301 faltava algo para representar as dezenas.
Para construir este material, usamos algumas partes do excelente
livro: "Os números: A história de uma grande invenção", Georges
Ifrah, Editora Globo, 3a.edição, 1985, com a permissão da Editora.
Notas históricas sobre a criação do zero
Tendo em vista o problema na construção dos números como 31 e
301, os hindus criaram um símbolo para representar algo vazio
(ausência de tudo) que foi denominado sunya (a letra s tem um
acento agudo e a letra u tem um traço horizontal sobre ela).
Dessa forma foi resolvido o problema da ausência de um algarismo
para representar as dezenas no número 301 e assim passaram a
escrever:
301 = 1 + ? x 10 + 3 x 100
301 = dasa sunya tri

42. Os hindus tinham acabado de descobrir o zero.
Porém, estas notações só serviam para as palavras e não para os
números, mas reunindo essas idéias apareceram juntos o zero bem
como o atual sistema de notação posicional.
Um dos primeiros locais onde aparece a notação posicional é um
tratado de cosmologia denominado: Lokavibhaga, publicado na data
de 25 de agosto de 458 do calendário juliano, por um movimento
religioso hindú para enaltecer as suas próprias qualidades
científicas e religiosas. Neste texto, aparece o número 14.236.713
escrito claramente:
triny ekam sapta sat trini dve catvary ekakam
três um sete seis três dois quatro um
Escrever tais números na ordem invertida, fornece:
um quatro dois três seis sete um três
1 4 2 3 6 7 1 3
Números como 123.000 eram escritos como:
sunya sunya sunya tri dvi dasa
que significa:
zero zero zero três dois um
que escrito na ordem invertida fornece:
um dois três zero zero zero
No texto existe a palavra hindú sthanakramad que significa "por
ordem de posição".

43. Observamos que tal notação posicional já era então conhecida no
quinto século de nossa era por uma grande quantidade de cientistas
e matemáticos.
Para escrever este material, usamos alguns tópicos do excelente
livro: "Os números: A história de uma grande invenção", Georges
Ifrah, Editora Globo, 3a.edição, 1985.
Notação Posicional
O sistema de numeração posicional indiano surgiu por volta do
século V. Este princípio de numeração posicional já aparecia nos
sistemas dos egípcios e chineses.
No sistema de numeração indiana não posicional que aparece no
século I não existia a necessidade do número zero.
Notação (ou valor) posicional é quando representamos um número
no sistema de numeração decimal, sendo que cada algarismo tem
um determinado valor, de acordo com a posição relativa que ele
ocupa na representação do numeral.
Mudando a posição de um algarismo, estaremos alterando o valor
do número. Por exemplo, tomemos o número 12. Mudando as
posições dos algarismos teremos 21.
12 = 1 × 10 + 2
21 = 2 × 10 + 1
O zero foi o último número a ser inventado e o seu uso matemático
parece ter sido criado pelos babilônios. Os documentos mais
antigos conhecidos onde aparece o número zero, não são
anteriores ao século III antes de Cristo. Nesta época, os números
continham no máximo três algarismos.
Um dos grandes problemas do homem começou a ser a
representação de grandes quantidades. A solução para isto foi
instituir uma base para os sistemas de numeração. Os numerais
indo-arábicos e a maioria dos outros sistemas de numeração usam

44. a base dez, isto porque o princípio da contagem se deu em
correspondência com os dedos das mãos de um indivíduo normal.
Na base dez, cada dez unidades é representada por uma dezena,
que é formada pelo número um e o número zero: 10.
A base dez já aparecia no sistema de numeração chinês.
Os sumérios e os babilônios usavam a base sessenta.
Alguma vez você questionou sobre a razão pela qual há 360 graus
em um círculo? Uma resposta razoável é que 360=6x60 e 60 é um
dos menores números com grande quantidade de divisores, como
por exemplo:
D(60) = { 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60}
Os indianos reuniram as diferentes características do princípio
posicional e da base dez em um único sistema numérico. Este
sistema decimal posicional foi assimilado e difundido pelos árabes e
por isso, passou a ser conhecido como sistema indo-arábico.
Nosso sistema de numeração retrata o ábaco. Em cada posição que
um número se encontra seu valor é diferente.
O Sistema Romano de Numeração
O sistema de numeração Romano é um sistema decimal, ou seja,
sua base é dez. Este sistema é utilizado até hoje em
representações de séculos, capítulos de livros, mostradores de
relógios antigos, nomes de reis e papas e outros tipos de
representações oficiais em documentos. Estas eram as primeiras
formas da grafia dos algarismos romanos.
Tal sistema não permite que sejam feitos cálculos, não se
destinavam a fazer operações aritméticas mas apenas representar
quantidades. Com o passar do tempo, os símbolos utilizados pelos
romanos eram sete letras, cada uma com um valor numérico:

45. Letra I V X L C D M
Valor 1 5 10 50 100 500 1000
Leitura Um Cinco Dez Cinquenta Cem Quinhentos Mil
Estas letras obedeciam aos três princípios:
1. Todo símbolo numérico que possui valor menor do que o
que está à sua esquerda, deve ser somado ao maior.
VI = 5 + 1 = 6
XII = 10 + 1 + 1 = 12
CLIII = 100 + 50 + 3 = 153
2. Todo símbolo numérico que possui valor menor ao que está
à sua direita, deve ser subtraído do maior.
IX = 10 - 1 = 9
XL = 50 - 10 = 40
VD = 500 - 5 = 495
3. Todo símbolo numérico com um traço horizontal sobre ele
representa milhar e o símbolo numérico que apresenta dois
traços sobre ele representa milhão.
3- Ensino Fundamental: Números Naturais: Primeira
parte
Introdução aos Nos. Naturais Propriedades da
A construção dos Nos. Naturais multiplicação
Igualdade e Desigualdades Propriedade Distributiva
Operações com Nos. Naturais Divisão de Números Naturais
Adição de Números naturais Potenciação de Nos. Naturais
Propriedades da Adição Propriedades da Potenciação
Curiosidade: Tabela de adição Números grandes

46. Multiplicação de Nos. Naturais Exercícios
Introdução aos Números Naturais
O conjunto dos números naturais é representado pela letra
maiúscula N e estes números são construídos com os
algarismos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, que também são
conhecidos como algarismos indo-arábicos. No século VII, os
árabes invadiram a Índia, difundindo o seu sistema numérico.
Embora o zero não seja um número natural no sentido que tenha
sido proveniente de objetos de contagens naturais, iremos
considerá-lo como um número natural uma vez que ele tem as
mesmas propriedades algébricas que os números naturais. Na
verdade, o zero foi criado pelos hindus na montagem do sistema
posicional de numeração para suprir a deficiência de algo nulo. Para
saber mais, clique nos links: Notas históricas sobre o zero ou
Notação Posicional. Caso queira se aprofundar no assunto, veja o
belíssimo livro: "História Universal dos Algarismos, Tomos I e II,
Editora Nova Fronteira, 1998 e 1999", de Georges Ifrah.
Na sequência consideraremos que os naturais têm início com o
número zero e escreveremos este conjunto como:
N = { 0, 1, 2, 3, 4, 5, 6, ...}
Representaremos o conjunto dos números naturais com a letra N.
As reticências (três pontos) indicam que este conjunto não tem fim.
N é um conjunto com infinitos números.
Excluindo o zero do conjunto dos números naturais, o conjunto será
representado por:
N* = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
A construção dos Números Naturais
1. Todo número natural dado tem um sucessor (número que
vem depois do número dado), considerando também o zero.

47. Exemplos: Seja m um número natural.
(a) O sucessor de m é m+1.
(b) O sucessor de 0 é 1.
(c) O sucessor de 1 é 2.
(d) O sucessor de 19 é 20.
2. Se um número natural é sucessor de outro, então os dois
números juntos são chamados números consecutivos.
Exemplos:
(a) 1 e 2 são números consecutivos.
(b) 5 e 6 são números consecutivos.
(c) 50 e 51 são números consecutivos.
3. Vários números formam uma coleção de números naturais
consecutivos se o segundo é sucessor do primeiro, o
terceiro é sucessor do segundo, o quarto é sucessor do
terceiro e assim sucessivamente.
Exemplos:
(a) 1, 2, 3, 4, 5, 6 e 7 são consecutivos.
(b) 5, 6 e 7 são consecutivos.
(c) 50, 51, 52 e 53 são consecutivos.
4. Todo número natural dado n, exceto o zero, tem um
antecessor (número que vem antes do número dado).

48. Exemplos: Se m é um número natural finito diferente de
zero.
(a) O antecessor do número m é m-1.
(b) O antecessor de 2 é 1.
(c) O antecessor de 56 é 55.
(d) O antecessor de 10 é 9.
O conjunto abaixo é conhecido como o conjunto dos números
naturais pares. Embora uma seqüência real seja um outro objeto
matemático denominado função, algumas vezes utilizaremos a
denominação sequência dos números naturais pares para
representar o conjunto dos números naturais pares:
P = { 0, 2, 4, 6, 8, 10, 12, ...}
O conjunto abaixo é conhecido como o conjunto dos números
naturais ímpares, às vezes também chamado, a sequência dos
números ímpares.
I = { 1, 3, 5, 7, 9, 11, 13, ...}
Igualdade e Desigualdades
Diremos que um conjunto A é igual a um conjunto B se, e somente
se, o conjunto A está contido no conjunto B e o conjunto B está
contido no conjunto A. Quando a condição acima for satisfeita,
escreveremos A=B (lê-se: A é igual a B) e quando não for satisfeita
denotaremos tal fato por:
(lê-se: A é diferente de B). Na definição de igualdade de conjuntos,
vemos que não é importante a ordem dos elementos no conjunto.

49. Exemplo com igualdade: No desenho, em anexo, observamos que
os elementos do conjunto A são os mesmos elementos do conjunto
B. Neste caso, A=B.
Consideraremos agora uma situação em que os elementos dos
conjuntos A e B serão distintos.
Sejam A={a,b,c,d} e B={1,2,3,d}. Nem todos os elementos do
conjunto A estão no conjunto B e nem todos os elementos do
conjunto B estão no conjunto A. Também não podemos afirmar que
um conjunto é maior do que o outro conjunto. Neste caso,
afirmamos que o conjunto A é diferente do conjunto B.
Exercício: Há um espaço em branco entre dois números em cada
linha. Qual é o sinal apropriado que deve ser posto neste espaço: <,
> ou =?
159 170
852 321
587 587
Exercício: Representar analiticamente cada conjunto, isto é, através
de alguma propriedade e depois por extensão, apresentando os
elementos:
a. Conjunto N dos números Naturais
b. Conjunto P dos números Naturais Pares
c. Conjunto I dos números Naturais Ímpares
d. Conjunto E dos números Naturais menores que 16
e. Conjunto L dos números Naturais maiores que 11
f. Conjunto R dos números Naturais maiores ou iguais a 28

50. g. Conjunto C dos números Naturais que estão entre 6 e 10
Operações com Números Naturais
Na sequência, estudaremos as duas principais operações possíveis
no conjunto dos números naturais. Praticamente, toda a Matemática
é construída a partir dessas duas operações: adição e multiplicação.
A adição de números naturais
A primeira operação fundamental da Aritmética, tem por finalidade
reunir em um só número, todas as unidades de dois ou mais
números. Antes de surgir os algarismos indo-arábicos, as adições
podiam ser realizadas por meio de tábuas de calcular, com o auxílio
de pedras ou por meio de ábacos.
Propriedades da Adição
1. Fechamento: A adição no conjunto dos números naturais é
fechada, pois a soma de dois números naturais é ainda um
número natural. O fato que a operação de adição é fechada
em N é conhecido na literatura do assunto como: A adição é
uma lei de composição interna no conjunto N.
2. Associativa: A adição no conjunto dos números naturais é
associativa, pois na adição de três ou mais parcelas de
números naturais quaisquer é possível associar as parcelas
de quaisquer modos, ou seja, com três números naturais,
somando o primeiro com o segundo e ao resultado obtido

51. somarmos um terceiro, obteremos um resultado que é igual
à soma do primeiro com a soma do segundo e o terceiro.
3. Elemento neutro: No conjunto dos números naturais, existe o
elemento neutro que é o zero, pois tomando um número
natural qualquer e somando com o elemento neutro (zero), o
resultado será o próprio número natural.
4. Comutativa: No conjunto dos números naturais, a adição é
comutativa, pois a ordem das parcelas não altera a soma, ou
seja, somando a primeira parcela com a segunda parcela,
teremos o mesmo resultado que se somando a segunda
parcela com a primeira parcela.
Curiosidade: Tabela de adição
Para somar dois números, com a tabela, um em uma linha e outro
em uma coluna, basta fixar um número na 1a. coluna e um segundo
número na 1a. linha. Na interseção da linha e coluna fixadas,
obtemos a soma dos números.
0 1 2 3 4 5 6 7 8 9 10
1 2 3 4 5 6 7 8 9 10 11
2 3 4 5 6 7 8 9 10 11 12
3 4 5 6 7 8 9 10 11 12 13

52. 4 5 6 7 8 9 10 11 12 13 14
5 6 7 8 9 10 11 12 13 14 15
6 7 8 9 10 11 12 13 14 15 16
7 8 9 10 11 12 13 14 15 16 17
8 9 10 11 12 13 14 15 16 17 18
9 10 11 12 13 14 15 16 17 18 19
10 11 12 13 14 15 16 17 18 19 20
11 12 13 14 15 16 17 18 19 20 21
Por exemplo, se tomarmos o número 7 na linha horizontal e o
número 6 na linha vertical, obteremos a soma 13 que está no
cruzamento da linha do 7 com a coluna do 6.
Multiplicação de Números Naturais
É a operação que tem por finalidade adicionar o primeiro número
denominado multiplicando ou parcela, tantas vezes quantas são as
unidades do segundo número denominado multiplicador.
Exemplo: 4 vezes 9 é somar o número 9 quatro vezes:
4 x 9 = 9 + 9 + 9 + 9 = 36
O resultado da multiplicação é denominado produto e os números
dados que geraram o produto, são chamados fatores. Usamos o
sinal × ou · ou x, para representar a multiplicação.
Propriedades da multiplicação
1. Fechamento: A multiplicação é fechada no conjunto N dos
números naturais, pois realizando o produto de dois ou mais
númros naturais, o resultado estará em N. O fato que a
operação de multiplicação é fechada em N é conhecido na

53. literatura do assunto como: A multiplicação é uma lei de
composição interna no conjunto N.
2. Associativa: Na multiplicação, podemos associar 3 ou mais
fatores de modos diferentes, pois se multiplicarmos o
primeiro fator com o segundo e depois multiplicarmos por um
terceiro número natural, teremos o mesmo resultado que
multiplicar o terceiro pelo produto do primeiro pelo segundo.
(m.n).p = m.(n.p)
(3.4).5 = 3.(4.5) = 60
3. Elemento Neutro: No conjunto dos números naturais existe
um elemento neutro para a multiplicação que é o 1.
Qualquer que seja o número natural n, tem-se que:
1.n = n.1 = n
1.7 = 7.1 = 7
4. Comutativa: Quando multiplicamos dois números naturais
quaisquer, a ordem dos fatores não altera o produto, ou seja,
multiplicando o primeiro elemento pelo segundo elemento
teremos o mesmo resultado que multiplicando o segundo
elemento pelo primeiro elemento.
m.n = n.m
3.4 = 4.3 = 12
Propriedade Distributiva
Multiplicando um número natural pela soma de dois números
naturais, é o mesmo que multiplicar o fator, por cada uma das
parcelas e a seguir adicionar os resultados obtidos.

54. m.(p+q) = m.p + m.q
6x(5+3) = 6x5 + 6x3 = 30 + 18 = 48
Divisão de Números Naturais
Dados dois números naturais, às vezes necessitamos saber
quantas vezes o segundo está contido no primeiro. O primeiro
número que é o maior é denominado dividendo e o outro número
que é menor é o divisor. O resultado da divisão é chamado
quociente. Se multiplicarmos o divisor pelo quociente obteremos o
dividendo.
No conjunto dos números naturais, a divisão não é fechada, pois
nem sempre é possível dividir um número natural por outro número
natural e na ocorrência disto a divisão não é exata.
Relações essenciais numa divisão de números naturais
1. Em uma divisão exata de números naturais, o divisor deve
ser menor do que o dividendo.
35 : 7 = 5
2. Em uma divisão exata de números naturais, o dividendo é o
produto do divisor pelo quociente.
35 = 5 x 7
3. A divisão de um número natural n por zero não é possível
pois, se admitíssemos que o quociente fosse q, então
poderiamos escrever:

55. n÷0=q
e isto significaria que:
n=0xq=0
o que não é correto! Assim, a divisão de n por 0 não tem
sentido ou ainda é dita impossível.
Exercício: Substituindo X por 6 e Y por 9, qual é o valor da soma do
dobro de X pelo triplo de Y.
Potenciação de Números Naturais
Para dois números naturais m e n, a expressão mn é um produto de
n fatores iguais ao número m, ou seja:
mn = m . m . m ... m . m
m aparece n vezes
O número que se repete como fator é denominado base que neste
caso é m. O número de vezes que a base se repete é denominado
expoente que neste caso é n. O resultado é donominado potência.
Esta operação não passa de uma multiplicação com fatores iguais,
como por exemplo:
23 = 2 × 2 × 2 = 8
43 = 4 × 4 × 4 = 64
Propriedades da Potenciação
1. Uma potência cuja base é igual a 1 e o expoente natural é n,
denotada por 1n, será sempre igual a 1.
Exemplos:
a. 1n = 1×1×...×1 (n vezes) = 1
b. 13 = 1×1×1 = 1

56. c. 17 = 1×1×1×1×1×1×1 = 1
2. Se n é um número natural não nulo, então temos que no=1.
Por exemplo:
3. (a) nº = 1
4. (b) 5º = 1
5. (c) 49º = 1
6. A potência zero elevado a zero, denotada por 0o, é carente
de sentido no contexto do Ensino Fundamental. O visitante
que necessitar aprofundamento neste assunto, deve visitar
nosso link Zero elevado a zero?
7. Qualquer que seja a potência em que a base é o número
natural n e o expoente é igual a 1, denotada por n1, é igual
ao próprio n. Por exemplo:
8. (a) n¹ = n
9. (b) 5¹ = 5
10. (c) 64¹ = 64
11. Toda potência 10n é o número formado pelo algarismo 1
seguido de n zeros.
Exemplos:
a. 103 = 1000
b. 108 = 100.000.000
c. 10o = 1
Números grandes
No livro "Matemática e Imaginação", o matemático americano
Edward Kasner apresentou um número denominado googol que
pode ser representado por 1 seguido de 100 zeros.
1 Googol = 10100

57. Ele pensou que este era um número superior a qualquer coisa que
passasse pela mente humana sendo maior do que qualquer coisa
que pode ser posta na forma de palavras. Um googol é um pouco
maior do que o número total de partículas elementares conhecidas
no universo, algo da ordem de 1080. Se o espaço com estas
partículas fosse comprimido de uma forma sólida com neutrons,
este ficaria com algo em torno de 10128 partículas.
Outro matemático criou então o googolplex e o definiu como 10
elevado ao googol.
1 Googolplex = 10Googol
Exercícios
1. Na figura abaixo, insira os números 1, 2, 3, 4, 5 e 6 nos
círculos, de tal modo que a soma de cada lado seja sempre
igual a 10.
2. Um gavião viu um grupo de pombos, chegou perto deles e
disse:
3. Olá minhas 100 pombinhas.
4. Uma delas respondeu:
5. Não somos 100 não meu caro gavião,
6. seremos 100, nós, mais dois tantos de nós
7. e mais você meu caro gavião.
8. Quantos pombos há neste grupo?

58. 9. Três homens querem atravessar um rio. O barco que eles
possuem suporta no máximo 150 kg. Um deles pesa 50 kg,
o segundo pesa 75 kg e o terceiro pesa 120 kg. Qual será o
processo para eles atravessarem o rio sem afundar?
10. Forme um quadrado mágico com os números 1, 2, 3, 4,
5, 6, 7, 8 e 9 tal que, a soma dos números de qualquer linha,
qualquer coluna ou qualquer diagonal deverá ser sempre
igual a 15.
4- Ensino Fundamental: Números Naturais: Segunda parte
Múltiplos de Nos. naturais Máximo Divisor Comum
Divisores de Nos. naturais Método para obter o MDC
Números primos Relação entre o MMC e MDC
Crivo de Eratóstenes Primos entre si
Mínimo Múltiplo Comum Radiciação de Nos. naturais
Método para obter o MMC
Múltiplos de números Naturais
Diz-se que um número natural a é múltiplo de outro natural b, se
existe um número natural k tal que:
a=k×b
Exemplos:
(a) 15 é múltiplo de 5, pois 15=3×5.
(b) 24 é múltiplo de 4, pois 24=6×4.
(c) 24 é múltiplo de 6, pois 24=4×6.
(d) 27 é múltiplo de 9, pois 27=3×9.
Se a=k×b, então a é múltiplo de b, mas também, a é múltiplo de k,
como é o caso do número 35 que é múltiplo de 5 e de 7, pois:
35=7×5

59. Se a=k×b, então a é múltiplo de b e se conhecemos b e queremos
obter todos os seus múltiplos, basta fazer k assumir todos os
números naturais possíveis. Para obter os múltiplos de 2, isto é, os
números da forma a=k×2 onde k é substituído por todos os números
naturais possíveis. A tabela abaixo nos auxiliará:
0=0×2, 2=1×2, 4=2×2, 6=3×2, 8=4×2, 10=5×2, 12=6×2
O conjunto dos números naturais é infinito, assim existem infinitos
múltiplos para qualquer número natural. Se y é um número natural,
o conjunto de todos os múltiplos de y, será denotado por M(y). Por
exemplo:
M(7)={ 0, 7, 14, 21, 28, 35, 42, ... }
M(11)={ 0, 11, 22, 33, 44, 55, 66, 77, ... }
Observação: Como estamos considerando 0 como um número
natural, então o zero será múltiplo de todo número natural.
Tomando k=0 em a=k.b obtemos a=0 para todo b natural. Por
exemplo:
0=0×2, 0=0×5, 0=0×12, 0=0×15
Observação: Um número b é múltiplo dele mesmo.
a = 1 × b se, e somente se, a=b
Por exemplo, basta tomar o mesmo número multiplicado por 1 para
obter um múltiplo dele próprio, como: 3=1x3, 5=1x5 e 15=1x15.
Divisores de números Naturais
A definição de divisor está relacionada com a de múltiplo. Um
número natural b é divisor do número natural a, se a é múltiplo de b.

60. Exemplo: 3 é divisor de 15, pois 15=3×5, logo 15 é múltiplo de 3 e
também é múltiplo de 5.
Um número natural tem uma quantidade finita de divisores. Por
exemplo, o número 6 poderá ter no máximo 6 divisores, pois
trabalhando no conjunto dos números naturais não podemos dividir
6 por um número maior do que ele.
Os divisores de um número y também formam um conjunto finito,
aqui denotado por D(y).
Exemplos:
(a) Divisores de 6: D(6)={1,2,3,6}
(b) Divisores de 18: D(18)={1,2,3,6,9,18}
(c) Divisores de 15: D(15)={1,3,5,15}
Observação: O número zero é múltiplo de todo número natural e
além disso, zero não divide qualquer número natural, exceto ele
próprio.
Se aceitarmos que 6÷0=b, então teremos que admitir que:
6=0xb
mas não existe um número b que multiplicado por 0 (zero) seja igual
a 6, portanto a divisão de 6 por 0 é impossível.
A divisão de 0/0 (zero por zero) é indeterminada, o que significa que
pode existir uma situação que ela passe a ter significado, no sentido
seguinte:

61. Se aceitarmos que 0÷0=X, então poderemos escrever que:
0÷0=X÷1
Como temos uma igualdade de frações, gerando uma proporção,
deveremos aceitar que o produto dos meios é igual ao produto dos
extremos nesta proporção e assim:
0×1=0×X=0
que não é contraditório e isto pode ser realizado para todo X real,
razão pela qual a expressão da forma 0÷0 é dita indeterminada.
Números primos
Um número primo é um número natural com exatamente dois
divisores naturais distintos.
Exemplos:
(a) 1 não é primo pois D(1)={1}
(b) 2 é primo pois D(2)={1,2}
(c) 3 é primo pois D(3)={1,3}
(d) 5 é primo pois D(5)={1,5}
(e) 7 é primo pois D(7)={1,7}
(f) 14 não é primo pois D(14)={1,2,7,14}
Observação: 1 não é primo pois tem apenas 1 divisor e todo número
natural pode ser escrito como o produto de números primos, de
forma única.

62. Crivo de Eratóstenes
É um processo para obter números primos menores do que um
determinado número natural n. Devemos construir uma tabela
contendo os primeiros n números naturais. Para determinar os
números primos nesta tabela, basta seguir os seguintes passos.
1. Antes de iniciar, lembramos que 1 não é um número primo.
2. Marcamos o número 2, que é o primeiro número primo e
eliminamos todos os múltiplos de 2 que encontrarmos na
tabela.
3. Marcamos o número 3 e eliminamos todos os múltiplos de 3
que encontrarmos na tabela.
4. Determinamos o próximo número primo, que será o próximo
número não marcado da tabela e eliminamos todos os
múltiplos desse número primo que encontrarmos na tabela.
5. Continuamos o processo, sempre voltando ao passo
anterior, com o próximo número primo.
6. Os números que não foram eliminados são os números
primos.
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
Na tabela, listamos os 100 primeiros números naturais, indicando
com a cor mais forte os números primos e com a cor clara os
números que não são primos. Como exemplo, 2 é primo, enquanto
25 não é primo, pois é múltiplo de 5.

63. No quadro abaixo, mostramos os números primos menores do que
100, obtidos pelo crivo de Eratóstenes.
P=
{2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,
89,97}
Mínimo Múltiplo Comum
Diz-se que um número m é múltiplo comum dos número a e b se m
é múltiplo de a e também é múltiplo de b, ou seja.
m=k×a e m=w×b
onde k e w números naturais.
Exemplos: Múltiplos comuns
(a) 24 é múltiplo comum de 6 e 8.
(b) 15 é múltiplo comum de 3 e 5.
Determinaremos agora todos os números que tem 18 como múltiplo
comum, o que é o mesmo que obter todos os divisores naturais de
18.
18 é múltiplo comum de 1 e 18 pois 18=1x18
18 é múltiplo comum de 2 e 9 pois 18=2x9
18 é múltiplo comum de 3 e 6 pois 18=3x6
O número 18 é múltiplo comum de todos os seus divisores, logo:
D(18) = { 1, 2, 3, 6, 9,18 }
Agora obteremos os múltiplos comuns dos números a e b. Para isso
denotaremos por M(a) o conjunto dos múltiplos de a, por M(b) o
conjunto dos múltiplos de b e tomaremos a interseção entre os
conjuntos M(a) e M(b).

64. Exemplo: Múltiplos comuns de 3 e 5.
M(3)={0,3,6,9,12,15,18,21,24,27,30,33,36,39,42,45,...}
M(5)={0,5,10,15,20,25,30,35,40,45,50,55,...}
M(3) M(5)={0,15,30,45,...}
Como estamos considerando 0 (zero) como número natural, ele irá
fazer parte dos conjuntos de todos os múltiplos de números naturais
e será sempre o menor múltiplo comum, mas por definição, o
Mínimo Múltiplo Comum (MMC) de dois ou mais números naturais é
o menor múltiplo comum a esses números que é diferente de zero.
Logo, no conjunto:
M(3) M(5)={0, 15, 30, 45, ...}
o Mínimo Múltiplo Comum entre 3 e 5 é igual a 15.
Ao trabalhar com dois números a e b, utilizamos a notação
MMC(a,b) para representar o Mínimo Múltiplo Comum entre os
números naturais a e b, lembrando sempre que o menor múltiplo
comum deve ser diferente de zero. Por exemplo:
M(4)={0,4,8,12,16,20,24,...}
M(6)={ 0, 6, 12, 18, 24, ...}
MMC(4,6)=min {12,24,36,...}=12
O conjunto dos múltiplos do MMC(a,b) é igual ao conjunto dos
múltiplos comuns de a e b. Por exemplo, se a=3 e b=5:
M(3)={0,3,6,9,12,15,18,21,24,27,30,...}
M(5)={0,5,10,15,20,25,30,35,40,45,...}
M(3) M(5)={0,15,30,45,...}
M(15)={0,15,30,45,60,...}

65. Observe que M(15)=M(3) M(5)
Método prático para obter o MMC
Do ponto de vista didático, o processo acima é excelente para
mostrar o significado do MMC mas existe um método prático para
realizar tal tarefa sem trabalhar com conjuntos.
1. Em um papel faça um traço vertical, de forma que sobre
espaço livre tanto à direita como à esquerda do traço.
|
|
|
2. À esquerda do traço escreva os números naturais como uma
lista, separados por vírgulas, para obter o MMC(a,b,c,...).
Por exemplo, tomaremos 12, 22 e 28 do lado esquerdo do
traço vertical e do lado direito do traço poremos o menor
número primo que divide algum dos números da lista que
está à esquerda. Aqui usamos o 2.
12 22 28 | 2
|
|
3. Dividimos todos os números da lista da esquerda, que são
múltiplos do número primo que está à direita do traço,
criando uma nova lista debaixo da lista anterior com os
valores resultantes das divisões (possíveis) e com os
números que não foram divididos.
12 22 28 | 2

66. 6 11 14 |
|
|
4. Repetimos a partir do passo 3 até que os valores da lista
que está do lado esquerdo do traço se tornem todos iguais a
um.
12 22 28 | 2
6 11 14 | 2
3 11 7 | 3
1 11 7 | 7
1 11 1 | 11
1 1 1 | 924
5. O MMC é o produto dos números primos que colocamos do
lado direito do traço e neste caso: MMC(12,22,28)=924.
Exemplo: Obtemos o MMC dos números 12 e 15, com a tabela:
12 15 |
|
|
e depois dividimos todos os números da lista da esquerda pelos
números primos (quando a divisão for possível), criando novas listas
sob as listas anteriores. O MMC(12,15)=60 é o produto de todos os
números primos que colocamos do lado direito do traço.
12 15 | 2
6 15 | 2
3 15 | 3

67. 1 5 | 5
1 1 | 60
Máximo Divisor Comum
Para obter o Máximo Divisor Comum devemos introduzir o conceito
de divisor comum a vários números naturais. Um número d é divisor
comum de outros dois números naturais a e b se, d divide a e d
divide b simultaneamente. Isto significa que devem existir k1 e k2
naturais tal que:
a = k1 × d e b = k2 × d
Exemplos: Divisores comuns.
(a) 8 divide 24 e 56, pois 24=3x8 e 56=7x8.
(b) 3 divide 15 e 36, pois 15=5x3 e 36=12x3.
Observação: Um número d é divisor de todos os seus múltiplos. O
conjunto dos divisores comuns de dois números é finito, pois o
conjunto dos divisores de um número é finito. O conjunto dos
divisores de um número natural y, será denotado por D(y).
Obteremos agora os divisores comuns aos números 16 e 24, isto é,
obteremos a interseção entre os conjunto D(16) e D(24).
D(16)={ 1, 2, 4, 8, 16 }
D(24)={ 1, 2, 3, 4, 6, 8, 12, 24 }
D(16) D(24)={1, 2, 4, 8}
Ocorre que o menor divisor comum entre os números 16 e 24, é 1,
assim não interessa o menor divisor comum mas sim o maior divisor
que pertence simultaneamente aos dois conjuntos de divisores.

68. Denotaremos por MDC(a,b), o Máximo Divisor Comum entre os
números naturais a e b. Por exemplo, tomemos os conjuntos de
divisores D(16)={1,2,4,8,16} e D(24)={1,2,3,4,6,8,12,24}, então:
MDC(16,24)=max( D(16) D(24))=8
Método prático para obter o MDC
De forma similar ao cálculo do MMC(a,b), temos também um
procedimento prático para determinar o MDC(a,b) entre dois
números naturais, pois encontrar conjuntos de divisores para cada
número pode ser trabalhoso. Para introduzir este método,
determinaremos o MDC entre os números 30 e 72, a título de
exemplo.
1. Construímos uma grade com 3 linhas e algumas colunas,
pondo os números dados na linha do meio. Na primeira
coluna coloque o maior deles e na segunda coluna o menor.
72 30
2. Realizamos a divisão do maior pelo menor colocando o
quociente no espaço sobre o número menor na primeira
linha e o resto da divisão no espaço logo abaixo do maior
número na terceira linha.
2
72 30
12
3. Passamos o resto da divisão para o espaço localizado à
direita do menor número na linha central.

69. 2
72 30 12
12
4. Realizamos agora a divisão do número 30, pelo resto obtido
anteriormente que é 12. Novamente, o quociente será
colocado sobre o número 12 e o resto da divisão ficará
localizado abaixo do número 30.
2 2
72 30 12
12 6
5. Realizamos agora a (última!) divisão do número 12, pelo
resto obtido anteriormente que é 6. De novo, o quociente
será posto sobre o número 6 e o resto da divisão ficará
localizado abaixo do número 12.
2 2 2
72 30 12 6
12 6 0
6. Como o resto da última divisão é 0 (zero), o último quociente
obtido representa o MDC entre 30 e 72, logo denotamos tal
fato por:
MDC(30,72) = 6
Exercícios:

70. a. Se a diferença entre dois números naturais é 126 e o
máximo divisor comum entre eles é 18, quais são esses
números?
Solução: Se X e Y são os números procurados, eles devem
ser múltiplos de 18 e podem ser escritos na forma X=18a e
Y=18b onde a e b devem ser determinados. Assim: 18a-
18b=126, de onde segue que 18(a-b)=18×7, o que é
equivalente a: a-b=7. Tomando a=8 e b=1 teremos X=144 e
Y=18.
b. Se a soma de dois números naturais é 420 e o máximo
divisor comum entre eles é 60, quais são esses números?
Solução: Sejam X e Y os números procurados. Se
MDC(X,Y)=60, os números X e Y devem ser múltiplos de 60,
logo podem ser escritos na forma X=60a e Y=60b onde a e b
são números inteiros positivos. Assim: 60a+60b=420, o que
garante que a+b=7. Devemos escolher números naturais tal
que a+b=7, e assim, temos várias opções.
Se a=6 e b=1 então X=360 e Y= 60
Se a=5 e b=2 então X=300 e Y=120
Se a=4 e b=3 então X=240 e Y=180
Se a=3 e b=4 então X=180 e Y=240
Se a=2 e b=5 então X=120 e Y=300
Se a=1 e b=6 então X= 60 e Y=360
c. Se a divisão entre dois números naturais é igual a 6/5 e o
máximo divisor comum entre eles é 15, quais são esses
números?
Solução: Sejam X e Y os números procurados. Se
MDC(X,Y)=15, então X e Y devem ser múltiplos de 15, logo
podem ser escritos na forma X=15a e Y=15b. Assim:

71. (15a)/(15b)=6/5, logo a/b=6/5. Algumas soluções para o
problema, são:
Se a= 6 e b= 5 então X= 90 e Y= 75
Se a=12 e b=10 então X=180 e Y=150
Se a=18 e b=15 então X=270 e Y=225
Relação entre o MMC e MDC
Uma relação importante e bastante útil entre o MMC e o MDC é o
fato que o MDC(a,b) multiplicado pelo MMC(a,b) é igual ao produto
de a por b, isto é:
MDC(a,b) × MMC(a,b) = a × b
MDC(12,15) × MMC(12,15)=12 × 15
Esta relação é útil quando precisamos obter o MMC e o MDC de
dois números, basta encontrar um deles e usar a relação acima.
Exemplo: Para obter o MMC(15,20) e o MDC(15,20), o primeiro
passo é obter o que for possível. Se MDC(15,20)=5 e 15 x 20=300,
basta lembrar que MDC(15,20)×MMC(15,20)=15×20 e fazer:
5 × MMC(15,20) = 300
de onde se obtém que MMC(15,20)=60.
Exercício: Se a soma de dois números é 320 e o mínimo múltiplo
comum entre eles é 600, quais são esses números? Qual é o
máximo divisor comum entre eles?
Solução: Se X e Y são os números procurados, eles devem ser
divisores de 600, logo devem pertencer ao conjunto D(600):

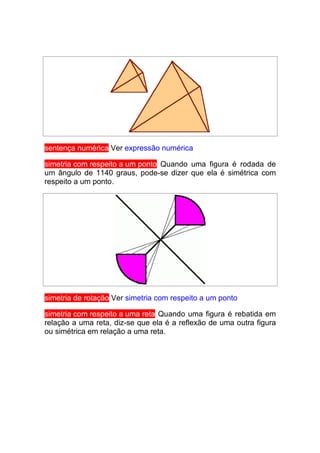
72. {1,2,3,4,5,6,8,10,12,15,20,24,25,30,75,100,120,150,200,300,600}
Pares de números deste conjunto que somam 320, são: 300 e 20 ou
200 e 120. O primeiro par não serve pois MMC(300,20)=300. Os
números que servem são X=200 e Y=120 pois MMC(200,120)=600
e MDC(200,120)=40.
Primos entre si
Dois números naturais são primos entre si quando o MDC entre eles
é igual a 1. Por exemplo, 16 não é um número primo, 21 também
não é um número primo mas 16 e 21 são primos entre si pois
MDC(16,21)=1.
Radiciação de números naturais
Radiciação de ordem n é o processo pelo qual dado um número
natural a devemos determinar um número natural b tal que:
bn = a
onde n é um número natural. É o processo inverso da potenciação.
Neste trabalho, representaremos a operação de radiciação por
Rn[a], a1/n, pot(a,1/n), pow(a,1/n),
que se lê: raiz n-ésima de a. Uma notação simples e muito comum
no meio científico é aquela que usa o acento circunflexo: a^(1/n).
Raiz quadrada: A raiz quadrada de um número não negativo (não
somente natural) é um outro número não negativo b tal que:
b2 = a

73. A raiz quadrada de um número a>0 pode ser denotada por a1/2.
Exemplo: Para obter a raiz quadrada de 36 deve-se obter o valor
numérico de b de forma que:
b2 = b × b = 36
Neste trabalho, usaremos o processo de tentativa, para dividir 36
por seus divisores até que o divisor seja igual ao quociente
36÷2=18, 36÷3=12, 36÷4=9, 36÷6=6
Portanto 6 é a raiz quadrada de 36.
Raiz cúbica: A raiz cúbica de um número (não somente natural) a é
um número b tal que:
b3 = b . b . b = a
A raiz cúbica de um número a pode ser denotada por a1/3.
Exemplo: Para determinar a raiz cúbica de 64, deve-se obter um
número b de forma a obter
b3=b×b×b=64
Por tentativa, temos:
1×1×1=1, 2×2×2=8, 3×3×3=27, 4×4×4=64
Portanto 4 é raiz cúbica de 64.

74. Em estudos mais avançados, pode-se aprender a extrair a raiz
quadrada ou a raiz cúbica de um número não necessariamente
natural, com qualquer precisão que se queira.
5- Ensino Fundamental: Critérios de Divisibilidade
Divisibilidade por Divisibilidade por Divisibilidade por
5 10 19
Sobre a Divisibilidade por Divisibilidade por Divisibilidade por
divisibilidade 6 11 23
Divisibilidade por 2 Divisibilidade por Divisibilidade por Divisibilidade por
7 13 29
Divisibilidade por 3
Divisibilidade por Divisibilidade por Divisibilidade por
Divisibilidade por 4 8 16 31
Divisibilidade por Divisibilidade por Divisibilidade por
9 17 49
Sobre a divisibilidade
Em algumas situações precisamos apenas saber se um número
natural é divisível por outro número natural, sem a necessidade de
obter o resultado da divisão. Neste caso utilizamos as regras
conhecidas como critérios de divisibilidade. Apresentamos as regras
de divisibilidade por 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 16, 17, 19, 23,
29, 31 e 49.
Alguns critérios de divisibilidade
Divisibilidade por 2
Um número é divisível por 2 se ele é par, ou seja, termina em 0, 2,
4, 6 ou 8.

75. Exemplos: O número 5634 é divisível por 2, pois o seu último
algarismo é 4, mas 135 não é divisível por 2, pois é um número
terminado com o algarismo 5 que não é par.
Divisibilidade por 3
Um número é divisível por 3 se a soma de seus algarismos é
divisível por 3.
Exemplos: 18 é divisível por 3 pois 1+8=9 que é divisível por 3, 576
é divisível por 3 pois: 5+7+6=18 que é divisível por 3, mas 134 não
é divisível por 3, pois 1+3+4=8 que não é divisível por 3.
Divisibilidade por 4
Um número é divisível por 4 se o número formado pelos seus dois
últimos algarismos é divisível por 4.
Exemplos: 4312 é divisível por 4, pois 12 é divisível por 4, mas 1635
não é divisível por 4 pois 35 não é divisível por 4.
Divisibilidade por 5
Um número é divisível por 5 se o seu último algarismo é 0 (zero) ou
5.
Exemplos: 75 é divisível por 5 pois termina com o algarismo 5, mas
107 não é divisível por 5 pois o seu último algarismo não é 0 (zero)
nem 5.
Divisibilidade por 6

76. Um número é divisível por 6 se é par e a soma de seus algarismos é
divisível por 3.
Exemplos: 756 é divisível por 6, pois 756 é par e a soma de seus
algarismos: 7+5+6=18 é divisível por 3, 527 não é divisível por 6,
pois não é par e 872 é par mas não é divisível por 6 pois a soma de
seus algarismos: 8+7+2=17 não é divisível por 3.
Divisibilidade por 7
Um número é divisível por 7 se o dobro do último algarismo,
subtraído do número sem o último algarismo, resultar um número
divisível por 7. Se o número obtido ainda for grande, repete-se o
processo até que se possa verificar a divisão por 7.
Exemplo: 165928 é divisível por 7 pois:
16592 Número sem o último algarismo
-16 Dobro de 8 (último algarismo)
16576 Diferença
Repete-se o processo com este último número.
1657 Número sem o último algarismo
-12 Dobro de 6 (último algarismo)
1645 Diferença
Repete-se o processo com este último número.
164 Número sem o último algarismo
-10 Dobro de 5 (último algarismo)
154 Diferença
Repete-se o processo com este último número.
15 Número sem o último algarismo

77. -8 Dobro de 4 (último algarismo)
7 Diferença
A diferença é divisível por 7, logo o número dado inicialmente
também é divisível por 7.
Exemplo: 4261 não é divisível por 7, pois:
426 Número sem o último algarismo
-2 Dobro do último algarismo
424 Diferença
Repete-se o processo com este último número.
42 Número sem o último algarismo
-8 Dobro do último algarismo
34 Diferença
A última diferença é 34 que não é divisível por 7, logo o número
4261 dado inicialmente não é divisível por 7.
Divisibilidade por 8
Um número é divisível por 8 se o número formado pelos seus três
últimos algarismos é divisível por 8.
Exemplos: 45128 é divisível por 8 pois 128 dividido por 8 fornece
16, mas 45321 não é divisível por 8 pois 321 não é divisível por 8.
Divisibilidade por 9
Um número é divisível por 9 se a soma dos seus algarismos é um
número divisível por 9.

78. Exemplos: 1935 é divisível por 9 pois: 1+9+3+5=18 que é divisível
por 9, mas 5381 não é divisível por 9 pois: 5+3+8+1=17 que não é
divisível por 9.
Divisibilidade por 10
Um número é divisível por 10 se termina com o algarismo 0 (zero).
Exemplos: 5420 é divisível por 10 pois termina em 0 (zero), mas
6342 não termina em 0 (zero).
Divisibilidade por 11
Um número é divisível por 11 se a soma dos algarismos de ordem
par Sp menos a soma dos algarismos de ordem ímpar Si é um
número divisível por 11. Como um caso particular, se Sp-Si=0 ou se
Si-Sp=0, então o número é divisível por 11.
Exemplo: 1353 é divisível por 11, pois:
Número 1 3 5 3
Ordem ímpar par ímpar par
O primeiro e o terceiro algarismos têm ordem impar e a sua soma é:
Si=1+5=6, o segundo e o quarto algarismos têm ordem par e a sua
soma é: Sp=3+3=6, assim a soma dos algarismos de ordem par Sp
é igual à soma dos algarismos de ordem ímpar Si, logo o número é
divisível por 11.
Exemplo: 29458 é divisível por 11, pois:
Número 2 9 4 5 8

79. Ordem ímpar par ímpar par ímpar
A soma dos algarismos de ordem ímpar, Si=2+4+8=14, a soma dos
algarismos de ordem par, Sp=9+5=14 e como ambas as somas são
iguais, o número 29458 é divisível por 11.
Exemplo: 2543 não é divisível por 11, pois:
Número 2 5 4 3
Ordem ímpar par ímpar par
A soma dos algarismos de ordem impar é Si=2+4=6, a soma dos
algarismos e ordem par é Sp=5+3=8 e como a diferença Si-Sp não
é divisível por 11, o número original também não é divisível por 11.
Exemplo: 65208 é divisível por 11, pois:
Número 6 5 2 0 8
Ordem ímpar par ímpar par ímpar
A soma dos algarismos de ordem impar é Si=6+2+8=16, a soma
dos algarismos de ordem par é Sp=5+0=5. Como a diferença Si-
Sp=11, o número 65208 é divisível por 11
Divisibilidade por 13
Um número é divisível por 13 se o quádruplo (4 vezes) do último
algarismo, somado ao número sem o último algarismo, resultar um
número divisível por 13. Se o número obtido ainda for grande,
repete-se o processo até que se possa verificar a divisão por 13.
Este critério é semelhante àquele dado antes para a divisibilidade
por 7, apenas que no presente caso utilizamos a soma ao invés de
subtração.

80. Exemplo: 16562 é divisível por 13? Vamos verificar.
1656 Número sem o último algarismo
+8 Quatro vezes o último algarismo
1664 Soma
Repete-se o processo com este último número.
166 Número sem o último algarismo
+16 Quatro vezes o último algarismo
182 Soma
Repete-se o processo com este último número.
18 Número sem o último algarismo
+8 Quatro vezes o último algarismo
26 Soma
Como a última soma é divisível por 13, então o número dado
inicialmente também é divisível por 13.
Divisibilidade por 16
Um número é divisível por 16 se o número formado pelos seus
quatro últimos algarismos é divisível por 16.
Exemplos: 54096 é divisível por 16 pois 4096 dividido por 16
fornece 256, mas 45321 não é divisível por 16 pois 5321 não é
divisível por 16.
Divisibilidade por 17

81. Um número é divisível por 17 quando o quíntuplo (5 vezes) do
último algarismo, subtraído do número que não contém este último
algarismo, proporcionar um número divisível por 17. Se o número
obtido ainda for grande, repete-se o processo até que se possa
verificar a divisão por 17.
Exemplo: 18598 é divisível por 17 pois:
1859 Número sem o último algarismo
-40 Cinco vezes o último algarismo
1819 Diferença
Repete-se o processo com este último número.
181 Número sem o último algarismo
-45 Cinco vezes o último algarismo
136 Diferença
Repete-se o processo com este último número.
13 Número sem o último algarismo
-30 Cinco vezes o último algarismo
-17 Diferença
A diferença, embora negativa, é divisível por 17, logo o número
dado inicialmente também é divisível por 17.
Divisibilidade por 19
Um número é divisível por 19 quando o dobro do último algarismo,
somado ao número que não contém este último algarismo,
proporcionar um número divisível por 19. Se o número obtido ainda
for grande, repete-se o processo até que se possa verificar a divisão
por 19.

82. Exemplo: 165928 é divisível por 19? Vamos verificar.
16592 Número sem o último algarismo
+16 Dobro do último algarismo
16608 Soma
Repete-se o processo com este último número.
1660 Número sem o último algarismo
+16 Dobro do último algarismo
1676 Soma
Repete-se o processo com este último número.
167 Número sem o último algarismo
+12 Dobro do último algarismo
179 Soma
Repete-se o processo com este último número.
17 Número sem o último algarismo
+18 Dobro do último algarismo
35 Soma
Como a última soma não é divisível por 19, então o número dado
inicialmente também não é divisível por 19.
Exemplo: 4275 é divisível por 19, pois:
427 Número sem o último algarismo
+10 Dobro do último algarismo
437 Soma
Repete-se o processo com este último número.

83. 43 Número sem o último algarismo
+14 Dobro do último algarismo
57 Soma
Repete-se o processo com este último número.
5 Número sem o último algarismo
+14 Dobro do último algarismo
19 Soma
Como a última Soma é o próprio 19, segue que é divisível por 19,
então o número 4275 dado inicialmente é divisível por 19.
Divisibilidade por 23
Um número é divisível por 23 quando o héptuplo (7 vezes) do último
algarismo, somado ao número que não contém este último
algarismo, proporcionar um número divisível por 23. Se o número
obtido ainda for grande, repete-se o processo até que se possa
verificar a divisão por 23.
Exemplo: 185909 é divisível por 23? Vamos verificar.
18590 Número sem o último algarismo
+63 Dobro do último algarismo
18653 Soma
Repete-se o processo com este último número.
1865 Número sem o último algarismo
+21 Dobro do último algarismo
1886 Soma
Repete-se o processo com este último número.

84. 188 Número sem o último algarismo
+42 Dobro do último algarismo
230 Soma
Como a última soma é divisível por 23, então o número dado
inicialmente também é divisível por 23.
Divisibilidade por 29
Um número é divisível por 29 quando o triplo (3 vezes) do último
algarismo, subtraído do número que não contém este último
algarismo, proporcionar um número divisível por 29. Se o número
obtido ainda for grande, repete-se o processo até que se possa
verificar a divisão por 29.
Exemplo: O número 8598 é divisível por 29?
859 Número sem o último algarismo
-24 Dobro do último algarismo
835 Diferença
Repete-se o processo com este último número.
83 Número sem o último algarismo
-15 Dobro do último algarismo
68 Diferença
Repete-se o processo com este último número.
6 Número sem o último algarismo
-24 Dobro do último algarismo
-18 Diferença

85. A diferença, embora negativa, não é divisível por 29, logo o número
dado inicialmente também não é divisível por 29.
Divisibilidade por 31
Um número é divisível por 31 quando o triplo (3 vezes) do último
algarismo, somado ao número que não contém este último
algarismo, proporcionar um número divisível por 31. Se o número
obtido ainda for grande, repete-se o processo até que se possa
verificar a divisão por 31.
Exemplo: 8598 é divisível por 31?
859 Número sem o último algarismo
+24 Triplo do último algarismo
883 Soma
Repete-se o processo com este último número.
88 Número sem o último algarismo
+9 Triplo do último algarismo
97 Soma
Repete-se o processo com este último número.
9 Número sem o último algarismo
+21 Triplo do último algarismo
30 Soma
A soma não é divisível por 31, logo o número dado inicialmente
também não é divisível por 31.
Divisibilidade por 49

86. Um número é divisível por 49 quando o quíntuplo (5 vezes) do
último algarismo, somado ao número que não contém este último
algarismo, proporcionar um número divisível por 49. Se o número
obtido ainda for grande, repete-se o processo até que se possa
verificar a divisão por 49.
Exemplo: 8598 é divisível por 49?
859 Número sem o último algarismo
+40 Cinco vezes o último algarismo
899 Soma
Repete-se o processo com este último número.
89 Número sem o último algarismo
+45 Cinco vezes o último algarismo
134 Soma
Repete-se o processo com este último número.
13 Número sem o último algarismo
+20 Cinco vezes o último algarismo
33 Soma
A soma não é divisível por 49, logo o número dado inicialmente
também não é divisível por 49.
6- Ensino Fundamental: Exercícios Resolvidos de MDC, MMC e
Divisores
R[n] = raiz quadrada de z (z>0) e R³[z] = raiz cúbica de z.

87. 1. Um conjunto possui 18 elementos. Quais as possibilidades
existentes para se dividir esse conjunto em grupos com
quantidades iguais de elementos?
Resposta: As possibilidades estão apresentadas na tabela
abaixo:
1 grupo com 18 elementos
2 grupos com 9 elementos em cada grupo
3 grupos com 6 elementos em cada grupo
6 grupos com 3 elementos em cada grupo
9 grupos com 2 elementos em cada grupo
18 grupos com 1 elemento em cada grupo
O conjunto dos divisores de 18 é D(18)={1,2,3,6,9,18}.
2. De que forma explícita podemos escrever o conjunto de
todos os múltiplos de um número natural n?
Resposta: O conjunto dos números naturais é
N={0,1,2,3,4,5,...}. Se n é um número para o qual queremos
obter os múltiplos, então a multiplicação de n por cada
elemento de N será: M(n)={0,n,2n,3n,4n,...}.

88. 3. Quantos elementos possui e como é escrito o conjunto dos
múltiplos do elemento 0?
Resposta: O conjunto de múltiplos de 0 possui apenas um
elemento e é denotado por M(0)={0}, pois
M(0)={0x0,0x1,0x2,0x3,0x4,0x5,...}.
4. Maria possui 3 tias. No aniversário de Maria, ela recebeu 2
presentes de cada tia. Quantos presentes Maria ganhou no
total?
Resposta: No total, Maria ganhou 6 presentes.
5. Para obter os divisores de um número natural a, basta saber
quais os elementos que, multiplicados entre si, têm por
resultado o número a. Com base nessa afirmação, obtenha
o conjunto de divisores de cada um dos números: 13, 18. 25,
32 e 60.
Resposta: D(13)={1,13}, D(18)={1,2,3,6,9,18},
D(25)={1,5,25}, D(60)={1,2,3,4,5,6,10,12,15,20,30,60} e
D(32)={1,2,4,8,16,32}. Obtivemos apenas alguns números
naturais que, multiplicados entre si, têm por resultado 32:
1×32=32; 2×16=32; 4×8=32, 8×4=32, 16×2=32, 32×1=32.
6. Qual o elemento do conjunto dos números naturais que é
divisor de todos os números?
Resposta: O número 1, pois se dividirmos um número
natural n por 1 obteremos o próprio n. Por exemplo, 2 maçãs
para 1 garoto, 3 balas para 1 criança, 5 lápis para 1
estudante, etc...

89. 7. João tinha 20 bolinhas de gude e queria distribuí-las entre
ele e 3 amigos de modo que cada um ficasse com um
número par de bolinhas e nenhum deles ficasse com o
mesmo número que o outro. Com quantas bolinhas ficou
cada menino?
Resposta: Se o primeiro menino ficar com 2 bolinhas,
sobrarão 18 bolinhas para os outros 3 meninos. Se o
segundo receber 4, sobrarão 14 bolinhas para os outros dois
meninos. O terceiro menino receberá 6 bolinhas e o quarto
receberá 8 bolinhas.
8. Quando possível, complete o espaço entre parênteses com
números naturais.
9. 5×( ) = 20
10. ( )×3 = 18
11. 4×( ) = 10
12. ( )÷2 = 8
13. 3÷( ) = 4
14. ( )÷3 = 4
Resposta: Não existe número natural que multiplicado por 4
produza 10 e não existe número natural que divide o número
3 e tem por resultado o número 4.
15. O número 5 é divisor do número 16? Justifique a sua
resposta.
Resposta: Não, porque não existe qualquer número natural
que multiplicado por 5 seja igual a 16.

90. 16. Na Páscoa, um comerciante de Ovos de Páscoa fez a
seguinte promoção:
17. 1 ovo = R$ 6,00
18. 2 ovos = R$ 11,00
19. 3 ovos = R$ 15,00
20. 4 ovos = R$ 18,00
Um cliente realizou uma compra sob certas circunstâncias.
Quantos ele pagou pela compra de 11 ovos?
Quantos ele pagaria se comprasse 177 ovos?
Sem promoção, quanto ele pagaria
a mais pela compra dos 177 ovos?
Resposta: Para comprar 11 ovos ele dividiu 11 por 4 para
obter o maior número múltiplo de 4 e o resto da divisão será
3, assim ele usou a decomposição: 11=4+4+3.
Custo=R$18,00+R$18,00+R$15,00=R$51,00.
Para comprar 177 ovos, ele deve dividir 177 por 4 para obter
o maior número múltiplo de 4 e o resto da divisão será 1,
assim: 177=4×44+1
Custo=44×R$18,00+R$6,00=R$798,00.
21. Conhecendo um método para identificar os números
primos, verifique quais dos seguintes números são primos:
22. (a) 49
23. (b) 37
24. (c) 12

91. 25. (d) 11
Resposta: 37 e 11 são primos porque seus únicos divisores
são o número 1 e eles mesmos. 49 não é primo porque é
múltiplo de 7. 12 não é primo porque é múltiplo de 2, 3, 4 e
6.
26. Qual é o menor número primo com dois algarismos?
Resposta: O número 11.
27. Qual é o menor número primo com dois algarismos
diferentes?
Resposta: O número 13.
28. Qual é o menor número primo com três algarismos
diferentes?
Resposta: O número 103.
29. Qual é o valor do número natural b, tal que 64=b×b×b?
Resposta: R³[64]=4, pois 64=b×b×b, ou seja, 64=b³. Esta é
uma propriedade de potenciação. A base é b e o expoente é
3. O número que elevado ao cubo fornece o resultado 64 é o
número b=4.
30. Tente obter justificativas para garantir que valem as
igualdades com potências e radicais.

92. R[9]=3 2³=8 R³[8]=2 R[16]=4 5²=25
31. Exiba todos os números primos existentes entre 10 e
20?
Resposta: 11, 13, 17 e 19.
32. Escreva três números diferentes cujos únicos fatores
primos são os números 2 e 3.
Resposta: 18, 12, ... A resposta pode ser muito variada.
Alguns exemplos estão na justificativa abaixo. Para
obtermos números que possuem apenas os números 2 e 3
como fatores, não precisamos escolher um número e fatorá-
lo. O meio mais rápido de encontrar um número que possui
por únicos fatores os números 2 e 3 é "criá-lo" multiplicando
2 e 3 quantas vezes desejarmos. Por exemplo: 2×2×3=12,
3×3×2=18, 2×2×3×3×3=108.
33. Seja o quadrado abaixo em que cada lado mede 3cm.
Quantos quadradinhos de 1cm² cabem no quadrado?
34. Resposta: 9 quadradinhos.
35.
36. Com o mesmo quadrado acima, obter o valor de 3².
Resposta: 3²=9.

93. 37. De quantos cubinhos de 1cm de lado, isto é, um
centímetro cúbico, precisaremos para construir um cubo com
3cm de comprimento, 3cm de largura e 3cm de altura?
Resposta: 27 cubinhos.
38. Qual o valor de 33 (3 elevado ao cubo)?
Resposta: 3³=27.
7- Ensino Fundamental: Números Inteiros
Curiosidades com inteiros
Soma de inteiros: Propriedades
Introdução aos números inteiros
Multiplicação de inteiros
Sobre a origem dos sinais
Propriedades da multiplicação
Conjunto Z dos números inteiros
Propriedade mista (distributiva)
A reta numerada
Potenciação de números inteiros
Ordem e simetria no conjunto Z
Radiciação de números inteiros
Módulo de um número inteiro
Adição de números inteiros
Curiosidades com números inteiros
12345679 x 9 = 111111111
12345679 x 18 = 222222222
12345679 x 27 = 333333333
12345679 x 36 = 444444444
12345679 x 45 = 555555555
12345679 x 54 = 666666666

94. 12345679 x 63 = 777777777
12345679 x 72 = 888888888
12345679 x 81 = 999999999
9 x 9 + 7 = 88
9 x 98 + 6 = 888
9 x 987 + 5 = 8888
9 x 9876 + 4 = 88888
9 x 98765 + 3 = 888888
9 x 987654 + 2 = 8888888
9 x 9876543 + 1 = 88888888
9 x 98765432 + 0 = 888888888
9 x 1 + 2 = 11
9 x 12 + 3 = 111
9 x 123 + 4 = 1111
9 x 1234 + 5 = 11111
9 x 12345 + 6 = 111111
9 x 123456 + 7 = 1111111
9 x 1234567 + 8 = 11111111

95. 9 x 12345678 + 9 = 111111111
9 x 123456789 + 10 = 1111111111
11 x 11 = 121
111 x 111 = 12321
1111 x 1111 = 1234321
11111 x 11111 = 123454321
111111 x 111111 = 12345654321
1111111 x 1111111 = 1234567654321
11111111 x 11111111 = 123456787654321
111111111 x 111111111 = 12345678987654321
9 x 7 = 63
99 x 77 = 7623
999 x 777 = 776223
9999 x 7777 = 77762223
99999 x 77777 = 7777622223
999999 x 777777 = 777776222223
9999999 x 7777777 = 77777762222223
99999999 x 77777777 = 7777777622222223

96. 1 x 7 + 3 = 10
14 x 7 + 2 = 100
142 x 7 + 6 = 1000
1428 x 7 + 4 = 10000
14285 x 7 + 5 = 100000
142857 x 7 + 1 = 1000000
1428571 x 7 + 3 = 10000000
14285714 x 7 + 2 = 100000000
142857142 x 7 + 6 = 1000000000
1428571428 x 7 + 4 = 10000000000
14285714285 x 7 + 5 = 100000000000
142857142857 x 7 + 1 = 1000000000000
9 x 9 = 81
99 x 99 = 9801
999 x 999 = 998001
9999 x 9999 = 99980001
99999 x 99999 = 9999800001
999999 x 999999 = 999998000001

97. 12 x 12 = 144, 21 x 21 = 441
13 x 13 = 169, 31 x 31 = 961
102x102 = 10404, 201x201 = 40401
103x103 = 10609, 301x301 = 90601
112x112 = 12544, 211x211 = 44521
122x122 = 14884, 221x221 = 48841
99 = 9+8+7+65+4+3+2+1
100 = 1+2+3+4+5+6+7+8×9
134498697 = 1 + 2^3 + 4^5 + 6^7 + 8^9
1000 = 8 + 8 + 8 + 88 + 888
45 = 8+12+5+20, 8+2=12-2=5x2=20÷2=10
100 = 12+20+4+64, 12+4=20-4=4x4=64÷4=16
225 = 1+23+45+67+89, 89-67=67-45=45-23=23-1=22
5^2 + 2^1 = (5-2)^(2+1)
Notação: Para indicar que um número x está elevado a y, escreverei
x^y, que é uma notação comum no meio científico.

98. Introdução aos números inteiros
Na época do Renascimento, os matemáticos sentiram cada vez
mais a necessidade de um novo tipo de número, que pudesse ser a
solução de equações tão simples como:
x + 2 = 0, 2x + 10 = 0, 4y + 4 = 0
As Ciências precisavam de símbolos para representar temperaturas
acima e abaixo de 0º C, por exemplo. Astrônomos e físicos
procuravam uma linguagem matemática para expressar a atração
entre dois corpos.
Quando um corpo age com uma força sobre outro corpo, este reage
com uma força de mesma intensidade e sentido contrário. Mas a
tarefa não ficava somente em criar um novo número, era preciso
encontrar um símbolo que permitisse operar com esse número
criado, de modo prático e eficiente.
Sobre a origem dos sinais
A idéia sobre os sinais vem dos comerciantes da época. Os
matemáticos encontraram a melhor notação para expressar esse
novo tipo de número. Veja como faziam tais comerciantes:
Suponha que um deles tivesse em seu armazém duas sacas de
feijão com 10 kg cada. Se esse comerciante vendesse num dia 8 Kg
de feijão, ele escrevia o número 8 com um traço (semelhante ao
atual sinal de menos) na frente para não se esquecer de que no
saco faltava 8 Kg de feijão.
Mas se ele resolvesse despejar no outro saco os 2 Kg que restaram,
escrevia o número 2 com dois traços cruzados (semelhante ao atual

99. sinal de mais) na frente, para se lembrar de que no saco havia 2 Kg
de feijão a mais que a quantidade inicial.
Com essa nova notação,os matemáticos poderiam, não somente
indicar as quantidades, mas também representar o ganho ou a
perda dessas quantidades, através de números, com sinal positivo
ou negativo.
O conjunto Z dos Números Inteiros
Definimos o conjunto dos números inteiros como a reunião do
conjunto dos números naturais, o conjunto dos opostos dos
números naturais e o zero. Este conjunto é denotado pela letra Z
(Zahlen=número em alemão). Este conjunto pode ser escrito por:
Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4,...}
Exemplos de subconjuntos do conjunto Z
(a) Conjunto dos números inteiros excluído o número zero:
Z* = {..., -4, -3, -2, -1, 1, 2, 3, 4,...}
(b) Conjunto dos números inteiros não negativos:
Z+ = {0, 1, 2, 3, 4,...}
(c) Conjunto dos números inteiros não positivos:
Z- = {..., -4, -3, -2, -1, 0}
Observação: Não existe padronização para estas notações.
Reta Numerada
Uma forma de representar geometricamente o conjunto Z é construir
uma reta numerada, considerar o número 0 como a origem e o

100. número 1 em algum lugar, tomar a unidade de medida como a
distância entre 0 e 1 e por os números inteiros da seguinte maneira:
Ao observar a reta numerada notamos que a ordem que os números
inteiros obedecem é crescente da esquerda para a direita, razão
pela qual indicamos com uma seta para a direita. Esta consideração
é adotada por convenção, o que nos permite pensar que se fosse
adotada outra forma, não haveria qualquer problema.
Baseando-se ainda na reta numerada podemos afirmar que todos
os números inteiros possuem um e somente um antecessor e
também um e somente um sucessor.
Ordem e simetria no conjunto Z
O sucessor de um número inteiro é o número que está
imediatamente à sua direita na reta (em Z) e o antecessor de um
número inteiro é o número que está imediatamente à sua esquerda
na reta (em Z).
Exemplos:
(a) 3 é sucessor de 2
(b) 2 é antecessor de 3
(c) -5 é antecessor de -4
(d) -4 é sucessor de -5
(e) 0 é antecessor de 1
(f) 1 é sucessor de 0
(g) -1 é sucessor de -2

101. (h) -2 é antecessor de -1
Todo número inteiro exceto o zero, possui um elemento
denominado simétrico ou oposto -z e ele é caracterizado pelo fato
geométrico que tanto z como -z estão à mesma distância da origem
do conjunto Z que é 0.
Exemplos:
(a) O oposto de ganhar é perder, logo o oposto de
+3 é -3.
(b) O oposto de perder é ganhar, logo o oposto de
-5 é +5.
Módulo de um número Inteiro
O módulo ou valor absoluto de um número Inteiro é definido como
sendo o maior valor (máximo) entre um número e seu elemento
oposto e pode ser denotado pelo uso de duas barras verticais | |.
Assim:
|x| = max{-x,x}
Exemplos:
(a) |0| = 0
(b) |8| = 8
(c) |-6| = 6
Observação: Do ponto de vista geométrico, o módulo de um número
inteiro corresponde à distância deste número até a origem (zero) na
reta numérica inteira.
Soma (adição) de números inteiros

102. Para melhor entendimento desta operação, associaremos aos
números inteiros positivos a idéia de ganhar e aos números inteiros
negativos a idéia de perder.
ganhar 3 + ganhar 4 = ganhar 7 (+3) + (+4) = (+7)
perder 3 + perder 4 = perder 7 (-3) + (-4) = (-7)
ganhar 8 + perder 5 = ganhar 3 (+8) + (-5) = (+3)
perder 8 + ganhar 5 = perder 3 (-8) + (+5) = (-3)
Atenção: O sinal (+) antes do número positivo pode ser dispensado,
mas o sinal (-) antes do número negativo nunca pode ser
dispensado.
Exemplos:
(a) -3 + 3 = 0
(b) +6 + 3 = 9
(c) +5 - 1 = 4
Propriedades da adição de números inteiros
Fecho: O conjunto Z é fechado para a adição, isto é, a soma de dois
números inteiros ainda é um número inteiro.
Associativa: Para todos a,b,c em Z:
a+(b+c)=(a+b)+c
2+(3+7)=(2+3)+7
Comutativa: Para todos a,b em Z:
a+b=b+a
3+7=7+3
Elemento neutro: Existe 0 em Z, que adicionado a cada z em Z,
proporciona o próprio z, isto é:

103. z+0=z
7+0=7
Elemento oposto: Para todo z em Z, existe (-z) em Z, tal que
z + (-z) = 0
9 + (-9) = 0
Multiplicação (produto) de números inteiros
A multiplicação funciona como uma forma simplificada de uma
adição quando os números são repetidos. Poderiamos analisar tal
situação como o fato de estarmos ganhando repetidamente alguma
quantidade, como por exemplo, ganhar 1 objeto por 30 vezes
consectivas, significa ganhar 30 objetos e esta repetição pode ser
indicada por um x, isto é:
1 + 1 + 1 + ... + 1 + 1 = 30 x 1 = 30
Se trocarmos o número 1 pelo número 2, obteremos:
2 + 2 + 2 + ... + 2 + 2 = 30 x 2 = 60
Se trocarmos o número 2 pelo número -2, obteremos:
(-2) + (-2) + ... + (-2) = 30 x (-2) = -60
Observamos que a multiplicação é um caso particular da adição
onde os valores são repetidos.
Na multiplicação o produto dos números a e b, pode ser indicado
por axb, a.b ou ainda ab sem nenhum sinal entre as letras.
Para realizar a multiplicação de números inteiros, devemos
obedecer à seguinte regra de sinais:
(+1) × (+1) = (+1)
(+1) × (-1) = (-1)

104. (-1) × (+1) = (-1)
(-1) × (-1) = (+1)
Com o uso das regras acima, podemos concluir que:
Sinais dos números Resultado do produto
iguais positivo
diferentes negativo
Propriedades da multiplicação de números inteiros
Fecho: O conjunto Z é fechado para a multiplicação, isto é, a
multiplicação de dois números inteiros ainda é um número inteiro.
Associativa: Para todos a,b,c em Z:
ax(bxc)=(axb)xc
2x(3x7)=(2x3)x7
Comutativa: Para todos a,b em Z:
axb=bxa
3x7=7x3
Elemento neutro: Existe 1 em Z, que multiplicado por todo z em Z,
proporciona o próprio z, isto é:
zx1=z
7x1=7
Elemento inverso: Para todo inteiro z diferente de zero, existe um
inverso z-1=1/z em Z, tal que
z x z-1 = z x (1/z) = 1
9 x 9-1 = 9 x (1/9) = 1
Propriedade mista (distributiva)

105. Distributiva: Para todos a,b,c em Z:
ax(b+c)=(axb)+(axc)
3x(4+5)=(3x4)+(3x5)
Potenciação de números inteiros
A potência an do número inteiro a, é definida como um produto de n
fatores iguais. O número a é denominado a base e o número n é o
expoente.
an = a × a × a × a × ... × a
a é multiplicado por a n vezes
Exemplos:
a. 25 = 2 x 2 x 2 x 2 x 2 = 32
b. (-2)³ = (-2) x (-2) x (-2) = -8
c. (-5)² = (-5) x (-5) = 25
d. (+5)² = (+5) x (+5) = 25
com os exemplos acima, podemos observar que a potência de todo
número inteiro elevado a um expoente par é um número positivo e a
potência de todo número inteiro elevado a um expoente ímpar é um
número que conserva o seu sinal.
Observação: Quando o expoente é n=2, a potência a² pode ser lida
como: "a elevado ao quadrado" e quando o expoente é n=3, a
potência a³ pode ser lida como: "a elevado ao cubo". Tais leituras
são provenientes do fato que área do quadrado pode ser obtida por
A=a² onde a é é a medida do lado e o volume do cubo pode ser
obtido por V=a³ onde a é a medida do lado do cubo.
Radiciação de números inteiros
A raiz n-ésima (de ordem n) de um número inteiro a é a operação
que resulta em um outro número inteiro não negativo b que elevado

106. à potência n fornece o número a. O número n é o índice da raiz
enquanto que o número a é o radicando (que fica sob o sinal do
radical). Leia a observação seguinte para entender as razões pelas
quais não uso o símbolo de radical neste trabalho.
Observação: Por deficiência da linguagem HTML, que até hoje não
implementou o sinal de raiz n-ésima, usarei Rn[a] para indicar a raiz
n-ésima de a. Quando n=2, simplesmente indicarei a raiz de ordem
2 de um número inteiro a como R[a].
Assim, b é a raiz n-ésima de a se, e somente se, a=bn, isto é:
b=Rn[a] se, e somente se, a=bn
A raiz quadrada (de ordem 2) de um número inteiro a é a operação
que resulta em um outro número inteiro não negativo que elevado
ao quadrado coincide com o número a.
Observação: Não existe a raiz quadrada de um número inteiro
negativo no conjunto dos números inteiros. A existência de um
número cujo quadrado é igual a um número negativo só será
estudada mais tarde no contexto dos números complexos.
Erro comum: Frequentemente lemos em materiais didáticos e até
mesmo ocorre em algumas aulas aparecimento de:
R[9] = ±3
mas isto está errado. O certo é:
R[9] = +3
Observamos que não existe um número inteiro não negativo que
multiplicado por ele mesmo resulte em um número negativo.

107. A raiz cúbica (de ordem 3) de um número inteiro a é a operação que
resulta em um outro número inteiro que elevado ao cubo seja igual
ao número a. Aqui não restringimos os nossos cálculos somente
aos números não negativos.
Exemplos:
(a) R³[8] = 2, pois 2³ = 8.
(b) R³[-8] = -2, pois (-2)³ = -8.
(c) R³[27] = 3, pois 3³ = 27.
(d) R³[-27] = -3, pois (-3)³ = -27.
Observação: Ao obedecer a regra dos sinais para o produto de
números inteiros, concluímos que:
(a) Se o índice da raiz for par, não existe raiz de número inteiro
negativo.
(b) Se o índice da raiz for ímpar, é possível extrair a raiz de
qualquer número inteiro.
8- Ensino Fundamental: Frações
Histórico sobre frações Propriedades fundamentais
Frações Fração=classe de equivalência
Construindo frações Número misto
Definição de fração Simplificação de frações
Leitura de frações Comparação de frações
Tipos de frações Divisão de frações
Elementos Históricos sobre frações
Há 3000 antes de Cristo, os geômetras dos faraós do Egito
realizavam marcação das terras que ficavam às margens do rio Nilo,

108. para a sua população. Mas, no período de junho a setembro, o rio
inundava essas terras levando parte de suas marcações. Logo os
proprietários das terras tinham que marcá-las novamente e para
isso, eles utilizavam uma marcação com cordas, que seria uma
espécie de medida, denominada estiradores de cordas.
As pessoas utilizavam as cordas, esticando-as e assim verificavam
quantas vezes aquela unidade de medida estava contida nos lados
do terreno, mas raramente a medida dava correta no terreno, isto é,
não cabia um número inteiro de vezes nos lados do terreno; sendo
assim eles sentiram a necessidade de criar um novo tipo de número
- o número fracionário, onde eles utilizavam as frações.
Introdução ao conceito de fração
Às vezes, ao tentar partir algo em pedaços, como por exemplo, uma
pizza, nós a cortamos em partes que não são do mesmo tamanho.
Logo isso daria uma grande confusão, pois quem ficaria com a parte
maior? Ou quem ficaria com a parte menor? É lógico que alguém
sairia no prejuízo.
Pensemos neste exemplo: Dois irmãos foram juntos comprar
chocolate. Eles compraram duas barras de chocolate iguais, uma
para cada um. Iam começar a comer quando chegou uma de suas
melhores amigas e vieram as perguntas: Quem daria um pedaço
para a amiga? Qual deveria ser o tamanho do pedaço? Eles
discutiram e chegaram à seguinte conclusão:
Para que nenhum dos dois comesse menos, cada um daria metade
do chocolate para a amiga.
Você concorda com esta divisão? Por quê?

109. Como você poderia resolver esta situação para que todos
comessem partes iguais?
O que você acha desta frase: Quem parte e reparte e não fica
com a melhor parte, ou é bobo ou não tem arte.
Elementos gerais para a construção de frações
Para representar os elementos que não são tomados como partes
inteiras de alguma coisa, utilizamos o objeto matemático
denominado fração.
O conjunto dos números naturais, algumas vezes inclui o zero e
outras vezes não, tendo em vista que zero foi um número criado
para dar significado nulo a algo. Nesse momento o conjunto N será
representado por:
N = { 1, 2, 3, 4, 5, 6, 7, ... }
Logo, todos os números naturais representam partes inteiras.
Os números que não representam partes inteiras, mas que são
partes de inteiros, constituem os números racionais não-negativos,
aqui representados por Q+, onde esta letra Q significa quociente ou
divisão de dois números inteiros naturais.
Q+ = { 0,..., 1/4,..., 1/2,..., 1,...,2,... }
Numeral: Relativo a número ou indicativo de número.
Número: Palavra ou símbolo que expressa quantidade.
Definição de fração
Os numerais que representam números racionais não-negativos são
chamados frações e os números inteiros utilizados na fração são
chamados numerador e denominador, separados por uma linha
horizontal ou traço de fração.
Numerador

110. Denominador
onde Numerador indica quantas partes são tomadas do inteiro, isto
é, o número inteiro que é escrito sobre o traço de fração e
Denominador indica em quantas partes dividimos o inteiro, sendo
que este número inteiro deve necessariamente ser diferente de
zero.
Observação: A linguagem HTML (para construir páginas da Web)
não proporciona ainda um método simples para a implementar a
barra de fração, razão pela qual, às vezes usaremos a barra / ou
mesmo o sinal ÷, para entender a divisão de dois números.
Exemplo: Consideremos a fração 1/4, que pode ser escrita como:
1
4
Em linguagem matemática, as fracões podem ser escritas tanto
como no exemplo acima ou mesmo como 1/4, considerada mais
comum.
1/4 1/4
1/4 1/4
A unidade foi dividida em quatro partes iguais. A fração pode ser
visualizada através da figura anexada, sendo que foi sombreada
uma dessas partes.
Leitura de frações
(a) O numerador é 1 e o denominador é um inteiro 1<d<10
A leitura de uma fração da forma 1/d, onde d é o denominador que é
menor do que 10 é feita como:

111. Fração 1/2 1/3 1/4 1/5 1/6 1/7 1/8 1/9
um um um um um um um um
Leitura
meio terço quarto quinto sexto sétimo oitavo nono
(b) O numerador é 1 e o denominador é um inteiro d>10
Quando a fração for da forma 1/d, com d maior do que 10, lemos: 1,
o denominador e acrescentamos a palavra avos.
Avos é um substantivo masculino usado na leitura das frações,
designa cada uma das partes iguais em que foi dividida a unidade e
se cujo denominador é maior do que dez.
Fração Leitura
1/11 um onze avos
1/12 um doze avos
1/13 um treze avos
1/14 um quatorze avos
1/15 um quinze avos
1/16 um dezesseis avos
1/17 um dezessete avos
1/18 um dezoito avos
1/19 um dezenove avos
(c) O numerador é 1 e o denominador é um múltiplo de 10
Se o denominador for múltiplo de 10, lemos:
Fração Leitura Leitura Comum
1/10 um dez avos um décimo
1/20 um vinte avos um vigésimo
1/30 um trinta avos um trigésimo
1/40 um quarenta avos um quadragésimo
1/50 um cinqüenta avos um qüinquagésimo
1/60 um sessenta avos um sexagésimo

112. 1/70 um setenta avos um septuagésimo
1/80 um oitenta avos um octogésimo
1/90 um noventa avos um nonagésimo
1/100 um cem avos um centésimo
1/1000 um mil avos um milésimo
1/10000 um dez mil avos um décimo milésimo
1/100000 um cem mil avos um centésimo milésimo
1/1000000 um milhão avos um milionésimo
Observação: A fração 1/3597 pode ser lida como: um, três mil
quinhentos e noventa e sete avos.
Tipos de frações
A representação gráfica mostra a fração 3/4 que é uma fração cujo
numerador é um número natural menor do que o denominador.
1/4 1/4
1/4 1/4
A fração cujo numerador é menor que o denominador, isto é, a parte
é tomada dentro do inteiro, é chamada fração própria. A fração cujo
numerador é maior do que o denominador, isto é, representa mais
do que um inteiro dividido em partes iguais é chamada fração
imprópria.
3/3 2/3 5/3=1+2/3
1/3 1/3 1/3
+ =
1
1/3 1/3 1/3

113. 1/3 1/3 1/3
Fração aparente: é aquela cujo numerador é um múltiplo do
denominador e aparenta ser uma fração mas não é, pois representa
um número inteiro. Como um caso particular, o zero é múltiplo de
todo número inteiro, assim as frações 0/3, 0/8, 0/15 são aparentes,
pois representam o número inteiro zero.
Frações Equivalentes: São as que representam a mesma parte do
inteiro. Se multiplicarmos os termos (numerador e denominador) de
uma fração sucessivamente pelos números naturais, teremos um
conjunto infinito de frações que constitui um conjunto que é
conhecido como a classe de equivalência da fração dada.
1/2 2/4 3/6 4/8
1/2 1/4 1/4 1/6 1/6 1/6 1/8 1/8 1/81/8
1/2 1/4 1/4 1/6 1/6 1/6 1/8 1/8 1/81/8
Propriedades fundamentais
(1) Se multiplicarmos os termos (numerador e denominador) de uma
fração por um mesmo número natural, obteremos uma fração
equivalente à fração dada:
1 1×2 2
= =
2 2×2 4

114. (2) Se é possível dividir os termos (numerador e denominador) de
uma fração por um mesmo número natural, obteremos uma fração
equivalente à fração dada:
12 12÷2 6 6÷2 3
= = = =
16 16÷2 8 8÷2 4
A fração como uma classe de equivalência
A classe de equivalência de uma fração é o conjunto de todas as
frações equivalentes à fração dada. Ao invés de trabalhar com todos
os elementos deste conjunto infinito, simplesmente poderemos
tomar a fração mais simples deste conjunto que será a
representante desta classe. Esta fração será denominada um
número racional. Aplicando a propriedade fundamental, podemos
escrever o conjunto das frações equivalentes a 1/3, como:
C(1/3) = { 1/3, 2/6, 3/9, 4/12, 5/15, 6/18, ... }
Número Misto
Quando o numerador de uma fração é maior que o denominador,
podemos realizar uma operação de decomposição desta fração em
uma parte inteira e uma parte fracionária e o resultado é
denominado número misto.
Transformação de uma fração imprópria em um número misto
17 16+1 16 1 1 1
= = + = 4+ = 4
4 4 4 4 4 4
Transformação de um número misto em uma fração imprópria
4 1 = 4+ 1 = 16 + 1 = 17

115. 4 4 4 4 4
Simplificação de Frações
Simplificar frações é o mesmo que escrevê-la em uma forma mais
simples, para que a mesma se torne mais fácil de ser manipulada.
O objetivo de simplificar uma fração é torná-la uma fração
irredutível, isto é, uma fração para a qual o Máximo Divisor Comum
entre o Numerador e o Denominador seja 1, ou seja, o Numerador e
o Denominador devem ser primos entre si. Essa simplificação pode
ser feita através dos processos de divisão sucessiva e pela
fatoração.
A divisão sucessiva corresponde a dividir os dois termos da fração
por um mesmo número (fator comum ) até que ela se torne
irredutível.
36 36÷2 18 18÷2 9 9÷3 3
= = = = = =
60 60÷2 30 30÷2 15 15÷3 5
Respectivamente, dividimos os termos das frações por 2, 2 e 3.
Observação: Outra maneira de divisão das frações é obter o
Máximo Divisor Comum entre o Numerador e o Denominador e
simplificar a fração diretamente por esse valor.
Exemplo: Simplificaremos a fração 54/72, usando o Máximo Divisor
Comum. Como MDC(54,72)=18, então 54:18=3 e 72:18=4, logo:
54 54÷18 3
= =
72 72÷18 4
Comparação de duas frações
(1) Por redução ao mesmo denominador

116. Se duas frações possuem denominadores iguais, a maior fração é a
que possui maior numerador. Por exemplo:
3 4
<
5 5
(2) Tanto os numeradores como os denominadores das duas
frações são diferentes
Devemos reduzir ambas as frações a um denominador comum e o
processo depende do cálculo do Mínimo Múltiplo Comum entre os
dois denominadores e este será o denominador comum às duas
frações. Na seqüência, divide-se o denominador comum pelo
denominador de cada fração e multiplica-se o resultado obtido pelo
respectivo numerador.
Exemplo: Vamos comparar as frações 2/3 e 3/5. Como os
denominadores são 3 e 5, temos que MMC(3,5)=15. Reduzindo
ambas as frações ao mesmo denominador comum 15, aplica-se a
regra de dividir o denominador comum pelo denominador de cada
fração e na seqüência multiplica-se esse respectivo número pelo
numerador.
2 3
?
3 5
Multiplicando os termos da primeira fração por 5 e multiplicando os
termos da segunda fração por 3, obteremos:
2 2×53×3 3
= ? =
3 3×5 5×3 5
Temos então os mesmos denominadores, logo:
2 10 9 3
= ? =

117. 3 15 15 5
e podemos garantir que
2 10 9 3
= > =
3 15 15 5
(3) As frações possuem um mesmo numerador
Se os numeradores de duas frações forem iguais, será maior a
fração cujo denominador for menor.
Exemplo: Uma representação gráfica para a desigualdade
3 3
>
4 8
pode ser dada geometricamente por:
3/4=6/8 3/8
1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8
1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8
Observe que a área amarelada é maior na primeira figura.
Divisão de frações
Consideremos inicialmente uma divisão D de duas frações,
denotada por:
1 2
D= ÷
2 3

118. Um modo fácil para explicar esta divisão é tomar as duas frações
com o mesmo denominador e realizar a divisão do primeiro
numerador pelo segundo numerador, isto é:
1 2 3 4
D= ÷ = ÷
2 3 6 6
pois 1/2 é equivalente a 3/6 e 2/3 é equivalente a 4/6. O desenho
abaixo mostra as frações 1/2 e 2/3, através de suas respectivas
frações equivalentes: 3/6 e 4/6.
3/6 4/6
1/6 1/6 1/6 1/6 1/6 1/6
1/6 1/6 1/6 1/6 1/6 1/6
Realizar a divisão entre dois números fracionários ou não A e B, é o
mesmo que procurar saber quantas partes de B estão ocupadas por
A. Quantas partes da fração 4/6 estão ocupadas pela fração 3/6?
No desenho, os numeradores das frações estão em cor amarela.
Como temos 3 partes em amarelo na primeira fração e 4 partes em
amarelo na segunda fração, a divisão corresponde à fração 3/4, ou
seja, em cada 4 partes amarelas, 3 estão ocupadas.
Este argumento justifica a divisão de duas frações pela
multiplicação da primeira fração pelo inverso da segunda fração e
observamos que de fato isto funciona neste caso:
1 2 3 6 18 3
D= ÷ = × = =
2 3 6 4 24 4

119. Na verdade, há um tratamento mais geral que o deste caso
particular. A divisão de um número real a/b pelo número real c/d é,
por definição, a multiplicação do número a/b pelo inverso de c/d.
Acontece que o inverso de c/d é a fração d/c, assim:
a c a d a.d
÷ = × =
b d b c b.c
9- Ensino Fundamental: Frações e Números Decimais
O Papel das frações decimais Números decimais -> frações
Elementos históricos Números decimais: Propried.
Frações e Números Decimais Operações com Nos. decimais
Leitura de Números Decimais Comparando números decimais
Frações -> números decimais Porcentagem
O papel das frações e números Decimais
Esta página trata do estudo de frações e números decimais, bem
como seus fatos históricos, propriedades, operações e aplicações.
As frações decimais e números decimais possuem notória
importância cotidiana. Tais conceitos são usados em muitas
situações práticas, embora, muitas vezes passem despercebidas.
Indo ao supermercado comprar 1/2 Kg de café por R$ 2,80 e
pagando a compra com uma nota de R$ 5,00, obtém-se R$ 2,20 de
troco. Neste exemplo, podemos observar o uso de frações e
números decimais. Através deste tipo de compra, usamos o
conceito de fração decimal juntamente com o sistema de pesagem
(1/2 Kg), números decimais juntamente com o sistema monetário.
Muitas outras situações utilizam de frações e números decimais.
Observação: Para dividir um número X por outro número não nulo
Y, usaremos frequentemente a notação X/Y, por ser mais simples.
Elementos históricos sobre os números Decimais

120. Hoje em dia é comum o uso de frações. Houve tempo, porém que
as mesmas não eram conhecidas. O homem introduziu o uso de
frações quando começou a medir e representar medidas.
Os egípcios usavam apenas frações que possuiam o número 1
dividido por um número inteiro, como por exemplo: 1/2, 1/3, 1/4,
1/5,... Tais frações eram denominadas frações egípcias e ainda hoje
têm muitas aplicações práticas. Outras frações foram descobertas
pelos mesmos egípcios as quais eram expressas em termos de
frações egípcias, como: 5/6=1/2+1/3.
Os babilônios usavam em geral frações com denominador 60. É
provável que o uso do número 60 pelos babilônios se deve ao fato
que é um número menor do que 100 com maior quantidade de
divisores inteiros. Os romanos, por sua vez, usavam
constantemente frações com denominador 12. Provavelmente os
romanos usavam o número 12 por ser um número que embora
pequeno, possui um número expressivo de divisores inteiros. Com o
passar dos tempos, muitas notações foram usadas para representar
frações. A atual maneira de representação data do século XVI.
Os números decimais têm origem nas frações decimais. Por
exemplo, a fração 1/2 equivale à fração 5/10 que equivale ao
número decimal 0,5.
Stevin (engenheiro e matemático holandês), em 1585 ensinou um
método para efetuar todas as operações por meio de inteiros, sem o
uso de frações, no qual escrevia os números naturais ordenados em
cima de cada algarismo do numerador indicando a posição ocupada
pela vírgula no numeral decimal. A notação abaixo foi introduzida
por Stevin e adaptada por John Napier, grande matemático
escocês.
1437 123
= 1, 4 3 7
1000

121. A representação dos algarismos decimais, provenientes de frações
decimais, recebia um traço no numerador indicando o número de
zeros existentes no denominador.
437
= 4,37
100
Este método foi aprimorado e em 1617 Napier propôs o uso de um
ponto ou de uma vírgula para separar a parte inteira da parte
decimal.
Por muito tempo os números decimais foram empregados apenas
para cálculos astronômicos em virtude da precisão proporcionada.
Os números decimais simplificaram muito os cálculos e passaram a
ser usados com mais ênfase após a criação do sistema métrico
decimal.
Frações e Números Decimais
Dentre todas as frações, existe um tipo especial cujo denominador é
uma potência de 10. Este tipo é denominado fração decimal.
Exemplos de frações decimais, são:
1/10, 3/100, 23/100, 1/1000, 1/103
Toda fração decimal pode ser representada por um número decimal,
isto é, um número que tem uma parte inteira e uma parte decimal,
separados por uma vírgula.
A fração 127/100 pode ser escrita na forma mais simples, como:
127
= 1,27
100

122. onde 1 representa a parte inteira e 27 representa a parte decimal.
Esta notação subentende que a fração 127/100 pode ser
decomposta na seguinte forma:
127 100+27 100 27
= = + = 1+0,27 = 1,27
100 100 100 100
A fração 8/10 pode ser escrita na forma 0,8, onde 0 é a parte inteira
e 8 é a parte decimal. Aqui observamos que este número decimal é
menor do que 1 porque o numerador é menor do que o
denominador da fração.
Leitura de números decimais
Para ler números decimais é necessário primeiramente, observar a
localização da vírgula que separa a parte inteira da parte decimal.
Um número decimal pode ser colocado na forma genérica:
Centenas Dezenas Unidades , Décimos Centésimos Milésimos
Por exemplo, o número 130,824, pode ser escrito na forma:
1 3 0 8 2 4
,
Centena dezenas unidades décimos centésimos milésimos
Exemplos:
0,6 Seis décimos
0,37 Trinta e sete centésimos
0,189 Cento e oitenta e nove milésimos
3,7 Três inteiros e sete décimos
13,45 Treze inteiros e quarenta e cinco centésimos
130,824 Cento e trinta inteiros e oitocentos e vinte e quatro milésimos

123. Transformando frações decimais em números decimais
Podemos escrever a fração decimal 1/10 como: 0,1. Esta fração é
lida "um décimo". Notamos que a vírgula separa a parte inteira da
parte fracionária:
parte inteira parte fracionária
0 , 1
Uma outra situação nos mostra que a fração decimal 231/100 pode
ser escrita como 2,31, que se lê da seguinte maneira: "dois inteiros
e trinta e um centésimos". Novamente observamos que a vírgula
separa a parte inteira da parte fracionária:
parte inteira parte fracionária
2 , 31
Em geral, transforma-se uma fração decimal em um número decimal
fazendo com que o numerador da fração tenha o mesmo número de
casas decimais que o número de zeros do denominador. Na
verdade, realiza-se a divisão do numerador pelo denominador. Por
exemplo:
(a) 130/100 = 1,30
(b) 987/1000 = 0,987
(c) 5/1000 = 0,005
Transformando números decimais em frações decimais
Também é possível transformar um número decimal em uma fração
decimal. Para isto, toma-se como numerador o número decimal sem
a vírgula e como denominador a unidade (1) seguida de tantos
zeros quantas forem as casas decimais do número dado. Como
exemplo, temos:
(a) 0,5 = 5/10
(b) 0,05 = 5/100

124. (c) 2,41 = 241/100
(d) 7,345 = 7345/1000
Propriedades dos números decimais
Zeros após o último algarismo significativo: Um número decimal não
se altera quando se acrescenta ou se retira um ou mais zeros à
direita do último algarismo não nulo de sua parte decimal. Por
exemplo:
(a) 0,5 = 0,50 = 0,500 = 0,5000
(b) 1,0002 = 1,00020 = 1,000200
(c) 3,1415926535 = 3,141592653500000000
Multiplicação por uma potência de 10: Para multiplicar um número
decimal por 10, por 100, por 1000, basta deslocar a vírgula para a
direita uma, duas, ou três casas decimais. Por exemplo:
(a) 7,4 x 10 = 74
(b) 7,4 x 100 = 740
(c) 7,4 x 1000 = 7400
Divisão por uma potência de 10: Para dividir um número decimal por
10, 100, 1000, etc, basta deslocar a vírgula para a esquerda uma,
duas, três, ... casas decimais. Por exemplo:
(a) 247,5 ÷ 10 = 24,75
(b) 247,5 ÷ 100 = 2,475
(c) 247,5 ÷ 1000 = 0,2475
Operações com números decimais

125. Adição e Subtração: Para efetuar a adição ou a subtração de
números decimais temos que seguir alguns passos:
(a) Igualar a quantidade de casas decimais dos números decimais a
serem somados ou subtraídos acrescentando zeros à direita de
suas partes decimais. Por exemplo:
(a) 2,4 + 1,723 = 2,400 + 1,723
(b) 2,4 - 1,723 = 2,400 - 1,723
(b) Escrever os numerais observando as colunas da parte inteira
(unidades, dezenas, centenas, etc), de forma que:
i. o algarismo das unidades de um número deverá estar
embaixo do algarismo das unidades do outro número,
ii. o algarismo das dezenas de um número deverá estar em
baixo do algarismo das dezenas do outro número,
iii. o algarismo das centenas deverá estar em baixo do algarismo
das centenas do outro número, etc),
iv. a vírgula deverá estar debaixo da outra vírgula, e
v. a parte decimal (décimos, centésimos, milésimos, etc) de
forma que décimos sob décimos, centésimos sob
centésimos, milésimos sob milésimos, etc.
Dois exemplos:
2,400 2,400
+ 1,723 - 1,723
------- -------
(c) Realizar a adição ou a subtração.
Multiplicação de números decimais: Podemos multiplicar dois
números decimais transformando cada um dos números decimais
em frações decimais e realizar a multiplicação de numerador por
numerador e denominador por denominador. Por exemplo:

126. 225 35 225×35 7875
2,25×3,5 = × = = = 7,875
100 10 100×10 1000
Podemos também multiplicar os números decimais como se fossem
inteiros e dar ao produto tantas casas quantas forem as casas do
multiplicando somadas às do multiplicador. Por exemplo:
2,25 2 casas decimais multiplicando
x 3,5 1 casa decimal multiplicador
1125
+ 675
7875
7,875 3 casas decimais Produto
Divisão de números decimais: Como visto anteriormente, se
multiplicarmos tanto o dividendo como o divisor de uma divisão por
10, 100 ou 1000, o quociente não se alterará. Utilizando essas
informações poderemos efetuar divisões entre números decimais
como se fossem divisões de números inteiros. Por exemplo:
3,6÷0,4=?
Aqui, dividendo e divisor têm apenas uma casa decimal, logo
multiplicamos ambos por 10 para que o quociente não se altere.
Assim tanto o dividendo como o divisor serão números inteiros. Na
prática, dizemos que "cortamos" a vírgula.
3,6 36×10 36
3,6÷0,4 = = = =9
0,4 4×10 4
Um outro exemplo:
0,35 0,35×100 35 35÷7 5
0,35÷7= = = = = = 0,05
7 7×100 700 700÷7 100

127. Neste caso, o dividendo tem duas casas decimais e o divisor é um
inteiro, logo multiplicamos ambos por 100 para que o quociente não
se altere. Assim tanto o dividendo como o divisor serão inteiros.
Exercício: Uma pessoa de bom coração doou 35 alqueires paulistas
de terra para 700 pessoas. Sabendo-se que cada alqueire paulista
mede 24.200 metros quadrados, qual será a área que cada um
receberá?
Divisão com o dividendo menor do que o divisor: Vamos considerar
a divisão de 35 (dividendo) por 700 (divisor). Transforma-se o
dividendo, multiplicando-se por 10, 100, ..., para obter 350 décimos,
3500 centésimos, ... até que o novo dividendo fique maior do que o
divisor, para que a divisão se torne possível. Neste caso, há a
necessidade de multiplicar por 100.
Assim a divisão de 35 por 700 será transformada numa divisão de
3500 por 700. Como acrescentamos dois zeros ao dividendo,
iniciamos o quociente com dois zeros, colocando-se uma vírgula
após o primeiro zero. Isto pode ser justificado pelo fato que se
multiplicarmos o dividendo por 100, o quociente ficará dividido por
100.
dividendo 3500 700 divisor
resto 0 0,05 quociente
Realiza-se a divisão de 3500 por 700 para obter 5, concluindo que
0,35/7=35/700=0,05.
Divisão de números naturais com quociente decimal: A divisão de
10 por 16 não fornecerá um inteiro no quociente. Como 10 < 16, o
quociente da divisão não será um inteiro, assim para dividir o
número 10 por 16, montamos uma tabela semelhante à divisão de
dois números inteiros.
10 16
?

128. (1) Multiplicando o dividendo por 10, o quociente ficará dividido por
10. Isto justifica a presença do algarismo 0 seguido de uma vírgula
no quociente.
100 16
0,
(2) Realizamos a divisão de 100 por 16. O resultado será 6 e o resto
será 4.
100 16
-96 0,6
4
(3) O resto 4 corresponde a 4 décimos = 40 centésimos, razão pela
qual colocamos um zero (0) à direita do número 4.
100 16
-96 0,6
40
(4) Dividimos 40 por 16 para obter o quociente 2 e o novo resto será
8.
100 16
-96 0,62
40
-32
8
(5) O resto 8 corresponde a 8 centésimos = 80 milésimos, razão
pela qual inserimos um 0 à direita do número 8. Dividimos 80 por 16
para obter o quociente 5 e o resto igual a 0.
100 16
-96 0,625
40

129. -32
80
-80
0
A divisão 10/16 é igual a 0,625. O o quociente é um número decimal
exato, embora não seja um inteiro.
Comparação de números decimais
A comparação de números decimais pode ser feita analisando-se as
partes inteiras e decimais desses números. Para isso, faremos uso
dos sinais: > (que se lê: maior); < (que se lê: menor) ou = (que se lê:
igual).
Números com partes inteiras diferentes: O maior número é aquele
que tem a parte inteira maior. Por exemplo:
(a) 4,1 > 2,76, pois 4 é maior do que 2.
(b) 3,7 < 5,4, pois 3 é menor do que 5.
Números com partes inteiras iguais: Igualamos o número de casas
decimais acrescentando zeros tantos quantos forem necessários.
Após esta operação, teremos dois números com a mesma parte
inteira mas com partes decimais diferentes. Basta comparar estas
partes decimais para constatar qual é o maior deles. Alguns
exemplos, são:
(a) 12,4 > 12,31 pois 12,4=12,40 e 40 > 31.
(b) 8,032 < 8,47 pois 8,47=8,470 e 032 < 470.
(c) 4,3 = 4,3 pois 4=4 e 3=3.
Porcentagem

130. Ao abrir um jornal, ligar uma televisão, olhar vitrines, é comum
depararmos com expressões do tipo:
A inflação do mês foi de 4% (lê-se quatro por cento)
Desconto de 10% (dez por cento) nas compras à vista.
O índice de reajuste salarial de março é de 0,6% (seis
décimos por cento)
A porcentagem é um modo de comparar números usando a
proporção direta, onde uma das razões da proporção é uma fração
cujo denominador é 100. Toda razão a/b na qual b=100 chama-se
porcentagem.
Exemplos:
(1) Se há 30% de meninas em uma sala de alunos, pode-se
comparar o número de meninas com o número total de alunos da
sala, usando para isto uma fração de denominador 100, para
significar que se a sala tivesse 100 alunos então 30 desses alunos
seriam meninas. Trinta por cento é o mesmo que
30
= 30%
100
(2) Calcular 40% de R$300,00 é o mesmo que determinar um valor
X que represente em R$300,00 a mesma proporção que R$40,00
em R$100,00. Isto pode ser resumido na proporção:
40 X
=
100 300
Como o produto dos meios é igual ao produto dos extremos,
podemos realizar a multiplicação cruzada para obter: 100X=12000,
assim X=120
Logo, 40% de R$300,00 é igual a R$120,00.

131. (3) Li 45% de um livro que tem 200 páginas. Quantas páginas ainda
faltam para ler?
45 X
=
100 200
o que implica que 100X=9000, logo X=90. Como eu já li 90 páginas,
ainda faltam 200-90=110 páginas.
10-Ensino Fundamental: Números Racionais
Números racionais e frações Adição de números racionais
Dízima periódica Produto de números racionais
Números racionais e reais Propriedade distributiva
Geratriz de dízima periódica Potências de números racionais
Números irracionais Raízes de números racionais
Representação, ordem, simetria Médias aritmética e ponderada
Módulo de um número racional Médias geométrica e harmônica
Relacionando números racionais com frações
Um número racional é o que pode ser escrito na forma
m
n
onde m e n são números inteiros, sendo que n deve ser não nulo,
isto é, n deve ser diferente de zero. Frequentemente usamos m/n
para significar a divisão de m por n. Quando não existe
possibilidade de divisão, simplesmente usamos uma letra como q
para entender que este número é um número racional.
Como podemos observar, números racionais podem ser obtidos
através da razão (em Latim: ratio=razão=divisão=quociente) entre
dois números inteiros, razão pela qual, o conjunto de todos os
números racionais é denotado por Q. Assim, é comum
encontrarmos na literatura a notação:

132. Q = {m/n : m e n em Z, n diferente de zero}
Quando há interesse, indicamos Q+ para entender o conjunto dos
números racionais positivos e Q_ o conjunto dos números racionais
negativos. O número zero é também um número racional.
No nosso link Frações já detalhamos o estudo de frações e como
todo número racional pode ser posto na forma de uma fração, então
todas as propriedades válidas para frações são também válidas
para números racionais. Para simplificar a escrita, muitas vezes
usaremos a palavra racionais para nos referirmos aos números
racionais.
Dízima periódica
Uma dízima periódica é um número real da forma:
m,npppp...
onde m, n e p são números inteiros, sendo que o número p se
repete indefinidamente, razão pela qual usamos os três pontos: ...
após o mesmo. A parte que se repete é denominada período.
Em alguns livros é comum o uso de uma barra sobre o período ou
uma barra debaixo do período ou o período dentro de parênteses,
mas, para nossa facilidade de escrita na montagem desta Página,
usaremos o período sublinhado.
Exemplos: Dízimas periódicas
1. 0,3333333... = 0,3
2. 1,6666666... = 1,6
3. 12,121212... = 12,12
4. 0,9999999... = 0,9
5. 7,1333333... = 7,13

133. Uma dízima periódica é simples se a parte decimal é formada
apenas pelo período. Alguns exemplos são:
1. 0,333333... = 0,(3) = 0,3
2. 3,636363... = 3,(63) = 3,63
Uma dízima periódica é composta se possui uma parte que não se
repete entre a parte inteira e o período. Por exemplo:
1. 0,83333333... = 0,83
2. 0,72535353... = 0,7253
Uma dízima periódica é uma soma infinita de números decimais.
Alguns exemplos:
1. 0,3333...= 0,3 + 0,03 + 0,003 + 0,0003 +...
2. 0,8333...= 0,8 + 0,03 + 0,003 + 0,0003 + ...
3. 4,7855...= 4,78 + 0,005 + 0,0005 + ...
A conexão entre números racionais e números reais
Um fato importante que relaciona os números racionais com os
números reais é que todo número real que pode ser escrito como
uma dízima periódica é um número racional. Isto significa que
podemos transformar uma dízima periódica em uma fração.
O processo para realizar esta tarefa será mostrado na sequência
com alguns exemplos numéricos. Para pessoas interessadas num
estudo mais aprofundado sobre a justificativa para o que fazemos
na sequência, deve-se aprofundar o estudo de séries geométricas
no âmbito do Ensino Médio ou mesmo estudar números racionais
do ponto de vista do Cálculo Diferencial e Integral ou da Análise na
Reta no âmbito do Ensino Superior.
A geratriz de uma dízima periódica
Dada uma dízima periódica, qual será a fração que dá origem a esta
dízima? Esta fração é de fato um número racional denominado a

134. geratriz da dízima periódica. Para obter a geratriz de uma dízima
periódica devemos trabalhar com o número dado pensado como
uma soma infinita de números decimais. Para mostrar como
funciona o método, utilizaremos diversos exemplos numéricos.
1. Seja S a dízima periódica 0,3333333..., isto é, S=0,3.
Observe que o período tem apenas 1 algarismo. Iremos
escrever este número como uma soma de infinitos números
decimais da forma:
S = 0,3 + 0,03 + 0,003 + 0,0003 + 0,00003 +...
Multiplicando esta soma "infinita" por 101=10 (o período tem
1 algarismo), obteremos:
10 S = 3 + 0,3 + 0,03 + 0,003 + 0,0003 +...
Observe que são iguais as duas últimas expressões que
aparecem em cor vermelha!
Subtraindo membro a membro a penúltima expressão da
última, obtemos:
10 S - S = 3
donde segue que
9S=3
Simplificando, obtemos:
1
S = = 0,33333... = 0,3
3
Exercício: Usando o mesmo argumento que antes, você
saberia mostrar que:
0,99999... = 0,9 = 1

135. 2. Vamos tomar agora a dízima periódica T=0,313131..., isto é,
T=0,31. Observe que o período tem agora 2 algarismos.
Iremos escrever este número como uma soma de infinitos
números decimais da forma:
T =0,31 + 0,0031 + 0,000031 +...
Multiplicando esta soma "infinita" por 10²=100 (o período tem
2 algarismos), obteremos:
100 T = 31 + 0,31 + 0,0031 + 0,000031 +...
Observe que são iguais as duas últimas expressões que
aparecem em cor vermelha, assim:
100 T = 31 + T
de onde segue que
99 T = 31
e simplificando, temos que
31
T= = 0,31313131... = 0,31
99
3. Um terceiro tipo de dízima periódica é T=7,1888..., isto é,
T=7,18. Observe que existe um número com 1 algarismo
após a vírgula enquanto que o período tem também 1
algarismo. Escreveremos este número como uma soma de
infinitos números decimais da forma:
R = 7,1 + 0,08 + 0,008 + 0,0008 +...

136. Manipule a soma "infinita" como se fosse um número comum
e passe a parte que não se repete para o primeiro membro
para obter:
R-7,1 = 0,08 + 0,008 + 0,0008 +...
Multiplique agora a soma "infinita" por 101=10 (o período tem
1 algarismo), para obter:
10(R-7,1) = 0,8 + 0,08 + 0,008 + 0,0008 +...
Observe que são iguais as duas últimas expressões que
aparecem em cor vermelha!
Subtraia membro a membro a penúltima expressão da última
para obter:
10(R-7,1) - (R-7,1) = 0,8
Assim:
10R - 71 - R + 7,1 = 0,8
Para evitar os números decimais, multiplicamos toda a
expressão por 10 e simplificamos para obter:
90 R = 647
Obtemos então:
647
T= = 7,1888... = 7,18
90
4. Um quarto tipo de dízima periódica é T=7,004004004..., isto
é, U=7,004. Observe que o período tem 3 algarismos, sendo
que os dois primeiros são iguais a zero e apenas o terceiro é

137. não nulo. Decomporemos este número como uma soma de
infinitos números decimais da forma:
U = 7 + 0,004 + 0,004004 + 0,004004004 +...
Manipule a soma "infinita" como se fosse um número comum
e passe a parte que não se repete para o primeiro membro
para obter:
U-7 = 0,004 + 0,004004 + 0,004004004 +...
Multiplique agora a soma "infinita" por 10³=1000 (o período
tem 3 algarismos), para obter:
1000(U-7) = 4 + 0,004 + 0,004004 + 0,004004004 +...
Observe que são iguais as duas últimas expressões que
aparecem em cor vermelha!
Subtraia membro a membro a penúltima expressão da última
para obter:
1000(U-7) - (U-7) = 4
Assim:
1000U - 7000 - U + 7 = 4
Obtemos então
999 U = 6997
que pode ser escrita na forma:
6997
T= = 7,004004... = 7,004
999
Números irracionais

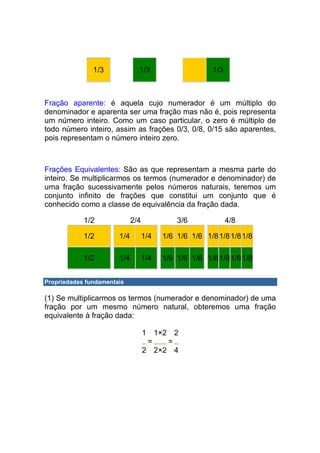
138. Um número real é dito um número irracional se ele não pode ser
escrito na forma de uma fração ou nem mesmo pode ser escrito na
forma de uma dízima periódica.
Exemplo: O número real abaixo é um número irracional, embora
pareça uma dízima periódica:
x=0,10100100010000100000...
Observe que o número de zeros após o algarismo 1 aumenta a
cada passo. Existem infinitos números reais que não são dízimas
periódicas e dois números irracionais muito importantes, são:
e = 2,718281828459045...,
Pi = 3,141592653589793238462643...
que são utilizados nas mais diversas aplicações práticas como:
cálculos de áreas, volumes, centros de gravidade, previsão
populacional, etc...
Exercício: Determinar a medida da diagonal de um quadrado cujo
lado mede 1 metro. O resultado numérico é um número irracional e
pode ser obtido através da relação de Pitágoras. O resultado é a
raiz quadrada de 2, denotada aqui por R[2] para simplificar as
notações estranhas.
Representação, ordem e simetria dos racionais
Podemos representar geometricamente o conjunto Q dos números
racionais através de uma reta numerada. Consideramos o número 0
como a origem e o número 1 em algum lugar e tomamos a unidade
de medida como a distância entre 0 e 1 e por os números racionais
da seguinte maneira:

139. Ao observar a reta numerada notamos que a ordem que os números
racionais obedecem é crescente da esquerda para a direita, razão
pela qual indicamos com uma seta para a direita. Esta consideração
é adotada por convenção, o que nos permite pensar em outras
possibilidades.
Dizemos que um número racional r é menor do que outro número
racional s se a diferença r-s é positiva. Quando esta diferença r-s é
negativa, dizemos que o número r é maior do que s. Para indicar
que r é menor do que s, escrevemos:
r<s
Do ponto de vista geométrico, um número que está à esquerda é
menor do que um número que está à direita na reta numerada.
Todo número racional q exceto o zero, possui um elemento
denominado simétrico ou oposto -q e ele é caracterizado pelo fato
geométrico que tanto q como -q estão à mesma distância da origem
do conjunto Q que é 0. Como exemplo, temos que:
(a) O oposto de 3/4 é -3/4.
(b) O oposto de 5 é -5.
Do ponto de vista geométrico, o simétrico funciona como a imagem
virtual de algo colocado na frente de um espelho que está localizado
na origem. A distância do ponto real q ao espelho é a mesma que a
distância do ponto virtual -q ao espelho.
Módulo de um número racional
O módulo ou valor absoluto de um número racional q é maior valor
entre o número q e seu elemento oposto -q, que é denotado pelo
uso de duas barras verticais | |, por:
|q| = max{-q,q}

140. Exemplos: |0|=0, |2/7|=2/7 e |-6/7|=6/7.
Do ponto de vista geométrico, o módulo de um número racional q é
a distância comum do ponto q até a origem (zero) que é a mesma
distância do ponto -q à origem, na reta numérica racional.
A soma (adição) de números racionais
Como todo número racional é uma fração ou pode ser escrito na
forma de uma fração, definimos a adição entre os números racionais
a/b e c/d, da mesma forma que a soma de frações, através de:
a c ad+bc
+ =
b d bd
Propriedades da adição de números racionais
Fecho: O conjunto Q é fechado para a operação de adição, isto é, a
soma de dois números racionais ainda é um número racional.
Associativa: Para todos a, b, c em Q:
a+(b+c)=(a+b)+c
Comutativa: Para todos a, b em Q:
a+b=b+a
Elemento neutro: Existe 0 em Q, que adicionado a todo q em Q,
proporciona o próprio q, isto é:
q+0=q
Elemento oposto: Para todo q em Q, existe -q em Q, tal que
q + (-q) = 0

141. Subtração de números racionais: A subtração de dois números
racionais p e q é a própria operação de adição do número p com o
oposto de q, isto é:
p - q = p + (-q)
Na verdade, esta é uma operação desnecessária no conjunto dos
números racionais.
A Multiplicação (produto) de números racionais
Como todo número racional é uma fração ou pode ser escrito na
forma de uma fração, definimos o produto de dois números
racionais a/b e c/d, da mesma forma que o produto de frações,
através de:
a c ac
× =
b d bd
O produto dos números racionais a e b também pode ser indicado
por a × b, axb, a.b ou ainda ab sem nenhum sinal entre as letras.
Para realizar a multiplicação de números racionais, devemos
obedecer à mesma regra de sinais que vale em toda a Matemática:
(+1) × (+1) = (+1)
(+1) × (-1) = (-1)
(-1) × (+1) = (-1)
(-1) × (-1) = (+1)
Podemos assim concluir que o produto de dois números com o
mesmo sinal é positivo, mas o produto de dois números com sinais
diferentes é negativo.

142. Propriedades da multiplicação de números racionais
Fecho: O conjunto Q é fechado para a multiplicação, isto é, o
produto de dois números racionais ainda é um número racional.
Associativa: Para todos a, b, c em Q:
a×(b×c)=(a×b)×c
Comutativa: Para todos a, b em Q:
a×b=b×a
Elemento neutro: Existe 1 em Q, que multiplicado por todo q em Q,
proporciona o próprio q, isto é:
q×1=q
Elemento inverso: Para todo q=a/b em Q, q diferente de zero, existe
q-1=b/a em Q, tal que
q × q-1 = 1
Esta última propriedade pode ser escrita como:
a b
× =1
b a
Divisão de números racionais: A divisão de dois números racionais
p e q é a própria operação de multiplicação do número p pelo
inverso de q, isto é:
p ÷ q = p × q-1
Provavelmente você já deve ter sido questionado: Porque a divisão
de uma fração da forma a/b por outra da forma c/d é realizada como
o produto da primeira pelo inverso da segunda?
A divisão de números racionais esclarece a questão:

143. a c a d ad
÷ = × =
b d b c bc
Na verdade, a divisão é um produto de um número racional pelo
inverso do outro, assim esta operação é também desnecessária no
conjunto dos números racionais.
Propriedade distributiva (mista)
Distributiva: Para todos a, b, c em Q:
a×(b+c)=(a×b)+(a×c)
Potenciação de números racionais
A potência qn do número racional q é um produto de n fatores iguais.
O número q é denominado a base e o número n é o expoente.
qn = q × q × q × q × ... × q, (q aparece n vezes)
Exemplos:
(a) (2/5)³ =(2/5) (2/5)×(2/5) = 8/125
(b) (-1/2)³=(-1/2)×(-1/2)×(-1/2) = -1/8
(c) (-5)² =(-5)×(-5) = 25
(d) (+5)² =(+5)×(+5) = 25
Observação: Se o expoente é n=2, a potência q² pode ser lida
como: q elevado ao quadrado e se o expoente é n=3, a potência q³
pode ser lida como: q elevado ao cubo. Isto é proveniente do fato
que área do quadrado pode ser obtida por A=q² onde q é a medida
do lado do quadrado e o volume do cubo pode ser obtido por V=q³
onde q é a medida da aresta do cubo.

144. Raízes de números racionais
A raiz n-ésima (raiz de ordem n) de um número racional q é a
operação que resulta em um outro número racional r que elevado à
potência n fornece o número q. O número n é o índice da raiz
enquanto que o número q é o radicando (que fica sob o estranho
sinal de radical).
Leia a observação seguinte para entender as razões pelas quais
evito usar o símbolo de radical neste trabalho. Assim:
r = Rn[q] equivale a q = rn
Por deficiência da linguagem HTML, que ainda não implementou
sinais matemáticos, denotarei aqui a raiz n-ésima de q por Rn[q].
Quando n=2, simplesmente indicarei a raiz quadrada (de ordem 2)
de um número racional q por R[q].
A raiz quadrada (raiz de ordem 2) de um número racional q é a
operação que resulta em um outro número racional r não negativo
que elevado ao quadrado seja igual ao número q, isto é, r²=q.
Não tem sentido R[-1] no conjunto dos números racionais.
Exemplos:
(a) R³[125] = 5 pois 5³=125.
(b) R³[-125] = -5 pois (-5)³=-125.
(c) R[144] = 12 pois 12²=144.
(d) R[144] não é igual a -12 embora (-12)²=144.
Observação: Não existe a raiz quadrada de um número racional
negativo no conjunto dos números racionais. A existência de um
número cujo quadrado seja igual a um número negativo só será
estudada mais tarde no contexto dos Números Complexos.

145. Erro comum: Frequentemente lemos em materiais didáticos e até
mesmo ocorre em algumas aulas o aparecimento de:
R[9] = ±3
mas isto está errado. O certo é:
R[9] = +3
Não existe um número racional não negativo que multiplicado por
ele mesmo resulte em um número negativo.
A raiz cúbica (de ordem 3) de um número racional q é a operação
que resulta na obtenção de um um outro número racional que
elevado ao cubo seja igual ao número q. Aqui não restringimos os
nossos cálculos são válidos para números positivos, negativos ou o
próprio zero.
Exemplos:
(a) R³[8] = 2, pois 2³ = 8.
(b) R³[-8] = -2, pois (-2)³ = -8.
(c) R³[27] = 3, pois 3³ = 27.
(d) R³[-27]= -3, pois (-3)³ = -27.
Observação: Obedecendo à regra dos sinais para a multiplicação de
números racionais, concluímos que:
(1) Se o índice n da raiz for par, não existe raiz de número racional
negativo.
(2) Se o índice n da raiz for ímpar, é possível extrair a raiz de
qualquer número racional.
Média aritmética e média ponderada

146. Média aritmética: Seja uma coleção formada por n números
racionais: x1, x2, x3, ..., xn. A média aritmética entre esses n números
é a soma dos mesmos dividida por n, isto é:
x1 + x2 + x3 +...+ xn
A=
n
Exemplo: Se um grupo de 9 pessoas tem as idades:
12, 54, 67, 15, 84, 24, 38, 25, 33
então a idade média do grupo pode ser calculada pela média
aritmética:
12 + 54 + 67 + 15 + 84 + 24 + 38 + 25 + 33 352
A= = = 39,11
9 9
o que significa que a idade média está próxima de 39 anos.
Média aritmética ponderada: Consideremos uma coleção formada
por n números racionais: x1, x2, x3, ..., xn, de forma que cada um
esteja sujeito a um peso, respectivamente, indicado por: p1, p2, p3,
..., pn. A média aritmética ponderada desses n números é a soma
dos produtos de cada um por seu peso, dividida por n, isto é:
x1 p1 + x2 p2 + x3 p3 +...+ xn pn
P=
p1 + p2 + p3 +...+ pn
Exemplo: Um grupo de 64 pessoas, que trabalha (com salário por
dia), em uma empresa é formado por sub-grupos com as seguintes
características:
12 ganham R$ 50,00

147. 10 ganham R$ 60,00
20 ganham R$ 25,00
15 ganham R$ 90,00
7 ganham R$ 120,00
Para calcular a média salarial (por dia) de todo o grupo devemos
usar a média aritmética ponderada:
50×12 + 60×10 + 25×20 + 90×15 + 120×7 3890
P= = =60,78
12 + 10 + 20 + 15 + 7 64
Médias geométrica e harmônica
Média geométrica: Consideremos uma coleção formada por n
números racionais não negativos: x1, x2, x3, ..., xn. A média
geométrica entre esses n números é a raiz n-ésima do produto entre
esses números, isto é:
G = Rn[x1 x2 x3 ... xn]
Exemplo: A a média geométrica entre os números 12, 64, 126 e
345, é dada por:
G = R4[12 ×64×126×345] = 76,013
Aplicação prática: Dentre todos os retângulos com a área igual a 64
cm², qual é o retângulo cujo perímetro é o menor possível, isto é, o
mais econômico? A resposta a este tipo de questão é dada pela
média geométrica entre as medidas do comprimento a e da largura
b, uma vez que a.b=64.
A média geométrica G entre a e b fornece a medida desejada.

148. G = R[a × b] = R[64] = 8
Resposta: É o retângulo cujo comprimento mede 8 cm e é lógico
que a altura também mede 8 cm, logo só pode ser um quadrado! O
perímetro neste caso é p=32 cm. Em qualquer outra situação em
que as medidas dos comprimentos forem diferentes das alturas,
teremos perímetros maiores do que 32 cm.
Interpretação gráfica: A média geométrica entre dois segmentos de
reta pode ser obtida geometricamente de uma forma bastante
simples.
Sejam AB e BC segmentos de reta. Trace um segmento de reta que
contenha a junção dos segmentos AB e BC, de forma que eles
formem segmentos consecutivos sobre a mesma reta.
Dessa junção aparecerá um novo segmento AC. Obtenha o ponto
médio O deste segmento e com um compasso centrado em O e raio
OA, trace uma semi-circunferencia começando em A e terminando
em C. O segmento vertical traçado para cima a partir de B
encontrará o ponto D na semi-circunferência. A medida do
segmento BD corresponde à média geométrica das medidas dos
segmentos AB e BC.
Média harmônica: Seja uma coleção formada por n números
racionais positivos: x1, x2, x3, ..., xn. A média harmônica H entre
esses n números é a divisão de n pela soma dos inversos desses n
números, isto é:

149. Aplicações práticas: Para as pessoas interessados em muitas
aplicações do conceito de harmônia, média harmônica e harmônico
global, visite o nosso link Harmonia.
11-Ensino Fundamental: Frações e Números decimais
(Exercícios)
Sugerimos que você tente resolver as questões primeiramente, pois
as respostas estão na página apenas para incentivá-lo a aprender
mais. Para verificar a resposta, posicione o cursor sobre .
1. Qual é a alternativa que representa a fração 9/2 em
números decimais?
2. a. 3,333
3. b. 4,25
4. c. 5,01
5. d. 4,5
6. Qual é a alternativa que representa a fração
35/1000 em números decimais?
7. a. 0,35
8. b. 3,5
9. c. 0,035
10. d. 35
11. Qual é a alternativa que representa o número
0,65 na forma de fração?
12. a. 65/10
13. b. 65/100

150. 14. c. 65/1000
15. d. 65/10000
16. Observe as frações e suas respectivas representações
decimais.
I. 3/1000 = 0,003
II. 2367/100 = 23,67
III. 129/10000 = 0,0129
IV. 267/10 = 2,67
Utilizando as igualdades acima, escolha a
alternativa correta?
a. I e II
b. I e IV
c. I, II e III
d. I, II, III e IV
17. Qual é a alternativa que representa a soma dos
números decimais 0,65 e 0,15?
18. a. 0,70
19. b. 0,77
20. c. 0,67
21. d. 1,00
22. Qual é a alternativa que representa a soma
4,013+10,182?
23. a. 14,313
24. b. 13,920
25. c. 14,213

151. 26. d. 14,083
27. Qual é a alternativa que é igual à subtração do
número decimal 242,12 do número decimal 724,96?
28. a. 48,284
29. b. 586,28
30. c. 241,59
31. d. 482,84
32. Qual é a alternativa que representa a subtração
3,02-0,65?
33. a. 2,37
34. b. 3,37
35. c. 1,32
36. d. 23,7
37. Para cada caso, somar o número de uma linha com o
número de uma coluna. O resultado fica no cruzamento da
linha com a coluna. Clicar sobre o botão para ver se você
acertou a soma?
Soma1,252,5 3,7 6,2
0,25
0,3
38. Para cada caso, subtrair o elemento de cada linha (cor
verde) dos elementos das colunas (cor azul). Pressione os
botões para ver se acertou.
Subtração1,25 2,5 3,7 6,2 Respostas
0,25
0,3
0,07

152. 39. O número decimal 0,03 pode ser escrito por
extenso como:
40. a. três décimos
41. b. três centésimos
42. c. três milésimos
43. Associar o número 15,435 à alternativa que o
representa:
44. a. Quinze inteiros e quatrocentos e
trinta e cinco centésimos
45. b. Cento e cinquenta e quatro e trinta e
cinco centésimos
46. c. Quinze inteiros e quatrocentos e
trinta e cinco milésimos
47. Assinalar a alternativa com a resposta da adição
4/7+2/7:
48. a. 5/7
49. b. 6/14
50. c. 7/6
51. d. 6/7
52. Cada área colorida em cada círculo representa uma
fração de um inteiro.
Qual alternativa representa a soma destas frações?
a. 5/8

153. b. 7/8
c. 9/8
d. 8/7
53. Qual é a fração que representa a parte colorida na
figura?
a. 3/2
b. 6/1
c. 5/6
d. 6/5
54. Associar as frações 3/2, 9/2 e 1/2 com as letras,
segundo os seus devidos lugares na reta numerada.
a. A = 1/2, B = 9/2, C = 3/2
b. A = 9/2, B = 3/2, C = 1/2
c. A = 3/2, B = 1/2, C = 9/2
55. Qual das faixas em azul, na tabela representa a
fração 5/10?
a.
b.
c.
56.

154. 57. Qual é a fração mais simples que equivale a
14/21?
58. Qual das alternativas representa a subtração
8/9-6/9?
59. a. -2/9
60. b. 2/9
61. c. 14/9
62. d. 1/4
63. Cada área colorida em cada círculo representa uma
fração de um inteiro.
Qual é a alternativa que representa a diferença
destas frações indicada na figura?
a. 1/2
b. 3/4
c. 1/4
d. 4/4
64. Usando uma folha de papel ou um caderno, realizar as
operações indicadas abaixo e confirmar as respostas
indicadas.
65. a. 3,9 × 8,2 = 31,98
66. b. 2,315 × 6 = 13,89

155. 67. c. 26,45 : 5 = 5,29
68. d. 58,24 : 2 = 29,12
69. e. 4/5 × 3 × 7 = 12/35
70. f. 6/7 × 5/3 = 10/7
71. g. 2/5 : 8/7 = 7/20
72. h. 7/9 : 3/16 = 112/27
73. Qual alternativa representa a dízima periódica
0,555... ?
74. a. 5/3
75. b. 5/2
76. c. 5/4
77. d. 5/9
78. Quando calculamos 30% de 100, obtemos:
79. a. 10
80. b. 20
81. c. 30
82. d. 40
83. Quando calculamos 3% de 120, obtemos:
84. a. 36
85. b. 3,6
86. c. 0,36
87. d. 360

156. 88. Qual é a alternativa que corresponde a 55% de
$500,00?
89. a. $250,00
90. b. $275,00
91. c. $300,00
92. d. $265,00
93. Qual é a dízima periódica representada pela
fração 10/3?
94. a. 0,333...
95. b. 1,111...
96. c. 3,0303...
97. d. 3,333...
98. Escrever a fração 5/3 na forma de um número
decimal.
99. a. 1,666...
100. b. 1,6060...
101. c. 1,0606...
102. d. 2,1010...
103. Qual é o sinal de desigualdade que deve ser posto em
cada situação abaixo? Para verificar se você acertou a
questão, pressione o botão que aparece em cada caso e
constate que você sabe comparar números decimais?
0,29 0,21 8,9 9,2 1,03 10,2
10,01 9,99 2,09 1,9 0,901 9,01

157. 104. Qual é a palavra: "maior" ou "menor" que ser posta entre
cada par de frações, nas situações abaixo? Pressione o
botão para cada caso e constate que você sabe comparar
frações.
1/5 1/3 2/7 3/9 3/4 1/2
105. Após observar as desigualdades, indique qual é
a alternativa correta.
I. 10,001<9,99
II. 2,09>1,9
III. 9,01<0,901
106. a. I e II estão certas
107. b. II está errada
108. c. I e III estão erradas
109. d. Todas estão erradas
12-Ensino Fundamental: Equações do primeiro grau
Equações 1o.grau: Introdução Sistemas de equações: 1o.grau
Equações 1o.grau: 1 variável O Método de substituição
Desigualdades 1o.grau: 1 var. Relação entre retas e sistemas
Desigualdades 1o.grau: 2 var. Desigualdades com 2 equações
Introdução às equações de primeiro grau
Para resolver um problema matemático, quase sempre devemos
transformar uma sentença apresentada com palavras em uma
sentença que esteja escrita em linguagem matemática. Esta é a
parte mais importante e talvez seja a mais difícil da Matemática.
Sentença com palavras Sentença matemática
2 melancias + 2Kg = 14Kg 2 x + 2 = 14

158. Normalmente aparecem letras conhecidas como variáveis ou
incógnitas. A partir daqui, a Matemática se posiciona perante
diferentes situações e será necessário conhecer o valor de algo
desconhecido, que é o objetivo do estudo de equações.
Equações do primeiro grau em 1 variável
Trabalharemos com uma situação real e dela tiraremos algumas
informações importantes. Observe a balança:
A balança está equilibrada. No prato esquerdo há um "peso" de 2Kg
e duas melancias com "pesos" iguais. No prato direito há um "peso"
de 14Kg. Quanto pesa cada melancia?
2 melancias + 2Kg = 14Kg
Usaremos uma letra qualquer, por exemplo x, para simbolizar o
peso de cada melancia. Assim, a equação poderá ser escrita, do
ponto de vista matemático, como:
2x + 2 = 14
Este é um exemplo simples de uma equação contendo uma
variável, mas que é extremamente útil e aparece na maioria das
situações reais. Valorize este exemplo simples.
Podemos ver que toda equação tem:
Uma ou mais letras indicando valores desconhecidos, que são
denominadas variáveis ou incognitas;
Um sinal de igualdade, denotado por =.

159. Uma expressão à esquerda da igualdade, denominada
primeiro membro ou membro da esquerda;
Uma expressão à direita da igualdade, denominada segundo
membro ou membro da direita.
No link Expressões Algébricas, estudamos várias situações
contendo variáveis. A letra x é a incógnita da equação. A palavra
incógnita significa desconhecida e equação tem o prefixo equa que
provém do Latim e significa igual.
2x+2 = 14
1o. membro sinal de igualdade 2o. membro
As expressões do primeiro e segundo membro da equação são os
termos da equação.
Para resolver essa equação, utilizamos o seguinte processo para
obter o valor de x.
2x + 2 = 14 Equação original
2x + 2 - 2 = 14 - 2 Subtraímos 2 dos dois membros
2x = 12 Dividimos por 2 os dois membros
x=6 Solução
Observação: Quando adicionamos (ou subtraímos) valores iguais
em ambos os membros da equação, ela permanece em equilíbrio.
Da mesma forma, se multiplicamos ou dividimos ambos os
membros da equação por um valor não nulo, a equação permanece
em equilíbrio. Este processo nos permite resolver uma equação, ou
seja, permite obter as raízes da equação.
Exemplos:
1. A soma das idades de André e Carlos é 22 anos. Descubra
as idades de cada um deles, sabendo-se que André é 4
anos mais novo do que Carlos.

160. Solução: Primeiro passamos o problema para a linguagem
matemática. Vamos tomar a letra c para a idade de Carlos e
a letra a para a idade de André, logo a=c-4. Assim:
c + a = 22
c + (c - 4) = 22
2c - 4 = 22
2c - 4 + 4 = 22 + 4
2c = 26
c = 13
Resposta: Carlos tem 13 anos e André tem 13-4=9 anos.
2. A população de uma cidade A é o triplo da população da
cidade B. Se as duas cidades juntas têm uma população de
100.000 habitantes, quantos habitantes tem a cidade B?
Solução: Identificaremos a população da cidade A com a
letra a e a população da cidade com a letra b. Assumiremos
que a=3b. Dessa forma, poderemos escrever:
a + b = 100.000
3b + b = 100.000
4b = 100.000
b = 25.000
Resposta: Como a=3b, então a população de A corresponde
a: a=3×25.000=75.000 habitantes.
3. Uma casa com 260m2 de área construída possui 3 quartos
de mesmo tamanho. Qual é a área de cada quarto, se as
outras dependências da casa ocupam 140m2?

161. Solução: Tomaremos a área de cada dormitório com letra x.
3x + 140 = 260
3x = 260 -140
3x = 120
x = 40
Resposta: Cada quarto tem 40m2.
Exercícios: Resolver as equações
1. 2x + 4 = 10
2. 5k - 12 = 20
3. 2y + 15 - y = 22
4. 9h - 2 = 16 + 2h
Desigualdades do primeiro grau em 1 variável
Relacionadas com as equações de primeiro grau, existem as
desigualdades de primeiro grau, (também denominadas
inequações) que são expressões matemáticas em que os termos
estão ligados por um dos quatro sinais:
< menor
> maior
< menor ou igual
> maior ou igual
Nas desigualdades, o objetivo é obter um conjunto de todas os
possíveis valores que pode(m) assumir uma ou mais incógnitas na
equação proposta.

162. Exemplo: Determinar todos os números inteiros positivos para os
quais vale a desigualdade:
2x + 2 < 14
Para resolver esta desigualdade, seguiremos os seguintes passos:
Passo 1 2x + 2 < 14 Escrever a equação original
Passo 2 2x + 2 - 2 < 14 - 2 Subtrair o número 2 dos dois membros
Passo 3 2x < 12 Dividir pelo número 2 ambos os membros
Passo 4 x<6 Solução
Concluímos que o conjunto solução é formado por todos os
números inteiros positivos menores do que 6:
S = {1, 2, 3, 4, 5}
Exemplo: Para obter todos os números pares positivos que
satisfazem à desigualdade
2x + 2 < 14
obteremos o conjunto solução:
S = {2, 4}
Observação: Se há mais do que um sinal de desigualdade na
expressão, temos várias desigualdades "disfarçadas" em uma.
Exemplo: Para determinar todos os números inteiros positivos para
os quais valem as (duas) desigualdades:
12 < 2x + 2 < 20
poderemos seguir o seguinte processo:
12 < 2x + 2 < 20 Equação original

163. 12 - 2 < 2x + 2 - 2 < 20 - 2 Subtraímos 2 de todos os membros
10 < 2x < 18 Dividimos por 2 todos os membros
5 < x < 9 Solução
O conjunto solução é:
S = {6, 7, 8, 9}
Exemplo: Para obter todos os números inteiros negativos que
satisfazem às (duas) desigualdades
12 < 2x + 2 < 20
obteremos apenas o conjunto vazio, como solução, isto é:
S=Ø={}
Desigualdades do primeiro grau em 2 variáveis
Uma situação comum em aplicações é aquela em que temos uma
desigualdade envolvendo uma equação com 2 ou mais incógnitas.
Estudaremos aqui apenas o caso em aparecem 2 incógnitas x e y.
Uma forma geral típica, pode ser:
ax+by<c
onde a, b e c são valores dados.
Exemplo: Para obter todos os pares ordenados de números reais
para os quais:
2x + 3y > 0
observamos que o conjunto solução contém os pares:
(0,0), (1,0), (0,1), (-1,1), (1,-1), ...

164. Há infinitos pares ordenados de números reais satisfazendo a esta
desigualdade, o que torna impossível exibir todas as soluções. Para
remediar isto, utilizaremos um processo geométrico que permitirá
obter uma solução geométrica satisfatória.
Processo geométrico:
(1) Traçamos a reta 2x+3y=0;
(2) Escolhemos um par ordenado, como (1,1), fora da reta;
(3) Se (1,1) satisfaz à desigualdade 2x+3y>0, colorimos a região
que contém este ponto, caso contrário, colorimos a região que está
do outro lado da reta.
(4) A região colorida é o conjunto solução para a desigualdade.
Sistemas linear de equações do primeiro grau
Uma equação do primeiro grau, é aquela em que todas as
incógnitas estão elevadas à potência 1. Este tipo de equação
poderá ter mais do que uma incógnita.
Um sistema de equações do primeiro grau em duas incógnitas x e y,
é um conjunto formado por duas equações do primeiro nessas duas
incógnitas.
Exemplo: Seja o sistema de duas equações:
2 x + 3 y = 38
3 x - 2 y = 18

165. Resolver este sistema de equações é o mesmo que obter os valores
de x e de y que satisfazem simultaneamente a ambas as equações.
x=10 e y=6 são as soluções deste sistema e denotamos esta
resposta como um par ordenado de números reais:
S = { (10,6) }
Método de substituição para resolver este sistema
Entre muitos outros, o método da substituição, consiste na idéia
básica de isolar o valor algébrico de uma das variáveis, por exemplo
x, e, aplicar o resultado à outra equação.
Para entender o método, consideremos o sistema:
2 x + 3 y = 38
3 x - 2 y = 18
Para extrair o valor de x na primeira equação, usaremos o seguinte
processo:
2x + 3y = 38 Primeira equação
2x + 3y - 3y = 38 - 3y Subtraímos 3y de ambos os membros
2x = 38 - 3y Dividimos ambos os membros por 2
x = 19 - (3y/2) Este é o valor de x em função de y
Substituímos aqora o valor de x na segunda equação 3x-2y=18:
3x - 2y = 18 Segunda equação
3(19 - (3y/2)) - 2y = 18 Após substituir x, eliminamos os parênteses
57 - 9y/2 - 2y = 18 multiplicamos os termos por 2
114 - 9y - 4y = 36 reduzimos os termos semelhantes
114 - 13y = 36 separamos variáveis e números
114 - 36 = 13y simplificamos a equação

166. 78 = 13y mudamos a posição dos dois membros
13 y = 78 dividimos ambos os membros por 6
y=6 Valor obtido para y
Substituindo y=6 na equação x=19-(3y/2), obtemos:
x = 19 - (3×6/2) = 19 - 18/2 = 19-9 = 10
Exercício: Determinar a solução do sistema:
x+y=2
x-y=0
Cada equação do sistema acima pode ser visto como reta no plano
cartesiano. Construa as duas retas no plano e verifique que, neste
caso, a solução é um par ordenado que pertence à interseção das
duas retas.
Relação entre sistemas lineares e retas no plano
No contexto que estamos trabalhando aqui, cada equação da forma
ax+by=c, representa uma reta no plano cartesiano. Um sistema com
duas equações de primeiro grau em 2 incógnitas sempre pode ser
interpretado como um conjunto de duas retas localizadas no plano
cartesiano.
Reta 1: ax + by = c
Reta 2: dx + ey = f
Há três modos de construir retas no plano: retas concorrentes, retas
paralelas e retas coincidentes.
Se o sistema é formado por duas equações que são retas no plano
cartesiano, temos a ocorrência de:

167. Retas concorrentes: quando o sistema admite uma única solução
que é um par ordenado localizado na interseção das duas retas;
Retas paralelas: quando o não admite solução, pois um ponto não
pode estar localizado em duas retas paralelas;
Retas coincidentes: quando o admite uma infinidade de soluções
pois as retas estão sobrepostas.
Exemplos das três situações
Tipos de retas Sistema
x+y=2
Concorrentes
x-y=0
x+y=2
Paralelas
x+y=4
x+y=2
Coincidentes
2x + 2y = 4
Problemas com sistemas de equações:
1. A soma das idades de André e Carlos é 22 anos. Descubra
as idades de cada um deles, sabendo-se que André é 4
anos mais novo do que Carlos.
Solução: A idade de André será tomada com a letra A e a
idade de Carlos com a letra C. O sistema de equações será:
C + A = 22
C - A = 4
Resposta: C = 13 e A = 9
2. A população de uma cidade A é o triplo da população da
cidade B. Se as duas cidades juntas têm uma população de
100.000 habitantes, quantos habitantes tem a cidade B?

168. Solucão: Identificando a população da cidade A com a letra
A e a população da cidade B com B, o sistema de equações
será:
A + B = 100000
A = 3B
Resposta: A = 75000, B= 25000.
3. Uma casa com 260m2 de área construída tem 3 dormitórios
de mesmo tamanho. Qual é a área de cada dormitório se as
outras dependências da casa ocupam 140m2?
Solução: Identificaremos a área de cada dormitório com a
letra D e a área das outras dependências com a letra O.
Assim, o sistema será:
3D + O = 260
O = 140
Resposta: D = 40
Desigualdades com 2 Equações em 2 variáveis
Outra situação bastante comum é aquela em que existe uma
desigualdade com 2 equações em 2 ou mais incógnitas.
Estudaremos aqui apenas o caso em aparecem 2 equações e 2
incógnitas x e y. Uma forma geral pode ter a seguinte forma típica:
ax+by<c
dx+ey>f
onde as constantes: a, b, c, d, e, f; são conhecidas.
Exemplo: Determinar todos os pares ordenados de números reais
para os quais:

169. 2x + 3y > 6
5x + 2y < 20
Há infinitos pares ordenados de números reais satisfazendo a esta
desigualdade, o que torna impossível exibir todas as soluções. Para
remediar isto, utilizaremos um processo geométrico que permitirá
obter uma solução geométrica satisfatória.
Processo geométrico:
(1) Traçar a reta 2x+3y=6 (em vermelho);
(2) Escolher um ponto fora da reta, como o par (2,2) e observar que
ele satisfaz à primeira desigualdade;
(3) Devemos colorir o semi-plano contendo o ponto (2,2) (em verde);
(4) Traçar a reta 5x+2y=20 (em azul);
(5) Escolher um ponto fora da reta, por exemplo, o próprio par já
usado antes (2,2) (não é necessário que seja o mesmo) e
observamos que ele satisfaz à segunda desigualdade;
(6) Colorir o semi-plano contendo o ponto (2,2), inclusive a própria
reta. (cor azul)
(7) Construir a interseção (em vermelho) das duas regiões coloridas.
(8) Esta interseção é o conjunto solução para o sistema com as
duas desigualdades.

170. Esta situação gráfica é bastante utilizada em aplicações da
Matemática a estudos de Economia e Processos de otimização. Um
dos ramos da Matemática que estuda este assunto é a Pesquisa
Operacional.
13-Ensino Fundamental: Razões e Proporções
Razões
Polígonos Semelhantes
Proporções
Figuras Semelhantes
Propriedade fundamental
Aplicações práticas das razões
Razões/Proporções de segmentos
Razões
A palavra razão vem do latim ratio e significa a divisão ou o
quociente entre dois números A e B, denotada por:
A
B
Exemplo: A razão entre 12 e 3 é 4 porque:
12
=4
3
e a razão entre 3 e 6 é 0,5 pois:
3
= 0,5
6
A razão também pode ser expressa na forma de divisão entre duas
grandezas de algum sistema de medidas. Por exemplo, para
preparar uma bebida na forma de suco, normalmente adicionamos
A litros de suco concentrado com B litros de água. A relação entre a
quantidade de litros de suco concentrado e de água é um número
real expresso como uma fração ou razão (que não tem unidade), é a
razão:

171. A
= A/B
B
Exemplo: Tomemos a situação apresentada na tabela abaixo.
Líquido Situação1 Situação2 Situação3 Situação4
Suco puro 3 6 8 30
Água 8 16 32 80
Suco pronto 11 22 40 110
Na Situação1, para cada 3 litros de suco puro coloca-se 8 litros de
água, perfazendo o total de 11 litros de suco pronto.
Na Situação2, para cada 6 litros de suco puro coloca-se 16 litros de
água, perfazendo o total de 24 litros de suco pronto.
Exemplo: Em uma partida de basquete um jogador faz 20
arremessos e acerta 10.
Podemos avaliar o aproveitamento desse jogador, dividindo o
número de arremessos que ele acertou pelo total de arremessos, o
que significa que o jogador acertou 1 para cada dois arremessos, o
que também pode ser pensado como o acerto de 0,5 para cada
arremesso.
10 : 20 = 1 : 2 = 0,5
Proporções

172. Proporção é a igualdade entre duas razões. A proporção entre A/B e
C/D é a igualdade:
A C
=
B D
Notas históricas: A palavra proporção vem do latim proportione e
significa uma relação entre as partes de uma grandeza, ou seja, é
uma igualdade entre duas razões. No século XV, o matemático
árabe Al-Kassadi empregou o símbolo "..." para indicar as
proporções e em 1.537, o italiano Niccola Fontana, conhecido por
Tartaglia, escreveu uma proporção na forma
6:3::8:4.
Regiomontanus foi um dos matemáticos italianos que mais divulgou
o emprego das proporções durante o período do Renascimento.
Propriedade fundamental das proporções
Numa proporção:
A C
=
B D
os números A e D são denominados extremos enquanto os
números B e C são os meios e vale a propriedade: o produto dos
meios é igual ao produto dos extremos, isto é:
A·D=B·C
Exemplo: A fração 3/4 está em proporção com 6/8, pois:
3 6
=
4 8

173. Exercício: Determinar o valor de X para que a razão X/3 esteja em
proporção com 4/6.
Solução: Deve-se montar a proporção da seguinte forma:
x 4
=
3 6
Para obter X=2.
Razões e Proporções de Segmentos
Consideremos dois segmentos AB e CD, cujas medidas são dadas,
respectivamente, por 2cm e 4cm.
A________B, C ______________ D
Comparando os segmentos AB e CD, estabelecemos uma razão
entre as suas medidas.
m(AB) 2
=
m(CD) 4
Podemos também afirmar que AB está para CD na razão de 1 para
2 ou que CD está para AB na razão de 2 para 1.
Polígonos Semelhantes
Dois polígonos são semelhantes se têm ângulos correspondentes
congruentes e os lados correspondentes proporcionais.
Exemplo: Sejam os triângulos ABC e RST.

174. Observamos que os ângulos correspondentes possuem as mesmas
medidas, denotadas aqui por, A~R, B~S, C~T e os lados
correspondentes são proporcionais.
AB/RS=5/(2,5)=2 BC/ST=4/2=2 AC/RT=3/(1,5)=2
Afirmamos que os polígonos (triângulos) ABC e RST são
semelhantes e indicamos isto por :
ABC ~ DEF
Figuras Semelhantes
Duas figuras são semelhantes quando elas têm a mesma forma
com medidas correspondentes congruentes, ou seja, quando uma é
uma ampliação ou redução da outra. Isto significa que existe uma
proporção constante entre elas sem ocorrência de deformação. A
figura final e a figura original são chamadas figuras semelhantes.
As figuras geométricas são semelhantes quando existe uma
igualdade entre as razões dos segmentos que ocupam as
correspondentes posições relativas nas figuras.
Exemplo: Nos triângulos

175. observamos que os ângulos correspondentes possuem a mesma
medida, ou seja, A=R, B=S e C=T e os lados correspondentes são
proporcionais.
AB/RS = BC/ST = CA/TR = 2
Assim, os triângulos ABC e DEF são semelhantes e indicamos por:
ABC ~ DEF
Exemplo: O mapa do Brasil está em duas escalas diferentes.
Os dois mapas possuem a mesma forma mas têm tamanhos
diferentes. O mapa verde é uma ampliação do mapa amarelo ou o
mapa amarelo é uma redução do mapa verde.
Aplicações práticas das razões
Existem algumas razões especiais muito utilizadas em nosso
cotidiano, entre as quais: velocidade média, escala, densidade
demográfica e densidade de um corpo.
1. Velocidade Média: A "velocidade média", em geral, é uma
grandeza obtida pela razão entre uma distância percorrida
(expressa em quilômetros ou metros) e um tempo por ele
gasto (expresso em horas, minutos ou segundos).
vmédia = distância percorrida / tempo gasto

176. Exemplo: Suponhamos que um carro de Fórmula MAT
percorreu 328Km em 2h. Qual foi a velocidade média do
veículo nesse percurso?
A partir dos dados do problema, teremos:
vmédia = 328 Km / 2h = 164 Km/h
o que significa que a velocidade média do veículo durante a
corrida foi de 164 Km/h, ou seja, para cada hora percorrida o
carro se deslocou 164 Km.
2. Escala: Uma das aplicações da razão entre duas grandezas
se encontra na escala de redução ou escala de ampliação,
conhecidas simplesmente como escala. Chamamos de
escala de um desenho à razão entre o comprimento
considerado no desenho e o comprimento real
correspondente, ambos medidos na mesma unidade.
escala = comprimento no desenho / comprimento real
Usamos escala quando queremos representar um esboço
gráfico de objetos como móveis, plantas de uma casa ou de
uma cidade, fachadas de prédios, mapas, maquetes, etc.
Exemplo: Observemos as figuras dos barcos:

177. Base menor barco azul/Base menor barco vermelho = 2/4
Base maior barco azul/Base maior barco vermelho = 4/8
Altura do barco azul/Altura do barco vermelho = 3/6
O barco vermelho é uma ampliação do barco azul, pois as
dimensões do barco vermelho são 2 vezes maiores do que
as dimensões do barco azul, ou seja, os lados
correspondentes foram reduzidos à metade na mesma
proporção.
3. Densidade Demográfica: O cálculo da densidade
demográfica, também chamada de população relativa de
uma região é considerada uma aplicação de razão entre
duas grandezas. Ela expressa a razão entre o numero de
habitantes e a área ocupada em uma certa região.
Exemplo: Em um jogo de vôlei há 6 jogadores para cada
time, o que significa 6 jogadores em cada lado da quadra.
Se, por algum motivo, ocorre a expulsão de 1 jogador de um
time, sendo que não pode haver substituição, observa-se
que sobra mais espaço vazio para ser ocupado pelo time
que tem um jogador expulso. Neste caso, afirmamos que a
densidade demográfica é menor na quadra que tem um
jogador expulso e maior na outra quadra.

178. Exemplo: Um estado brasileiro ocupa a área de 200.000
Km². De acordo com o censo realizado, o estado tem uma
população aproximada de 12.000.000 habitantes. Assim:
dens.demográfica=12.000.000 habitantes/200.000 Km²
densidade demográfica = 60 habitantes/ Km2
Isto significa que para cada 1 Km2existem aproximadamente
60 habitantes.
4. Densidade de um Corpo: Densidade de um corpo é mais
uma aplicação de razão entre duas grandezas. Assim, a
densidade (volumétrica) de um corpo é a razão entre a
massa desse corpo, medida em Kg ou gramas e o seu
volume, medido em m³, dm³ ou qualquer outra unidade de
volume.
Exemplo: Se uma estátua de bronze possui uma densidade
volumétrica de 8,75 kg/dm³ então para cada dm³ há uma
massa de 8,75 kg.
Curiosidade:Devido à existência de densidades diferentes,
observamos que ao colocarmos corpos diferentes em um
recipiente com água, alguns afundam e outros flutuam.
Uma bolinha de isopor flutuará na água enquanto que uma
de chumbo, de mesmo volume afundará. Isso ocorre porque
a densidade do chumbo é maior que a densidade do isopor.
Algumas substâncias e suas densidades estão na tabela
abaixo:
Substância Densidade [g/cm³]
madeira 0,5

179. gasolina 0,7
álcool 0,8
alumínio 2,7
ferro 7,8
mercúrio 13,6
5. Pi: Uma razão muito famosa: Os egípcios trabalhavam muito
com certas razões e descobriram a razão entre o
comprimento de uma circunferência e seu diâmetro. Este é
um fato fundamental pois esta razão é a mesma para toda
circunferência. O nome desta razão é Pi e seu valor é
aproximadamente:
Pi = 3,1415926535
Exemplo: Se C é o comprimento da circunferência e D a
medida do diâmetro da circunferência, temos uma razão
notável:
C / D = Pi = 3,14159265358979323846264338327950...
significando que
C = Pi . D
Exemplo: Se a medida do raio de uma circunferência tem
1,5cm então o perímetro da circunferência é igual a 9,43cm.
14-Ensino Fundamental: Aplicações das Razões e Proporções
Proporções com números Regras de três simples direta
Propriedades das Proporções Regras de três simples inversa
Grandezas diret. proporcionais Regras de três composta
Grandezas invers. proporcionais Porcentagem
Histórico sobre a Regra de três Juros simples
Proporções com números

180. Quatro números racionais A, B, C e D diferentes de zero, nessa
ordem, formam uma proporção quando:
A C
=
B D
1. Os números A, B, C e D são denominados termos
2. Os números A e B são os dois primeiros termos
3. Os números C e D são os dois últimos termos
4. Os números A e C são os antecedentes
5. Os números B e D são os consequentes
6. A e D são os extremos
7. B e C são os meios
8. A divisão entre A e B e a divisão entre C e D, é uma
constante K, denominada constante de proporcionalidade K
dessa razão.
Propriedades das proporções
Para a proporção
A C
=
B D
valem as seguintes propriedades:
1. O produto dos meios é igual ao produto dos extremos, isto é:
A·D=B·C
2. A soma (diferença) dos dois primeiros termos está para o
primeiro termo, assim como a soma (diferença) dos dois
últimos está para o terceiro termo, isto é:
A+B = C+D e A-B = C-D

181. A C A C
3. A soma (diferença) dos dois primeiros termos está para o
segundo termo, assim como a soma (diferença) dos dois
últimos está para o quarto termo, isto é:
A+B C+D A-B C-D
= e =
B D B D
4. A soma (diferença) dos antecedentes está para a soma
(diferença) dos consequentes, assim como cada
antecedente está para o seu consequente, isto é:
A+C A A-C A+C A-C C
= = e = =
B+D B B-D B+D B-D D
Grandezas Diretamente Proporcionais
Duas grandezas são diretamente proporcionais quando,
aumentando uma delas, a outra também aumenta na mesma
proporção, ou, diminuindo uma delas, a outra também diminui na
mesma proporção.
Se duas grandezas X e Y são diretamente proporcionais, os
números que expressam essas grandezas variam na mesma razão,
isto é, existe uma constante K tal que:
X
=K
Y
Exemplos:
1. Uma torneira foi aberta para encher uma caixa com água
azul. A cada 15 minutos é medida a altura do nível de água.
(cm=centímetros e min=minutos)

182. 15 minutos 30 minutos 45 minutos
50 cm 100 cm 150 cm
2. Construímos uma tabela para mostrar a evolução da
ocorrência:
Tempo (min) Altura (cm)
15 50
30 100
45 150
3. Observamos que quando duplica o intervalo de tempo, a
altura do nível da água também duplica e quando o intervalo
de tempo é triplicado, a altura do nível da água também é
triplicada.
4. Observações: Usando razões, podemos descrever essa
situação de outro modo.
5. (a) Quando o intervalo de tempo passa de 15 min para 30
min, dizemos que o tempo varia na razão 15/30, enquanto
que a altura da água varia de 50 cm para 100 cm, ou seja, a
altura varia na razão 50/100. Observamos que estas duas
razões são iguais:
15 50 1
= =
30 100 2
6. (b) Quando o intervalo de tempo varia de 15 min para 45
min, a altura varia de 50 cm para 150 cm. Nesse caso, o
tempo varia na razão 15/45 e a altura na razão 50/150.
Então, notamos que essas razões são iguais:

183. 15 50 1
= =
45 150 3
7. Concluímos que a razão entre o valor numérico do tempo
que a torneira fica aberta e o valor numérico da altura
atingida pela água é sempre igual, assim dizemos então que
a altura do nível da água é diretamente proporcional ao
tempo que a torneira ficou aberta.
8. Em média, um automóvel percorre 80 Km em 1 hora, 160
Km em 2 horas e 240 Km em 3 horas. (Km=quilômetro,
h=hora). Construímos uma tabela da situação:
Distância (Km) Tempo (h)
80 1
160 2
240 3
9. Notamos que quando duplica o intervalo de tempo, duplica
também a distância percorrida e quando o intervalo de
tempo é triplicado, a distância também é triplicada, ou seja,
quando o intervalo de tempo aumenta, a distância percorrida
também aumenta na mesma proporção.
10. Observações: Usando razões e proporções, podemos
descrever essa situação de outro modo.
11. (a) Quando o intervalo de tempo aumenta de 1 h para 2
h, a distância percorrida varia de 80 Km para 160 Km, ou
seja, o tempo varia na razão de 1/2 enquanto a distância
percorrida varia na razão 80/160. Assim temos que tais
razões são iguais, isto é:
1 80 1
= =
2 160 3
12. (b) Quando o intervalo de tempo varia de 2 h para 3 h, a
distância percorrida varia de 160 Km para 240 Km. Nesse
caso, o tempo varia na razão 2/3 e a distância percorrida na

184. razão 160/240 e observamos que essas razões são iguais,
isto é:
2 160 1
= =
3 240 3
13. Concluímos que o tempo gasto e a distância percorrida,
variam sempre na mesma razão e isto significa que a
distância percorrida é diretamente proporcional ao tempo
gasto para percorrê-la, se a velocidade média do automóvel
se mantiver constante.
Grandezas Inversamente Proporcionais
Duas grandezas são inversamente proporcionais quando,
aumentando uma delas, a outra diminui na mesma proporção, ou,
diminuindo uma delas, a outra aumenta na mesma proporção. Se
duas grandezas X e Y são inversamente proporcionais, os números
que expressam essas grandezas variam na razão inversa, isto é,
existe uma constante K tal que:
X·Y=K
Exemplos:
1. A professora de um colégio, tem 24 livros para distribuir
entre os seus melhores alunos, dando a mesma quantidade
de livros para cada aluno.
2. o melhor aluno receberá 24 livros
3. cada um dos 2 melhores alunos receberá 12
livros
4. cada um dos 3 melhores alunos receberá 8
livros
5. cada um dos 4 melhores alunos receberá 6
livros

185. 6. cada um dos 6 melhores alunos receberá 4
livros
Alunos escolhidos Livros para cada aluno
1 24
2 12
3 8
4 6
6 4
7. De acordo com a tabela, a quantidade de alunos escolhidos
e a quantidade de livros que cada aluno receberá, são
grandezas que variam sendo que uma depende da outra e
se relacionam da seguinte forma:
1. Se o número de alunos dobra, o número de livros que
cada um vai receber cai para a metade.
2. Se o número de alunos triplica, o número de livros que
cada aluno vai receber cai para a terça parte.
3. Se o número de alunos quadruplica, o número de livros
que cada aluno vai receber cai para a quarta parte.
4. Se o número de alunos sextuplica, o número de livros
que cada aluno vai receber cai para a sexta parte.
Sob estas condições, as duas grandezas envolvidas
(número de alunos escolhidos e número de livros
distribuídos) são grandezas inversamente proporcionais.
Quando a quantidade de alunos varia na razão de 2 para 4,
a quantidade de livros distribuídos varia de 12 para 6.
Notemos que essas razões não são iguais, mas são
inversas:
2 1 1 12 1
= = e = =2
4 12/6 2 6 2/4

186. Se a quantidade de alunos varia na razão de 2 para 6, a
quantidade de livros distribuídos varia de 12 para 4.
Observemos que essas razões não são iguais, mas são
inversas:
2 1 12 1
= e =
6 12/4 4 2/6
Representamos tais grandezas inversamente proporcionais
com a função f(x)=24/x, apresentada no gráfico
8. Um automóvel se desloca de uma cidade até uma outra
localizada a 120 Km da primeira. Se o percurso é realizado
em:
9. 1 hora, velocidade média de 120 Km/h
10. 2 horas, velocidade média de 60 Km/h
11. 3 horas, velocidade média de 40 Km/h
A unidade é Km/h=quilômetro por hora e uma tabela da
situação é:
Velocidade (Km/h) Tempo (h)
120 1
60 2
40 3

187. De acordo com a tabela, o automóvel faz o percurso em 1
hora com velocidade média de 120 Km/h. Quando diminui a
velocidade à metade, ou seja 60 Km/h, o tempo gasto para
realizar o mesmo percurso dobra e quando diminui a
velocidade para a terça parte, 40 Km/h o tempo gasto para
realizar o mesmo percurso triplica.
Para percorrer uma mesma distância fixa, as grandezas
velocidade e tempo gasto, são inversamente proporcionais.
Elementos históricos sobre a Regra de três
Embora os gregos e os romanos conhecessem as proporções, não
chegaram a aplicá-las na resolução de problemas. Na Idade Média,
os árabes revelaram ao mundo a "Regra de Três". No século XIII, o
italiano Leonardo de Pisa difundiu os princípios dessa regra em seu
Liber Abaci (o livro do ábaco), com o nome de Regra dos três
números conhecidos.
Regra de três simples direta
Uma regra de três simples direta é uma forma de relacionar
grandezas diretamente proporcionais.
Para resolver problemas, tomaremos duas grandezas diretamente
proporcionais X e Y e outras duas grandezas W e Z também
diretamente proporcionais, de forma que tenham a mesma
constante de proporcionalidade K.
X W
=K e =K
Y Z
assim
X W
=
Y Z

188. Exemplo: Na extremidade de uma mola (teórica!) colocada
verticalmente, foi pendurado um corpo com a massa de 10Kg e
verificamos que ocorreu um deslocamento no comprimento da mola
de 54cm. Se colocarmos um corpo com 15Kg de massa na
extremidade dessa mola, qual será o deslocamento no comprimento
da mola? (Kg=quilograma e cm=centímetro).
Representaremos pela letra X a medida procurada. De acordo com
os dados do problema, temos:
Massa do corpo (Kg) Deslocamento da mola (cm)
10 54
15 X
As grandezas envolvidas: massa e deslocamento, são diretamente
proporcionais. Conhecidos três dos valores no problema, podemos
obter o quarto valor X, e, pelos dados da tabela, podemos montar a
proporção:
10 54
=
15 X
Observamos que os números 10 e 15 aparecem na mesma ordem
que apareceram na tabela e os números 54 e X também aparecem
na mesma ordem direta que apareceram na tabela anterior e desse
modo 10·X=15·54, logo 10X=810, assim X=81 e o deslocamento da
mola será de 81cm.
Regra de três simples inversa
Uma regra de três simples inversa é uma forma de relacionar
grandezas inversamente proporcionais para obter uma proporção.
Na resolução de problemas, consideremos duas grandezas
inversamente proporcionais A e B e outras duas grandezas também

189. inversamente proporcionais C e D de forma que tenham a mesma
constante de proporcionalidade K.
A·B=K e C·D=K
segue que
A·B=C·D
logo
A D
=
C B
Exemplo: Ao participar de um treino de Fórmula 1, um corredor
imprimindo a velocidade média de 180 Km/h fez um certo percurso
em 20s. Se a sua velocidade média fosse de 200 Km/h, qual seria o
tempo gasto no mesmo percurso? (Km/h=quilômetro por hora,
s=segundo). Representaremos o tempo procurado pela letra T. De
acordo com os dados do problema, temos:
Velocidade (Km/h) Tempo (s)
180 20
200 T
Relacionamos grandezas inversamente proporcionais: velocidade e
tempo em um mesmo espaço percorrido. Conhecidos três valores,
podemos obter um quarto valor T.
180 T
=
200 20
Os números 180 e 200 aparecem na mesma ordem que
apareceram na tabela, enquanto que os números 20 e T aparecem
na ordem inversa da ordem que apareceram na tabela acima.

190. Assim 180.20=200.X, donde segue que 200X=3600 e assim
X=3600/200=18. Se a velocidade do corredor for de 200 Km/h ele
gastará 18s para realizar o mesmo percurso.
Regra de três composta
Regra de três composta é um processo de relacionamento de
grandezas diretamente proporcionais, inversamente proporcionais
ou uma mistura dessas situações.
O método funcional para resolver um problema dessa ordem é
montar uma tabela com duas linhas, sendo que a primeira linha
indica as grandezas relativas à primeira situação enquanto que a
segunda linha indica os valores conhecidos da segunda situação.
Se A1, B1, C1, D1, E1, ... são os valores associados às grandezas
para uma primeira situação e A2, B2, C2, D2, E2, ... são os valores
associados às grandezas para uma segunda situação, montamos a
tabela abaixo lembrando que estamos interessados em obter o valor
numérico para uma das grandezas, digamos Z2 se conhecemos o
correspondente valor numérico Z1 e todas as medidas das outras
grandezas.
Situação Grandeza 1 Grandeza 2 Grandeza 3 Grandeza 4 Grandeza 5 Grand... Grandeza ?
Situação 1 A1 B1 C1 D1 E1 … Z1
Situação 2 A2 B2 C2 D2 E2 … Z2
Quando todas as grandezas são diretamente proporcionais à
grandeza Z, resolvemos a proporção:
Z1 A1 · B1 · C1 · D1 · E1 · F1 …
=
Z2 A2 · B2 · C2 · D2 · E2 · F2 …
Quando todas as grandezas são diretamente proporcionais à
grandeza Z, exceto a segunda grandeza (com a letra B, por

191. exemplo) que é inversamente proporcional à grandeza Z,
resolvemos a proporção com B1 trocada de posição com B2:
Z1 A1 · B2 · C1 · D1 · E1 · F1 …
=
Z2 A2 · B1 · C2 · D2 · E2 · F2 …
As grandezas que forem diretamente proporcionais à grandeza Z
são indicadas na mesma ordem (direta) que aparecem na tabela
enquanto que as grandezas que forem inversamente proporcionais
à grandeza Z aparecerão na ordem inversa daquela que
apareceram na tabela.
Por exemplo, se temos cinco grandezas envolvidas: A, B, C, D e Z,
sendo a primeira A e a terceira C diretamente proporcionais à
grandeza Z e as outras duas B e D inversamente proporcionais à
grandeza Z, deveremos resolver a proporção:
Z1 A1 · B2 · C1 · D2
=
Z2 A2 · B1 · C2 · D1
Observação: O problema difícil é analisar de um ponto de vista
lógico quais grandezas são diretamente proporcionais ou
inversamente proporcionais. Como é muito difícil realizar esta
análise de um ponto de vista geral, apresentaremos alguns
exemplos para entender o funcionamento da situação.
Exemplos:
1. Funcionando durante 6 dias, 5 máquinas produziram 400
peças de uma mercadoria. Quantas peças dessa mesma
mercadoria serão produzidas por 7 máquinas iguais às
primeiras, se essas máquinas funcionarem durante 9 dias?
Vamos representar o número de peças pela letra X. De
acordo com os dados do problema, vamos organizar a
tabela:

192. No. de máquinas (A) No. de dias (B) No. de peças (C)
5 6 400
7 9 X
A grandeza Número de peças (C) servirá de referência para
as outras grandezas. Analisaremos se as grandezas Número
de máquinas (A) e Número de dias (B) são diretamente
proporcionais ou inversamente proporcionais à grandeza C
que representa o Número de peças. Tal análise deve ser
feita de uma forma independente para cada par de
grandezas.
Vamos considerar as grandezas Número de peças e
Número de máquinas. Devemos fazer uso de lógica para
constatar que se tivermos mais máquinas operando
produziremos mais peças e se tivermos menos máquinas
operando produziremos menos peças. Assim temos que
estas duas grandezas são diretamente proporcionais.
Vamos agora considerar as grandezas Número de peças e
Número de dias. Novamente devemos usar a lógica para
constatar que se tivermos maior número de dias
produziremos maior número de peças e se tivermos menor
número de dias produziremos menor número de peças.
Assim temos que estas duas grandezas também são
diretamente proporcionais.
Concluímos que todas as grandezas envolvidas são
diretamente proporcionais, logo, basta resolver a proporção:
400 5×6
=
x 7×9
que pode ser posta na forma
400 30
=

193. x 63
Resolvendo a proporção, obtemos X=840, assim, se as 7
máquinas funcionarem durante 9 dias serão produzidas 840
peças.
2. Um motociclista, rodando 4h por dia, percorre em média 200
Km em 2 dias. Em quantos dias esse motociclista irá
percorrer 500 Km, se rodar 5 h por dia? (h=hora,
Km=quilômetro).
Vamos representar o número de dias procurado pela letra X.
De acordo com os dados do problema, vamos organizar a
tabela:
Quilômetros (A) Horas por dia (B) No. de dias (C)
200 4 2
500 5 X
A grandeza Número de dias (C) é a que servirá como
referência para as outras grandezas. Analisaremos se as
grandezas Quilômetros (A) e Horas por dia (B) são
diretamente proporcionais ou inversamente proporcionais à
grandeza C que representa o Número de dias. Tal análise
deve ser feita de uma forma independente para cada par de
grandezas.
Consideremos as grandezas Número de dias e Quilômetros.
Usaremos a lógica para constatar que se rodarmos maior
número de dias, percorreremos maior quilometragem e se
rodarmos menor número de dias percorreremos menor
quilometragem. Assim temos que estas duas grandezas são
diretamente proporcionais.
Na outra análise, vamos agora considerar as grandezas
Número de dias e Horas por dia. Verificar que para realizar o
mesmo percurso, se tivermos maior número de dias
utilizaremos menor número de horas por dia e se tivermos

194. menor número de dias necessitaremos maior número de
horas para p mesmo percurso. Logo, estas duas grandezas
são inversamente proporcionais e desse modo:
2 200×5
=
X 500×4
que pode ser posta como
2 1000
=
X 2000
Resolvendo esta proporção, obtemos X=4, significando que
para percorrer 500 Km, rodando 5 h por dia, o motociclista
levará 4 dias.
Porcentagem
Praticamente todos os dias, observamos nos meios de
comunicação, expressões matemáticas relacionadas com
porcentagem. O termo por cento é proveniente do Latim per centum
e quer dizer por cem. Toda razão da forma a/b na qual o
denominador b=100, é chamada taxa de porcentagem ou
simplesmente porcentagem ou ainda percentagem.
Historicamente, a expressão por cento aparece nas principais obras
de aritmética de autores italianos do século XV. O símbolo % surgiu
como uma abreviatura da palavra cento utilizada nas operações
mercantis.
Para indicar um índice de 10 por cento, escrevemos 10% e isto
significa que em cada 100 unidades de algo, tomaremos 10
unidades. 10% de 80 pode ser obtido como o produto de 10% por
80, isto é:
Produto = 10%.80 = 10/100.80 = 800 / 100 = 8

195. Em geral, para indicar um índice de M por cento, escrevemos M% e
para calcular M% de um número N, realizamos o produto:
Produto = M%.N = M.N / 100
Exemplos:
1. Um fichário tem 25 fichas numeradas, sendo que 52%
dessas fichas estão etiquetadas com um número par.
Quantas fichas têm a etiqueta com número par? uantas
fichas têm a etiqueta com número ímpar?
Par = 52% de 25 = 52%.25 = 52.25 / 100 = 13
Nesse fichário há 13 fichas etiquetadas com número par e
12 fichas com número ímpar.
2. Num torneio de basquete, uma determinada seleção
disputou 4 partidas na primeira fase e venceu 3. Qual a
porcentagem de vitórias obtida por essa seleção nessa
fase?
Vamos indicar por X% o número que representa essa
porcentagem. Esse problema pode ser expresso da seguinte
forma:
X% de 4 = 3
Assim:
(X/100).4 = 3
4X/100 = 3
4X = 300
X = 75
Na primeira fase a porcentagem de vitórias foi de 75%.

196. 3. Numa indústria há 255 empregadas. Esse número
corresponde a 42,5% do total de empregados da indústria.
Quantas pessoas trabalham nesse local? Quantos homens
trabalham nessa indústria?
Vamos indicar por X o número total de empregados dessa
indústria. Esse problema pode ser representado por:
42,5% de X = 255
Assim:
42,5%.X = 255
42,5 / 100.X = 255
42,5.X / 100 = 255
42,5.X = 25500
425.X = 255000
X = 255000/425 = 600
Nessa indústria trabalham 600 pessoas, sendo que há 345
homens.
4. Ao comprar uma mercadoria, obtive um desconto de 8%
sobre o preço marcado na etiqueta. Se paguei R$ 690,00
pela mercadoria, qual o preço original dessa mercadoria?
Seja X o preço original da mercadoria. Se obtive 8% de
desconto sobre o preço da etiqueta, o preço que paguei
representa 100%-8%=92% do preço original e isto significa
que
92% de X = 690
logo

197. 92%.X = 690
92/100.X = 690
92.X / 100 = 690
92.X = 69000
X = 69000 / 92 = 750
O preço original da mercadoria era de R$ 750,00.
Juros Simples
Juro é toda compensação em dinheiro que se paga ou se recebe
pela quantia em dinheiro que se empresta ou que é emprestada em
função de uma taxa e do tempo. Quando falamos em juros,
devemos considerar:
1. O dinheiro que se empresta ou que se pede emprestado é
chamado de capital.
2. A taxa de porcentagem que se paga ou se recebe pelo
aluguel do dinheiro é denominada taxa de juros.
3. O tempo deve sempre ser indicado na mesma unidade a que
está submetida a taxa, e em caso contrário, deve-se realizar
a conversão para que tanto a taxa como a unidade de tempo
estejam compatíveis, isto é, estejam na mesma unidade.
4. O total pago no final do empréstimo, que corresponde ao
capital mais os juros, é denominado montante.
Para calcular os juros simples j de um capital C, durante t períodos
com a taxa de i% ao período, basta usar a fórmula:
C·i·t
j=
100
Exemplos:

198. 1. O preço à vista de um aparelho é de R$ 450,00. A loja
oferece este aparelho para pagamento em 5 prestações
mensais e iguais porém, o preço passa a ser de R$ 652,00.
Sabendo-se que a diferença entre o preço à prazo e o preço
à vista é devida aos juros cobrados pela loja nesse período,
qual é a taxa mensal de juros cobrada por essa loja?
A diferença entre os preços dados pela loja é:
652,00 - 450,00 = 202,50
A quantia mensal que deve ser paga de juros é:
202,50 / 5 = 40,50
Se X% é a taxa mensal de juros, então esse problema pode
ser resolvido da seguinte forma:
X% de 450,00 = 40,50
X/100.450,00 = 40,50
450 X / 100 = 40,50
450 X = 4050
X = 4050 / 450
X = 9
A taxa de juros é de 9% ao mês.
2. Uma aplicação feita durante 2 meses a uma taxa de 3% ao
mês, rendeu R$ 1.920,00 de juro. Qual foi o capital
aplicado?
O capital que a aplicaçao rendeu mensalmente de juros foi
de: 1920,00/2=960,00. Se o capital aplicado é indicado por
C, esse problema pode ser expresso por:

199. 3% de C = 960,00
3/100 C = 960,00
3 C / 100 = 960,00
3 C = 96000
C = 96000/3 = 32000,00
O capital aplicado foi de R$ 32.000,00.
15-Ensino Fundamental: Divisão Proporcional
2 partes diret. proporcionais
2 partes direta e inversa
n partes diret. proporcionais
n partes direta e inversa
2 partes invers. proporcionais
Regra de Sociedade
n partes invers. proporcionais
Divisão em duas partes diretamente proporcionais
Para decompor um número M em duas partes A e B diretamente
proporcionais a p e q, montamos um sistema com duas equações e
duas incógnitas, de modo que a soma das partes seja A+B=M, mas
A B
=
p q
A solução segue das propriedades das proporções:
A B A+B M
= = = =K
p q p+q p+q
O valor de K é que proporciona a solução pois:
A=Kp e B=Kq

200. Exemplo: Para decompor o número 100 em duas partes A e B
diretamente proporcionais a 2 e 3, montaremos o sistema de modo
que A+B=100, cuja solução segue de:
A BA+B 100
= = = = 20
2 3 5 5
Segue que A=40 e B=60.
Exemplo: Determinar números A e B diretamente proporcionais a 8
e 3, sabendo-se que a diferença entre eles é 60. Para resolver este
problema basta tomar A-B=60 e escrever:
A B A-B 60
= = = =12
8 3 5 5
Segue que A=96 e B=36.
Divisão em várias partes diretamente proporcionais
Para decompor um número M em partes X1, X2, ..., Xn diretamente
proporcionais a p1, p2, ..., pn, deve-se montar um sistema com n
equações e n incógnitas, sendo as somas X1+X2+...+Xn=M e
p1+p2+...+pn=P.
X1 X2 Xn
= = ... =
p1 p2 pn
A solução segue das propriedades das proporções:
X1 X2 Xn X1+X2+...+Xn M
= =...= = = =K
p1 p2 pn p1+p2+...+pn P

201. Exemplo: Para decompor o número 120 em três partes A, B e C
diretamente proporcionais a 2, 4 e 6, deve-se montar um sistema
com 3 equações e 3 incógnitas tal que A+B+C=120 e 2+4+6=P.
Assim:
A B C A+B+C 120
= = = = =10
2 4 6 P 12
logo A=20, B=40 e C=60.
Exemplo: Determinar números A, B e C diretamente proporcionais a
2, 4 e 6, de modo que 2A+3B-4C=120.
A solução segue das propriedades das proporções:
A B C 2A+3B-4C 120
= = = = = – 15
2 4 6 2×2+3×4-4×6 -8
logo A=-30, B=-60 e C=-90. Também existem proporções com
números negativos! :-)
Divisão em duas partes inversamente proporcionais
Para decompor um número M em duas partes A e B inversamente
proporcionais a p e q, deve-se decompor este número M em duas
partes A e B diretamente proporcionais a 1/p e 1/q, que são,
respectivamente, os inversos de p e q.
Assim basta montar o sistema com duas equações e duas
incógnitas tal que A+B=M. Desse modo:
A B A+B M M.p.q
= = = = =K
1/p 1/q 1/p+1/q 1/p+1/q p+q
O valor de K proporciona a solução pois: A=K/p e B=K/q.

202. Exemplo: Para decompor o número 120 em duas partes A e B
inversamente proporcionais a 2 e 3, deve-se montar o sistema tal
que A+B=120, de modo que:
A B A+B
120 120.2.3
= = = = = 144
1/2 1/3 1/2+1/3 5/6 5
Assim A=72 e B=48.
Exemplo: Determinar números A e B inversamente proporcionais a
6 e 8, sabendo-se que a diferença entre eles é 10. Para resolver
este problema, tomamos A-B=10. Assim:
A B A-B 10
= = = = 240
1/6 1/8 1/6-1/8 1/24
Assim A=40 e B=30.
Divisão em várias partes inversamente proporcionais
Para decompor um número M em n partes X1, X2, ..., Xn
inversamente proporcionais a p1, p2, ..., pn, basta decompor este
número M em n partes X1, X2, ..., Xn diretamente proporcionais a
1/p1, 1/p2, ..., 1/pn.
A montagem do sistema com n equações e n incógnitas, assume
que X1+X2+...+ Xn=M e além disso
X1 X2 Xn
= = ... =
1/p1 1/p2 1/pn
cuja solução segue das propriedades das proporções:
X1 = X2 =...= Xn = X1+X2+...+Xn = M

203. 1/p1 1/p2 1/pn 1/p1+1/p2+...+1/pn 1/p1+1/p2+...+1/pn
Exemplo: Para decompor o número 220 em três partes A, B e C
inversamente proporcionais a 2, 4 e 6, deve-se montar um sistema
com 3 equações e 3 incógnitas, de modo que A+B+C=220. Desse
modo:
A B C A+B+C 220
= = = = = 240
1/2 1/4 1/6 1/2+1/4+1/6 11/12
A solução é A=120, B=60 e C=40.
Exemplo: Para obter números A, B e C inversamente proporcionais
a 2, 4 e 6, de modo que 2A+3B-4C=10, devemos montar as
proporções:
A B C 2A+3B-4C 10 120
= = = = =
1/2 1/4 1/6 2/2+3/4-4/6 13/12 13
logo A=60/13, B=30/13 e C=20/13.
Existem proporções com números fracionários! :-)
Divisão em duas partes direta e inversamente proporcionais
Para decompor um número M em duas partes A e B diretamente
proporcionais a c e d e inversamente proporcionais a p e q, deve-se
decompor este número M em duas partes A e B diretamente
proporcionais a c/q e d/q, basta montar um sistema com duas
equações e duas incógnitas de forma que A+B=M e além disso:
A B A+B M M.p.q
= = = = =K
c/p d/q c/p+d/q c/p+d/q c.q+p.d

204. O valor de K proporciona a solução pois: A=Kc/p e B=Kd/q.
Exemplo: Para decompor o número 58 em duas partes A e B
diretamente proporcionais a 2 e 3, e, inversamente proporcionais a
5 e 7, deve-se montar as proporções:
A B A+B 58
= = = = 70
2/5 3/7 2/5+3/7 29/35
Assim A=(2/5).70=28 e B=(3/7).70=30.
Exemplo: Para obter números A e B diretamente proporcionais a 4 e
3 e inversamente proporcionais a 6 e 8, sabendo-se que a diferença
entre eles é 21. Para resolver este problema basta escrever que A-
B=21 resolver as proporções:
A B A-B 21
= = = = 72
4/6 3/8 4/6-3/8 7/24
Assim A=(4/6).72=48 e B=(3/8).72=27.
Divisão em n partes direta e inversamente proporcionais
Para decompor um número M em n partes X1, X2, ..., Xn diretamente
proporcionais a p1, p2, ..., pn e inversamente proporcionais a q1, q2,
..., qn, basta decompor este número M em n partes X1, X2, ..., Xn
diretamente proporcionais a p1/q1, p2/q2, ..., pn/qn.
A montagem do sistema com n equações e n incógnitas exige que
X1+X2+...+Xn=M e além disso
X1 X2 Xn
= =...=
p1/q1 p2/q2 pn/qn
A solução segue das propriedades das proporções:

205. X1 X2 Xn X1+X2+...+Xn
= =...= =
p1/q1 p2/q2 pn/qn p1/q1+p2/q2+...+pn/qn
Exemplo: Para decompor o número 115 em três partes A, B e C
diretamente proporcionais a 1, 2 e 3 e inversamente proporcionais a
4, 5 e 6, deve-se montar um sistema com 3 equações e 3 incógnitas
de forma de A+B+C=115 e tal que:
A B C A+B+C 115
= = = = = 100
1/4 2/5 3/6 1/4+2/5+3/6 23/20
logo A=(1/4)100=25, B=(2/5)100=40 e C=(3/6)100=50.
Exemplo: Determinar números A, B e C diretamente proporcionais a
1, 10 e 2 e inversamente proporcionais a 2, 4 e 5, de modo que
2A+3B-4C=10.
A montagem do problema fica na forma:
A B C 2A+3B-4C 10 100
= = = = =
1/2 10/4 2/5 2/2+30/4-8/5 69/10 69
A solução é A=50/69, B=250/69 e C=40/69.
Regra de Sociedade
Regra de sociedade é um procedimento matemático que indica a
forma de distribuição de um resultado (lucro ou prejuizo) de uma
sociedade, sendo que os membros poderão participar com capitais
distintos e também em tempos distintos. Os capitais dos membros
participantes são indicados por: C1, C2, ..., Cn e os respectivos
tempos de participação deste capitais da sociedade por t1, t2, ..., tn.

206. Definiremos o peso pk (k=1,2,...,n) de cada participante como o
produto:
pk = Ck tk
e indicaremos o capital total como a soma dos capitais participantes:
C = C1 + C2 + ... + Cn
A Regra de Sociedade é uma aplicação imediata do caso de
decomposição de um valor M diretamente proporcional aos pesos
p1, p2, ..., pn.
Exemplo: Ocorreu a formação de uma sociedade por três pessoas
A, B e C, sendo que A entrou com um capital de R$50.000,00 e nela
permaneceu por 40 meses, B entrou com um capital de
R$60.000,00 e nela permaneceu por 30 meses e C entrou com um
capital de R$30.000,00 e nela permaneceu por 40 meses. Se o
resultado (que pode ser um lucro ou um prejuizo) da empresa após
um certo período posterior, foi de R$25.000,00, quanto deverá
receber (ou pagar) cada sócio?
Os pesos de cada sócio serão indicados em milhares para não
termos muitos zeros nas expressões dos pesos. Desse modo:
p1=50x40=2000; p2=60x30=1800; p 3=30x40=1200
A montagem do problema estabelece que A+B+C=25000 e além
disso:
A B C
= =
2000 1800 1200
A solução segue das propriedades das proporções:
A B C A+B+C 25000
= = = = =5
2000 1800 1200 5000 5000

207. A participação de cada sócio é X=5(2000)=10000, Y=5(1800)=9000
e Z=5(1200)=6000.
16-Ensino Fundamental: Expressões algébricas
O uso das Expressões algébricas Identificando express. algébricas
Elementos históricos Valor numérico expr.algébrica
Expressões Numéricas A regra dos sinais (X e ÷)
Expressões algébricas Regras de potenciação
Prioridade das operações Eliminação de parênteses
Exercícios Operações com expr. algébricas
Monômios e polinômios Alguns Produtos notáveis
O uso das expressões algébricas
No cotidiano, muitas vezes usamos expressões sem perceber que
as mesmas representam expressões algébricas ou numéricas.
Numa papelaria, quando calculamos o preço de um caderno
somado ao preço de duas canetas, usamos expressões como
1x+2y, onde x representa o preço do caderno e y o preço de cada
caneta.
Num colégio, ao comprar um lanche, somamos o preço de um
refrigerante com o preço de um salgado, usando expressoes do tipo
1x+1y onde x representa o preço do salgado e y o preço do
refrigerante.
Usamos a subtração para saber o valor do troco. Por exemplo, se V
é o valor total de dinheiro disponível e T é o valor do troco, então
temos uma expresão algébrica do tipo V-(1x+1y)=T.
As expressões algébricas são encontradas muitas vezes em
fórmulas matemáticas. Por exemplo, no cálculo de áreas de
retângulos, triângulos e outras figuras planas.
Expressão algébrica Objeto matemático Figura
A=bxh Área do retângulo

208. A=bxh/2 Área do triângulo
P=4a Perímetro do quadrado
Elementos históricos
Na Antiguidade, as letras foram pouco usadas na representação de
números e relações. De acordo com fontes históricas, os gregos
Euclides e Aristóteles (322-384 a.C), usaram as letras para
representar números. A partir do século XIII o matemático italiano
Leonardo de Pisa (Fibonacci), que escreveu o livro sobre Liber
Abaci (o livro do ábaco) sobre a arte de calcular, observamos alguns
cálculos algébricos.
O grande uso de letras para resumir mais racionalmente o cálculo
algébrico passou a ser estudado pelo matemático alemão Stifel
(1486-1567), pelos matemáticos italianos Germano (1501-1576) e
Bombelli (autor de Álgebra publicada em 1572), porém, foi com o
matemático francês François Viéte (1540-1603), que introduziu o
uso ordenado de letras nas analogias matemáticas, quando
desenvolveu o estudo do cálculo algébrico.
Expressões Numéricas
São expressões matemáticas que envolvem operações com
números. Por exemplo:
a = 7+5+4
b = 5+20-87
c = (6+8)-10
d = (5×4)+15

209. Expressões algébricas
São expressões matemáticas que apresentam letras e podem
conter números. São também denominadas expressões literais. Por
exemplo:
A = 2a+7b
B = (3c+4)-5
C = 23c+4
As letras nas expressões são chamadas variáveis o que significa
que o valor de cada letra pode ser substituída por um valor
numérico.
Prioridade das operações numa expressão algébrica
Nas operações em uma expressão algébrica, devemos obedecer a
seguinte ordem:
1. Potenciação ou Radiciação
2. Multiplicação ou Divisão
3. Adição ou Subtração
Observações quanto à prioridade:
1. Antes de cada uma das três operações citadas, deve-se
realizar a operação que estiver dentro dos parênteses,
colchetes ou chaves.
2. A multiplicação pode ser indicada por × ou por um ponto · ou
às vezes sem sinal, desde que fique clara a intenção da
expressão.
3. Muitas vezes devemos utilizar parênteses quando
substituímos variáveis por valores negativos.
Exemplos:

210. 1. Consideremos P=2A+10 e tomemos A=5. Assim
2. P = 2.5+10 = 10+10 = 20
Aqui A é a variável da expressão, 5 é o valor numérico da
variável e 20 é o valor numérico da expressão indicada por
P. Observe que ao mudar o valor de A para 9, teremos:
A = 2.9 + 10 = 18 + 10 = 28
Se A=9, o valor numérico de P=2A+10 é igual a 28.
3. Seja X=4A+2+B-7 e tomemos A=5 e B=7. Assim:
4. X = 4.5+2+7-7 = 20+2-0 = 22
Se A=5 e B=7, o valor numérico de X=4A+2+B-7, muda para
22.
5. Seja Y=18-C+9+D+8C, onde C= -2 e D=1. Então:
6. Y = 18-(-2)+9+1+8(-2) = 18+2+9+1-16 = 30-16 =
14
Se C=-2 e D=1, o valor numérico de Y=18-C+9+D+8C, é 14.
Conclusão: O valor numérico de uma expressão algébrica é o valor
obtido na expressão quando substituímos a variável por um valor
numérico.
Exemplos:
1. Um triângulo eqüilátero possui os três lados com mesma
medida. Calcular o perímetro de um triângulo equilátero cujo
lado mede 5 cm, sabendo-se que o perímetro de um
triangulo equilátero pode ser representado por uma
expressão algébrica da forma: P=a+a+a=3a. Substituindo
a=5cm nesta expressão, obtemos P=3×5cm=15cm.

211. 2. Para obter a área do quadrado cujo lado mede 7cm,
devemos usar a expressão algébrica para a área do
quadrado de lado L que é A=L×L=L². Assim, se L=7cm,
então A=7×7=49cm².
Observação: Mudando o valor do lado para L=8cm, o valor
da área mudará para A=8×8=64cm².
3. Escreva expressões algébricas para representar o perímetro
de cada uma das figuras abaixo:
4. Se a letra y representa um número natural, escreva a
expressão algébrica que representa cada um dos seguintes
fatos:
a. O dobro desse número.
b. O sucessor desse número.
c. O antecessor desse número (se existir).
d. Um terço do número somado com seu sucessor.
5. Como caso particular do exercício anterior, tome y=9 e
calcule o valor numérico:
a. do dobro de y
b. do sucessor de y
c. do antecessor de y
d. da terça parte de y somado com o sucessor de y
6. Calcular a área do trapézio ilustrado na figura, sabendo-se
que esta área pode ser calculada pela expressão algébrica

212. A=(B+b)×h/2, onde B é a medida da base maior, b é a
medida da base menor e h é a medida da altura.
Monômios e polinômios
São expressões matemáticas especiais envolvendo valores
numéricos e literais, onde podem aparecer somente operações de
adição, subtração ou multiplicação. Os principais tipos são
apresentados na tabela:
Nome No.termos Exemplo
monômio um m(x,y) = 3 xy
binômio dois b(x,y) = 6 x²y - 7y
trinômio três f(x) = a x² + bx + c
polinômio vários p(x)=aoxn+a1xn-1+a2xn-2+...+an-1x+an
Identificação das expressões algébricas
Com muita frequência, as expressões algébricas aparecem na
forma:
3x²y
onde se observa que ela depende das variáveis literais x e y, mas é
importante identificá-las com nomes como:
p(x,y) = 3x²y
para deixar claro que esta é uma expressão algébrica que depende
das variáveis x e y.
Esta forma de notação é muito útil e nos leva ao conceito de função
de várias variáveis que é um dos conceitos mais importantes da
Matemática.

213. Valor numérico de uma expressão algébrica identificada
É o valor obtido para a expressão, ao substituir as variáveis literais
por valores numéricos.
Exemplo: Tomando p(x,y)=3x²y, então para x=7 e y=2 temos que:
p(7,2) = 3 × 7² × 2 = 294
Se alterarmos os valores de x e de y para x=-1 e y=5, teremos outro
valor numérico:
p(-1,5) = 3 × (-1)² × 5 = 3 × 5 = 15
mas dependendo da mudança de x e de y, poderíamos ter o mesmo
valor numérico que antes. Se x=-7 e y=2, teremos:
p(7,2) = 3 × (-7)² × 2 = 294
A regra dos sinais (multiplicação ou divisão)
(+1) x (+1) = +1 (+1) ÷ (+1) = +1
(+1) x (-1) = -1 (+1) ÷ (-1) = -1
(-1) x (+1) = -1 (-1) ÷ (+1) = -1
(-1) x (-1) = +1 (-1) ÷ (-1) = +1
Regras de potenciação
Para todos os números reais x e y diferentes de zero, e, m e n
números inteiros, tem-se que:
Propriedades Alguns exemplos
xº=1 (x não nulo) 5º = 1
xm xn = xm+n 5².54 = 56
xm ym = (xy)m 5² 3² = 15²

214. xm ÷ xn = xm-n 520 ÷ 54 = 516
xm ÷ ym = (x/y)m 5² ÷ 3² = (5/3)²
(x ) = x
m n mn
(5 )² = 125² = 15625 = 5 6
3
xm÷n = (xm)1/n 53÷2 = (53)1/2 = 1251/2
x-m = 1 ÷ xm 5-3 = 1 ÷ 53 = 1/125
x-m/n = 1 ÷ (xm)1/n 5-3/2 = 1 ÷ (53)1/2= 1 ÷ (125)1/2
Eliminação de parênteses em Monômios
Para eliminar os parênteses em uma expressão algébrica, deve-se
multiplicar o sinal que está fora (e antes) dos parênteses pelo sinal
que está dentro (e antes) dos parênteses com o uso da regra dos
sinais. Se o monômio não tem sinal, o sinal é o positivo. Se o
monômio tem o sinal +, o sinal é o positivo.
Exemplos:
A = -(4x)+(-7x) = -4x-7x = -11x
B = -(4x)+(+7x) = -4x+7x = 3x
C = +(4x)+(-7x) = 4x-7x = - 3x
D = +(4x)+(+7x) = 4x+7x = 11x
Operações com expressões algébricas de Monômios
1. Adição ou Subtração de Monômios
Para somar ou subtrair de monômios, devemos
primeiramente eliminar os parênteses e depois realizar as
operações.
Exemplos:
1. A = -(4x)+(-7x) = -4x-7x = -11x
2. B = -(4x)+(+7x) = -4x+7x = 3x
3. C = +(4x)+(-7x) = 4x-7x = -3x
4. D = +(4x)+(+7x) = 4x+7x = 11x

215. 2. Multiplicação de Monômios
Para multiplicar monômios, deve-se primeiramente
multiplicar os valores numéricos observando com muito
cuidado a regra de multiplicação dos sinais, multiplicar as
potências literais de mesma base e escrever a resposta de
uma forma simplificada:
Exemplos:
1. A = -(4x²y).(-2xy) = +8x³y²
2. B = -(4x²y).(+2xy) = -8x³y²
3. C = +(4x²y).(-2xy) = -8x³y²
4. D = +(4x²y).(+2xy) = +8x³y²
3. Divisão de Monômios
Para dividir monômios, deve-se primeiramente dividir os
valores numéricos observando com muito cuidado a regra de
divisão dos sinais, dividir as potências literais de mesma
base e escrever a resposta de uma forma simplificada:
Exemplos:
1. A = -(4x²y)÷(-2xy) = 2x
2. B = -(4x²y)÷(+2xy) = -2x
3. C = +(4x²y)÷(-2xy) = -2x
4. D = +(4x²y)÷(+2xy) = 2x
4. Potenciação de Monômios
Para realizar a potenciação de um monômio, deve-se
primeiramente realizar a potenciação do valor numérico
levando em consideração o sinal, tomar as potências literais
e escrever a resposta de uma forma simplificada:
Exemplos:
1. A =(+4x²y)³= 4³ x²y x²y ²y = 256 x 6 y³
2. B =(-4x²y)³ = -4³x²y x²y x²y = -256x 6 y³

216. Alguns Produtos notáveis
No link Produtos Notáveis, existem outros trinta (30) produtos
notáveis importantes.
1. Quadrado da soma de dois termos
Sabemos que x²=x.x, y²=y.y, mas não é verdade que
x² + y² = (x+y)²
a menos que um dos dois termos seja nulo. Este é um erro
muito comum, mas o correto é:
(x+y)² = x² + 2xy + y²
Isto significa que o quadrado da soma de dois números sem
sempre é igual à soma dos quadrados desses números.
Existe um algoritmo matemático que permite obter o
quadrado da soma de x e y, e este algoritmo é semelhante
àquele que permite obter o quadrado de um número com
dois dígitos. Por exemplo, o número 13 pode ser
decomposto em 10+3:
x+y 10+3
x+y Compare 10-3
+xy+y² as duas +10.3+3²
x²+xy operações 10²+10.3
x²+2xy+y² 10²+2.10.3+3²
Assim temos que o quadrado da soma de dois termos x e y,
é a soma do quadrado do primeiro termo com o quadrado do
segundo termo e com o dobro do produto do primeiro termo
pelo segundo termo. Em resumo:
(x+y)² = x² + 2xy + y²
Exemplos:

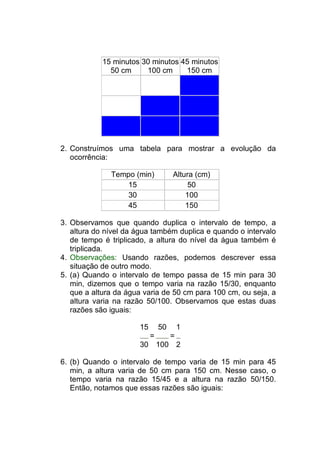
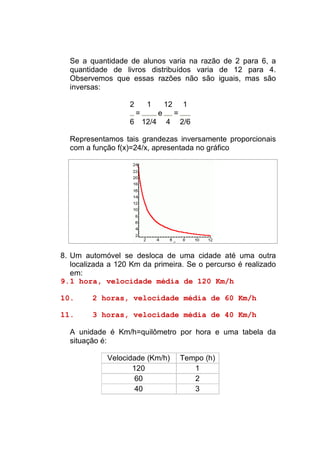
217. (x+8)² = x²+2.x.8+8² = x²+16x+64
(3k+y)² = (3k)²+2.3k.y+y² = 9k²+6ky+y²
(1+x/5)² = 1+ 2x/5 +x²/25
Exercícios: Desenvolver as expressões:
(a+8)² =
(4y+2)² =
(9k/8 +3)² =
Pensando um pouco:
1. Se (x+7)²=x²+[ ]+49, qual é o termo que deve ser
colocado no lugar de [ ]?
2. Se (5a+[ ])² = 25a²+30a+[ ], quais são os termos que
devem ser colocados nos lugares de [ ]?
3. Se ([ ]+9)² = x²+[ ]+81, quais são os termos que
devem ser colocados nos lugares de [ ]?
4. Se (4b+[ ])² = l6b²+36b+[ ], substitua os [ ] por algo
coerente.
5. Se (c+8)²=c²+[ ]+[ ], substitua os [ ] por algo coerente.
2. Quadrado da diferença de dois termos
Como um caso particular da situação anterior, o quadrado
da diferença de x e y é igual ao quadrado de x somado com
o quadrado de y menos duas vezes xy. Resumindo:
(x-y)² = x² - 2xy + y²
Exemplos:
(x-4)² = x²-2.x.4+4² = x²-8x+16
(9-k)² = 9²-2.9.k+k² = 81-18k+k²

218. (2/y -x)² = (2/y)²-2.(2/y).x+x²
Exercícios: Complete o que falta.
(5x-9)² =[ ]
(k-6s)² =[ ]
(p-[ ])² = p²-10p+[ ]
3. Produto da soma pela diferença de dois termos
Vamos utilizar o mesmo algoritmo já usado para o produto
da soma de dois termos.
x+y 10+3
x-y Compare 10-3
-xy-y² as duas -10.3-3²
x²+xy operações 10²+10.3
x² -y² 10² - 3²
Em geral, o produto da soma de x e y pela diferença entre x
e y é igual ao quadrado de x menos o quadrado de y.
(x+y)(x-y) = x² - y²
Exemplos:
(x+2)(x-2) = x²-2x+2x-4 = x²-4
(g-8)(g+8) = g²-8g+8g-64 = g²-64
(k-20)(k+20) = k²-400
(9-z)(9+z) = 81-z²
Exercícios: Complete as expressões:
(6-m)(6+m) =

219. (b+6)(b-6) =
(6+b)(b-6) =
(6+b)(6-b) =
(100-u)(100+u) =
(u-100)(100+u) =
17-Ensino Fundamental: Equações do segundo grau
Introd. às equações algébricas Equaç. incompletas: Exemplos
Fórmula Bhaskara (Sridhara) Solução eq. completas
Equação do segundo grau Uso da fórmula de Bhaskara
Equação completa Exercícios
Equação incompleta Eq. fracionárias
Solução eq. incompletas Equações bi-quadradas
Introdução às equações algébricas
Equações algébricas são equações nas quais a incógnita x está
sujeita a operações algébricas como: adição, subtração,
multiplicação, divisão e radiciação.
Exemplos:
1. a x + b = 0
2. a x² + bx + c = 0
3. a x4 + b x² + c = 0
Uma equação algébrica está em sua forma canônica, quando ela
pode ser escrita como:
ao xn + a1 xn-1 + ... + an-1 x1 + an = 0
onde n é um número inteiro positivo (número natural). O maior
expoente da incógnita em uma equação algébrica é denominado o
grau da equação e o coeficiente do termo de mais alto grau é
denominado coeficiente do termo dominante.

220. Exemplo: A equação 4x²+3x+2=0 tem o grau 2 e o coeficiente do
termo dominante é 4. Neste caso, dizemos que esta é uma equação
do segundo grau.
A fórmula quadrática de Sridhara (Bhaskara)
Mostraremos na sequência como o matemático Sridhara, obteve a
Fórmula (conhecida como sendo) de Bhaskara, que é a fórmula
geral para a resolução de equações do segundo grau. Um fato
curioso é que a Fórmula de Bhaskara não foi descoberta por ele
mas pelo matemático hindu Sridhara, pelo menos um século antes
da publicação de Bhaskara, fato reconhecido pelo próprio Bhaskara,
embora o material construído pelo pioneiro não tenha chegado até
nós.
O fundamento usado para obter esta fórmula foi buscar uma forma
de reduzir a equação do segundo grau a uma do primeiro grau,
através da extração de raízes quadradas de ambos os membros da
mesma.
Seja a equação:
a x² + b x + c = 0
com a não nulo e dividindo todos os coeficientes por a, temos:
x² + (b/a) x + c/a = 0
Passando o termo constante para o segundo membro, teremos:
x² + (b/a) x = -c/a
Prosseguindo, faremos com que o lado esquerdo da equação seja
um quadrado perfeito e para isto somaremos o quadrado de b/2a a
ambos os membros da equação para obter:
x² + (b/a) x + (b/2a)² = -c/a + (b/2a)²
Simplificando ambos os lados da equação, obteremos:

221. [x+(b/2a)]2 = (b² - 4ac) / 4a²
Notação: Usaremos a notação R[x] para representar a raiz quadrada
de x>0. R[5] representará a raiz quadrada de 5. Esta notação está
sendo introduzida aqui para fazer com que a página seja carregada
mais rapidamente, pois a linguagem HTML ainda não permite
apresentar notações matemáticas na Internet de uma forma fácil.
Extraindo a raiz quadrada de cada membro da equação e
lembrando que a raiz quadrada de todo número real não negativo é
também não negativa, obteremos duas respostas para a nossa
equação:
x + (b/2a) = + R[(b²-4ac) / 4a²]
ou
x + (b/2a) = - R[(b²-4ac) / 4a²]
que alguns, por preguiça ou descuido, escrevem:
contendo um sinal ± que é lido como mais ou menos. Lembramos
que este sinal ± não tem qualquer significado em Matemática.
Como estamos procurando duas raízes para a equação do segundo
grau, deveremos sempre escrever:
x' = -b/2a + R[b²-4ac] /2a
ou
x" = -b/2a - R[b²-4ac] /2a
A fórmula de Bhaskara ainda pode ser escrita como:

222. onde D (às vezes usamos a letra maiúscula "delta" do alfabeto
grego) é o discriminante da equação do segundo grau, definido por:
D = b² - 4ac
Equação do segundo grau
Uma equação do segundo grau na incógnita x é da forma:
a x² + b x + c = 0
onde os números reais a, b e c são os coeficientes da equação,
sendo que a deve ser diferente de zero. Essa equação é também
chamada de equação quadrática, pois o termo de maior grau está
elevado ao quadrado.
Equação Completa do segundo grau
Uma equação do segundo grau é completa, se todos os coeficientes
a, b e c são diferentes de zero.
Exemplos:
1. 2 x² + 7x + 5 = 0
2. 3 x² + x + 2 = 0
Equação incompleta do segundo grau
Uma equação do segundo grau é incompleta se b=0 ou c=0 ou
b=c=0. Na equação incompleta o coeficiente a é diferente de zero.
Exemplos:
1. 4 x² + 6x = 0

223. 2. 3 x² + 9 = 0
3. 2 x² = 0
Resolução de equações incompletas do 2o. grau
Equações do tipo ax²=0: Basta dividir toda a equação por a para
obter:
x² = 0
significando que a equação possui duas raízes iguais a zero.
Equações do tipo ax²+c=0: Novamente dividimos toda a equação
por a e passamos o termo constante para o segundo membro para
obter:
x² = -c/a
Se -c/a for negativo, não existe solução no conjunto dos números
reais.
Se -c/a for positivo, a equação terá duas raízes com o mesmo valor
absoluto (módulo) mas de sinais contrários.
Equações do tipo ax²+bx=0: Neste caso, fatoramos a equação para
obter:
x (ax + b) = 0
e a equação terá duas raízes:
x' = 0 ou x" = -b/a
Exemplos gerais
1. 4x²=0 tem duas raízes nulas.
2. 4x²-8=0 tem duas raízes: x'=R[2], x"= -R[2]
3. 4x²+5=0 não tem raízes reais.
4. 4x²-12x=0 tem duas raízes reais: x'=3, x"=0

224. Exercícios: Resolver as equações incompletas do segundo grau.
1. x² + 6x = 0
2. 2 x² = 0
3. 3 x² + 7 = 0
4. 2 x² + 5 = 0
5. 10 x² = 0
6. 9 x² - 18 = 0
Resolução de equações completas do 2o. grau
Como vimos, uma equação do tipo: ax²+bx+c=0, é uma equação
completa do segundo grau e para resolvê-la basta usar a fórmula
quadrática (atribuída a Bhaskara), que pode ser escrita na forma:
onde D=b²-4ac é o discriminante da equação.
Para esse discriminante D há três possíveis situações:
1. Se D<0, não há solução real, pois não existe raiz quadrada
real de número negativo.
2. Se D=0, há duas soluções iguais:
x' = x" = -b / 2a
3. Se D>0, há duas soluções reais e diferentes:
x' = (-b + R[D])/2a
x" = (-b - R[D])/2a
Exemplos: Preencher a tabela com os coeficientes e o discriminante
de cada equação do segundo grau, analisando os tipos de raízes da
equação.

225. Equação a b c Delta Tipos de raízes
x²-6x+8=0 1 -6 8 4 reais e diferentes
x²-10x+25=0
x²+2x+7=0
x²+2x+1=0
x²+2x=0
O uso da fórmula de Bhaskara
Você pode realizar o Cálculo das Raízes da Equação do segundo
grau com a entrada dos coeficientes a, b e c em um formulário,
mesmo no caso em que D é negativo, o que força a existência de
raízes complexas conjugadas. Para estudar estas raízes, visite o
nosso link Números Complexos.
Mostraremos agora como usar a fórmula de Bhaskara para resolver
a equação:
x² - 5 x + 6 = 0
1. Identificar os coeficientes: a=1, b= -5, c=6
2. Escrever o discriminante D = b²-4ac.
3. Calcular D=(-5)²-4×1×6=25-24=1
4. Escrever a fórmula de Bhaskara:
5. Substituir os valores dos coeficientes a, b e c na fórmula:
x' = (1/2)(5+R[1]) = (5+1)/2 = 3
x" = (1/2)(5-R[1]) = (5-1)/2 = 2
Exercícios
1. Calcular o discriminante de cada equação e analisar as
raízes em cada caso:

226. a. x² + 9 x + 8 = 0
b. 9 x² - 24 x + 16 = 0
c. x² - 2 x + 4 = 0
d. 3 x² - 15 x + 12 = 0
e. 10 x² + 72 x - 64 = 0
2. Resolver as equações:
a. x² + 6 x + 9 = 0
b. 3 x² - x + 3 = 0
c. 2 x² - 2 x - 12 = 0
d. 3 x² - 10 x + 3 = 0
Equações fracionárias do segundo grau
São equações do segundo grau com a incógnita aparecendo no
denominador.
Exemplos:
1. 3/(x² - 4) + 1/(x - 3) = 0
2. 3/(x²-4)+1/(x-2)=0
Para resolver este tipo de equação, primeiramente devemos
eliminar os valores de x que anulam os denominadores, uma vez
que tais valores não servirão para as raízes da equação, pois não
existe fração com denominador igual a 0. Na sequência extraímos o
mínimo múltiplo comum de todos os termos dos denominadores das
frações, se houver necessidade.
1. Consideremos o primeiro exemplo:
3/(x² - 4) + 1/(x - 3) = 0
x deve ser diferente de 3, diferente de 2 e diferente de -2,
assim podemos obter o mínimo múltiplo comum entre os
termos como:
MMC(x) = (x² - 4)(x - 3)

227. Reduzindo as frações ao mesmo denominador que deverá
ser MMC(x), teremos:
[3(x-3) + 1(x²-4)] / (x²-4)(x-3) = 0
o que significa que o numerador deverá ser:
3(x - 3) + 1(x² - 4) = 0
que desenvolvido nos dá:
x2 + 3x - 13 = 0
que é uma equação do segundo grau que pode ser resolvida
pela fórmula de Bhaskara. Não existirão números reais
satisfazendo esta equação.
2. Consideremos agora o segundo exemplo:
(x+3)/(2x-1)=2x/(x+4)
O mínimo múltiplo comum entre 2x-1 e x+4 é MMC=(2x-1)(x-
4) (o produto entre estes fatores) e MMC somente se
anulará se x=1/2 ou x= -4. Multiplicando os termos da
equação pelo MMC, teremos uma sequência de expressões
como:
(x+3)(x+4)=2x(2x-1)
x² + 7x + 12 = 4x² - 2x
-3x² + 9x + 12 = 0
3x² - 9x - 12 = 0
x² - 3x - 4 = 0
(x-4)(x+1) = 0
Solução: x'=4 ou x"= -1

228. 3. Estudemos outro exemplo:
3/(x²-4)+1/(x-2)=0
O mínimo múltiplo comum é MMC=x²-4=(x-2)(x+2) e este
MMC somente se anulará se x=2 ou x= -2. Multiplicando os
termos da equação pelo MMC, obteremos:
3 + (x+2)=0
cuja solução é x= -5
Exercícios: Resolver as equações do segundo grau fracionárias:
1. x + 6/x = -7
2. (x+2)/(x+1) = 2x/(x-4)
3. (2-x)/x + 1/x² = 3/x
4. (x+2)/(x-2) + (x-2)/(x+2) = 1
Equações bi-quadradas
São equações do 4o. grau na incógnita x, da forma geral:
a x4 + b x² + c = 0
Na verdade, esta é uma equação que pode ser escrita como uma
equação do segundo grau através da substituição:
y = x²
para gerar
a y² + b y + c = 0
Aplicamos a fórmula quadrática para resolver esta última equação e
obter as soluções y' e y" e o procedimento final deve ser mais
cuidadoso, uma vez que
x² = y' ou x² = y"

229. e se y' ou y" for negativo, as soluções não existirão para x.
Exemplos:
1. Para resolver x4-13x²+36=0, tomamos y=x², para obter y²-
13y+36=0, cujas raízes são y'=4 ou y"=9, assim:
x² = 4 ou x² = 9
o que garante que o conjunto solução é:
S = { 2, -2, 3, -3}
2. Para resolver x4-5x²-36=0, tomamos y=x², para obter y²-5y-
36=0, cujas raízes são y'= -4 ou y"=9 e desse modo:
x² = -4 ou x² = 9
o que garante que o conjunto solução é:
S = {3, -3}
3. Se tomarmos y=x² na equação x4+13x²+36=0, obteremos
y²+13y+36=0, cujas raízes são y'= -4 ou y"= -9 e dessa
forma:
x² = -4 ou x² = -9
o que garante que o conjunto solução é vazio.
18-Ensino Fundamental: Função quadrática (Parábola)
A função quadrática (parábola) O sinal do coeficiente a
Aplicações das parábolas Sinal de Delta e a concavidade
A função quadrática (Parábola)

230. A função quadrática f:R->R é definida por
f(x)=ax²+bx+c
onde a, b e c são constantes reais, sendo que Dom(f)=R, Im(f)=R.
Esta função também é denominada função trinômia do segundo
grau, uma vez que a expressão
a x² + b x + c = 0
representa uma equação trinômia do segundo grau ou
simplesmente uma equação do segundo grau. O gráfico cartesiano
desta função polinomial do segundo grau é uma curva plana
denominada parábola.
Aplicações práticas das parábolas
Dentre as dezenas de aplicações da parábola a situações da vida,
as mais importantes são:
Faróis de carros: Se colocarmos uma lâmpada no foco de um
espelho com a superfície parabólica e esta lâmpada emitir um
conjunto de raios luminosos que venham a refletir sobre o espelho
parabólico do farol, os raios refletidos sairão todos paralelamente ao
eixo que contem o "foco" e o vértice da superfície parabólica. Esta é
uma propriedade geométrica importante ligada à Ótica, que permite
valorizar bastante o conceito de parábola no âmbito do Ensino
Fundamental.

231. Antenas parabólicas: Se um satélite artificial colocado em uma
órbita geoestacionária emite um conjunto de ondas
eletromagnéticas, estas poderão ser captadas pela sua antena
parabólica , uma vez que o feixe de raios atingirá a sua antena que
tem formato parabólico e ocorrerá a reflexão desses raios
exatamente para um único lugar, denominado o foco da parábola,
onde estará um aparelho de receptor que converterá as ondas
eletromagnéticas em um sinal que a sua TV poderá transformar em
ondas que por sua vez significarão filmes, jornais e outros
programas que você assiste normalmente.
Radares: Os radares usam as propriedades óticas da parábola,
similares às citadas anteriormente para a antena parabólica e para
os faróis.
Lançamentos de projéteis: Ao lançar um objeto no espaço (dardo,
pedra, tiro de canhão) visando alcançar a maior distância possível
tanto na horizontal como na vertical, a curva descrita pelo objeto é
aproximadamente uma parábola, se considerarmos que a
resistência do ar não existe ou é pequena.

232. Sob estas circunstâncias o ângulo de maior alcance horizontal é de
45 graus.
O sinal do coeficiente do termo dominante
O sinal do coeficiente do termo dominante desta função polinomial
indica a concavidade da parábola ("boca aberta"). Se a>0 então a
concavidade estará voltada para cima e se a<0 estará voltada para
baixo.
Exemplo: A parábola, que é o gráfico da função f(x)=x²+2x-3, pode
ser vista no desenho.
O modo de construir esta parábola é atribuir valores para x e obter
os respectivos valores para f(x). A tabela a seguir mostra alguns
pares ordenados de pontos do plano cartesiano onde a curva
deverá passar:
x -3 -2-1 0 1 2
f(x) 0 -3-4 -3 0 5
Como a>0, a concavidade ("boca") da nossa parábola estará
voltada para cima.
Exemplo: Construir a parábola f(x)=-x²+2x-3.

233. Este exemplo é análogo ao anterior, só que nesse caso, a<0, logo
sua concavidade será voltada para baixo. A diferença entre esta
parábola e a do exemplo anterior é que, houve a mudança do sinal
do coeficiente do termo dominante. A construção da tabela nos dá:
x -1 0 1 2 3
f(x) -6 -3 -2 -3 -6
Relacionamento entre o discriminante e a concavidade
Podemos construir uma tabela que relaciona o sinal do
discriminante com o sinal do coeficiente do termo dominante da
função polinomial.
a>0 a<0
A parábola no plano concavidade concavidade
Delta
cartesiano (boca) para (boca) para
cima baixo
D > Corta o eixo horizontal em 2
0 pontos
D= Toca em 1 ponto do eixo
0 horizontal
D<
Não corta o eixo horizontal
0

234. Exercícios: Construir o gráfico cartesiano de cada uma das funções
do segundo grau:
a. f(x) = x²-3x-4
b. f(x) = -3x²+5x-8
c. f(x) = 4x²-4x+1
Máximos e mínimos com funções quadráticas
Existem muitas aplicações para a função quadrática e uma delas
está relacionada com a questão de máximos e mínimos.
Exemplo: Determinar o retângulo de maior área que é possível
construir se o seu perímetro mede 36 m.
Solução: Se x é a medida do comprimento e y é a medida da
largura, a área será dada por: A(x,y)=xy, mas acontece que
2x+2y=36 ou seja x+y=18, assim:
A(x) = x(18-x)
Esta parábola corta o eixo OX nos pontos x=0 e x=18 e o ponto de
máximo.