63161537 matematica

Apostilas Aprendizado Urbano
MATEMÁTICAMATEMÁTICAMATEMÁTICAMATEMÁTICA
1. Teoria dos conjuntos. Conjuntos numéricos. Relações. Funções e equações polinomiais e transcendentais
(exponenciais, logarítmicas e trigonométricas).
2. Análise combinatória, progressão aritmética, progressão geométrica e probabilidade básica.
3. Matrizes, determinantes e sistemas lineares.
4. Geometria plana: Áreas e perímetros.
5. Geometria espacial: áreas e volumes.
6. Números complexos.
7. Estatística básica.
8. Matemática financeira.
9. Aritmética.

Teoria dos conjuntosTeoria dos conjuntosTeoria dos conjuntosTeoria dos conjuntos
Conjunto: representa uma coleção de objetos.
a. O conjunto de todos os brasileiros.
b. O conjunto de todos os números naturais.
c. O conjunto de todos os números reais tal que x²-4=0.
Em geral, um conjunto é denotado por uma letra maiúscula do alfabeto: A, B, C, ..., Z.
Elemento: é um dos componentes de um conjunto.
a. José da Silva é um elemento do conjunto dos brasileiros.
b. 1 é um elemento do conjunto dos números naturais.
c. -2 é um elemento do conjunto dos números reais que satisfaz à equação x²-4=0.
Em geral, um elemento de um conjunto, é denotado por uma letra minúscula do alfabeto: a, b, c, ..., z.
Pertinência: é a característica associada a um elemento que faz parte de um conjunto.
a. José da Silva pertence ao conjunto dos brasileiros.
b. 1 pertence ao conjunto dos números naturais.
c. -2 pertence ao conjunto de números reais que satisfaz à equação x²-4=0.
Símbolo de pertinência: Se um elemento pertence a um conjunto utilizamos o símbolo que se lê:
"pertence".
Para afirmar que 1 é um número natural ou que 1 pertence ao conjunto dos números naturais, escrevemos:
1 N
Para afirmar que 0 não é um número natural ou que 0 não pertence ao conjunto dos números naturais,
escrevemos:
0 N
Um símbolo matemático muito usado para a negação é a barra / traçada sobre o símbolo normal.
Algumas notações para conjuntos
Muitas vezes, um conjunto é representado com os seus elementos dentro de duas chaves { e } através de
duas formas básicas e de uma terceira forma geométrica:
Apresentação: Os elementos do conjunto estão dentro de duas chaves { e }.
a. A={a,e,i,o,u}
b. N={1,2,3,4,...}
c. M={João,Maria,José}
Descrição: O conjunto é descrito por uma ou mais propriedades.

a. A={x: x é uma vogal}
b. N={x: x é um número natural}
c. M={x: x é uma pessoa da família de Maria}
Diagrama de Venn-Euler: (lê-se: "Ven-óiler") Os conjuntos são mostrados graficamente.
Subconjuntos
Dados os conjuntos A e B, diz-se que A está contido em B, denotado por A B, se todos os
elementos de A também estão em B. Algumas vezes diremos que um conjunto A está propriamente contido
em B, quando o conjunto B, além de conter os elementos de A, contém também outros elementos. O
conjunto A é denominado subconjunto de B e o conjunto B é o superconjunto que contém A.
Alguns conjuntos especiais
Conjunto vazio: É um conjunto que não possui elementos. É representado por { } ou por Ø. O conjunto
vazio está contido em todos os conjuntos.
Conjunto universo: É um conjunto que contém todos os elementos do contexto no qual estamos
trabalhando e também contém todos os conjuntos desse contexto. O conjunto universo é representado por
uma letra U. Na sequência não mais usaremos o conjunto universo.
Reunião de conjuntos
A reunião dos conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A ou ao
conjunto B.
A B = { x: x A ou x B }
Exemplo: Se A={a,e,i,o} e B={3,4} então A B={a,e,i,o,3,4}.
Interseção de conjuntos
A interseção dos conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A e ao
conjunto B.
A B = { x: x A e x B }
Exemplo: Se A={a,e,i,o,u} e B={1,2,3,4} então A B=Ø.

Quando a interseção de dois conjuntos A e B é o conjunto vazio, dizemos que estes conjuntos são disjuntos.
Propriedades dos conjuntos
1. Fechamento: Quaisquer que sejam os conjuntos A e B, a reunião de A e B, denotada por A
B e a interseção de A e B, denotada por A B, ainda são conjuntos no universo.
2. Reflexiva: Qualquer que seja o conjunto A, tem-se que:
A A = A e A A = A
3. Inclusão: Quaisquer que sejam os conjuntos A e B, tem-se que:
A A B, B A B, A B A, A
B B
4. Inclusão relacionada: Quaisquer que sejam os conjuntos A e B, tem-se que:
A B equivale a A B = B
A B equivale a A B = A
5. Associativa: Quaisquer que sejam os conjuntos A, B e C, tem-se que:
A (B C) = (A B) C
A (B C) = (A B) C
6. Comutativa: Quaisquer que sejam os conjuntos A e B, tem-se que:
A B = B A
A B = B A
7. Elemento neutro para a reunião: O conjunto vazio Ø é o elemento neutro para a reunião de
conjuntos, tal que para todo conjunto A, se tem:
A Ø = A
8. Elemento "nulo" para a interseção: A interseção do conjunto vazio Ø com qualquer outro conjunto
A, fornece o próprio conjunto vazio.

A Ø = Ø
9. Elemento neutro para a interseção: O conjunto universo U é o elemento neutro para a interseção de
conjuntos, tal que para todo conjunto A, se tem:
A U = A
10.Distributiva: Quaisquer que sejam os conjuntos A, B e C, tem-se que:
A (B C ) = (A B) (A C)
A (B C) = (A B) (A C)
Os gráficos abaixo mostram a distributividade.
Diferença de conjuntos
A diferença entre os conjuntos A e B é o conjunto de todos os elementos que pertencem ao conjunto A e
não pertencem ao conjunto B.
A-B = {x: x A e x B}
Do ponto de vista gráfico, a diferença pode ser vista como:
Complemento de um conjunto
O complemento do conjunto B contido no conjunto A, denotado por CAB, é a diferença entre os conjuntos
A e B, ou seja, é o conjunto de todos os elementos que pertencem ao conjunto A e não pertencem ao
conjunto B.
CAB = A-B = {x: x A e x B}
Graficamente, o complemento do conjunto B no conjunto A, é dado por:
Quando não há dúvida sobre o universo U em que estamos trabalhando, simplesmente utilizamos a letra c
posta como expoente no conjunto, para indicar o complemento deste conjunto. Muitas vezes usamos a
palavra complementar no lugar de complemento.
Exemplos: Øc=U e Uc=Ø.

Leis de Augustus De Morgan
1. O complementar da reunião de dois conjuntos A e B é a interseção dos complementares desses
conjuntos.
(A B)c = Ac Bc
2. O complementar da reunião de uma coleção finita de conjuntos é a interseção dos complementares
desses conjuntos.
(A1 A2 ... An)c = A1c A2c ...
Anc
3. O complementar da interseção de dois conjuntos A e B é a reunião dos complementares desses
conjuntos.
(A B)c = Ac Bc
4. O complementar da interseção de uma coleção finita de conjuntos é a reunião dos complementares
desses conjuntos.
(A1 A2 ... An)c = A1c A2c ...
Anc
Diferença simétrica
A diferença simétrica entre os conjuntos A e B é o conjunto de todos os elementos que pertencem à reunião
dos conjuntos A e B e não pertencem à interseção dos conjuntos A e B.
A B = { x: x A B e x A B }
O diagrama de Venn-Euler para a diferença simétrica é:
Exercício: Dados os conjuntos A, B e C, pode-se mostrar que:
1. A=Ø se, e somente se, B=A B.
2. O conjunto vazio é o elemento neutro para a operação de diferença simétrica. Usar o ítem anterior.
3. A diferença simétrica é comutativa.
4. A diferença simétrica é associativa.
5. A A=Ø (conjunto vazio).
6. A interseção entre A e B C é distributiva, isto é:
A (B C) = (A B) (A C)

7. A B está contida na reunião de A C e de B C, mas esta inclusão é própria, isto é:
A B (A C) (B C)
Conjunto dos Números Naturais
São todos os números inteiros positivos, incluindo o zero. É representado pela letra maiúscula N.
Caso queira representar o conjunto dos números naturais não-nulos (excluindo o zero), deve-se colocar um
* ao lado do N:
N = {0,1,2,3,4,5,6,7,8,9,10, …}
N* = {1,2,3,4,5,6,7,8,9,10,11, …}
Conjunto dos Números Inteiros
São todos os números que pertencem ao conjunto dos Naturais mais os seus respectivos opostos (negativos).
São representados pela letra Z:
Z = {… -4, -3, -2, -1, 0, 1, 2, 3, 4, …}
O conjunto dos inteiros possui alguns subconjuntos, eles são:
- Inteiros não negativos
São todos os números inteiros que não são negativos. Logo percebemos que este conjunto é igual ao
conjunto dos números naturais.
É representado por Z+:
Z+ = {0,1,2,3,4,5,6, …}
- Inteiros não positivos
São todos os números inteiros que não são positivos. É representado por Z-:
Z- = {…, -5, -4, -3, -2, -1, 0}
- Inteiros não negativos e não-nulos
É o conjunto Z+ excluindo o zero. Representa-se esse subconjunto por Z*+:
Z*+ = {1, 2, 3, 4, 5, 6, 7, …}
Z*+ = N*
- Inteiros não positivos e não nulos
São todos os números do conjunto Z- excluindo o zero. Representa-se por Z*-.
Z*- = {… -4, -3, -2, -1}
Conjunto dos Números Racionais
Os números racionais é um conjunto que engloba os números inteiros (Z), números decimais finitos (por
exemplo, 743,8432) e os números decimais infinitos periódicos (que repete uma sequência de algarismos da
parte decimal infinitamente), como “12,050505…”, são também conhecidas como dízimas periódicas.
Os racionais são representados pela letra Q.
Conjunto dos Números Irracionais
É formado pelos números decimais infinitos não-periódicos. Um bom exemplo de número irracional é o
número PI (resultado da divisão do perímetro de uma circunferência pelo seu diâmetro), que vale
3,14159265 …. Atualmente, supercomputadores já conseguiram calcular bilhões de casas decimais para o

PI.
Também são irracionais todas as raízes não exatas, como a raiz quadrada de 2 (1,4142135 …)
Conjunto dos Números Reais
É formado por todos os conjuntos citados anteriormente (união do conjunto dos racionais com os
irracionais).
Representado pela letra R.
Relações e Funções
A função polinomial
Um polinômio (função polinomial) com coeficientes reais na variável x é uma função matemática f:R
R definida por:
p(x) = ao + a1x + a2x² + a3x³ +...+ anxn
onde ao, a1, a2, ..., an são números reais, denominados coeficientes do polinômio. O coeficiente ao é o
termo constante.
Se os coeficientes são números inteiros, o polinômio é denominado polinômio inteiro em x.
Uma das funções polinomiais mais importantes é f:R R definida por:
f(x) = a x² + b x + c
O gráfico desta função é a curva plana denominada parábola, que tem algumas características utilizadas em
estudos de Cinemática, radares, antenas parabólicas e faróis de carros.
O valor numérico de um polinômio p=p(x) em x=a é obtido pela substituição de x pelo número a, para obter
p(a).
Exemplo: O valor numérico de p(x)=2x²+7x-12 para x=3 é dado por:
p(3) = 2×(3)²+7×3-12 = 2×9+21-12 = 18+9 = 27
Grau de um polinômio
Em um polinômio, o termo de mais alto grau que possui um coeficiente não nulo é chamado termo
dominante e o coeficiente deste termo é o coeficiente do termo dominante. O grau de um polinômio p=p(x)
não nulo, é o expoente de seu termo dominante, que aqui será denotado por gr(p).

Acerca do grau de um polinômio, existem várias observações importantes:
1. Um polinômio nulo não tem grau uma vez que não possui termo dominante. Em estudos mais
avançados, define-se o grau de um polinômio nulo mas não o faremos aqui.
2. Se o coeficiente do termo dominante de um polinômio for igual a 1, o polinômio será chamado
mônico.
3. Um polinômio pode ser ordenado segundo as suas potências em ordem crescente ou decrescente.
4. Quando existir um ou mais coeficientes nulos, o polinômio será dito incompleto.
5. Se o grau de um polinômio incompleto for n, o número de termos deste polinômio será menor do
que n+1.
6. Um polinômio será completo quando possuir todas as potências consecutivas desde o grau mais alto
até o termo constante.
7. Se o grau de um polinômio completo for n, o número de termos deste polinômio será exatamente
n+1.
É comum usar apenas uma letra p para representar a função polinomial p=p(x) e P[x] o conjunto de todos os
polinômios reais em x.
Igualdade de polinômios
Os polinomios p e q em P[x], definidos por:
p(x) = ao + a1x + a2x² + a3x³ +...+ anxn
q(x) = bo + b1x + b2x² + b3x³ +...+ bnxn
são iguais se, e somente se, para todo k=0,1,2,3,...,n:
ak=bk
Teorema: Uma condição necessária e suficiente para que um polinômio inteiro seja identicamente nulo é
que todos os seus coeficientes sejam nulos.
Assim, um polinômio:
p(x) = ao + a1x + a2x² + a3x³ +...+ anxn
será nulo se, e somente se, para todo k=0,1,2,3,...,n:
ak= 0
O polinômio nulo é denotado por po=0 em P[x].
O polinômio unidade (identidade para o produto) p1=1 em P[x], é o polinômio:
p(x) = ao + a1x + a2x² + a3x³ + ...+ anxn
tal que ao=1 e ak=0, para todo k=1,2,3,...,n.
Soma de polinômios
Consideremos p e q polinômios em P[x], definidos por:

p(x) = ao + a1x + a2x² + a3x³ +... + anxn
q(x) = bo + b1x + b2x² + b3x³ +... + bnxn
Definimos a soma de p e q, por:
(p+q)(x) = (ao+bo)+(a1+b1)x+(a2+b2)x²+...+(an+bn)xn
A estrutura matemática (P[x],+) formada pelo conjunto de todos os polinômios com a soma definida acima,
possui algumas propriedades:
Associativa: Quaisquer que sejam p, q, r em P[x], tem-se que:
(p + q) + r = p + (q + r)
Comutativa: Quaisquer que sejam p, q em P[x], tem-se que:
p + q = q + p
Elemento neutro: Existe um polinômio po(x)=0 tal que
po + p = p
qualquer que seja p em P[x].
Elemento oposto: Para cada p em P[x], existe outro polinômio q=-p em P[x] tal que
p + q = 0
Com estas propriedades, a estrutura (P[x],+) é denominada um grupo comutativo.
Produto de polinômios
Sejam p, q em P[x], dados por:
p(x) = ao + a1x + a2x² + a3x³ +...+ anxn
q(x) = bo + b1x + b2x² + b3x³ +...+ bnxn
Definimos o produto de p e q, como um outro polinômio r em P[x]:
r(x) = p(x)·q(x) = co + c1x + c2x² + c3x³ +...+ cnxn
tal que:
ck = aobk + a1bk-1 + a2 bk-2 + a3bk-3 +...+ ak-1 b1 + akbo
para cada ck (k=1,2,3,...,m+n). Observamos que para cada termo da soma que gera ck, a soma do índice de a
com o índice de b sempre fornece o mesmo resultado k.
A estrutura matemática (P[x],·) formada pelo conjunto de todos os polinômios com o produto definido
acima, possui várias propriedades:
Associativa: Quaisquer que sejam p, q, r em P[x], tem-se que:
(p · q) · r = p · (q · r)
Comutativa: Quaisquer que sejam p, q em P[x], tem-se que:
p · q = q · p
Elemento nulo: Existe um polinômio po(x)=0 tal que

po · p = po
qualquer que seja p em P[x].
Elemento Identidade: Existe um polinômio p1(x)=1 tal que
p1 · p = p
qualquer que seja p em P[x]. A unidade polinomial é simplesmente denotada por p1=1.
Existe uma propriedade mista ligando a soma e o produto de polinômios
Distributiva: Quaisquer que sejam p, q, r em P[x], tem-se que:
p · (q + r) = p · q + p · r
Com as propriedades relacionadas com a soma e o produto, a estrutura matemática (P[x],+,·) é denominada
anel comutativo com identidade.
Espaço vetorial dos polinômios reais
Embora uma sequência não seja um conjunto mas sim uma função cujo domínio é o conjunto dos números
naturais, usaremos neste momento uma notação para sequência no formato de um conjunto.
O conjunto P[x] de todos os polinômios pode ser identificado com o conjunto S das sequências quase-nulas
de números reais , isto é, as sequências da forma:
p = (ao,a1,a2,a3,a4,...,an,0,0,0,...)
Isto significa que após um certo número natural n, todos os termos da sequência são nulos.
A identificação ocorre quando tomamos os coeficientes do polinômio
p(x) = ao + a1x + a2x² + a3x³ +...+ anxn
e colocamos os mesmos entre parênteses e após o n-ésimo coeficiente colocamos uma quantidade infinita de
zeros, assim nós temos somente uma quantidade finita de números não nulos, razão pela qual tais
sequências são denominadas sequências quase-nulas.
Esta forma de notação
p = (ao,a1,a2,a3,a4,...,an,0,0,0,...)
funciona bem quando trabalhamos com espaços vetoriais, que são estruturas matemáticas onde a soma dos
elementos e a multiplicação dos elementos por escalar têm várias propriedades.
Vamos considerar S o conjunto das sequências quase-nulas de números reais com as operações de soma,
multiplicação por escalar e de multiplicação, dadas abaixo.
Sejam p e q em S, tal que:
p = (ao,a1,a2,a3,a4,...,am,0,0,0,...)
q = (bo,b1,b2,b3,b4,...,bn,0,0,0,...)
e vamos supor que m < n.
Definimos a soma de p e q, como:
p+q = (ao+bo,a1+b1,a2+b2,...,an+bn,0,0,0,...)

a multiplicação de p em S por um escalar k, como:
k.p = (kao,ka1,ka2,ka3,ka4,...,kam,0,0,...)
e o produto de p e q em S como:
p·q = (co,c1,c2,c3,c4,...,cn,0,0,0,...)
sendo que
ck = aobk + a1bk-1 + a2bk-2 + a3bk-3 +...+ ak-1b1+akbo
para cada ck (k=1,2,3,...,m+n).
O conjunto S com as operações definidas é: associativo, comutativo, distributivo e possui elementos: neutro,
identidade, unidade, oposto.
Características do grau de um polinômio
Se gr(p)=m e gr(q)=n então
gr(p.q) = gr(p) + gr(q)
gr(p+q)<max{gr(p),gr(q)}
Algoritmo da divisão de polinômios
Dados os polinômios p e q em P[x], dizemos que q divide p se existe um polinômio g em P[x] tal que
p(x) = g(x) q(x)
Se p em P[x] é um polinômio com gr(p)=n e g é um outro polinômio com gr(g)=m<n, então existe um
polinômio q em P[x] e um polinômio r em P[x] com gr(r)<gr(g), tal que:
p(x) = q(x) g(x) + r(x)
Um caso particular importante é quando tomamos g(x)=x-c e
p(x) = ao + a1x + a2x² + a3x³ +...+ anxn
Como para todo k=1,2,3,...,n vale a identidade:
xk-ck = (x-c)( xk-1 + cxk-2 + c²xk-3 +...+ ck-2x+ck-1 )
então para
p(x) = ao + a1x + a2x² + a3x³ +...+ anxn
temos que
p(c) = ao + a1c + a2c² + a3c³ +...+ ancn
e tomando a diferença entre p(x) e p(c), teremos:
p(x)-p(c) = a1(x-c) + a2(x²-c²) + a3(x³-c³) +...+ an(xn-cn)
o que garante que podemos evidenciar g(x)=x-c para obter
p(x)- p(c)=(x-c) q(x)
onde q=q(x) é um polinômio de grau n-1. Assim, podemos escrever:

p(x)=(x-c) q(x)+p(c)
e é claro que r(x)=p(c) é um polinômio de grau 0.
Zeros de um polinômio
Um zero de um polinômio real p em P[x] é um número c, que pode ser real ou complexo, tal que p(c)=0. O
zero de um polinômio também é denominado raiz do polinômio.
Uma consequência do Algoritmo da Divisão de polinômios é que:
x-c é um fator de p se, e somente se, r(x)=f(c)=0
o que é equivalente a:
c é um zero de p, sse, x-c é um divisor de p=p(x)
Equações Algébricas e Transcendentes
Uma equação algébrica real na variável x é uma relação matemática que envolve apenas um número finito
de operações de soma, subtração, produto, divisão e radiciação de termos envolvendo a variável x.
Exemplos
1. 2x²+3x+7=0
2. 3x²+7x½=2x+3
A função exponencial exp(x)=ex pode ser escrita como um somatório com infinitos termos contendo
potências de x:
ex = 1 + x +x²/2! + x³/3! + x4/4! + x5/5! +...
assim, a equação
x²+7x=ex
não é uma equação algébrica, o que equivale a dizer que esta equação é transcendente.
Quando a equação é da forma:
p(x) = 0
onde p é um polinômio real em P[x], ela será chamada equação polinomial.
Quando uma equação possui a variável sob um sinal de radiciação ela é chamada equação irracional.
Exemplo: 2x²+3x+7 =0 e 3x²+7x½=2x+3 são equações algébricas. A primeira é polinomial, mas a segunda
não é polinomial. Esta segunda é uma equação irracional.
Observação: Uma equação algébrica irracional sempre poderá ser colocada na forma de uma equação
polinomial. Quando uma equação algébrica irracional é transformada em uma equação polinomial, as raízes
da nova equação poderão não coincidir com as raízes da equação original e as raízes obtidas desta nova
equação que não servem para a equação original são denominadas raízes estranhas.
Exercício: Apresentar uma equação irracional que tenha raízes estranhas.

Métodos de resolução algébrica
Alguns tipos especiais de equações podem ser resolvidos.
Equação do 1o. grau: A equação ax+b=0 com a diferente de zero, admite uma única raíz dada por:
x = -b/a
Equação do 2o. grau: A equação ax²+bx+c=0 com a diferente de zero, admite exatamente duas raízes no
conjunto dos números complexos, dadas por:
x1=(-b+R[b²-4ac] / 2a
x2=(-b- R[b²-4ac]/ 2a
onde R[z] é a raiz quadrada de z.
Equação cúbica: A equação ax³+bx²+cx+d=0 com a não nulo, admite exatamente três raízes no conjunto dos
números complexos que podem ser obtidas pela fórmula de Tartaglia (Cardano).
Equação quártica: A equação ax4+bx³+cx²+dx+e=0 com a não nulo, admite exatamente quatro raízes no
conjunto dos números complexos que podem ser obtidas pela fórmula de Ferrari.
Equação quíntica: Para equações de grau maior ou igual a 5, não existem métodos algébricos para obter
todas as raízes, mas existem muitos métodos numéricos que proporcionam as raízes de tais equações com
grande precisão.
Existe uma versão da planilha Kyplot disponível gratuitamente na Internet, que dispõe de um mecanismo
capaz de calcular com grande precisão raízes de equações polinomiais de grau n.
Em Português, há um excelente livro que trata sobre Equações Algébricas e a história da Matemática
subjacente: "O Romance das Equações Algébricas, Gilberto G. Garbi, Makron Books, São Paulo, 1999."
Teorema Fundamental da Álgebra
Teorema (Gauss): Toda equação algébrica polinomial com coeficientes reais ou complexos, admite no
conjunto dos números complexos, pelo menos uma raiz.
Teorema equivalente: Toda equação algébrica polinomial de grau n, com coeficientes reais ou complexos,
admite exatamente n raízes, no conjunto dos números complexos.
Consequência: Toda equação algébrica polinomial real de grau n, admite no máximo n raízes, no conjunto
dos números reais.
Algumas identidades polinomiais
Algumas desigualdades polinomiais
Algumas desigualdades bastante comuns que podem ser obtidas a partir das identidades polinomiais:

1. a²+b² > 2ab
2. (a+b)/2 > R[a.b]
3. a²+b²+c² > ab+ac+bc
onde R[x] é a raiz quadrada de x e o símbolo > significa maior ou igual.
A função exponencial
A função exponencial natural é a função exp:R R+, definida como a inversa da função logarítmo
natural, isto é:
Ln[exp(x)]=x, exp[Ln(x)]=x
O gráfico da função exponencial é obtido pela reflexão do gráfico da função Logaritmo natural em relação à
identidade dada pela reta y=x.
Como o domínio da função Logaritmo natural é o conjunto dos números reais positivos, então a imagem da
função exp é o conjunto dos números reais positivos e como a imagem de Ln é o conjunto R de todos os
números reais, então o domínio de exp também é o conjunto R de todos os números reais.
Observação: Através do gráfico de f(x)=exp(x), observamos que:
1. exp(x)>0 se x é real)
2. 0<exp(x)<1 se x<0
3. exp(x)=1 se x=0
4. exp(x)>1 se x>0
No Ensino Médio, a função exponencial é definida a partir da função logarítmica e ciclicamente define-se a
função logarítmica em função da exponencial como:
f(x)=exp(x), se e somente se, x=Ln(y)
Para uma definição mais cuidadosa, veja Logaritmos.
Exemplos:
1. Ln[exp(5)]=5
2. exp[ln(5)]=5
3. Ln[exp(x+1)1/2]=(x+1)1/2
4. exp[Ln((x+1)1/2]=(x+1)1/2
5. exp[3.Ln(x)]=exp(Ln(x³)]=x³
6. exp[k.Ln(x)]=exp[Ln(xk)]=xk
7. exp[(7(Ln(3)-Ln(4)]=exp[7(Ln(3/4))]=exp[(Ln(3/4)]7)=(3/4)7

A Constante e de Euler
Existe uma importantíssima constante matemática definida por
e = exp(1)
O número e é um número irracional e positivo e em função da definição da função exponencial, temos que:
Ln(e)=1
Este número é denotado por e em homenagem ao matemático suíço Leonhard Euler (1707-1783), um dos
primeiros a estudar as propriedades desse número.
O valor deste número expresso com 40 dígitos decimais, é:
e=2,718281828459045235360287471352662497757
Conexão entre o número e e a função exponencial
Se x é um número real, a função exponencial exp(.) pode ser escrita como a potência de base e com
expoente x, isto é:
ex = exp(x)
Significado geométrico de e
Tomando um ponto v do eixo OX, com v>1 tal que a área da região do primeiro quadrante localizada sob a
curva y=1/x e entre as retas x=1 e x=v seja unitária, então o valor de v será igual a e.
Propriedades básicas da função exponencial
Se x e y são números reais e k é um número racional, então:
1. y=exp(x) se, e somente se, x=Ln(y).
2. exp[Ln(y)]=y para todo y>0.
3. Ln[exp(x)]=x para todo x real.
4. exp(x+y)=exp(x) exp(y)
5. exp(x-y)=exp(x)/exp(y)
6. exp(x.k)=[exp(x)]k
Simplificações matemáticas
Podemos simplificar algumas expressões matemáticas com as propriedades das funções exponenciais e
logaritmos:
1. exp[Ln(3)]=3.

2. Ln[exp(20x)]=20x.
3. exp[5.Ln(2)]=exp[Ln(25)]=25=32.
4. exp[2+5.ln(2)]=exp(2)exp(5.Ln(2))=32e².
Outras funções exponenciais
Podemos definir outras funções exponenciais como g(x)=ax, onde a é um número real positivo diferente de
1 e de x. Primeiro, consideremos o caso onde o expoente é um número racional r.
Tomando x=ar na equação x=exp[Ln(x)], obtemos:
ar=exp[Ln(ar)]
Como Ln[ar]=r.Ln(a), a relação acima fica na forma:
ar = exp[r.Ln(a)]
Esta última expressão, juntamente com a informação que todo número real pode ser escrito como limite de
uma sequência de números racionais, justifica a definição para g(x)=ax, onde x é um número real:
ax=exp[x.Ln(a)]
Leis dos expoentes
Se x e y são números reais, a e b são números reais positivos, então:
1. axay=ax+y
2. ax/ay=ax-y
3. (ax) y=ax.y
4. (a b)x=axbx
5. (a/b)x=ax/bx
6. a-x=1/ax
Relação de Euler
Se i é a unidade imaginária e x é um número real, então vale a relação:
eix = exp(ix) = cos(x) + i sen(x)
Algumas Aplicações
Funções exponenciais desempenham papéis fundamentais na Matemática e nas ciências envolvidas com ela,
como: Física, Química, Engenharia, Astronomia, Economia, Biologia, Psicologia e outras. Vamos apresentar
alguns exemplos com aplicações destas funções.
Lei do resfriamento dos corpos: Um indivíduo foi encontrado morto em uma sala com temperatura
ambiente constante. O legista tomou a temperatura do corpo às 21:00 h e constatou que a mesma era de 32
graus Celsius. Uma hora depois voltou ao local e tomou novamente a temperatura do corpo e constatou que

a mesma estava a 30 graus Celsius. Aproximadamente a que horas morreu o indivíduo, sabendo-se que a
temperatura média de um corpo humano normal é de 37 graus Celsius?
Partindo de estudos matemáticos pode-se construir uma função exponencial decrescente que passa pelos
pontos (21,32) e (22,30) onde abscissas representam o tempo e as ordenadas a temperatura do corpo.
A curva que descreve este fenômeno é uma função exponencial da forma:
f(t) = C eA t
então obtemos que:
A = Ln(30)-Ln(32)
C = 32/ (30/32)21
A função exponencial que rege este fenômeno de resfriamento deste corpo é dada por:
f(t) = 124,09468 e-0,0645385t
e quando f(t) = 37 temos que:
t = 18,7504... = 18 horas + 45 minutos
que pode ser observado através do gráfico.
Observação: Neste exemplo, usamos a construção de um gráfico e as propriedades operatórias das funções
exponenciais e logarítmicas.
Curvas de aprendizagem: Devido ao seu uso por psicólogos e educadores na descrição do processo de
aprendizagem, as curvas exponenciais realizam um papel importante.
A curva básica para este tipo de estudo é da forma:
f(x) = c - a e-k.x
onde c, a e k são constantes positivas. Considerando o caso especial em que c=a temos uma das equações
básicas para descrever a relação entre a consolidação da aprendizagem y=f(x) e o número de reforços x.
A função:
f(x) = c - a e-k.x
cresce rapidamente no começo, nivela-se e então aproxima-se de sua assíntota y=c.
Estas curvas também são estudadas em Economia, na representação de várias funções de custo e produção.
Crescimento populacional: Em 1798, Thomas Malthus, no trabalho "An Essay on the Principle of
Population" formulou um modelo para descrever a população presente em um ambiente em função do

tempo. Considerou N=N(t) o número de indivíduos em certa população no instante t. Tomou as hipóteses
que os nascimentos e mortes naquele ambiente eram proporcionais à população presente e a variação do
tempo conhecida entre os dois períodos. Chegou à seguinte equação para descrever a população presente
em um instante t:
N(t)=No ert
onde No é a população presente no instante inicial t=0 e r é uma constante que varia com a espécie de
população.
O gráfico correto desta função depende dos valores de No e de r. Mas sendo uma função exponencial, a
forma do gráfico será semelhante ao da função y=Kex.
Este modelo supõe que o meio ambiente tenha pouca ou nenhuma influência sobre a população.
Desse modo, ele é mais um indicador do potencial de sobrevivência e de crescimento de cada espécie de
população do que um modelo que mostre o que realmente ocorre.
Consideremos por exemplo uma população de bactérias em um certo ambiente. De acordo com esta
equação se esta população duplicar a cada 20 minutos, dentro de dois dias, estaria formando uma camada
em volta da terra de 30 cm de espessura. Assim, enquanto os efeitos do meio ambiente são nulos, a
população obedece ao modelo N=Noert. Na realidade, se N=N(t) aumenta, o meio ambiente oferece
resistência ao seu crescimento e tende a mantê-lo sobre controle. Exemplos destes fatores são, a quantidade
disponível de alimentos, acidentes, guerras, epidemias,...
Como aplicação numérica, consideremos uma colônia de bactérias se reproduzindo normalmente. Se num
certo instante havia 200 bactérias na colônia, passadas 12 horas havia 600 bactérias. Quantas bactérias
haverá na colônia após 36 horas da última contagem?
No instante inicial havia 200 bactérias, então No=200, após 12 horas havia 600 bactérias, então
N(12)=600=200 er12
logo
e12r=600/200=3
assim
ln(e12r)=ln(3)
Como Ln e exp são funções inversas uma da outra, segue que 12r=ln(3), assim:
r=ln(3)/12=0,0915510
Finalmente:
N(48) = 200 e48.(0,0915510) = 16200 bactérias
Então, após 36 horas da útima contagem ou seja, 48 horas do início da contagem, haverá 16200 bactérias.
Desintegração radioativa: Os fundamentos do estudo da radioatividade ocorrerram no início do século por
Rutherford e outros. Alguns átomos são naturalmente instáveis, de tal modo que após algum tempo, sem
qualquer influência externa sofrem transições para um átomo de um novo elemento químico e durante esta
transição eles emitem radiações. Rutherford formulou um modelo para descrever o modo no qual a

radioatividade decai. Se N=N(t) representa o número de átomos da substância radioativa no instante t, No o
número de átomos no instante t=0 e k é uma constante positiva chamada de constante de decaimento,
então:
N(t) = No e-k.t
esta constante de decaimento k, tem valores diferentes para substâncias diferentes, constantes que são
obtidas experimentalmente.
Na prática usamos uma outra constante T, denominada meia-vida do elemento químico, que é o tempo
necessário para que a quantidade de átomos da substância decaia pela metade.
Se N=No/2 para t=T, temos
No/2 = No e-k.T
assim
T=Ln(2)/k
Na tabela, apresentamos indicadores de meia-vida de alguns elementos químicos:
SubstânciaSubstânciaSubstânciaSubstância Meia-vida TMeia-vida TMeia-vida TMeia-vida T
Xenônio 133Xenônio 133Xenônio 133Xenônio 133 5 dias5 dias5 dias5 dias
Bário 140Bário 140Bário 140Bário 140 13 dias13 dias13 dias13 dias
Chumbo 210Chumbo 210Chumbo 210Chumbo 210 22 anos22 anos22 anos22 anos
Estrôncio 90Estrôncio 90Estrôncio 90Estrôncio 90 25 anos25 anos25 anos25 anos
Carbono 14Carbono 14Carbono 14Carbono 14 5.568 anos5.568 anos5.568 anos5.568 anos
PlutônioPlutônioPlutônioPlutônio 23.103 anos23.103 anos23.103 anos23.103 anos
Urânio 238Urânio 238Urânio 238Urânio 238 4.500.000.000 anos4.500.000.000 anos4.500.000.000 anos4.500.000.000 anos
Para o Carbono 14, a constante de decaimento é:
k = Ln(2)/T = Ln(2)/5568 = 12,3386 por ano
Equações logaritmicas são quaisquer equações que tenham a incógnita (normalmente é x) dentro de um
símbolo log.
Para resolver este tipo de equação não existe um mecanismo geral, algo que dê pra dizer, aplique isso e você
acertará.
Uma regra que deve sempre ser seguida ao terminar a resolução de uma equação logaritmica, é a seguinte:
Todas as soluções encontradas devem ser TESTADAS na equação ORIGINAL, afim de verificar as
condições de existência.
As soluções que não satisfizerem as condições de existência, devem ser DESCARTADAS!
Portanto, para aprendermos a resolver equações logaritmicas, vamos dar uma olhada em algumas questões
chave de vestibulares passados.

01) O conjunto solução da equação logaritmica é:
(A) {-1; 2}
(B) {-2; 1}
(C) {-2}
(D) {1}
(E) { }
Começamos aplicando apenas a equivalência fundamental:
Agora é só aplicar a fórmula de Bhaskara.
Chegando no valor de x devemos TESTAR AS SOLUÇÕES, como dito na única regra de resolução de
equações logaritmicas.
Verificação, para : , OK
para : , OK
Portanto, as duas respostas são válidas. E a alternativa correta é a letra "B"
2) O número real x que satisfaz a equação é:
(A)
(B)
(C)
(D)
(E)
Aplicamos a equivalência fundamental:
Agora caímos em uma equação exponencial do tipo II. Efetuando a troca de variáveis , temos:
Aplicamos Bhaskara e chegamos em:
Agora voltamos para x utilizando novamente a troca de variáveis feita inicialmente :
Absurdo!

Aplicamos a equivalência fundamental,
Agora devemos testar esta solução na equação original do enunciado. Substituindo este valor de x na
equação:
Aplicamos a 4° conseqüência da definição do logaritmo:
Aplicamos a 3° propriedade operatória
, OK. É válida!
Resposta correta, letra "E".
3) A equação tem duas raízes reais. O produto dessas raízes é:
(A)
(B)
(C)
(D)
(E)
Esta equação já envolve um truquezinho, igual às equações exponenciais do tipo II.
Começamos vendo que o 9 na equação pode virar 3².
E aplicamos a 3° propriedade operatória:
O pulo do gato vem agora. Devemos ver que os dois logaritmos envolvidos na equação acima são um o
inverso do outro (1° consequência da mudança de base).
Agora devemos mudar a variável. Efetuamos a troca :
Podemos multiplicar ambos os lados por y, ou efetuar MMC, tanto faz. Chegamos em:

Aplicamos Bhaskara e chegamos em . Estes são os valores de y, o exercício quer os
valores de x. Portanto, utilizamos a troca inicial novamente:
para y=2:
para y=-1:
O produto destes dois valores (como pedido no enunciado) é . Resposta, letra "E".
4) (UFRGS) A solução da equação está no intervalo:
(A) [-2; -1]
(B) (-1; 0]
(C) (0; 1]
(D) (1; 2]
(E) (2; 3]
Esta equação devemos apenas trazer todos os logs para o mesmo lado da igualdade e aplicar as
propriedades operatórias:
Aplicamos a 2° propriedade operatória dos logaritmos:
Aplicamos a equivalência fundamental:
Agora testamos na equação original (do enunciado) para ver as condições de existência. Psara isso,
substituímos o valor de x encontrado na equação do enunciado:
Neste momento não precisamos continuar, só o que devemos saber é que, ao substituir o valor de x, não
encontramos nenhuma falha nas condições de existência dos logaritmos envolvidos. Portanto, a resposta
é mesmo
Este valor encontra-se entre 0 e 1. Resposta correta, letra "C".
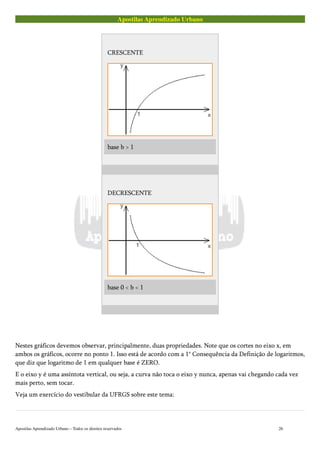
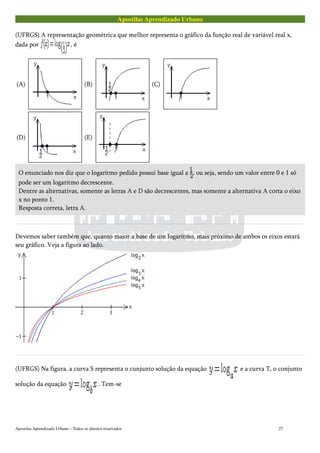
A representação gráfica da função logarítmica deve ser gravada por todos.
Várias questões de vestibular exigem este conhecimento.
A representação gráfica de um logaritmo pode ser de duas formas. Veja os gráficos abaixo mostrando as duas
formas para a função :

CRESCENTE
base b > 1
DECRESCENTE
base 0 < b < 1
Nestes gráficos devemos observar, principalmente, duas propriedades. Note que os cortes no eixo x, em
ambos os gráficos, ocorre no ponto 1. Isso está de acordo com a 1° Consequência da Definição de logaritmos,
que diz que logaritmo de 1 em qualquer base é ZERO.
E o eixo y é uma assíntota vertical, ou seja, a curva não toca o eixo y nunca, apenas vai chegando cada vez
mais perto, sem tocar.
Veja um exercício do vestibular da UFRGS sobre este tema:

(UFRGS) A representação geométrica que melhor representa o gráfico da função real de variável real x,
dada por , é
(A) (B) (C)
(D) (E)
O enunciado nos diz que o logaritmo pedido possui base igual a , ou seja, sendo um valor entre 0 e 1 só
pode ser um logaritmo decrescente.
Dentre as alternativas, somente as letras A e D são decrescentes, mas somente a alternativa A corta o eixo
x no ponto 1.
Resposta correta, letra A.
Devemos saber também que, quanto maior a base de um logaritmo, mais próximo de ambos os eixos estará
seu gráfico. Veja a figura ao lado.
(UFRGS) Na figura, a curva S representa o cunjunto solução da equação e a curva T, o conjunto
solução da equação . Tem-se

(A) a < b < 1
(B) 1 < b < a
(C) 1 < a < b
(D) b < a < 1
(E) b < 1 < a
Os dois gráficos representam logaritmos crescentes, ou seja, ambas as bases são maiores do que 1. Ficamos
então entre as alternativas B e C.
Devemos então saber qual a relação entre a e b. Como a curva S está mais próxima dos eixos x e y do que
a curva T, então sua base é maior (a > b).
Portanto, resposta correta, letra B.
Se, ao invés de termos uma igualdade entre dois logaritmos, tivermos um sinal de desigualdade (<, >, ≥, ≤)
devemos nos atentar a algumas propriedades.
Podemos efetuar todas as operações que fazemos com igualdades.
Em qualquer inequação, quando multiplicamos ou dividimos ambos os lados por um número negativo,
devemos inverter a desigualdade. Por exemplo, a inequação:
1 - x < 0 Podemos passar o 1 para o outro lado:
-x < -1
Agora, devemos multiplicar a inequação por (-1). Com isso, invertemos a
desigualdade
x > 1 E com isso, chegamos ao intervalo da resposta.
Essa regra é para todas inequações.
Para inequações envolvendo logaritmos seguimos alguns passos:
1° Passo
Aplicamos as condições de existência em todos os logaritmos que possuírem a incógnita em
alguma de suas partes.
Guardamos a interesecção destes intervalos encontrados.
2° Passo
Aplicamos as propriedades dos logaritmos a fim de tentar deixar apenas um logaritmo de cada
lado da desigualdade. Ambos com a mesma base.
3° Passo
"Cortamos" os logs dos dois lados, atentando-se para o fato de que se:
base > 1
Mantém-se a
desigualdade
0 < base < 1 Inverte-se a desigualdade
E guardamos também o intervalo encontrado.
4° Passo Computar a intersecção dos intervalos encontrados nos passos 1 e 3.

Veja o exemplo abaixo:
(CAJU) Qual o intervalo solução da inequação:
1° Passo - Pegamos um por dos logaritmandos que possuam "x", e aplicamos as condições de
existência:
Equações Trigonométricas
INTRODUÇÃO
Quando encontramos função trigonométrica da incógnita ou função trigonométrica de alguma função
da incógnita em pelo menos um dos membros de uma equação, dizemos que esta equação é trigonométrica.
Exemplos:
1) sen x + cos x = e sen 2x = cos2 x são equações trigonométricas.
2) x + ( tg 30º) . x2 e x + sen 60º = não são equações trigonométricas.
Dizemos que r é uma raiz ou solução da equação trigonométrica f(x) = g(x) se r for elemento do
domínio de f e g e se f(r) = g(r) for verdadeira.
Na equação sen x - sen =0, por exemplo, os números são algumas de suas raízes e os
números não o são.
O conjunto S de todas as raízes da equação é o seu conjunto solução ou conjunto verdade.
Quase todas as equações trigonométricas, quando convenientemente tratadas e transformadas, podem
ser reduzidas a pelo menos uma das três equações seguintes:
sen x = sen a cos x = cos a tg x = tg a
Estas são as equações trigonométricas elementares ou equações trigonométricas fundamentais.

RESOLUÇÃO DA 1ª EQUAÇÃO FUNDAMENTAL
Ela baseia-se no fato de que, se dois arcos têm o mesmo seno, então eles são côngruos ou suplementares.
Logo, podemos escrever que:
sen x = sen a
O conjunto solução dessa equação será, portanto:
cos x = cos a x = a +
RESOLUÇÃO DA 3ª EQUAÇÃO FUNDAMENTAL
Ela baseia-se no fato de que, se dois arcos têm a mesma tangente, então eles são côngruos ou têm
suas extremidades simétricas em relação ao centro do ciclo trigonométrico.

Função seno
Definição
Chamamos de função seno a função f: R® R que a cada número real x, associa o seno desse número: f: R®
R, f(x) = sen x
O domínio dessa função é R e a imagem é Im [ -1,1] ; visto que, na circunferência trigonométrica o raio é
unitário e, pela definição do seno, –1 £ sen x £ 1, ou seja:
Domínio de f(x) = sen x; D(sen x) = R.
Imagem de f(x) = sen x; Im(sen x) = [ -1,1] .
 Sinal da Função:
Como seno x é a ordenada do ponto-extremidade do arco:
 f(x) = sen x é positiva no 1° e 2° quadrantes (ordenada positiva)
• f(x) = sen x é negativa no 3° e 4° quadrantes (ordenada negativa)
Função cosseno
Definição
Chamamos de função cosseno a função f: R® R que a cada número real x , associa o cosseno desse
número: f: R® R, f(x) = cos x.

O domínio dessa função é R e a imagem é Im [ -1,1] ; visto que, na circunferência trigonométrica o raio é
unitário e, pela definição do cosseno, –1 £ cos x £ 1, ou seja:
Domínio de f(x) = cos x; D(cos x) = R.
Imagem de f(x) = cos x; Im(cos x) = [ -1,1] .
Como cosseno x é a abscissa do ponto-extremidade do arco:
 f(x) = cos x é positiva no 1° e 2° quadrantes (abscissa positiva)
• f(x) = cos x é negativa no 3° e 4° quadrantes (abscissa negativa)
Função tangente
Definição
Chamamos de função tangente a função f: E® R que a cada número xÎ E, com E = í xÎ R/ x ¹ ½ p + kp , kÎ
Zý associa a tangente desse número: f: E® R, f(x) = tg x.
O domínio dessa função é E e a imagem é R; visto que no 1° e 3° quadrantes, a função tg x varia de 0(zero)
até ¥ (infinito) e 2° e 4° quadrantes varia de -¥ (menos infinito) até 0(zero)
Domínio de f(x) = tg x; D(tg x) = E = í xÎ R/ x ¹ ½ p + kp , kÎ Zý .
Imagem de f(x) = tg x; Im(tg x) = R.
Como tangente x é a ordenada do ponto T interseção da reta que passa pelo centro de uma circunferência
trigonométrica e o ponto-extremidade do arco, com o eixo das tangentes então:
 f(x) = tg x é positiva no 1° e 3° quadrantes (produto da ordenada pela abscissa positiva)
 f(x) = tg x é negativa no 2° e 4° quadrantes (produto da ordenada pela abscissa negativa)
Função secante
Definição
Denomina-se função secante a função f(x) = 1/cos x, definida para todo xÎ R diferente de ½p + kp , onde
kÎ Z.
 Sinal da função
Como a função secante é a inversa da função cosseno, então os sinais da função secante são os mesmos da
função cosseno.
Função cossecante
Definição

Denomina-se função cossecante a função f(x) = 1/sen x, definida para todo xÎ R diferente de kp , onde kÎ
Z.
Como a função cossecante é a inversa da função seno, então os sinais da função cossecante são os mesmos
da função seno.
Função cotangente
Definição
Denomina-se função cossecante a função f(x) = 1/sen x, definida para todo xÎ R diferente de kp , onde kÎ Z.
Como a função cossecante é a inversa da função seno, então os sinais da função cossecante são os mesmos
da função seno.
Anexos
A função seno
Observe que esse gráfico é razoável.
Pois:
 Quando , 1º quadrante, o valor de sen x cresce de 0 a 1.

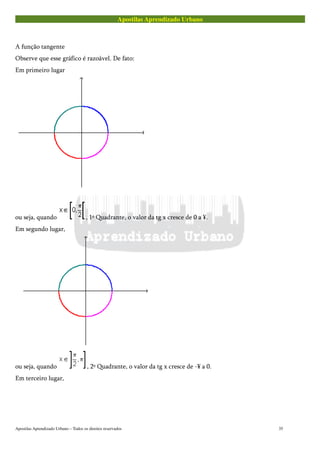
 Quando , 2º quadrante, o valor de sen x decresce de 1 a 0.
 Quando , 3º quadrante, o valor de sen x decresce de 0 a -1.
 Quando , 4º quadrante, o valor de sen x cresce de -1 a 0.]
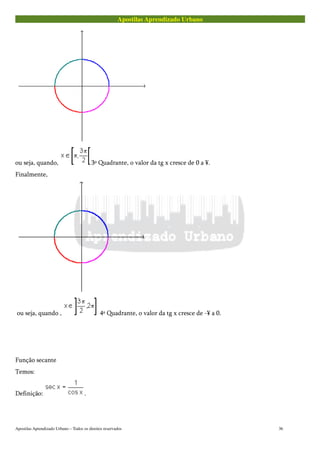
A função cosseno
Observe que esse gráfico é razoável.
Pois:
 Quando , 1º quadrante, o valor do cos x decresce de 1 a 0.
 Quando , 2º quadrante, o valor do cos x decresce de 0 a -1.
 Quando , 3º quadrante, o valor do cos x cresce de -1 a 0.
 Quando , 4º quadrante, o valor do cos x cresce de 0 a 1.

A função tangente
Observe que esse gráfico é razoável. De fato:
Em primeiro lugar
ou seja, quando , 1º Quadrante, o valor da tg x cresce de 0 a ¥.
Em segundo lugar,
ou seja, quando , 2º Quadrante, o valor da tg x cresce de -¥ a 0.
Em terceiro lugar,

ou seja, quando, 3º Quadrante, o valor da tg x cresce de 0 a ¥.
Finalmente,
ou seja, quando , 4º Quadrante, o valor da tg x cresce de -¥ a 0.
Função secante
Temos:
Definição: .

Logo, o domínio da função secante é .
Também, a partir da circunferência trigonométrica, já sabemos que, na figura abaixo, para cada
, sec x é a medida algébrica do segmento OS ou do segmento OT.
Da figura, observamos também que, para todo , , onde k é um número
inteiro qualquer. Assim a função sec é periódica, de período 2p.
A fim de esboçar o gráfico de y=sec x, façamos a análise de como é a variação de y conforme x varia:
 e, nesse intervalo, a função é estritamente crescente, ou seja, conforme x
aumenta, y aumenta;
 e, nesse intervalo, a função é estritamente crescente, ou seja, conforme x
aumenta, y aumenta;
 e, nesse intervalo, a função é estritamente decrescente, ou seja, conforme
x aumenta, y diminui;
 e, nesse intervalo, a função é estritamente decrescente, ou seja, conforme x
aumenta, y diminui.
Observemos que as retas verticais de equação , para k inteiro, não nulo, são assíntotas ao gráfico da
função.

A função y=sec x tem como imagem o intervalo . Ela é uma função não limitada e
periódica, de período 2p
função cossecante
Temos:
Definição: .
Logo, o domínio da função cossecante é
Também, a partir da circunferência trigonométrica, já sabemos que, na figura abaixo, para cada
, cossec x é a medida algébrica do segmento OU ou do segmento OC.

Da figura, observamos também que, qualquer que seja , ,
onde k é um número inteiro qualquer. Assim a função cos sec é periódica, de período 2p.
A fim de esboçar o gráfico de y=cossec x, façamos a análise de como é a variação de y conforme x varia:
 e, nesse intervalo, a função é estritamente decrescente, ou seja, conforme x
aumenta, y diminui;
• e, nesse intervalo, a função é estritamente decrescente, ou seja, conforme x
aumenta, y diminui;
Observemos que as retas verticais de equação , para k inteiro, não nulo, são assíntotas ao gráfico da
função.
A função y=cotg x tem como imagem o intervalo . Ela é uma função não limitada e periódica.
Análise combinatória, progressão aritmética, progressão geométrica e probabilidade básica
Análise Combinatória é um conjunto de procedimentos que possibilita a construção de grupos diferentes
formados por um número finito de elementos de um conjunto sob certas circunstâncias.
Na maior parte das vezes, tomaremos conjuntos Z com m elementos e os grupos formados com elementos
de Z terão p elementos, isto é, p será a taxa do agrupamento, com p<m.
Arranjos, Permutações ou Combinações, são os três tipos principais de agrupamentos, sendo que eles podem
ser simples, com repetição ou circulares. Apresentaremos alguns detalhes de tais agrupamentos.
Observação: É comum encontrarmos na literatura termos como: arranjar, combinar ou permutar, mas todo
o cuidado é pouco com os mesmos, que às vezes são utilizados em concursos em uma forma dúbia!

Arranjos
São agrupamentos formados com p elementos, (p<m) de forma que os p elementos sejam distintos entre sí
pela ordem ou pela espécie. Os arranjos podem ser simples ou com repetição.
Arranjo simples: Não ocorre a repetição de qualquer elemento em cada grupo de p elementos.
Fórmula: As(m,p) = m!/(m-p)!
Cálculo para o exemplo: As(4,2) = 4!/2!=24/2=12.
Exemplo: Seja Z={A,B,C,D}, m=4 e p=2. Os arranjos simples desses 4 elementos tomados 2 a 2 são 12 grupos
que não podem ter a repetição de qualquer elemento mas que podem aparecer na ordem trocada. Todos os
agrupamentos estão no conjunto:
As={AB,AC,AD,BA,BC,BD,CA,CB,CD,DA,DB,DC}
Arranjo com repetição: Todos os elementos podem aparecer repetidos em cada grupo de p elementos.
Fórmula: Ar(m,p) = mp.
Cálculo para o exemplo: Ar(4,2) = 42=16.
Exemplo: Seja C={A,B,C,D}, m=4 e p=2. Os arranjos com repetição desses 4 elementos tomados 2 a 2 são 16
grupos que onde aparecem elementos repetidos em cada grupo. Todos os agrupamentos estão no conjunto:
Ar={AA,AB,AC,AD,BA,BB,BC,BD,CA,CB,CC,CD,DA,DB,DC,DD}
Arranjo condicional: Todos os elementos aparecem em cada grupo de p elementos, mas existe uma condição
que deve ser satisfeita acerca de alguns elementos.
Fórmula: N=A(m1,p1).A(m-m1,p-p1)
Cálculo para o exemplo: N=A(3,2).A(7-3,4-2)=A(3,2).A(4,2)=6×12=72.
Exemplo: Quantos arranjos com 4 elementos do conjunto {A,B,C,D,E,F,G}, começam com duas letras
escolhidas no subconjunto {A,B,C}?
Aqui temos um total de m=7 letras, a taxa é p=4, o subconjunto escolhido tem m1=3 elementos e a taxa que
este subconjunto será formado é p1=2. Com as letras A,B e C, tomadas 2 a 2, temos 6 grupos que estão no
conjunto:
PABC = {AB,BA,AC,CA,BC,CB}
Com as letras D,E,F e G tomadas 2 a 2, temos 12 grupos que estão no conjunto:
PDEFG = {DE,DF,DG,ED,EF,EG,FD,FE,FG,GD,GE,GF}
Usando a regra do produto, teremos 72 possibilidades obtidas pela junção de um elemento do conjunto
PABC com um elemento do conjunto PDEFG. Um típico arranjo para esta situação é CAFG.
Permutações
Quando formamos agrupamentos com m elementos, de forma que os m elementos sejam distintos entre sí
pela ordem. As permutações podem ser simples, com repetição ou circulares.
Permutação simples: São agrupamentos com todos os m elementos distintos.
Fórmula: Ps(m) = m!.

Cálculo para o exemplo: Ps(3) = 3!=6.
Exemplo: Seja C={A,B,C} e m=3. As permutações simples desses 3 elementos são 6 agrupamentos que não
podem ter a repetição de qualquer elemento em cada grupo mas podem aparecer na ordem trocada. Todos
os agrupamentos estão no conjunto:
Ps={ABC,ACB,BAC,BCA,CAB,CBA}
Permutação com repetição: Dentre os m elementos do conjunto C={x1,x2,x3,...,xn}, faremos a suposição que
existem m1 iguais a x1, m2 iguais a x2, m3 iguais a x3, ... , mn iguais a xn, de modo que m1+m2+m3+...
+mn=m.
Fórmula: Se m=m1+m2+m3+...+mn, então
Pr(m)=C(m,m1).C(m-m1,m2).C(m-m1-m2,m3) ... C(mn,mn)
Anagrama: Um anagrama é uma (outra) palavra construída com as mesmas letras da palavra original
trocadas de posição.
Cálculo para o exemplo: m1=4, m2=2, m3=1, m4=1 e m=6, logo: Pr(6)=C(6,4).C(6-4,2).C(6-4-
1,1)=C(6,4).C(2,2).C(1,1)=15.
Exemplo: Quantos anagramas podemos formar com as 6 letras da palavra ARARAT. A letra A ocorre 3
vezes, a letra R ocorre 2 vezes e a letra T ocorre 1 vez. As permutações com repetição desses 3 elementos do
conjunto C={A,R,T} em agrupamentos de 6 elementos são 15 grupos que contêm a repetição de todos os
elementos de C aparecendo também na ordem trocada. Todos os agrupamentos estão no conjunto:
Pr={AAARRT,AAATRR,AAARTR,AARRTA,AARTTA,
AATRRA,AARRTA,ARAART,ARARAT,ARARTA,
ARAATR,ARAART,ARAATR,ATAARA,ATARAR}
Permutação circular: Situação que ocorre quando temos grupos com m elementos distintos formando uma
circunferência de círculo.
Fórmula: Pc(m)=(m-1)!
Cálculo para o exemplo: P(4)=3!=6
Exemplo: Seja um conjunto com 4 pessoas K={A,B,C,D}. De quantos modos distintos estas pessoas poderão
sentar-se junto a uma mesa circular (pode ser retangular) para realizar o jantar sem que haja repetição das
posições?
Se considerássemos todas as permutações simples possíveis com estas 4 pessoas, teriamos 24 grupos,
apresentados no conjunto:
Pc={ABCD,ABDC,ACBD,ACDB,ADBC,ADCB,BACD,BADC,
BCAD,BCDA,BDAC,BDCA,CABD,CADB,CBAD,CBDA,
CDAB,CDBA, DABC,DACB,DBAC,DBCA,DCAB,DCBA}
Acontece que junto a uma mesa "circular" temos que:
ABCD=BCDA=CDAB=DABC
ABDC=BDCA=DCAB=CABD
ACBD=CBDA=BDAC=DACB
ACDB=CDBA=DBAC=BACD
ADBC=DBCA=BCAD=CADB

ADCB=DCBA=CBAD=BADC
Existem somente 6 grupos distintos, dados por:
Pc={ABCD,ABDC,ACBD,ACDB,ADBC,ADCB}
Combinações
Quando formamos agrupamentos com p elementos, (p<m) de forma que os p elementos sejam distintos
entre sí apenas pela espécie.
Combinação simples: Não ocorre a repetição de qualquer elemento em cada grupo de p elementos.
Fórmula: C(m,p) = m!/[(m-p)! p!]
Cálculo para o exemplo: C(4,2)=4!/[2!2!]=24/4=6
Exemplo: Seja C={A,B,C,D}, m=4 e p=2. As combinações simples desses 4 elementos tomados 2 a 2 são 6
grupos que não podem ter a repetição de qualquer elemento nem podem aparecer na ordem trocada. Todos
os agrupamentos estão no conjunto:
Cs={AB,AC,AD,BC,BD,CD}
Combinação com repetição: Todos os elementos podem aparecer repetidos em cada grupo até p vezes.
Fórmula: Cr(m,p)=C(m+p-1,p)
Cálculo para o exemplo: Cr(4,2)=C(4+2-1,2)=C(5,2)=5!/[2!3!]=10
Exemplo: Seja C={A,B,C,D}, m=4 e p=2. As combinações com repetição desses 4 elementos tomados 2 a 2
são 10 grupos que têm todas as repetições possíveis de elementos em grupos de 2 elementos não podendo
aparecer o mesmo grupo com a ordem trocada. De um modo geral neste caso, todos os agrupamentos com 2
elementos formam um conjunto com 16 elementos:
Cr={AA,AB,AC,AD,BA,BB,BC,BD,CA,CB,CC,CD,DA,DB,DC,DD}
mas para obter as combinações com repetição, deveremos excluir deste conjunto os 6 grupos que já
apareceram antes, pois AB=BA, AC=CA, AD=DA, BC=CB, BD=DB e CD=DC, assim as combinações com
repetição dos elementos de C tomados 2 a 2, são:
Cr={AA,AB,AC,AD,BB,BC,BD,CC,CD,DD}
Regras gerais sobre a Análise Combinatória
Problemas de Análise Combinatória normalmente são muito difíceis mas eles podem ser resolvidos através
de duas regras básicas: a regra da soma e a regra do produto.
Regra da soma: A regra da soma nos diz que se um elemento pode ser escolhido de m formas e um outro
elemento pode ser escolhido de n formas, então a escolha de um ou outro elemento se realizará de m+n
formas, desde que tais escolhas sejam independentes, isto é, nenhuma das escolhas de um elemento pode
coincidir com uma escolha do outro.
Regra do Produto: A regra do produto diz que se um elemento H pode ser escolhido de m formas diferentes
e se depois de cada uma dessas escolhas, um outro elemento M pode ser escolhido de n formas diferentes, a
escolha do par (H,M) nesta ordem poderá ser realizada de m.n formas.

Exemplo: Consideremos duas retas paralelas ou concorrentes sem que os pontos sob análise estejam em
ambas, sendo que a primeira r contem m pontos distintos marcados por r1, r2, r3, ..., rm e a segunda s
contem n outros pontos distintos marcados por s1, s2, s3, ..., sn. De quantas maneiras podemos traçar
segmentos de retas com uma extremidade numa reta e a outra extremidade na outra reta?
É fácil ver isto ligando r1 a todos os pontos de s e assim teremos n segmentos, depois ligando r2 a todos os
pontos de s e assim teremos n segmentos, e continuamos até o último ponto para obter também n
segmentos. Como existem m pontos em r e n pontos em s, teremos m.n segmentos possíveis.
Número de Arranjos simples
Seja C um conjunto com m elementos. De quantas maneiras diferentes poderemos escolher p elementos
(p<m) deste conjunto? Cada uma dessas escolhas será chamada um arranjo de m elementos tomados p a p.
Construiremos uma sequência com os m elementos de C.
c1, c2, c3, c4, c5, ..., cm-2, cm-1, cm
Cada vez que um elemento for retirado, indicaremos esta operação com a mudança da cor do elemento para
a cor vermelha.
Para escolher o primeiro elemento do conjunto C que possui m elementos, temos m possibilidades. Vamos
supor que a escolha tenha caído sobre o m-ésimo elemento de C.
c1, c2, c3, c4, c5, ..., cm-2, cm-1, cm
Para escolher o segundo elemento, devemos observar o que sobrou no conjunto e constatamos que agora
existem apenas m-1 elementos. Suponhamos que tenha sido retirado o último elemento dentre os que
sobraram no conjunto C. O elemento retirado na segunda fase é o (m-1)-ésimo.
c1, c2, c3, c4, c5, ..., cm-2, cm-1, cm
Após a segunda retirada, sobraram m-2 possibilidades para a próxima retirada. Do que sobrou, se retirarmos
o terceiro elemento como sendo o de ordem (m-2), teremos algo que pode ser visualizado como:
c1, c2, c3, c4, c5, ..., cm-2, cm-1, cm
Se continuarmos o processo de retirada, cada vez teremos 1 elemento a menos do que na fase anterior. Para
retirar o p-ésimo elemento, restarão m-p+1 possibilidades de escolha.
Para saber o número total de arranjos possíveis de m elementos tomados p a p, basta multiplicar os números
que aparecem na segunda coluna da tabela abaixo:
RetiradaRetiradaRetiradaRetirada Número de possibilidadesNúmero de possibilidadesNúmero de possibilidadesNúmero de possibilidades
1111 mmmm
2222 m-1m-1m-1m-1
3333 m-2m-2m-2m-2
............ ............
pppp m-p+1m-p+1m-p+1m-p+1
No.de arranjosNo.de arranjosNo.de arranjosNo.de arranjos m(m-1)(m-2)...(m-p+1)m(m-1)(m-2)...(m-p+1)m(m-1)(m-2)...(m-p+1)m(m-1)(m-2)...(m-p+1)

Denotaremos o número de arranjos de m elementos tomados p a p, por A(m,p) e a expressão para seu
cálculo será dada por:
A(m,p) = m(m-1)(m-2)...(m-p+1)
Exemplo: Consideremos as 5 vogais de nosso alfabeto. Quais e quantas são as possibilidades de dispor estas 5
vogais em grupos de 2 elementos diferentes? O conjunto solução é:
{AE,AI,AO,AU,EA,EI,EO,EU,IA,IE,
IO,IU,OA,OE,OI,OU,UA,UE,UI,UO}
A solução numérica é A(5,2)=5×4=20.
Exemplo: Consideremos as 5 vogais de nosso alfabeto. Quais e quantas são as possibilidades de dispor estas 5
vogais em grupos de 2 elementos (não necessariamente diferentes)?
Sugestão: Construir uma reta com as 5 vogais e outra reta paralela à anterior com as 5 vogais, usar a regra do
produto para concluir que há 5x5=25 possibilidades.
O conjunto solução é:
{AA,AE,AI,AO,AU,EA,EE,EI,EO,EU,IA,IE,II,
IO,IU,OA,OE,OI,OO,OU,UA,UE,UI,UO,UU}
Exemplo: Quantas placas de carros podem existir no atual sistema brasileiro de trânsito que permite 3 letras
iniciais e 4 algarismos no final?
XYZ-1234
Sugestão: Considere que existem 26 letras em nosso alfabeto que podem ser dispostas 3 a 3 e 10 algarismos
que podem ser dispostos 4 a 4 e em seguida utilize a regra do produto.
Número de Permutações simples
Este é um caso particular de arranjo em que p=m. Para obter o número de permutações com m elementos
distintos de um conjunto C, basta escolher os m elementos em uma determinada ordem. A tabela de
arranjos com todas as linhas até a ordem p=m, permitirá obter o número de permutações de m elementos:
RetiradaRetiradaRetiradaRetirada Número de possibilidadesNúmero de possibilidadesNúmero de possibilidadesNúmero de possibilidades
1111 mmmm
2222 m-1m-1m-1m-1
............ ............
pppp m-p+1m-p+1m-p+1m-p+1
............ ............
m-2m-2m-2m-2 3333
m-1m-1m-1m-1 2222
mmmm 1111
No.de permutaçõesNo.de permutaçõesNo.de permutaçõesNo.de permutações
m(m-1)(m-2)...(m-m(m-1)(m-2)...(m-m(m-1)(m-2)...(m-m(m-1)(m-2)...(m-
p+1)...4.3.2.1p+1)...4.3.2.1p+1)...4.3.2.1p+1)...4.3.2.1
Denotaremos o número de permutações de m elementos, por P(m) e a expressão para seu cálculo será dada

por:
P(m) = m(m-1)(m-2) ... (m-p+1) ... 3 . 2 . 1
Em função da forma como construímos o processo, podemos escrever:
A(m,m) = P(m)
Como o uso de permutações é muito intenso em Matemática e nas ciências em geral, costuma-se simplificar
a permutação de m elementos e escrever simplesmente:
P(m) = m!
Este símbolo de exclamação posto junto ao número m é lido como: fatorial de m, onde m é um número
natural.
Embora zero não seja um número natural no sentido que tenha tido origem nas coisas da natureza, procura-
se dar sentido para a definição de fatorial de m de uma forma mais ampla, incluindo m=0 e para isto
podemos escrever:
0!=1
Em contextos mais avançados, existe a função gama que generaliza o conceito de fatorial de um número
real, excluindo os inteiros negativos e com estas informações pode-se demonstrar que 0!=1.
O fatorial de um número inteiro não negativo pode ser definido de uma forma recursiva através da função
P=P(m) ou com o uso do sinal de exclamação:
(m+1)! = (m+1).m!, 0! = 1
Exemplo: De quantos modos podemos colocar juntos 3 livros A, B e C diferentes em uma estante? O
número de arranjos é P(3)=6 e o conjunto solução é:
P={ABC,ACB,BAC,BCA,CAB,CBA}
Exemplo: Quantos anagramas são possíveis com as letras da palavra AMOR? O número de arranjos é
P(4)=24 e o conjunto solução é:
P={AMOR,AMRO,AROM,ARMO,AORM,AOMR,MARO,MAOR,
MROA,MRAO,MORA,MOAR,OAMR,OARM,ORMA,ORAM,
OMAR,OMRA,RAMO,RAOM,RMOA,RMAO,ROAM,ROMA}
Número de Combinações simples
Seja C um conjunto com m elementos distintos. No estudo de arranjos, já vimos antes que é possível
escolher p elementos de A, mas quando realizamos tais escolhas pode acontecer que duas coleções com p
elementos tenham os mesmos elementos em ordens trocadas. Uma situação típica é a escolha de um casal
(H,M). Quando se fala casal, não tem importância a ordem da posição (H,M) ou (M,H), assim não há a
necessidade de escolher duas vezes as mesmas pessoas para formar o referido casal. Para evitar a repetição
de elementos em grupos com a mesma quantidade p de elementos, introduziremos o conceito de
combinação.
Diremos que uma coleção de p elementos de um conjunto C com m elementos é uma combinação de m
elementos tomados p a p, se as coleções com p elementos não tem os mesmos elementos que já apareceram
em outras coleções com o mesmo número p de elementos.

Aqui temos outra situação particular de arranjo, mas não pode acontecer a repetição do mesmo grupo de
elementos em uma ordem diferente.
Isto significa que dentre todos os A(m,p) arranjos com p elementos, existem p! desses arranjos com os
mesmos elementos, assim, para obter a combinação de m elementos tomados p a p, deveremos dividir o
número A(m,p) por m! para obter apenas o número de arranjos que contem conjuntos distintos, ou seja:
C(m,p) = A(m,p) / p!
Como
A(m,p) = m.(m-1).(m-2)...(m-p+1)
então:
C(m,p) = [ m.(m-1).(m-2). ... .(m-p+1)] / p!
que pode ser reescrito
C(m,p)=[m.(m-1).(m-2)...(m-p+1)]/[(1.2.3.4....(p-1)p]
Multiplicando o numerador e o denominador desta fração por
(m-p)(m-p-1)(m-p-2)...3.2.1
que é o mesmo que multiplicar por (m-p)!, o numerador da fração ficará:
m.(m-1).(m-2).....(m-p+1)(m-p)(m-p-1)...3.2.1 = m!
e o denominador ficará:
p! (m-p)!
Assim, a expressão simplificada para a combinação de m elementos tomados p a p, será uma das seguintes:
Número de arranjos com repetição
Seja C um conjunto com m elementos distintos e considere p elementos escolhidos neste conjunto em uma
ordem determinada. Cada uma de tais escolhas é denominada um arranjo com repetição de m elementos
tomados p a p. Acontece que existem m possibilidades para a colocação de cada elemento, logo, o número
total de arranjos com repetição de m elementos escolhidos p a p é dado por mp. Indicamos isto por:
Arep(m,p) = mp
Número de permutações com repetição
Consideremos 3 bolas vermelhas, 2 bolas azuis e 5 bolas amarelas. Coloque estas bolas em uma ordem
determinada. Iremos obter o número de permutações com repetição dessas bolas. Tomemos 10
compartimentos numerados onde serão colocadas as bolas. Primeiro coloque as 3 bolas vermelhas em 3
compartimentos, o que dá C(10,3) possibilidades. Agora coloque as 2 bolas azuis nos compartimentos
restantes para obter C(10-3,2) possibilidades e finalmente coloque as 5 bolas amarelas. As possibilidades são
C(10-3-2,5).

O número total de possibilidades pode ser calculado como:
Tal metodologia pode ser generalizada.
Número de combinações com repetição
Considere m elementos distintos e ordenados. Escolha p elementos um após o outro e ordene estes
elementos na mesma ordem que os elementos dados. O resultado é chamado uma combinação com
repetição de m elementos tomados p a p. Denotamos o número destas combinações por Crep(m,p). Aqui a
taxa p poderá ser maior do que o número m de elementos.
Seja o conjunto A=(a,b,c,d,e) e p=6. As coleções (a,a,b,d,d,d), (b,b,b,c,d,e) e (c,c,c,c,c,c) são exemplos de
combinações com repetição de 5 elementos escolhidos 6 a 6.
Podemos representar tais combinações por meio de símbolos # e vazios Ø onde cada ponto # é repetido (e
colocado junto) tantas vezes quantas vezes aparece uma escolha do mesmo tipo, enquanto o vazio Ø serve
para separar os objetos em função das suas diferenças
(a,a,b,d,d,d) equivale a ##Ø#ØØ###Ø
(b,b,b,c,d,e) equivale a Ø###Ø#Ø#Ø#
(c,c,c,c,c,c) equivale a ØØ######ØØ
Cada símbolo possui 10 lugares com exatamente 6# e 4Ø. Para cada combinação existe uma
correspondência biunívoca com um símbolo e reciprocamente. Podemos construir um símbolo pondo
exatamente 6 pontos em 10 lugares. Após isto, os espaços vazios são prenchidos com barras. Isto pode ser
feito de C(10,6) modos. Assim:
Crep(5,6) = C(5+6-1,6)
Generalizando isto, podemos mostrar que:
Crep(m,p) = C(m+p-1,p)
Propriedades das combinações
O segundo número, indicado logo acima por p é conhecido como a taxa que define a quantidade de
elementos de cada escolha.
Taxas complementares
C(m,p)=C(m,m-p)
Exemplo: C(12,10) = C(12,2)=66.
Relação do triângulo de Pascal
C(m,p)=C(m-1,p)+C(m-1,p-1)
Exemplo: C(12,10)=C(11,10)+C(11,9)=605

Número Binomial
O número de combinações de m elementos tomados p a p, indicado antes por C(m,p) é chamado
Coeficiente Binomial ou número binomial, denotado na literatura científica como:
Exemplo: C(8,2)=28.
Extensão: Existe uma importante extensão do conceito de número binomial ao conjunto dos números reais
e podemos calcular o número binomial de qualquer número real r que seja diferente de um número inteiro
negativo, tomado a uma taxa inteira p, somente que, neste caso, não podemos mais utilizar a notação de
combinação C(m,p) pois esta somente tem sentido quando m e p são números inteiros não negativos. Como
Pi=3,1415926535..., então:
A função envolvida com este contexto é a função gama. Tais cálculos são úteis em Probabilidade e
Estatística.
Teorema Binomial
Se m é um número natural, para simplificar um pouco as notações, escreveremos mp no lugar de C(m,p).
Então:
(a+b)m = am+m1am-1b+m2am-2b2+m3am-3b3+...+mmbm
Alguns casos particulares com m=2, 3, 4 e 5, são:
(a+b)2 = a2 + 2ab + b2
(a+b)3 = a3 + 3 a2b + 3 ab2 + b3
(a+b)4 = a4 + 4 a3b + 6 a2b2 + 4 ab3 + b4
(a+b)5 = a5 + 5 a4b + 10 a3b2 + 10 a2b3 + 5 ab4 + b5
A demonstração segue pelo Princípio da Indução Matemática.
Iremos considerar a Proposição P(m) de ordem m, dada por:
P(m): (a+b)m=am+m1am-1b+m2am-2b2+m3am-3b3+...+mmbm
P(1) é verdadeira pois (a+b)1 = a + b
Vamos considerar verdadeira a proposição P(k), com k>1:
P(k): (a+b)k=ak+k1ak-1b+k2ak-2b2+k3ak-3b3+...+kkbk
para provar a propriedade P(k+1).
Para que a proposição P(k+1) seja verdadeira, deveremos chegar à conclusão que:
(a+b)k+1=ak+1+(k+1)1akb+(k+1)2ak-1b2+...+(k+1)(k+1)bk+1

(a+b)k+1=(a+b)k+1=(a+b)k+1=(a+b)k+1= (a+b).(a+b)k
==== (a+b).[ak+k1ak-1b+k2ak-2b2+k3ak-3b3+...+kkbk]
====
a.[ak+k1ak-1b+k2ak-2 b2+k3ak-3b3+...+kkbk]
+b.[ak+k1ak-1b+k2ak-2b2+k3ak-3b3+...+kk bk]
====
ak+1+k1akb+k2ak-1b2+k3ak-2b3+...+kkabk
+akb+k1ak-1b2+k2ak-2 b3+k3ak-3b4+...+kkbk+1
====
ak+1+[k1+1]akb+[k2+k1]ak-1b2+[k3+k2]ak-2b3
+[k4+k3] ak-3b4+...+[kk-1+kk-2]a2bk-1+[kk+kk-
1]abk+kkbk+1
====
ak+1+[k1+k0] akb+[k2+k1]ak-1b2+[k3+k2]ak-2b3
+[k4+k3]ak-3b4+...+[kk-1+kk-2]a2bk-1+[kk+kk-
1]abk+kkbk+1
Pelas propriedades das combinações, temos:
k1+k0=C(k,1)+C(k,0)=C(k+1,1)=(k+1)1
k2+k1=C(k,2)+C(k,1)=C(k+1,2)=(k+1)2
k3+k2=C(k,3)+C(k,2)=C(k+1,3)=(k+1)3
k4+k3=C(k,4)+C(k,3)=C(k+1,4)=(k+1)4
... ... ... ...
kk-1+kk-2=C(k,k-1)+C(k,k-2)=C(k+1,k-1)=(k+1)k-1
kk+kk-1=C(k,k)+C(k,k-1)=C(k+1,k)=(k+1)k
E assim podemos escrever:
(a+b)k+1=
ak+1+(k+1)1akb + (k+1)2ak-1b2 + (k+1)3ak-2b3
+(k+1)4ak-3b4 +...+ (k+1)k-1a2bk-1 + (k+1)kabk +
kkbk+1
que é o resultado desejado.
Progressão Aritmética, PAProgressão Aritmética, PAProgressão Aritmética, PAProgressão Aritmética, PA
Chama-se seqüência ou sucessão numérica, a qualquer conjunto ordenado de números reais ou complexos.
Assim, por exemplo, o conjunto ordenado A = ( 3, 5, 7, 9, 11, ... , 35) é uma seqüência cujo primeiro termo é
3, o segundo termo é 5, o terceiro termo é 7 e assim sucessivamente.
Uma seqüência pode ser finita ou infinita.
O exemplo dado acima é de uma seqüência finita.
Já a seqüência P = (0, 2, 4, 6, 8, ... ) é infinita.
Uma seqüência numérica pode ser representada genericamente na forma:
(a1, a2, a3, ... , ak, ... , an, ...) onde a1 é o primeiro termo, a2 é o segundo termo, ... , ak é o k-ésimo termo, ...
, an é o n-ésimo termo. (Neste caso, k < n).

Por exemplo, na seqüência Y = ( 2, 6, 18, 54, 162, 486, ... ) podemos dizer que a3 = 18, a5 = 162, etc.
São de particular interesse, as seqüências cujos termos obedecem a uma lei de formação, ou seja é possível
escrever uma relação matemática entre eles.
Assim, na seqüência Y acima, podemos observar que cada termo a partir do segundo é igual ao anterior
multiplicado por 3.
A lei de formação ou seja a expressão matemática que relaciona entre si os termos da seqüência, é
denominada termo geral.
Considere por exemplo a seqüência S cujo termo geral seja dado por an = 3n + 5, onde n é um número
natural não nulo.
Observe que atribuindo-se valores para n, obteremos o termo an (n - ésimo termo) correspondente.
Assim por exemplo, para n = 20, teremos
an = 3.20 + 5 = 65, e portanto o vigésimo termo dessa seqüência (a20) é igual a 65.
Prosseguindo com esse raciocínio, podemos escrever toda a seqüência S que seria:
S = ( 8, 11, 14, 17, 20, ... ).
Dado o termo geral de uma seqüência, é sempre fácil determiná-la.
Seja por exemplo a seqüência de termo geral an = n2 + 4n + 10, para n inteiro e positivo.
Nestas condições, podemos concluir que a seqüência poderá ser escrita como:
(15, 22, 31, 42, 55, 70, ... ).
Por exemplo:
a6 = 70 porque a6 = 62 + 4.6 + 10 = 36 + 24 + 10 = 70.
2 - Conceito de Progressão Aritmética - PA
Chama-se Progressão Aritmética – PA – à toda seqüência numérica cujos termos a partir do segundo, são
iguais ao anterior somado com um valor constante denominado razão.
Exemplos:
A = ( 1, 5, 9, 13, 17, 21, ... ) razão = 4 (PA crescente)
B = ( 3, 12, 21, 30, 39, 48, ... ) razão = 9 (PA crescente)
C = ( 5, 5, 5, 5, 5, 5, 5, ... ) razão = 0 (PA constante)
D = ( 100, 90, 80, 70, 60, 50, ... ) razão = -10 ( PA decrescente)
3 - Termo Geral de uma PA
Seja a PA genérica (a1, a2, a3, ... , an, ...) de razão r.
De acordo com a definição podemos escrever:
a2 = a1 + 1.r
a3 = a2 + r = (a1 + r) + r = a1 + 2r
a4 = a3 + r = (a1 + 2r) + r = a1 + 3r
.....................................................
Podemos inferir (deduzir) das igualdades acima que: .............. an = a1 + (n – 1) . r
A expressão an = a1 + (n – 1) . r é denominada termo geral da PA.
Nesta fórmula, temos que an é o termo de ordem n (n-ésimo termo) , r é a razão e a1 é o primeiro termo da
Progressão Aritmética – PA.
Exemplos:

Qual o milésimo número ímpar positivo?
Temos a PA: ( 1, 3, 5, 7, 9, ... ) onde o primeiro termo a1= 1, a razão r = 2 e queremos calcular o milésimo
termo a1000. Nestas condições, n = 1000 e poderemos escrever:
a1000 = a1 + (1000 - 1).2 = 1 + 999.2 = 1 + 1998 = 1999.
Portanto, 1999 é o milésimo número ímpar.
Qual o número de termos da PA: ( 100, 98, 96, ... , 22) ?
Temos a1 = 100, r = 98 -100 = - 2 e an = 22 e desejamos calcular n.
Substituindo na fórmula do termo geral, fica: 22 = 100 + (n - 1). (- 2) ;
logo, 22 - 100 = - 2n + 2 e, 22 - 100 - 2 = - 2n de onde conclui-se que - 80 = - 2n ,
de onde vem n = 40.
Portanto, a PA possui 40 termos.
Através de um tratamento simples e conveniente da fórmula do termo geral de uma PA, podemos
generaliza-la da seguinte forma:
Sendo aj o termo de ordem j (j-ésimo termo) da PA e ak o termo de ordem k ( k-ésimo termo) da PA,
poderemos escrever a seguinte fórmula genérica:
aj = ak + (j - k).r
Exemplos:
Se numa PA o quinto termo é 30 e o vigésimo termo é 60, qual a razão?
Temos a5 = 30 e a20 = 60.
Pela fórmula anterior, poderemos escrever:
a20 = a5 + (20 - 5) . r e substituindo fica: 60 = 30 + (20 - 5).r ;
60 - 30 = 15r ; logo, r = 2.
Numa PA de razão 5, o vigésimo termo vale 8. Qual o terceiro termo?
Temos r = 5, a20 = 8.
Logo, o termo procurado será: a3 = a20 + (3 – 20).5
a3 = 8 –17.5 = 8 – 85 = - 77.
4 - Propriedades das Progressões Aritméticas
Numa PA, cada termo (a partir do segundo) é a média aritmética dos termos vizinhos deste.
Exemplo:
PA : ( m, n, r ) ; portanto, n = (m + r) / 2
Assim, se lhe apresentarem um problema de PA do tipo:
Três números estão em PA, ... , a forma mais inteligente de resolver o problema é considerar que a PA é do
tipo:
(x - r, x, x + r), onde r é a razão da PA.
Numa PA, a soma dos termos eqüidistantes dos extremos é constante.
Exemplo:
PA : ( m, n, r, s, t); portanto, m + t = n + s = r + r = 2r
Estas propriedades facilitam sobremaneira a solução de problemas.
5 - Soma dos n primeiros termos de uma PA

Seja a PA ( a1, a2, a3, ..., an-1, an).
A soma dos n primeiros termos Sn = a1 + a2 + a3 + ... + an-1 + an , pode ser deduzida facilmente, da
aplicação da segunda propriedade acima.
Temos:
Sn = a1 + a2 + a3 + ... + an-1 + an
É claro que também poderemos escrever a igualdade acima como:
Sn = an + an-1 + ... + a3 + a2 + a1
Somando membro a membro estas duas igualdades, vem:
2. Sn = (a1 + an) + (a2 + an-1) + ... + (an + a1)
Logo, pela segunda propriedade acima, as n parcelas entre parênteses possuem o mesmo valor ( são iguais à
soma dos termos extremos a1 + an ) , de onde concluímos inevitavelmente que:
2.Sn = (a1 + an).n , onde n é o número de termos da PA.
Daí então, vem finalmente que:
Exemplo:
Calcule a soma dos 200 primeiros números ímpares positivos.
Temos a PA: ( 1, 3, 5, 7, 9, ... )
Precisamos conhecer o valor de a200 .
Mas, a200 = a1 + (200 - 1).r = 1 + 199.2 = 399
Logo, Sn = [(1 + 399). 200] / 2 = 40.000
Portanto, a soma dos duzentos primeiros números ímpares positivos é igual a 40000.
Exercícios resolvidos e propostos:
1 - Qual é o número mínimo de termos que se deve somar na P.A. :( 7/5 , 1 , 3/5 , ... ) , a partir do primeiro
termo, para que a soma seja negativa?
*a) 9
b) 8
c) 7
d ) 6
e) 5
SOLUÇÃO:
Temos: a1 = 7/5 e r = 1 – 7/5 = 5/5 – 7/5 = -2/5, ou seja: r = -2/5.
Poderemos escrever então, para o n-ésimo termo an:
an = a1 + (n – 1).r = 7/5 + (n – 1).(-2/5)
an = 7/5 – 2n/5 + 2/5 = (7/5 + 2/5) –2n/5 = 9/5 –2n/5 = (9 – 2n)/5
A soma dos n primeiros termos, pela fórmula vista anteriormente será então:
Sn = (a1 + an). (n/2) = [(7/5) + (9 – 2n)/5].(n/2) = [(16 – 2n)/5].(n/2)
Sn = (16n – 2n2) / 10
Ora, nós queremos que a soma Sn seja negativa; logo, vem:
(16n – 2n2) / 10 < 0

Como o denominador é positivo, para que a fração acima seja negativa, o numerador deve ser negativo.
Logo, deveremos ter:
16n – 2n2 < 0
Portanto, n(16 – 2n ) < 0
Ora, como n é o número de termos, ele é um número inteiro e positivo. Portanto, para que o produto acima
seja negativo, deveremos ter:
16 – 2n < 0, de onde vem 16 < 2n ou 2n > 16 ou n > 8.
Como n é um número inteiro positivo, deduzimos imediatamente que n = 9.
Portanto, a alternativa correta é a letra A.
2 - As medidas dos lados de um triângulo são expressas por x + 1, 2x , x2 - 5 e estão em P.A. , nesta ordem.
O perímetro do triângulo vale:
a) 8
b) 12
c) 15
*d) 24
e) 33
SOLUÇÃO:
Ora, se x + 1, 2x , x2 – 5 formam uma P.A. , podemos escrever:
2x – (x + 1) = (x2 – 5) – 2x
2x – x –1 + 5 – x2 + 2x = 0
3x + 4 – x2 = 0
Multiplicando por (-1) ambos os membros da igualdade acima, fica:
x2 – 3x – 4 = 0
Resolvendo a equação do segundo grau acima encontraremos x = 4 ou x = - 1.
Assim, teremos:
x = 4: os termos da P.A . serão: x+1, 2x, x2 – 5 ou substituindo o valor de x encontrado: 5, 8, 11, que são as
medidas dos lados do triângulo. Portanto, o perímetro do triângulo (soma das medidas dos lados) será igual
a 5+8+11 = 24.
O valor negativo de x não serve ao problema, já que levaria a valores negativos para os lados do triângulo, o
que é uma impossibilidade matemática, pois as medidas dos lados de um triângulo são necessariamente
positivas. Portanto, a alternativa correta é a letra D.
3 - UFBA - Um relógio que bate de hora em hora o número de vezes correspondente a cada hora, baterá , de
zero às 12 horas x vezes. Calcule o dobro da terça parte de x.
Resp: 60
SOLUÇÃO:
Teremos que:
0 hora o relógio baterá 12 vezes. (Você não acha que bateria 0 vezes, não é?).
1 hora o relógio baterá 1 vez
2 horas o relógio baterá 2 vezes
3 horas o relógio baterá 3 vezes
....................................................
....................................................

12 horas o relógio baterá 12 vezes.
Logo, teremos a seguinte seqüência:
(12, 1, 2, 3, 4, 5, ... , 12)
A partir do segundo termo da seqüência acima, temos uma PA de 12 termos, cujo primeiro termo é igual a
1, a razão é 1 e o último termo é 12.
Portanto, a soma dos termos desta PA será:
S = (1 + 12).(12/2) = 13.6 = 78
A soma procurada será igual ao resultado anterior (a PA em vermelho acima) mais as 12 batidas da zero
hora. Logo, o número x será igual a x = 78 + 12 = 90.
Logo, o dobro da terça parte de x será: 2. (90/3) = 2.30 = 60, que é a resposta do problema proposto.
4 - UFBA - Numa progressão aritmética, o primeiro termo é 1 e a soma do n-ésimo termo com o número de
termos é 2. Calcule a razão dessa progressão.
Resp: r = -1
SOLUÇÃO:
Temos: a1 = 1 e an + n = 2, onde an é o n-ésimo termo.
Fazendo n = 2, vem: a2 + 2 = 2, de onde vem imediatamente que a2 = 0.
Daí, r = a2 – a1 = 0 – 1 = -1, que é a resposta procurada.
5 - A soma dos múltiplos positivos de 8 formados por 3 algarismos é:
a) 64376
b) 12846
c) 21286
d) 112
*e) 61376
SOLUÇÃO:
Números com 3 algarismos: de 100 a 999.
Primeiro múltiplo de 8 maior do que 100 = 104 (que é igual a 8x13)
Maior múltiplo de 8 menor do que 999 = 992 (que é igual a 8x124)
Temos então a PA: (104, 112, 120, 128, 136, ... , 992).
Da fórmula do termo geral an = a1 + (n – 1) . r poderemos escrever:
992 = 104 + (n – 1).8, já que a razão da PA é 8.
Daí vem: n = 112
Aplicando a fórmula da soma dos n primeiros termos de uma PA, teremos finalmente:
Sn = S112 = (104 + 992).(112/2) = 61376
A alternativa correta é portanto, a letra E.
6 – Determinar o centésimo termo da progressão aritmética na qual a soma do terceiro termo com o sétimo
é igual a 30 e a soma do quarto termo com o nono é igual a 60.
Resp: 965
SOLUÇÃO:
Podemos escrever:
a3 + a7 = 30
a4 + a9 = 60

Usando a fórmula do termo geral, poderemos escrever:
a1 + 2r + a1 + 6r = 30 ou 2.a1 + 8r = 30
a1 + 3r + a1 + 8r = 60 ou 2.a1 + 11r = 60
Subtraindo membro a membro as duas expressões em negrito, vem:
3r = 30 , de onde concluímos que a razão é igual a r = 10.
Substituindo numa das equações em negrito acima, vem:
2.a1 + 8.10 = 30, de onde tiramos a1 = - 25.
Logo, o centésimo termo será:
a100 = a1 + 99r = - 25 + 99.10 = 965
Entenderemos por progressão geométrica - PG - como qualquer seqüência de números reais ou complexos,
onde cada termo a partir do segundo, é igual ao anterior, multiplicado por uma constante denominada
razão.
Exemplos:
(1,2,4,8,16,32, ... ) PG de razão 2
(5,5,5,5,5,5,5, ... ) PG de razão 1
(100,50,25, ... ) PG de razão 1/2
(2,-6,18,-54,162, ...) PG de razão -3
2 - Fórmula do termo geral
Seja a PG genérica: (a1, a2, a3, a4, ... , a n, ... ) , onde a1 é o primeiro termo, e an é o n-ésimo termo, ou seja,
o termo de ordem n. Sendo q a razão da PG, da definição podemos escrever:
a2 = a1 . q
a3 = a2 . q = (a1 . q) . q = a1 . q2
a4 = a3 . q = (a1 . q2) . q = a1 . q3
................................................
................................................
Infere-se (deduz-se) que: an = a1 . qn-1 , que é denominada fórmula do termo geral da PG.
Genericamente, poderemos escrever: aj = ak . qj-k
Exemplos:
a) Dada a PG (2,4,8,... ), pede-se calcular o décimo termo.
Temos: a1 = 2, q = 4/2 = 8/4 = ... = 2. Para calcular o décimo termo ou seja a10, vem pela fórmula:
a10 = a1 . q9 = 2 . 29 = 2. 512 = 1024
b) Sabe-se que o quarto termo de uma PG crescente é igual a 20 e o oitavo termo é igual a 320. Qual a razão
desta PG?
Temos a4 = 20 e a8 = 320. Logo, podemos escrever: a8 = a4 . q8-4 . Daí, vem: 320 = 20.q4
Então q4 =16 e portanto q = 2.
Nota: Uma PG genérica de 3 termos, pode ser expressa como:

(x/q, x, xq), onde q é a razão da PG.
3 - Propriedades principais
P1 - em toda PG, um termo é a média geométrica dos termos imediatamente anterior e posterior.
Exemplo: PG (A,B,C,D,E,F,G)
Temos então: B2 = A . C ; C2 = B . D ; D2 = C . E ; E2 = D . F etc.
P2 - o produto dos termos eqüidistantes dos extremos de uma PG é constante.
Exemplo: PG ( A,B,C,D,E,F,G)
Temos então: A . G = B . F = C . E = D . D = D2
4 - Soma dos n primeiros termos de uma PG
Seja a PG (a1, a2, a3, a4, ... , an , ...) . Para o cálculo da soma dos n primeiros termos Sn , vamos considerar o
que segue:
Sn = a1 + a2 + a3 + a4 + ... + an-1 + an
Multiplicando ambos os membros pela razão q vem:
Sn . q = a1 . q + a2 .q + .... + an-1 . q + an .q .
Logo, conforme a definição de PG, podemos reescrever a expressão acima como:
Sn . q = a2 + a3 + ... + an + an . q
Observe que a2 + a3 + ... + an é igual a Sn - a1 . Logo, substituindo, vem:
Sn . q = Sn - a1 + an . q
Daí, simplificando convenientemente, chegaremos à seguinte fórmula da soma:
Se substituirmos a n = a1 . qn-1 , obteremos uma nova apresentação para a fórmula da soma, ou seja:
Exemplo:
Calcule a soma dos 10 primeiros termos da PG (1,2,4,8,...)
Temos:
Observe que neste caso a1 = 1.
5 - Soma dos termos de uma PG decrescente e ilimitada
Considere uma PG ILIMITADA ( infinitos termos) e decrescente. Nestas condições, podemos considerar
que no limite teremos an = 0. Substituindo na fórmula anterior, encontraremos:
Exemplo:

Resolva a equação: x + x/2 + x/4 + x/8 + x/16 + ... =100
Ora, o primeiro membro é uma PG de primeiro termo x e razão 1/2. Logo, substituindo na fórmula, vem:
Daí, vem: x = 100 . 1/2 = 50
6 – Exercícios resolvidos e propostos
6.1 - Se a soma dos tres primeiros termos de uma PG decrescente é 39 e o seu produto é 729 , então sendo a,
b e c os tres primeiros termos , pede-se calcular o valor de a2 + b2 + c2 .
Solução:
Sendo q a razão da PG, poderemos escrever a sua forma genérica: (x/q, x, xq).
Como o produto dos 3 termos vale 729, vem:
x/q . x . xq = 729 de onde concluímos que:
x3 = 729 = 36 = 33 . 33 = 93 , logo, x = 9.
Portanto a PG é do tipo: 9/q, 9, 9q
É dado que a soma dos 3 termos vale 39, logo:
9/q + 9 + 9q = 39 de onde vem: 9/q + 9q – 30 = 0
Multiplicando ambos os membros por q, fica:
9 + 9q2 – 30q = 0
Dividindo por 3 e ordenando, fica:
3q2 – 10q + 3 = 0, que é uma equação do segundo grau.
Resolvendo a equação do segundo grau acima encontraremos q = 3 ou q = 1/3.
Como é dito que a PG é decrescente, devemos considerar apenas o valor
q = 1/3, já que para q = 3, a PG seria crescente.
Portanto, a PG é:
9/q, 9, 9q, ou substituindo o valor de q vem: 27, 9, 3.
O problema pede a soma dos quadrados, logo:
a2 + b2 + c2 = 272 + 92 + 32 = 729 + 81 + 9 = 819
6.2 - Sabe-se que S = 9 + 99 + 999 + 9999 + ... + 999...9 onde a última parcela contém n algarismos. Nestas
condições, o valor de 10n+1 - 9(S + n) é:
A)1
*B) 10
C) 100
D) -1
E) -10
Solução:
Observe que podemos escrever a soma S como:
S = (10 – 1) + (100 – 1) + (1000 – 1) + (10000 – 1) + ... + (10n – 1)
S = (10 – 1) + (102 – 1) + (103 – 1) + (104 – 1) + ... + (10n – 1)

Como existem n parcelas, observe que o número (– 1) é somado n vezes,
resultando em n(-1) = - n.
Logo, poderemos escrever:
S = (10 + 102 + 103 + 104 + ... + 10n ) – n
Vamos calcular a soma Sn = 10 + 102 + 103 + 104 + ... + 10n , que é uma PG de primeiro termo a1 = 10,
razão q = 10 e último termo an = 10n . Teremos:
Sn = (an.q – a1) / (q –1) = (10n . 10 – 10) / (10 – 1) = (10n+1 – 10) / 9
Substituindo em S, vem:
S = [(10n+1 – 10) / 9] – n
Deseja-se calcular o valor de 10n+1 - 9(S + n)
Temos que S + n = [(10n+1 – 10) / 9] – n + n = (10n+1 – 10) / 9
Substituindo o valor de S + n encontrado acima, fica:
10n+1 – 9(S + n) = 10n+1 – 9(10n+1 – 10) / 9 = 10n+1 – (10n+1 – 10) = 10
6.3 - O limite da expressão onde x é positivo, quando o número de radicais aumenta
indefinidamente
é igual a:
A)1/x
*B) x
C) 2x
D) n.x
E) 1978x
Solução:
Observe que a expressão dada pode ser escrita como:
x1/2. x1/4 . x1/8 . x1/16 . ... = x1/2 + 1 / 4 + 1/8 + 1/16 + ...
O expoente é a soma dos termos de uma PG infinita de primeiro termo a1 = 1 /2 e
razão q = 1 /2. Logo, a soma valerá: S = a1 / (1 – q) = (1 /2) / 1 – (1 /2) = 1
Então, x1/2 + 1 / 4 + 1/8 + 1/16 + ... = x1 = x
6.4 - UEFS - Os números que expressam os ângulos de um quadrilátero, estão em progressão geométrica de
razão 2. Um desses ângulos mede:
a) 28°
b) 32°
c) 36°
*d) 48°
e) 50°
Solução:
Seja x o menor ângulo interno do quadrilátero em questão. Como os ângulos estão em Progressão
Geométrica de razão 2, podemos escrever a PG de 4 termos:

( x, 2x, 4x, 8x ).
Ora, a soma dos ângulos internos de um quadrilátero vale 360º . Logo,
x + 2x + 4x + 8x = 360º
15.x = 360º
Portanto, x = 24º . Os ângulos do quadrilátero são, portanto: 24º, 48º, 96º e 192º.
O problema pede um dos ângulos. Logo, alternativa D.
PROBABILIDADE
A história da teoria das probabilidades, teve início com os jogos de cartas, dados e de roleta. Esse é o
motivo da grande existência de exemplos de jogos de azar no estudo da probabilidade. A teoria da
probabilidade permite que se calcule a chance de ocorrência de um número em um experimento aleatório.
Experimento Aleatório
É aquele experimento que quando repetido em iguais condições, podem fornecer resultados diferentes,
ou seja, são resultados explicados ao acaso. Quando se fala de tempo e possibilidades de ganho na loteria, a
abordagem envolve cálculo de experimento aleatório.
Espaço Amostral
É o conjunto de todos os resultados possíveis de um experimento aleatório. A letra que representa o
espaço amostral, é S.
Exemplo:
Lançando uma moeda e um dado, simultaneamente, sendo S o espaço amostral, constituído pelos 12
elementos:
S = {K1, K2, K3, K4, K5, K6, R1, R2, R3, R4, R5, R6}
1. Escreva explicitamente os seguintes eventos: A={caras e m número par aparece}, B={um número
primo aparece}, C={coroas e um número ímpar aparecem}.
2. Idem, o evento em que:
a) A ou B ocorrem;
b) B e C ocorrem;
c) Somente B ocorre.
3. Quais dos eventos A,B e C são mutuamente exclusivos
Resolução:
1. Para obter A, escolhemos os elementos de S constituídos de um K e um número par: A={K2, K4,
K6};
Para obter B, escolhemos os pontos de S constituídos de números primos: B={K2,K3,K5,R2,R3,R5}
Para obter C, escolhemos os pontos de S constituídos de um R e um número ímpar: C={R1,R3,R5}.
2. (a) A ou B = AUB = {K2,K4,K6,K3,K5,R2,R3,R5}

(b) B e C = B Ç C = {R3,R5}
(c) Escolhemos os elementos de B que não estão em A ou C;
B Ç Ac Ç Cc = {K3,K5,R2}
3. A e C são mutuamente exclusivos, porque A Ç C = Æ
Conceito de probabilidade
Se em um fenômeno aleatório as possibilidades são igualmente prováveis, então a probabilidade de ocorrer
um evento A é:
Por, exemplo, no lançamento de um dado, um número par pode ocorrer de 3 maneiras diferentes dentre 6
igualmente prováveis, portanto, P = 3/6= 1/2 = 50%
Dizemos que um espaço amostral S (finito) é equiprovável quando seus eventos elementares têm
probabilidades iguais de ocorrência.
Num espaço amostral equiprovável S (finito), a probabilidade de ocorrência de um evento A é sempre:
Propriedades Importantes:
1. Se A e A’ são eventos complementares, então:
P( A ) + P( A' ) = 1
2. A probabilidade de um evento é sempre um número entre Æ (probabilidade de evento impossível) e 1
(probabilidade do evento certo).
Probabilidade Condicional
Antes da realização de um experimento, é necessário que já tenha alguma informação sobre o evento que se
deseja observar. Nesse caso, o espaço amostral se modifica e o evento tem a sua probabilidade de ocorrência
alterada.
Fórmula de Probabilidade Condicional
P(E1 e E2 e E3 e ...e En-1 e En) é igual a P(E1).P(E2/E1).P(E3/E1 e E2)...P(En/E1 e E2 e ...En-1).
Onde P(E2/E1) é a probabilidade de ocorrer E2, condicionada pelo fato de já ter ocorrido E1;
P(E3/E1 e E2) é a probabilidade ocorrer E3, condicionada pelo fato de já terem ocorrido E1 e E2;

P(Pn/E1 e E2 e ...En-1) é a probabilidade de ocorrer En, condicionada ao fato de já ter ocorrido E1 e
E2...En-1.
Exemplo:
Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se ocorrer um sorteio de 2 bolas, uma de cada vez
e sem reposição, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?
Resolução:
Seja o espaço amostral S=30 bolas, e considerarmos os seguintes eventos:
A: vermelha na primeira retirada e P(A) = 10/30
B: azul na segunda retirada e P(B) = 20/29
Assim:
P(A e B) = P(A).(B/A) = 10/30.20/29 = 20/87
Eventos independentes
Dizemos que E1 e E2 e ...En-1, En são eventos independentes quando a probabilidade de ocorrer um
deles não depende do fato de os outros terem ou não terem ocorrido.
Fórmula da probabilidade dos eventos independentes:
P(E1 e E2 e E3 e ...e En-1 e En) = P(E1).P(E2).p(E3)...P(En)
Exemplo:
Uma urna tem 30 bolas, sendo 10 vermelhas e 20 azuis. Se sortearmos 2 bolas, 1 de cada vez e repondo a
sorteada na urna, qual será a probabilidade de a primeira ser vermelha e a segunda ser azul?
Resolução:
Como os eventos são independentes, a probabilidade de sair vermelha na primeira retirada e azul na
segunda retirada é igual ao produto das probabilidades de cada condição, ou seja, P(A e B) = P(A).P(B). Ora,
a probabilidade de sair vermelha na primeira retirada é 10/30 e a de sair azul na segunda retirada 20/30.
Daí, usando a regra do produto, temos: 10/30.20/30=2/9.
Observe que na segunda retirada forma consideradas todas as bolas, pois houve reposição. Assim, P(B/A)
=P(B), porque o fato de sair bola vermelha na primeira retirada não influenciou a segunda retirada, já que
ela foi reposta na urna.
Probabilidade de ocorrer a união de eventos
Fórmula da probabilidade de ocorrer a união de eventos:
P(E1 ou E2) = P(E1) + P(E2) - P(E1 e E2)
De fato, se existirem elementos comuns a E1 e E2, estes eventos estarão computados no cálculo de P(E1) e
P(E2). Para que sejam considerados uma vez só, subtraímos P(E1 e E2).

Fórmula de probabilidade de ocorrer a união de eventos mutuamente exclusivos:
P(E1 ou E2 ou E3 ou ... ou En) = P(E1) + P(E2) + ... + P(En)
Exemplo: Se dois dados, azul e branco, forem lançados, qual a probabilidade de sair 5 no azul e 3 no
branco?
Considerando os eventos:
A: Tirar 5 no dado azul e P(A) = 1/6
B: Tirar 3 no dado branco e P(B) = 1/6
Sendo S o espaço amostral de todos os possíveis resultados, temos:
n(S) = 6.6 = 36 possibilidades. Daí, temos:P(A ou B) = 1/6 + 1/6 – 1/36 = 11/36
Exemplo: Se retirarmos aleatoriamente uma carta de baralho com 52 cartas, qual a probabilidade de ser um
8 ou um Rei?
Sendo S o espaço amostral de todos os resultados possíveis, temos: n(S) = 52 cartas. Considere os eventos:
A: sair 8 e P(A) = 4/52
B: sair um rei e P(B) = 4/52
Assim, P(A ou B) = 4/52 + 4/52 – 0 = 8/52 = 2/13. Note que P(A e B) = 0, pois uma carta não pode ser 8 e rei
ao mesmo tempo. Quando isso ocorre dizemos que os eventos A e B são mutuamente exclusivos
Matrizes
Elementos básicos para a construção de matrizes
Aqui tomaremos o conjunto N dos números naturais, como:
N={1,2,3,4,5,6,7,...}
O produto cartesiano N×N indicará o conjunto de todos os pares ordenados da forma (a,b), onde a e b são
números naturais, isto é:
N×N={(a,b): a e b são números naturais }
Uma relação importante em N×N é:
Smn={(i,j): 1<i<m, 1<j<n}
Definição de matriz
Uma matriz real (ou complexa) é uma função que a cada par ordenado (i,j) no conjunto Smn associa um
número real (ou complexo).
Uma forma comum e prática para representar uma matriz definida na forma acima é através de uma tabela
contendo m×n números reais (ou complexos). Identificaremos a matriz abaixo com a letra A.

a(1,1)a(1,1)a(1,1)a(1,1) a(1,2)a(1,2)a(1,2)a(1,2) ............ a(1,n)a(1,n)a(1,n)a(1,n)
a(2,1)a(2,1)a(2,1)a(2,1) a(2,2)a(2,2)a(2,2)a(2,2) ............ a(2,n)a(2,n)a(2,n)a(2,n)
............ ............ ............ ............
a(m,1)a(m,1)a(m,1)a(m,1) a(m,2)a(m,2)a(m,2)a(m,2) ............ a(m,n)a(m,n)a(m,n)a(m,n)
Definições básicas sobre matrizes
1. Ordem: Se a matriz A tem m linhas e n colunas, dizemos que a ordem da matriz é m×n.
2. Posição de um elemento: Na tabela acima a posição de cada elemento aij=a(i,j) é indicada pelo par
ordenado (i,j).
3. Notação para a matriz: Indicamos uma matriz A pelos seus elementos, na forma: A=[a(i,j)].
4. Diagonal principal: A diagonal principal da matriz é indicada pelos elementos da forma a(i,j) onde
i=j.
5. Matriz quadrada é a matriz que tem o número de linhas igual ao número de colunas, i.e., m=n.
6. A diagonal secundária de uma matriz quadrada de ordem n é indicada pelos n elementos:
a(1,n), a(2,n-1), a(3,n-2), a(4,n-3), a(5,n-4), ..., a(n-1,2), a(n,1)
7. Matriz diagonal é a que tem elementos nulos fora da diagonal principal.
8. Matriz real é aquela que tem números reais como elementos.
9. Matriz complexa é aquela que tem números complexos como elementos.
10.Matriz nula é aquela que possui todos os elementos iguais a zero.
11.Matriz identidade, denotada por Id, tem os elementos da diagonal principal iguais a 1 e zero fora da
diagonal principal.
12.Matriz diagonal é aquela que tem todos os elementos nulos fora da diagonal principal. Alguns
elementos da diagonal principal podem ser nulos.
Exemplos de matrizes
Matriz 4x4 de números reais:
12121212 -6-6-6-6 7777 18181818
-23-23-23-23 -24-24-24-24 0000 0000
0000 0000 5555 0000
0000 0000 0000 9999
Matriz 4x4 de números complexos:
12121212 -6+i-6+i-6+i-6+i 7777 iiii
-i-i-i-i -24-24-24-24 0000 0000
0000 0000 5+i5+i5+i5+i 5-i5-i5-i5-i

0000 0000 0000 9999
Matriz nula com duas linhas e duas colunas:
0000 0000
0000 0000
Matriz nula com três linhas e duas colunas:
0000 0000
0000 0000
0000 0000
Matriz identidade com três linhas e três colunas:
1111 0000 0000
0000 1111 0000
0000 0000 1111
Matriz diagonal com quatro linhas e quatro colunas:
23232323 0000 0000 0000
0000 -56-56-56-56 0000 0000
0000 0000 0000 0000
0000 0000 0000 100100100100
Matrizes iguais
Duas matrizes A=[a(i,j)] e B=[b(i,j)], de mesma ordem m×n, são iguais se todos os seus correspondentes
elementos são iguais, isto é:
a(i,j) = b(i,j)
para todo par ordenado (i,j) em Smn.
Exercício: Determinar os valores de x e y para que sejam iguais as matrizes abaixo, isto é:
1111 2222
3333 4444
====
x-1x-1x-1x-1 y-1y-1y-1y-1
x+yx+yx+yx+y x2x2x2x2
Soma de matrizes e suas propriedades
A soma (adição) de duas matrizes A=[a(i,j)] e B=[b(i,j)] de mesma ordem m×n, é uma outra matriz C=[c(i,j)],
definida por:
c(i,j) = a(i,j) + b(i,j)

Exemplo: A soma das matrizes A e B é a terceira matriz indicada abaixo.
-23-23-23-23 10101010
7777 9999
++++
10101010 5555
8888 9999
====
-13-13-13-13 15151515
15151515 18181818
Propriedades da soma de matrizes
A1: Associativa: Para quaisquer matrizes A, B e C, de mesma ordem m×n, vale a igualdade:
(A + B) + C = A + (B + C)
A2: Comutativa: Para quaisquer matrizes A e B, de mesma ordem m×n, vale a igualdade:
A + B = B + A
A3: Elemento neutro: Existe uma matriz nula 0 que somada com qualquer outra matriz A de mesma ordem,
fornecerá a própria matriz A, isto é:
0 + A = A
A4: Elemento oposto: Para cada matriz A, existe uma matriz -A, denominada a oposta de A, cuja soma entre
ambas fornecerá a matriz nula de mesma ordem, isto é:
A + (-A) = 0
Multiplicação de escalar por matriz e suas propriedades
Seja k um escalar e A=[a(i,j)] uma matriz. Definimos a multiplicação do escalar k pela matriz A, como uma
outra matriz C=k.A, definida por:
c(i,j) = k. a(i,j)
Exemplo: A multiplicação do escalar -4 pela matriz A, definida por:
-4-4-4-4
-2-2-2-2 10101010
7777 9999
====
-8-8-8-8 -40-40-40-40
28282828 36363636
Propriedades da multiplicação de escalar por matriz
E1: Multiplicação pelo escalar 1: A multiplicação do escalar 1 por qualquer matriz A, fornecerá a própria
matriz A, isto é:
1.A = A
E2: Multiplicação pelo escalar zero: A multiplicação do escalar 0 por qualquer matriz A, fornecerá a matriz

nula, isto é:
0.A = 0
E3: Distributividade das matrizes: Para quaisquer matrizes A e B de mesma ordem e para qualquer escalar k,
tem-se:
k (A+B) = k A + k B
E4: Distributividade dos escalares: Para qualquer matriz A e para quaisquer escalares p e q, tem-se:
(p + q) A = p A + q A
Multiplicação de matrizes
Seja a matriz A=[a(i,j)] de ordem m×n e a matriz B=(b(k,l)) de ordem nxr. Definimos o produto das matrizes
A e B como uma outra matriz C=A.B, definida por:
c(u,v) = a(u,1) b(1,v) + a(u,2) b(2,v) + ... + a(u,m) b(m,v)
para todo par (u,v) em Smr.
Para obter o elemento da 2a. linha e 3a. coluna da matriz produto C=A.B, isto é, o elemento c(2,3),
devemos:
1. multiplicar os primeiros elementos da 2a. linha e 3a. coluna;
2. multiplicar os segundos elementos da 2a. linha e 3a. coluna;
3. multiplicar os terceiros elementos da 2a. linha e 3a. coluna;
4. multiplicar os quartos elementos da 2a. linha e 3a. coluna;
5. somar os quatro produtos obtidos anteriomente.
Assim:
c23 = a21 b13 + a22 b23 + a23 b33 + a24 b43
Podemos visualizar esta operação através das matrizes seguintes. Basta observar a linha em azul na primeira
matriz, a coluna em azul na segunda matriz e o elemento em azul na terceira matriz.
a11a11a11a11 a12a12a12a12 a13a13a13a13 a14a14a14a14
××××
b1b1b1b1
1111
b1b1b1b1
2222
b1b1b1b1
3333
b14b14b14b14
b2b2b2b2
1111
b2b2b2b2
2222
b2b2b2b2
3333
b24b24b24b24
b3b3b3b3
1111
b3b3b3b3
2222
b3b3b3b3
3333
b34b34b34b34
b4b4b4b4
1111
b4b4b4b4
2222
b4b4b4b4
3333
b44b44b44b44
====
c1c1c1c1
1111
c1c1c1c1
2222
c1c1c1c1
3333
c14c14c14c14
c2c2c2c2
1111
c2c2c2c2
2222
c2c2c2c2
3333
c24c24c24c24
c3c3c3c3
1111
c3c3c3c3
2222
c3c3c3c3
3333
c34c34c34c34
c4c4c4c4
1111
c4c4c4c4
2222
c4c4c4c4
3333
c44c44c44c44
Observação: Somente podemos multiplicar duas matrizes se o número de colunas da primeira for igual ao
número de linhas da segunda.

Propriedades da multiplicação de matrizes
Para todas as matrizes A, B e C que podem ser multiplicadas, temos algumas propriedades:
M1: Nem sempre vale a comutatividade: Em geral, A×B é diferente de B×A, como é o caso do produto que
segue, onde A está cor vermelha e B em cor preta:
1111 2222 3333
2222 4444 6666
3333 6666 9999
××××
1111 2222
3333 5555
7777 9999
M2: Distributividade da soma à direita
A (B+C) = A B + A C
M3: Distributividade da soma à esquerda
(A + B) C = A C + B C
M4: Associatividade
A (B C) = (A B) C
M5: Nulidade do produto: Pode acontecer que o produto de duas matrizes seja a matriz nula, isto é: AB=0,
embora nem A nem B sejam matrizes nulas, como é o caso do produto:
0000 1111
0000 0000
××××
0000 2222
0000 0000
====
0000 0000
0000 0000
M6: Nem sempre vale o cancelamento: Se ocorrer a igualdade AC=BC, então nem sempre será verdadeiro
que A=B, pois existem exemplos de matrizes como as apresentadas abaixo, tal que:
0000 1111
0000 0000
××××
0000 5555
0000 0000
====
0000 2222
0000 0000
××××
0000 5555
0000 0000
mas as matrizes A e B são diferentes.
Matrizes com propriedades especiais
1. Uma matriz A é nilpotente de índice k natural, se:
Ak = 0
2. Uma matriz A é periódica de índice k natural, se:
Ak+1= A

3. Uma matriz A é idempotente, se:
A2 = A
4. As matrizes A e B são comutativas, se:
A B = B A
5. As matrizes A e B são anti-comutativas, se:
A B = - B A
6. A matriz identidade Id multiplicada por toda matriz A, fornecerá a própria matriz A, quando o
produto fizer sentido.
Id A = A
7. A matriz A será a inversa da matriz B, se:
A B = Id e B A = Id
A transposta de uma matriz e suas propriedades
Dada uma matriz A=[a(i,j)] de ordem m×n, definimos a transposta da matriz A como a matriz
At = [a(j,i)]
e segue que as linhas de A se transformam nas colunas de At.
Propriedades das matrizes transpostas
T1: A transposta da transposta da matriz é a própria matriz.
(At)t = A
T2: A transposta da multiplicação de um escalar por uma matriz é igual ao próprio escalar multiplicado pela
transposta da matriz.
(kA)t = k (At)
T3: A transposta da soma de duas matrizes é a soma das transpostas dessas matrizes.
(A + B)t = At + Bt
T4: A transposta do produto de duas matrizes é igual ao produto das transpostas das matrizes na ordem
trocada.
(A B)t = Bt At
Matrizes simétricas e anti-simétricas e suas propriedades
Uma matriz A é simétrica se é uma matriz quadrada tal que:
At = A
Uma matriz A é anti-simétrica se é uma matriz quadrada tal que:
At = -A

Propriedades das matrizes simétricas e anti-simétricas
S1: Se A é uma matriz simétrica de ordem n, então para todo escalar k, a matriz k.A é simétrica.
S2: Se A é uma matriz quadrada de ordem n, então a matriz B=A+At é simétrica.
S3: Se A é uma matriz quadrada de ordem n, então a matriz B=A-At é anti-simétrica.
S4: Se A é uma matriz quadrada de ordem n, então A sempre pode ser decomposta como a soma de uma
matriz simétrica S com uma matriz anti-simétrica T, isto é, A=S+T, e neste caso:
S =(1/2)(A + At) e T =(1/2)(A - At)
Sistemas Lineares
As equações lineares assim como os sistemas de equações são muito utilizados no cotidiano das pessoas.
Exemplo: Uma companhia de navegação tem três tipos de recipientes A, B e C, que carrega cargas em
containers de três tipos I, II e III. As capacidades dos recipientes são dadas pela matriz:
Tipo do RecipienteTipo do RecipienteTipo do RecipienteTipo do Recipiente IIII IIIIIIII IIIIIIIIIIII
AAAA 4444 3333 2222
BBBB 5555 2222 3333
CCCC 2222 2222 3333
Quais são os números de recipientes x1, x2 e x3 de cada categoria A, B e C, se a companhia deve transportar
42 containers do tipo I, 27 do tipo II e 33 do tipo III?
Montagem do sistema linear
4 x1 + 5 x2 + 2 x3 = 42
3 x1 + 3 x2 + 2 x3 = 27
2 x1 + 2 x2 + 2 x3 = 33
Arthur Cayley (1821-1895): Matemático inglês nascido em Richmond, diplomou-se no Trinity College de
Cambridge. Na sua vida, Cayley encontrou rivais em Euler e Cauchy sendo eles os três maiores produtores
de materiais no campo da Matemática. Em 1858, Cayley apresentou representações por matrizes. Segundo
ele, as matrizes são desenvolvidas a partir da noção de determinante, isto é, a partir do exame de sistemas de
equações, que ele denominou: o sistema. Cayley desenvolveu uma Álgebra das matrizes quadradas em
termos de transformações lineares homogêneas.
Equação linear
É uma equação da forma
a11 x1 + a12 x2 + a13 x3 + ... + a1n xn = b1
onde

 x1, x2, ..., xn são as incógnitas;
 a11, a12, ...,a1n são os coeficientes (reais ou complexos);
 b1 é o termo independente (número real ou complexo).
Exemplos de equações lineares
1. 4 x + 3 y - 2 z = 0
2. 2 x - 3 y + 0 z - w = -3
3. x1 - 2 x2 + 5 x3 = 1
4. 4i x + 3 y - 2 z = 2-5i
Notação: Usamos R[x] para a raiz quadrada de x>0.
Exemplos de equações não-lineares
1. 3 x + 3y R[x] = -4
2. x2 + y2 = 9
3. x + 2 y - 3 z w = 0
4. x2 + y2 = -9
Solução de uma equação linear
Uma sequência de números reais (r1,r2,r3,r4) é solução da equação linear
a11 x1 + a12 x2 + a13 x3 + a14 x4 = b1
se trocarmos cada xi por ri na equação e este fato implicar que o membro da esquerda é identicamente igual
ao membro da direita, isto é:
a11 r1 + a12 r2 + a13 r3 + a14 r4 = b1
Exemplo: A sequência (5,6,7) é uma solução da equação 2x+3y-2z=14 pois, tomando x=5, y=6 e z=7 na
equação dada, teremos:
2×5 + 3×6 - 2×7 = 14
Sistemas de equações lineares
Um sistema de equações lineares ou sistema linear é um conjunto formado por duas ou mais equações
lineares. Um sistema linear pode ser representado na forma:
a11 x1 + a12 x2 +...+ a1n xn = b1
a21 x1 + a22 x2 +...+ a2n xn = b2
... ... ... ...
am1 x1 + am2 x2 +...+ amn xn = bn
onde
 x1, x2, ..., xn são as incógnitas;

 a11, a12, ..., amn são os coeficientes;
 b1, b2, ..., bm são os termos independentes.
Solução de um sistema de equações lineares
Uma sequência de números (r1,r2,...,rn) é solução do sistema linear:
a11 x1 + a12 x2 +...+ a1n xn = b1
a21 x1 + a22 x2 +...+ a2n xn = b2
... ... ... ...
am1 x1 + am2 x2 +...+ amn xn = bn
se satisfaz identicamente a todas as equações desse sistema linear.
Exemplo: O par ordenado (2,0) é uma solução do sistema linear:
2x + y = 4
x + 3y = 2
x + 5y = 2
pois satisfaz identicamente a todas as equações do mesmo, isto é, se substituirmos x=2 e y=0, os dois
membros de cada igualdade serão iguais em todas as equações.
Consistência de Sistemas Lineares
O número de soluções de um sistema linear determina a sua classificação de duas maneiras com relação à
sua consistência:
Sistema possível ou consistente: Quando tem pelo menos uma solução.
a. Se tem uma única solução, o sistema é determinado.
b. Se tem mais que uma solução, o sistema é indeterminado.
Sistema impossível ou inconsistente: Se não admite qualquer solução.
Exemplos de sistemas com respeito às suas soluções
Sistema com uma única solução: As equações lineares abaixo representam duas retas no plano cartesiano
que têm o ponto (3,-2) como interseção.
x + 2y = -1
2x - y = 8
Sistema com infinitas soluções: As equações lineares representam retas paralelas sobrepostas no plano
cartesiano, logo existem infinitos pontos que satisfazem a ambas as equações (pertencem a ambas as retas).
4x + 2y = 100
8x + 4y = 200
Sistema que não tem solução: As equações lineares representam retas paralelas no plano cartesiano, logo,
não existem pontos que pertençam às duas retas.

x + 3y = 4
x + 3y = 5
Sistemas equivalentes
Dois sistemas são equivalentes se admitem a mesma solução.
Exemplo: São equivalentes os sistemas S1 e S2 indicados abaixo:
S1S1S1S1
3x + 6y = 423x + 6y = 423x + 6y = 423x + 6y = 42
2x - 4y = 122x - 4y = 122x - 4y = 122x - 4y = 12
S2S2S2S2
1x + 2y = 141x + 2y = 141x + 2y = 141x + 2y = 14
1x - 2y =1x - 2y =1x - 2y =1x - 2y = 6666
pois eles admitem a mesma solução x=10 e y=2.
Notação: Quando dois sistemas S1 e S2 são equivalentes, usamos a notação S1~S2.
Operações elementares sobre sistemas lineares
Existem três tipos de operações elementares que podem ser realizadas sobre um sistema linear de equações
de forma a transformá-lo em um outro sistema equivalente mais simples que o anterior. Na sequência
trabalharemos com um exemplo para mostrar como funcionam essas operações elementares sobre linhas. O
segundo sistema (o que aparece à direita) já mostra o resultado da ação da operação elementar. Nas linhas
iniciais de cada tabela, você encontra a operação que foi realizada.
1. Troca de posição de duas equações do sistema
Troca a Linha 1 com a Linha 3Troca a Linha 1 com a Linha 3Troca a Linha 1 com a Linha 3Troca a Linha 1 com a Linha 3
x + 2y - z = 2x + 2y - z = 2x + 2y - z = 2x + 2y - z = 2
2x-3y+2z=02x-3y+2z=02x-3y+2z=02x-3y+2z=0
4x + y - 5z = 94x + y - 5z = 94x + y - 5z = 94x + y - 5z = 9
~~~~
4x + y - 5z = 94x + y - 5z = 94x + y - 5z = 94x + y - 5z = 9
2x-3y+2z=02x-3y+2z=02x-3y+2z=02x-3y+2z=0
x + 2y - z = 2x + 2y - z = 2x + 2y - z = 2x + 2y - z = 2
2. Multiplicação de uma equação por um número não nulo
Multiplica a Linha 1 pelo número 3Multiplica a Linha 1 pelo número 3Multiplica a Linha 1 pelo número 3Multiplica a Linha 1 pelo número 3
x + 2y - z = 2x + 2y - z = 2x + 2y - z = 2x + 2y - z = 2
2x-3y+2z=02x-3y+2z=02x-3y+2z=02x-3y+2z=0
4x+y-5z=94x+y-5z=94x+y-5z=94x+y-5z=9
~~~~
3x + 6y - 3z = 63x + 6y - 3z = 63x + 6y - 3z = 63x + 6y - 3z = 6
2x-3y+2z=02x-3y+2z=02x-3y+2z=02x-3y+2z=0
4x+y-5z=94x+y-5z=94x+y-5z=94x+y-5z=9
A equação resultante fica na linha 1A equação resultante fica na linha 1A equação resultante fica na linha 1A equação resultante fica na linha 1
3. Adição de duas equações do sistema
Adição da Linha 2 com a Linha 3Adição da Linha 2 com a Linha 3Adição da Linha 2 com a Linha 3Adição da Linha 2 com a Linha 3
x+2y-z=2x+2y-z=2x+2y-z=2x+2y-z=2
2x -3y + 2z = 02x -3y + 2z = 02x -3y + 2z = 02x -3y + 2z = 0
4x + y - 5z = 94x + y - 5z = 94x + y - 5z = 94x + y - 5z = 9
~~~~
3x+6y-3z=63x+6y-3z=63x+6y-3z=63x+6y-3z=6
2x-3y+2z=02x-3y+2z=02x-3y+2z=02x-3y+2z=0
6x - 2y - 3z = 96x - 2y - 3z = 96x - 2y - 3z = 96x - 2y - 3z = 9
A equação resultante fica na linha 3A equação resultante fica na linha 3A equação resultante fica na linha 3A equação resultante fica na linha 3

Resolução de sistemas lineares por escalonamento
Com o auxílio das três Operações Elementares sobre linhas, podemos resolver sistemas lineares. Vamos
mostrar como funciona este processo através de um exemplo.
Exemplo: Consideremos o sistema com 3 equações e 3 incógnitas.
3x + y + z = 20
2x - y - z = -15
-4x + y -5z = -41
Observação: Usamos Li+Lj->Lj para indicar a soma da linha i com a linha j com o resultado na linha j.
Usamos k Li->Li, para indicar que multiplicamos a linha i pela constante k e o resultado ficou na linha i.
Passo 1: L1-L2->L1Passo 1: L1-L2->L1Passo 1: L1-L2->L1Passo 1: L1-L2->L1
3x + 1y + 1z = 203x + 1y + 1z = 203x + 1y + 1z = 203x + 1y + 1z = 20
2x - 1y - 1z = -152x - 1y - 1z = -152x - 1y - 1z = -152x - 1y - 1z = -15
-4x+1y-5z=-41-4x+1y-5z=-41-4x+1y-5z=-41-4x+1y-5z=-41
~~~~
1x + 2y + 2z = 351x + 2y + 2z = 351x + 2y + 2z = 351x + 2y + 2z = 35
2x-1y-1z=-152x-1y-1z=-152x-1y-1z=-152x-1y-1z=-15
-4x+1y-5z=-41-4x+1y-5z=-41-4x+1y-5z=-41-4x+1y-5z=-41
Passo 2: L2-2.L1->L2Passo 2: L2-2.L1->L2Passo 2: L2-2.L1->L2Passo 2: L2-2.L1->L2
1x + 2y + 2z = 351x + 2y + 2z = 351x + 2y + 2z = 351x + 2y + 2z = 35
2x - 1y - 1z = -152x - 1y - 1z = -152x - 1y - 1z = -152x - 1y - 1z = -15
-4x+1y-5z=-41-4x+1y-5z=-41-4x+1y-5z=-41-4x+1y-5z=-41
~~~~
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x - 5y - 5z = -850x - 5y - 5z = -850x - 5y - 5z = -850x - 5y - 5z = -85
-4x+1y-5z=-41-4x+1y-5z=-41-4x+1y-5z=-41-4x+1y-5z=-41
Passo 3: L3+4.L1->L3Passo 3: L3+4.L1->L3Passo 3: L3+4.L1->L3Passo 3: L3+4.L1->L3
1x + 2y + 2z = 351x + 2y + 2z = 351x + 2y + 2z = 351x + 2y + 2z = 35
0x-5y-5z=-850x-5y-5z=-850x-5y-5z=-850x-5y-5z=-85
-4x + 1y - 5z = -41-4x + 1y - 5z = -41-4x + 1y - 5z = -41-4x + 1y - 5z = -41
~~~~
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x-5y-5z=-850x-5y-5z=-850x-5y-5z=-850x-5y-5z=-85
0x + 9y + 3z = 990x + 9y + 3z = 990x + 9y + 3z = 990x + 9y + 3z = 99
Passo 4:(-1/5)L2->L2,(1/3)L3->L3Passo 4:(-1/5)L2->L2,(1/3)L3->L3Passo 4:(-1/5)L2->L2,(1/3)L3->L3Passo 4:(-1/5)L2->L2,(1/3)L3->L3
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x - 5y - 5z = -850x - 5y - 5z = -850x - 5y - 5z = -850x - 5y - 5z = -85
0x + 9y + 3z = 990x + 9y + 3z = 990x + 9y + 3z = 990x + 9y + 3z = 99
~~~~
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x + 1y + 1z = 170x + 1y + 1z = 170x + 1y + 1z = 170x + 1y + 1z = 17
0x + 3y + 1z = 330x + 3y + 1z = 330x + 3y + 1z = 330x + 3y + 1z = 33
Passo 5: L3-3.L2->L3Passo 5: L3-3.L2->L3Passo 5: L3-3.L2->L3Passo 5: L3-3.L2->L3
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x + 1y + 1z = 170x + 1y + 1z = 170x + 1y + 1z = 170x + 1y + 1z = 17
0x + 3y + 1z = 330x + 3y + 1z = 330x + 3y + 1z = 330x + 3y + 1z = 33
~~~~
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x+1y+1z=170x+1y+1z=170x+1y+1z=170x+1y+1z=17
0x + 0y - 2z = -180x + 0y - 2z = -180x + 0y - 2z = -180x + 0y - 2z = -18
Passo 6: (-1/2)L3->L3Passo 6: (-1/2)L3->L3Passo 6: (-1/2)L3->L3Passo 6: (-1/2)L3->L3
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x+1y+1z=170x+1y+1z=170x+1y+1z=170x+1y+1z=17
~~~~
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x+1y+1z=170x+1y+1z=170x+1y+1z=170x+1y+1z=17

0x + 0y - 2z = -180x + 0y - 2z = -180x + 0y - 2z = -180x + 0y - 2z = -18 0x + 0y + 1z = 90x + 0y + 1z = 90x + 0y + 1z = 90x + 0y + 1z = 9
Passo 7: L2-L3->L2Passo 7: L2-L3->L2Passo 7: L2-L3->L2Passo 7: L2-L3->L2
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x + 1y + 1z = 170x + 1y + 1z = 170x + 1y + 1z = 170x + 1y + 1z = 17
0x + 0y + 1z = 90x + 0y + 1z = 90x + 0y + 1z = 90x + 0y + 1z = 9
~~~~
1x+2y+2z=351x+2y+2z=351x+2y+2z=351x+2y+2z=35
0x + 1y + 0z = 80x + 1y + 0z = 80x + 1y + 0z = 80x + 1y + 0z = 8
0x+0y+1z=90x+0y+1z=90x+0y+1z=90x+0y+1z=9
Passo 8: L1-2.L2-2.L3->L1Passo 8: L1-2.L2-2.L3->L1Passo 8: L1-2.L2-2.L3->L1Passo 8: L1-2.L2-2.L3->L1
1x + 2y + 2z = 351x + 2y + 2z = 351x + 2y + 2z = 351x + 2y + 2z = 35
0x + 1y + 0z = 80x + 1y + 0z = 80x + 1y + 0z = 80x + 1y + 0z = 8
0x + 0y + 1z = 90x + 0y + 1z = 90x + 0y + 1z = 90x + 0y + 1z = 9
~~~~
1x + 0y + 0z = 11x + 0y + 0z = 11x + 0y + 0z = 11x + 0y + 0z = 1
0x+1y+0z=80x+1y+0z=80x+1y+0z=80x+1y+0z=8
0x+0y+1z=90x+0y+1z=90x+0y+1z=90x+0y+1z=9
Passo 9: Simplificar coeficientesPasso 9: Simplificar coeficientesPasso 9: Simplificar coeficientesPasso 9: Simplificar coeficientes
1x + 0y + 0z = 11x + 0y + 0z = 11x + 0y + 0z = 11x + 0y + 0z = 1
0x + 1y + 0z = 80x + 1y + 0z = 80x + 1y + 0z = 80x + 1y + 0z = 8
0x + 0y + 1z = 90x + 0y + 1z = 90x + 0y + 1z = 90x + 0y + 1z = 9
~~~~
x = 1x = 1x = 1x = 1
y = 8y = 8y = 8y = 8
z = 9z = 9z = 9z = 9
Após o escalonamento, observamos que a solução obtida é exatamente fornecida pelo último sistema.
Sistemas lineares homogêneos
Um sistema linear é homogêneo quando os termos independentes de todas as equações são nulos. Todo
sistema linear homogêneo admite pelo menos a solução trivial, que é a solução identicamente nula. Assim,
todo sistema linear homogêneo é possível. Este tipo de sistema poderá ser determinado se admitir somente a
solução trivial ou indeterminado se admitir outras soluções além da trivial.
Exemplo: O sistema
2x - y + 3z = 0
4x + 2y - z = 0
x - y + 2z = 0
é determinado, pois possui a solução x=0, y=0 e z=0.
Regra de Cramer
Esta regra depende basicamente sobre o uso de determinantes. Para indicar o determinante de uma matriz
X, escreveremos det(X).
Seja um sistema linear com n equações e n incógnitas:
a11 x1 + a12 x2 +...+ a1j xj +...+ a1n xn = b1
a21 x1 + a22 x2 +...+ a2j xj +...+ a2n xn = b2
... ... ... ...
an1 xn + an2 xn +...+ anj xj +...+ ann xn = bn
A este sistema podemos associar algumas matrizes:

 Matriz dos coeficientes: Formada pelos coeficientes das incógnitas do sistema, aqui indicada pela
letra A.
Matriz dos coeficientesMatriz dos coeficientesMatriz dos coeficientesMatriz dos coeficientes
a11 a12 ... a1j ... a1na11 a12 ... a1j ... a1na11 a12 ... a1j ... a1na11 a12 ... a1j ... a1n
a21 a22 ... a2j ... a2na21 a22 ... a2j ... a2na21 a22 ... a2j ... a2na21 a22 ... a2j ... a2n
............ ............ ............ ............ ............ ............
an1 an2 ... anj ... annan1 an2 ... anj ... annan1 an2 ... anj ... annan1 an2 ... anj ... ann
 Matriz Aumentada do sistema: Formada todos os coeficientes das incógnitas do sistema e também
pelos termos independentes.
Matriz AumentadaMatriz AumentadaMatriz AumentadaMatriz Aumentada
a11 a12 ... a1j ... a1n b1a11 a12 ... a1j ... a1n b1a11 a12 ... a1j ... a1n b1a11 a12 ... a1j ... a1n b1
a21 a22 ... a2j ... a2n b2a21 a22 ... a2j ... a2n b2a21 a22 ... a2j ... a2n b2a21 a22 ... a2j ... a2n b2
............ ............ ............ ............ ............ ............
an1 an2 ... anj ... annan1 an2 ... anj ... annan1 an2 ... anj ... annan1 an2 ... anj ... ann
bnbnbnbn
 Matriz da incógnita xj: É a matriz Aj obtida ao substituirmos a coluna j (1<j<n) da matriz A, pelos
termos independentes das equações do sistema.
Matriz da incógnita xjMatriz da incógnita xjMatriz da incógnita xjMatriz da incógnita xj
a11 a12 ... b1 ... a1na11 a12 ... b1 ... a1na11 a12 ... b1 ... a1na11 a12 ... b1 ... a1n
a21 a22 ... b2 ... a2na21 a22 ... b2 ... a2na21 a22 ... b2 ... a2na21 a22 ... b2 ... a2n
............ ............ ............ ............ ............ ............
an1 an2 ... bn ... annan1 an2 ... bn ... annan1 an2 ... bn ... annan1 an2 ... bn ... ann
Quando as posições j=1,2,3 estão relacionadas com x1, x2 e x3 e substituídas pelas incógnitas x, y e z, é
comum escrever Ax, Ay e Az.
Se det(A) é diferente de zero, é possível obter cada solução xj (j=1,...,n), dividindo det(Aj) por det(A), isto é:
xj = det(Aj) / det(A)
Se det(A)=0, o sistema ainda poderá ser consistente, se todos os determinantes nxn da matriz aumentada do
sistema forem iguais a zero.
Um sistema impossível: Seja o sistema
2x + 3y + 4z = 27
1x - 2y + 3z = 15
3x + 1y + 7z = 40
A matriz A e a matriz aumentada Au do sistema estão mostradas abaixo.
2222 3333 4444
1111 -2-2-2-2 3333
3333 1111 7777
2222 3333 4444 27272727
1111 -2-2-2-2 3333 15151515

3333 1111 7777 40404040
Como det(A)=0, devemos verificar se todos os determinantes das sub-matrizes 3×3 da matriz aumentada são
nulos. Se existir pelo menos um deles não nulo, o sistema será impossível e este é o caso pois é não nulo o
determinante da sub-matriz 3x3 formada pelas colunas 1, 2 e 4 da matriz aumentada:
2222 3333 27272727
1111 -2-2-2-2 15151515
3333 1111 40404040
Um sistema indeterminado: Consideremos agora o sistema (Quase igual ao anterior: trocamos 40 por 42 na
última linha!)
2x + 3y + 4z = 27
1x - 2y + 3z = 15
3x + 1y + 7z = 42
A matriz A e a matriz aumentada Au do sistema, estão abaixo:
2222 3333 4444
1111 -2-2-2-2 3333
3333 1111 7777
2222 3333 4444 27272727
1111 -2-2-2-2 3333 15151515
3333 1111 7777 42424242
Aqui, tanto det(A)=0 como todos os determinantes das sub-matrizes 3×3 da matriz aumentada são nulos,
então o sistema é possível e indeterminado. Neste caso, observamos que a última linha é a soma das duas
primeiras e como estas duas primeiras dependem de x, y e z, você poderá encontrar as soluções, por
exemplo, de x e y em função de z.
Um sistema com solução única: Seja o sistema
2x + 3y + 4z = 27
1x - 2y + 3z = 15
3x + 1y + 6z = 40
A matriz A e a matriz dos termos independentes do sistema estão indicados abaixo.
2222 3333 4444
1111 -2-2-2-2 3333
3333 1111 6666
27272727
15151515
40404040

Como det(A)=7, o sistema admite uma única solução que depende dos determinantes das matrizes Ax, Ay e
Az, e tais matrizes são obtidas pela substituição 1a., 2a. e 3a. colunas da matriz A pelos termos
independentes das três equações, temos:
Ax=Ax=Ax=Ax=
27272727 3333 4444
15151515 -2-2-2-2 3333
40404040 1111 6666
Ay=Ay=Ay=Ay=
2222 27272727 4444
1111 15151515 3333
3333 40404040 6666
Az=Az=Az=Az=
2222 3333 27272727
1111 -2-2-2-2 15151515
3333 1111 40404040
Como det(Ax)=65, det(Ay)=1 e det(Az)=14, a solução do sistema é dada por:
x = det(Ax)/det(A) = 65/7
y = det(Ay)/det(A) = 1/7
z = det(Az)/det(A) = 14/7
Geometria plana: Áreas e perímetros.
Triângulo e região triangular
No desenho abaixo, o triângulo ABC é a reunião dos segmentos de reta AB, BC e AC. A reunião de todos os
pontos localizados no triângulo e também dentro do triângulo é chamada uma região triangular. A região
triangular ABC é limitada pelo triângulo ABC. Os pontos dos lados do triângulo ABC bem como os pontos
do interior do triângulo ABC são pontos da região triangular.
Triângulo ABCTriângulo ABCTriângulo ABCTriângulo ABC Região triangular ABCRegião triangular ABCRegião triangular ABCRegião triangular ABC
Duas ou mais regiões triangulares não são sobrepostas, se a interseção é vazia, é um ponto ou é um
segmento de reta. Cada uma das regiões planas abaixo é a reunião de três regiões triangulares não
sobrepostas.
O conceito de região poligonal
Uma região poligonal é a reunião de um número finito de regiões triangulares não-sobrepostas e coplanares
(estão no mesmo plano). Na gravura abaixo, apresentamos quatro regiões poligonais. Observe que uma
região triangular é por si mesmo uma região poligonal e além disso uma região poligonal pode conter

"buracos".
Uma região poligonal pode ser decomposta em várias regiões triangulares e isto pode ser feito de várias
maneiras
Duas ou mais regiões poligonais são não-sobrepostas quando a interseção de duas regiões quaisquer, é vazia,
é um conjunto finito de pontos, é um segmento de reta ou é um conjunto finito de pontos e um segmento
de reta.
O estudo de área de regiões poligonais depende de alguns conceitos primitivos:
1. A cada região poligonal corresponde um único número real positivo chamado área.
2. Se dois triângulos são congruentes então as regiões limitadas por eles possuem a mesma área.
3. Se uma região poligonal é a reunião de n regiões poligonais não-sobrepostas então sua área é a soma
das áreas das n-regiões.
Observação: Para facilitar o estudo de regiões poligonais, adotaremos as seguintes práticas:
a. Os desenhos de regiões poligonais serão sombreadas apenas quando houver possibilidade de
confusão entre o polígono e a região.
b. Usaremos expressões como a área do triângulo ABC e a área do retângulo RSTU no lugar de
expressões como a área da região triangular ABC e a área da região limitada pelo retângulo RSTU.
Exemplo: A área da figura poligonal ABCDEFX pode ser obtida pela decomposição da região poligonal em
regiões triangulares.
Após isto, realizamos as somas dessas áreas triangulares.
Área(ABCDEFX)=área(XAB)+área(XBC)+...+área(XEF)
Unidade de área
Para a unidade de medida de área, traçamos um quadrado cujo lado tem uma unidade de comprimento.
Esta unidade pode ser o metro, o centímetro, o quilômetro, etc.
Área do Retângulo
A figura ao lado mostra o retângulo ABCD, que mede 3 unidades de comprimento e 2 unidades de altura. O
segmento horizontal que passa no meio do retângulo e os segmentos verticais, dividem o retângulo em seis

quadrados tendo cada um 1 unidade de área.
A área do retângulo ABCD é a soma das áreas destes seis quadrados. O número de unidades de área do
retângulo coincide com o obtido pelo produto do número de unidades do comprimento da base AB pelo
número de unidades da altura BC.
O lado do retângulo pode ser visto como a base e o lado adjacente como a altura, assim, a área A do
retângulo é o produto da medida da base b pela medida da altura h.
A = b × h
Área do quadrado
Um quadrado é um caso particular de retângulo cuja medida da base é igual à medida da altura. A área do
quadrado pode ser obtida pelo produto da medida da base por si mesma.
Esta é a razão pela qual a segunda potência do número x, indicada por x², tem o nome de quadrado de x e a
área A do quadrado é obtida pelo quadrado da medida do lado x.
A = x²
Exemplo: Obter a área do retângulo cujo comprimento da base é 8 unidades e o comprimento da altura é 5
unidades.
A = b×h
A = (8u)x(5u) = 40u²
No cálculo de áreas em situações reais, usamos medidas de comprimento em função de alguma certa
unidade como: metro, centímetro, quilômetro, etc...
Exemplo: Para calcular a área de um retângulo com 2 m de altura e 120 cm de base, podemos expressar a
área em metros quadrados ou qualquer outra unidade de área.
1. Transformando as medidas em metros
Como h=2m e b=120cm=1,20m, a área será obtida através de:
A = b×h
A = (1,20m)×(2m) = 2,40m²
2. Transformando as medidas em centímetros
Como h=2m=200cm e b=120cm, a área do retângulo será dada por:
A = b×h
A = (120cm)×(200cm) = 24000cm²
Área do Paralelogramo
Combinando os processos para obtenção de áreas de triângulos congruentes com aqueles de áreas de
retângulos podemos obter a área do paralelogramo.

Qualquer lado do paralelogramo pode ser tomado como sua base e a altura correspondente é o segmento
perpendicular à reta que contém a base até o ponto onde esta reta intercepta o lado oposto do
paralelogramo.
No paralelogramo ABCD abaixo à esquerda, os segmentos verticais tracejados são congruentes e qualquer
um deles pode representar a altura do paralelogramo em relação à base AB.
No paralelogramo RSTV acima à direita, os dois segmentos tracejados são congruentes e qualquer um deles
pode representar a altura do paralelogramo em relação à base RV.
A área A do paralelogramo é obtida pelo produto da medida da base b pela medida da altura h, isto é,
A=b×h. Demonstração da fórmula
Área do Triângulo
A área de um triângulo é a metade do produto da medida da base pela medida da altura, isto é, A=b.h/2.
Demonstração da fórmula
Exemplo: Mostraremos que a área do triângulo equilátero cujo lado mede s é dada por A=s²R[3]/2, onde
R[z] denota a raiz quadrada de z>0. Realmente, com o Teorema de Pitágoras, escrevemos h²=s²-(s/2)² para
obter h²=(3/4)s² garantindo que h=R[3]s/2.
Como a área de um triângulo é dada por A=b.h/2, então segue que:
A = s × R[3] s/2 = ½ R[3] s²
Observação: Triângulos com bases congruentes e alturas congruentes possuem a mesma área.
Comparação de áreas entre triângulos semelhantes
Conhecendo-se a razão entre medidas correspondentes quaisquer de dois triângulos semelhantes, é possível
obter a razão entre as áreas desses triângulos.
Propriedade: A razão entre as áreas de dois triângulos semelhantes é igual ao quadrado da razão entre os
comprimentos de quaisquer dois lados correspondentes.
Área de ABCÁrea de ABCÁrea de ABCÁrea de ABC ==== a²a²a²a² ==== b²b²b²b² ==== c²c²c²c²

Área de RSTÁrea de RSTÁrea de RSTÁrea de RST r²r²r²r² s²s²s²s² t²t²t²t²
Área do losango
O losango é um paralelogramo e a sua área é também igual ao produto do comprimento da medida da base
pela medida da altura.
A área do losango é o semi-produto das medidas das diagonais, isto é, A=(d1×d2)/2. Demonstração da
fórmula
Área do trapézio
Em um trapézio existe uma base menor de medida b1, uma base maior de medida b2 e uma altura com
medida h.
A área A do trapézio é o produto da média aritmética entre as medidas das bases pela medida da altura, isto
é, A=(b1+b2).h/2.
Polígonos regulares
Um polígono regular é aquele que possui todos os lados congruentes e todos os ângulos congruentes.
Existem duas circunferências associadas a um polígono regular.
Circunferência circunscrita: Em um polígono regular com n lados, podemos construir uma circunferência
circunscrita (por fora), que é uma circunferência que passa em todos os vértices do polígono e que contém o
polígono em seu interior.
Circunferência inscrita: Em um polígono regular com n lados, podemos colocar uma circunferência inscrita
(por dentro), isto é, uma circunferência que passa tangenciando todos os lados do polígono e que está
contida no polígono.
Elementos de um polígono regular
1. Centro do polígono é o centro comum às circunferências inscrita e circunscrita.
2. Raio da circunferência circunscrita é a distância do centro do polígono até um dos vértices.

3. Raio da circunferência inscrita é o apótema do polígono, isto é, a distância do centro do polígono ao
ponto médio de um dos lados.
4. Ângulo central é o ângulo cujo vértice é o centro do polígono e cujos lados contém vértices
consecutivos do polígono.
Apótema: OM,Apótema: OM,Apótema: OM,Apótema: OM,
Raios: OA,OFRaios: OA,OFRaios: OA,OFRaios: OA,OF
Ângulo central: AOFÂngulo central: AOFÂngulo central: AOFÂngulo central: AOF
Apótema: OX,Apótema: OX,Apótema: OX,Apótema: OX,
Raios: OR,OTRaios: OR,OTRaios: OR,OTRaios: OR,OT
Ângulo central: ROTÂngulo central: ROTÂngulo central: ROTÂngulo central: ROT
5. Medida do ângulo central de um polígono com n lados é dada por 360/n graus. Por exemplo, o
ângulo central de um hexágono regular mede 60 graus e o ângulo central de um pentágono regular
mede 360/5=72 graus.
Áreas de polígonos regulares
Traçando segmentos de reta ligando o centro do polígono regular a cada um dos vértices desse polígono de
n-lados, iremos decompor este polígono em n triângulos congruentes.
Assim, a fórmula para o cálculo da área da região poligonal regular será dada pela metade do produto da
medida do apótema a pelo perímetro P, isto é:
A = a × Perímetro / 2
Demonstração da fórmula
Comparando áreas entre polígonos semelhantes
Apresentamos abaixo dois pentágonos irregulares semelhantes. Dos vértices correspondentes A e L
traçamos diagonais decompondo cada pentágono em três triângulos.
Os pares de triângulos correspondentes ABC e LMN, parecem semelhantes, o que pode ser verificado
diretamente através da medição de seus ângulos com um transferidor. Assumiremos que tal propriedade seja
válida para polígonos semelhantes com n lados.
Observação: Se dois polígonos são semelhantes, eles podem ser decompostos no mesmo número de
triângulos e cada triângulo é semelhante ao triângulo que ocupa a posição correspondente no outro

polígono.
Este fato e o teorema sobre razão entre áreas de triângulos semelhantes são usados para demonstrar o
seguinte teorema sobre áreas de polígonos semelhantes.
Teorema: A razão entre áreas de dois polígonos semelhantes é igual ao quadrado da razão entre os
comprimentos de quaisquer dois lados correspondentes.
Área de ABCDE...Área de ABCDE...Área de ABCDE...Área de ABCDE...
Área de A'B'C'D'E'...Área de A'B'C'D'E'...Área de A'B'C'D'E'...Área de A'B'C'D'E'...
====
s²s²s²s²
(s')²(s')²(s')²(s')²
====
t²t²t²t²
(t')²(t')²(t')²(t')²
O círculo como o limite de regiões poligonais regulares
Nas figuras abaixo, temos três regiões poligonais regulares inscritas em círculos congruentes.
Quando aumenta o número de lados do polígono inscrito observamos que també aumenta:
1. O apótema, aproximando-se do raio do cículo como um limite.
2. O perímetro, aproximando-se da circunferência do círculo como um limite.
3. A área, aproximando-se da área do círculo como um limite.
Neste trabalho não é possível apresentar uma definição precisa de limite e sem ela não podemos construir
uma expressão matemática para o cálculo do perímetro ou da área de uma região poligonal regular inscrita
num círculo.
A idéia de limite nos permite aproximar o perímetro da circunferência pelo perímetro do polígono regular
inscrito nessa circunferência, à medida que o número de lados do polígono aumenta.
O mesmo ocorre com o cálculo da área do círculo, pois à medida que o número de lados da região poligonal
inscrita aumenta, as áreas dessas regiões se aproximam da área do círculo. Este também é um processo
através de limites.
Perímetro do círculo e da circunferência
Perímetro da circunferência de um círculo é o valor limite da sequência dos perímetros dos polígonos

regulares inscritos de n lados na circunferência à medida que o número n de lados aumenta
indefinidamente.
Área do círculo é o valor limite da sequência das áreas das regiões poligonais regulares inscritas no círculo
quando o número n de lados das poligonais aumenta arbitrariamente.
Relações associadas ao perímetro
1. Com base nestas duas definições temos um importante resultado sobre a relação existente entre o
perímetro e o diâmetro da circunferência:
A razão entre o perímetro e o diâmetro
de uma circunferência é uma constante
2. Sejam duas circunferências de diâmetros D1 e D2, com perímetros P1 e P2, respectivamente. A razão
entre os perímetros P1 e P2 é igual à razão entre os diâmetros D1 e D2. Como o diâmetro é o dobro
do raio, então, o mesmo ocorre para a razão entre os raios r1 e r2.
A1A1A1A1
A2A2A2A2
====
D1D1D1D1
D2D2D2D2
====
r1r1r1r1
r2r2r2r2
3. Para todo círculo (e também circunferência), a razão entre o perímetro e o diâmetro é uma
constante, denominada Pi, denotada pela letra grega que é um número irracional (não
pode ser escrito como a divisão de dois números inteiros). Uma aproximação para Pi com 10 dígitos
decimais é:
= 3,1415926536....
Área do círculo
Área de um círculo de raio r é o limite das áreas das regiões poligonais regulares inscritas no mesmo. Nesse
caso, o diâmetro D=2r. As fórmulas para a área do círculo são:
Área = r² = ¼ D²
Proporção com áreas: Sejam dois círculos de raios, respectivamente, iguais a r1 e r2, áreas A1 e A2 e
diâmetros D1 e D2. A razão entre as áreas desses dois círculos é a mesma que a razão entre os quadrados de
seus raios ou os quadrados de seus diâmetros.
A1A1A1A1
====
(D1)²(D1)²(D1)²(D1)²
====
(r1)²(r1)²(r1)²(r1)²

A2A2A2A2 (D2)²(D2)²(D2)²(D2)² (r2)²(r2)²(r2)²(r2)²
Arcos
O comprimento de um arco genérico AB pode ser descrito em termos de um limite. Imaginemos o arco AB
contendo vários pontos A=Po, P1, P2, P3, ..., Pn-1, Pn=B, formando n pequenos arcos e também n pequenos
segmentos de reta de medidas respectivas iguais a: AP1, P1P2, ..., Pn-1B.
A idéia aqui é tomar um número n bastante grande para que cada segmento seja pequeno e as medidas dos
arcos sejam aproximadamente iguais às medidas dos segmentos.
O comprimento de um arco AB de uma circunferência de raio r é o valor limite da soma dos comprimentos
destas n cordas quando n cresce indefinidamente.
Um arco completo de circunferência corresponde a um ângulo que mede 360 graus=2 radianos.
Se o raio da circunferência for r, o perímetro da circunferência coincidirá com o comprimento do arco da
mesma e é dado por:
Perímetro da circunferência = 2 r
Comprimento do arco: Seja um arco AB em uma circunferência de raio r e m a medida do
ângulo correspondente, sendo m tomado em graus ou em radianos. O comprimento do
arco pode ser obtido (em radianos) por:
Comprimento do arco AB = r m/180 = r m
Tais fórmulas podem ser justificadas pelas seguintes regras de três simples e diretas.
Se o ângulo relativo ao arco AB mede m graus, obtemos:
360 graus ……… 2 Pi r
m graus ……… Comprimento de AB
logo
comprimento do arco AB = m r / 180
Se o ângulo relativo ao arco AB mede m radianos, obtemos:
2 Pi rad ……… 2 Pi r
m rad ……… comprimento de AB
assim
Comprimento do arco AB = r m radianos

Setor circular
Setor circular é uma região limitada por dois raios e um arco do círculo.
Usando a figura acima, podemos extrair algumas informações:
1. OACB é um setor circular
2. OADB é um setor circular
3. r é o raio de cada um dos setores
4. ACB é o arco do setor OACB
5. ADB é o arco do setor OADB.
6. Tomando m como a medida do arco ACB (em graus ou radianos), a área do setor circular OACB será
dada por:
Área do setor circular OACB = r² m/360 = ½ m r²
Basta usar regras de três simples e diretas. Se o ângulo relativo ao arco AB mede m graus, obtemos:
360 graus ……… Área do círculo
m graus ……… Área do setor OACB
logo
Área(setor OACB) = Pi r² m / 360
Se o ângulo relativo ao arco AB mede m radianos, obtemos:
2 Pi rad ……… Área do círculo
m rad ……… Área setor OACB
assim
Área(setor OACB) = ½ m r² radianos
Segmento circular
Segmento circular é uma região limitada por uma corda e um arco do círculo. Na figura abaixo, existem dois
segmentos circulares: o segmento ACB e o segmento ADB.
A área do segmento ACB pode ser obtida subtraindo a área do triângulo AOB da área do setor OACB.
Área(segmento) = Área(setor OACB) - Área(triângulo AOB)
A área do segmento ADB pode ser obtida subtraindo a área do segmento ACB da área do círculo ou
somando a área do triângulo AOB à área do setor OADB.

Curiosidades sobre o número Pi
1. Na Bíblia Sagrada, no primeiro livro de Reis 7:23, existe a passagem:
"Fez também o mar de fundição; era redondo
e media dez côvados duma borda à outra, cinco
côvados de altura e trinta de circunferência."
sugerindo que os construtores da casa de Salomão usavam o valor 3 para a razão entre o diâmetro e o
comprimento da circunferência.
2. Arquimedes (287-212 a.C.) mostrou que o valor da razão entre o diâmetro e o comprimento da
circunferência estava entre 3+1/7 e 3+10/71.
3. O símbolo usado para a razão entre o diâmetro e o comprimento da circunferência
somente foi introduzido no século XVIII.
4. O valor de correto com 10 dígitos decimais foi usado no cálculo do comprimento da
linha do Equador terrestre.
5. Uma vez conhecida uma unidade de comprimento, é impossível construir um segmento de
comprimento Pi através de régua e compasso.
6. O número exerce um papel muito importante na Matemática e nas ciências,
predominantemente quando determinamos perímetros, áreas, centros de gravidade, informações
sobre segmentos e setores circulares e elípticos, inclusive em cálculos de navegação, etc.
7. Com o uso de computadores, já foi realizado o cálculo do valor exato de com mais de
cem mil dígitos decimais.
Detalhes sobre o cálculo de Pi: De modo análogo ao resultado obtido através do limite de polígonos
regulares inscritos também podemos aproximar o perímetro e a área do círculo de raio r, pelo valor limite
de polígonos regulares circunscritos no círculo quando o número de lados desse cresce arbitrariamente.
Perímetro polígono inscritoPerímetro polígono inscritoPerímetro polígono inscritoPerímetro polígono inscrito
2r2r2r2r
<<<< <<<<
Perímetro polígono circunscritoPerímetro polígono circunscritoPerímetro polígono circunscritoPerímetro polígono circunscrito
2r2r2r2r
Tais relações estão na tabela com dados sobre o polígono regular dado:
Número de ladosNúmero de ladosNúmero de ladosNúmero de lados
do polígonodo polígonodo polígonodo polígono
Perímetro do polígonoPerímetro do polígonoPerímetro do polígonoPerímetro do polígono
inscrito dividido por 2rinscrito dividido por 2rinscrito dividido por 2rinscrito dividido por 2r
Perímetro do polígonoPerímetro do polígonoPerímetro do polígonoPerímetro do polígono
circunscrito dividido por 2rcircunscrito dividido por 2rcircunscrito dividido por 2rcircunscrito dividido por 2r

6666 3,000003,000003,000003,00000 3,464113,464113,464113,46411
12121212 3,105823,105823,105823,10582 3,215403,215403,215403,21540
24242424 3,132623,132623,132623,13262 3,159673,159673,159673,15967
48484848 3,139353,139353,139353,13935 3,146093,146093,146093,14609
96969696 3,141033,141033,141033,14103 3,142723,142723,142723,14272
192192192192 3,141453,141453,141453,14145 3,141883,141883,141883,14188
256256256256 3,141513,141513,141513,14151 3,141753,141753,141753,14175
512512512512 3,141573,141573,141573,14157 3,141633,141633,141633,14163
1024102410241024 3,141593,141593,141593,14159 3,141603,141603,141603,14160
Observe na tabela que quanto maior o número de lados de cada polígono mais dígitos decimais coincidem
para obter o valor do número Pi, tanto para os polígonos inscritos como para os circunscritos. Com um
polígono de 1024 lados, praticamente temos 4 algarismos exatos.
Outra forma (lenta) para obter o número Pi, é:
A forma mais rápida que conhecemos para obter Pi, é:
Geometria espacial: áreas e volumes.
Volume de um "cilindro"
Em um cilindro, o volume é dado pelo produto da área da base pela altura.
V = A(base) h
Se a base é um círculo de raio r, e pi=3,141593..., então:
V = pi r² h
Exercício: Calcular o volume de um cilindro oblíquo com base elíptica (semi-eixos a e b) e altura h.
Área lateral e área total de um cilindro circular reto

Em um cilindro circular reto, a área lateral é dada por A(lateral)=2pi.r.h, onde r é o raio da base e h é a
altura do cilindro. A área total corresponde à soma da área lateral com o dobro da área da base.
A(total) = A(lateral) + 2 A(base)A(total) = A(lateral) + 2 A(base)A(total) = A(lateral) + 2 A(base)A(total) = A(lateral) + 2 A(base)
A(total) = 2 pi r h + 2 pi r²A(total) = 2 pi r h + 2 pi r²A(total) = 2 pi r h + 2 pi r²A(total) = 2 pi r h + 2 pi r²
A(total) = 2 pi r(h+r)A(total) = 2 pi r(h+r)A(total) = 2 pi r(h+r)A(total) = 2 pi r(h+r)
Exemplo: Um cilindro circular equilátero é aquele cuja altura é igual ao diâmetro da base, isto é h=2r. Neste
caso, para calcular a área lateral, a área total e o volume, podemos usar as fórmulas, dadas por:
A(lateral) = 4 pi r²A(lateral) = 4 pi r²A(lateral) = 4 pi r²A(lateral) = 4 pi r²
A(base) = pi r²A(base) = pi r²A(base) = pi r²A(base) = pi r²
A(total) = A(lateral) + 2 A(base) = 6 pi r²A(total) = A(lateral) + 2 A(base) = 6 pi r²A(total) = A(lateral) + 2 A(base) = 6 pi r²A(total) = A(lateral) + 2 A(base) = 6 pi r²
Volume = A(base).h = pi r².2r = 2 pi r³Volume = A(base).h = pi r².2r = 2 pi r³Volume = A(base).h = pi r².2r = 2 pi r³Volume = A(base).h = pi r².2r = 2 pi r³
Exercício: Seja um cilindro circular reto de raio igual a 2cm e altura 3cm. Calcular a área lateral, área total e
o seu volume.
A(base) = pi.r² = pi.2² = 4 pi cm²
A(lateral) = 2.pi.r.h = 2.pi.2.3 = 12 pi cm²
A(total) = A(lateral) + 2 A(base) = 12pi + 8pi = 20 pi cm²
Volume = A(base).h = pi.r²h = pi.4.3 = 12 pi cm³
A esfera no espaço R³ é uma superfície muito importante em função de suas aplicações a problemas da vida.
Do ponto de vista matemático, a esfera no espaço R³ é confundida com o sólido geométrico (disco esférico)
envolvido pela mesma, razão pela qual muitas pessoas calculam o volume da esfera. Na maioria dos livros
elementares sobre Geometria, a esfera é tratada como se fosse um sólido, herança da Geometria Euclidiana.
Embora não seja correto, muitas vezes necessitamos falar palavras que sejam entendidas pela coletividade.
De um ponto de vista mais cuidadoso, a esfera no espaço R³ é um objeto matemático parametrizado por
duas dimensões, o que significa que podemos obter medidas de área e de comprimento mas o volume tem
medida nula. Há outras esferas, cada uma definida no seu respectivo espaço n-dimensional. Um caso
interessante é a esfera na reta unidimensional:
So = {x em R: x²=1} = {+1,-1}
Por exemplo, a esfera

S1 = { (x,y) em R²: x² + y² = 1 }
é conhecida por nós como uma circunferência de raio unitário centrada na origem do plano cartesiano.
Aplicação: volumes de líquidos
Um problema fundamental para empresas que armazenam líquidos em tanques esféricos, cilíndricos ou
esféricos e cilíndricos é a necessidade de realizar cálculos de volumes de regiões esféricas a partir do
conhecimento da altura do líquido colocado na mesma. Por exemplo, quando um tanque é esférico, ele
possui um orifício na parte superior (polo Norte) por onde é introduzida verticalmente uma vara com
indicadores de medidas. Ao retirar a vara, observa-se o nível de líquido que fica impregnado na vara e esta
medida corresponde à altura de líquido contido na região esférica. Este não é um problema trivial, como
observaremos pelos cálculos realizados na sequência.
A seguir apresentaremos elementos esféricos básicos e algumas fórmulas para cálculos de áreas na esfera e
volumes em um sólido esférico.
A superfície esférica
A esfera no espaço R³ é o conjunto de todos os pontos do espaço que estão localizados a uma mesma
distância denominada raio de um ponto fixo chamado centro.
Uma notação para a esfera com raio unitário centrada na origem de R³ é:
S² = { (x,y,z) em R³: x² + y² + z² = 1 }
Uma esfera de raio unitário centrada na origem de R4 é dada por:
S³ = { (w,x,y,z) em R4: w² + x² + y² + z² = 1 }
Você conseguiria imaginar espacialmente tal esfera?
Do ponto de vista prático, a esfera pode ser pensada como a película fina que envolve um sólido esférico.
Em uma melancia esférica, a esfera poderia ser considerada a película verde (casca) que envolve a fruta.
É comum encontrarmos na literatura básica a definição de esfera como sendo o sólido esférico, no entanto
não se deve confundir estes conceitos. Se houver interesse em aprofundar os estudos desses detalhes, deve-
se tomar algum bom livro de Geometria Diferencial que é a área da Matemática que trata do detalhamento
de tais situações.
O disco esférico é o conjunto de todos os pontos do espaço que estão localizados na casca e dentro da esfera.
Do ponto de vista prático, o disco esférico pode ser pensado como a reunião da película fina que envolve o
sólido esférico com a região sólida dentro da esfera. Em uma melancia esférica, o disco esférico pode ser
visto como toda a fruta.

Quando indicamos o raio da esfera pela letra R e o centro da esfera pelo ponto (0,0,0), a equação da esfera é
dada por:
x² + y² + z² = R²
e a relação matemática que define o disco esférico é o conjunto que contém a casca reunido com o interior,
isto é:
x² + y² + z² < R²
Quando indicamos o raio da esfera pela letra R e o centro da esfera pelo ponto (xo,yo,zo), a equação da
esfera é dada por:
(x-xo)² + (y-yo)² + (z-zo)² = R²
e a relação matemática que define o disco esférico é o conjunto que contém a casca reunido com o interior,
isto é, o conjunto de todos os pontos (x,y,z) em R³ tal que:
(x-xo)² + (y-yo)² + (z-zo)² < R²
Da forma como está definida, a esfera centrada na origem pode ser construída no espaço euclidiano R³ de
modo que o centro da mesma venha a coincidir com a origem do sistema cartesiano R³, logo podemos fazer
passar os eixos OX, OY e OZ, pelo ponto (0,0,0).
Seccionando a esfera x²+y²+z²=R² com o plano z=0, obteremos duas superfícies semelhantes: o hemisfério
Norte ("boca para baixo") que é o conjunto de todos os pontos da esfera onde a cota z é não negativa e o
hemisfério Sul ("boca para cima") que é o conjunto de todos os pontos da esfera onde a cota z não é positiva.
Se seccionarmos a esfera x²+y²+z²=R² por um plano vertical que passa em (0,0,0), por exemplo, o plano x=0,
teremos uma circunferência maximal C da esfera que é uma circunferência contida na esfera cuja medida
do raio coincide com a medida do raio da esfera, construída no plano YZ e a equação desta circunferência
será:
x=0, y² + z² = R2
sendo que esta circunferência intersecta o eixo OZ nos pontos de coordenadas (0,0,R) e (0,0,-R). Existem
infinitas circunferências maximais em uma esfera.
Se rodarmos esta circunferência maximal C em torno do eixo OZ, obteremos a esfera através da rotação e
por este motivo, a esfera é uma superfície de revolução.
Se tomarmos um arco contido na circunferência maximal cujas extremidades são os pontos (0,0,R) e (0,p,q)
tal que p²+q²=R² e rodarmos este arco em torno do eixo OZ, obteremos uma superfície denominada calota
esférica.
Na prática, as pessoas usam o termo calota esférica para representar tanto a superfície como o sólido
geométrico envolvido pela calota esférica. Para evitar confusões, usarei "calota esférica" com aspas para o
sólido e sem aspas para a superfície.

A partir da rotação, construiremos duas calotas em uma esfera, de modo que as extremidades dos arcos
sejam (0,0,R) e (0,p,q) com p²+q²=R² no primeiro caso (calota Norte) e no segundo caso (calota Sul) as
extremidades dos arcos (0,0,-R) e (0,r,-s) com r²+s²=R² e retirarmos estas duas calotas da esfera, teremos
uma superfície de revolução denominada zona esférica.
De um ponto de vista prático, consideremos uma melancia esférica. Com uma faca, cortamos uma "calota
esférica" superior e uma "calota esférica" inferior. O que sobra da melancia é uma região sólida envolvida
pela zona esférica, algumas vezes denominada zona esférica.
Consideremos uma "calota esférica" com altura h1 e raio da base r1 e retiremos desta calota uma outra
"calota esférica" com altura h2 e raio da base r2, de tal modo que os planos das bases de ambas sejam
paralelos. A região sólida determinada pela calota maior menos a calota menor recebe o nome de segmento
esférico com bases paralelas.
No que segue, usaremos esfera tanto para o sólido como para a superfície, "calota esférica" para o sólido
envolvido pela calota esférica, a letra maiúscula R para entender o raio da esfera sobre a qual estamos
realizando os cálculos, V será o volume, A(lateral) será a área lateral e e A(total) será a área total.
Algumas fórmulas (relações) para objetos esféricos
ObjetoObjetoObjetoObjeto Relações e fórmulasRelações e fórmulasRelações e fórmulasRelações e fórmulas
EsferaEsferaEsferaEsfera
Volume = (4/3) Pi R³Volume = (4/3) Pi R³Volume = (4/3) Pi R³Volume = (4/3) Pi R³
A(total) = 4 Pi R²A(total) = 4 Pi R²A(total) = 4 Pi R²A(total) = 4 Pi R²
Calota esféricaCalota esféricaCalota esféricaCalota esférica
(altura h, raio da base r)(altura h, raio da base r)(altura h, raio da base r)(altura h, raio da base r)
R² = h (2R-h)R² = h (2R-h)R² = h (2R-h)R² = h (2R-h)
A(lateral) = 2 Pi R hA(lateral) = 2 Pi R hA(lateral) = 2 Pi R hA(lateral) = 2 Pi R h
A(total) = Pi h (4R-h)A(total) = Pi h (4R-h)A(total) = Pi h (4R-h)A(total) = Pi h (4R-h)
V=Pi.h²(3R-h)/3=Pi(3R²+h²)/6V=Pi.h²(3R-h)/3=Pi(3R²+h²)/6V=Pi.h²(3R-h)/3=Pi(3R²+h²)/6V=Pi.h²(3R-h)/3=Pi(3R²+h²)/6
Segmento esféricoSegmento esféricoSegmento esféricoSegmento esférico
(altura h, raios das bases r1>r²)(altura h, raios das bases r1>r²)(altura h, raios das bases r1>r²)(altura h, raios das bases r1>r²)
R² = a² + [(r1² -r2²-h²)/2h)]²R² = a² + [(r1² -r2²-h²)/2h)]²R² = a² + [(r1² -r2²-h²)/2h)]²R² = a² + [(r1² -r2²-h²)/2h)]²
A(lateral) = 2 Pi R hA(lateral) = 2 Pi R hA(lateral) = 2 Pi R hA(lateral) = 2 Pi R h
A(total) = Pi(2Rh+r1²+r2²)A(total) = Pi(2Rh+r1²+r2²)A(total) = Pi(2Rh+r1²+r2²)A(total) = Pi(2Rh+r1²+r2²)
Volume=Pi.h(3r1²+3r2²+h²)/6Volume=Pi.h(3r1²+3r2²+h²)/6Volume=Pi.h(3r1²+3r2²+h²)/6Volume=Pi.h(3r1²+3r2²+h²)/6
Estas fórmulas podem ser obtidas como aplicações do Cálculo Diferencial e Integral, mas nós nos
limitaremos a apresentar um processo matemático para a obtenção da fórmula do cálculo do volume da
"calota esférica" em função da altura da mesma.
Volume de uma calota no hemisfério Sul
Consideremos a esfera centrada no ponto (0,0,R) com raio R.
A equação desta esfera será dada por:

x² + y² + (z-R)² = R²
A altura da calota será indicada pela letra h e o plano que coincide com o nível do líquido (cota) será
indicado por z=h. A interseção entre a esfera e este plano é dado pela circunferência
x² + y² = R² - (h-R)²
Obteremos o volume da calota esférica com a altura h menor ou igual ao raio R da esfera, isto é, h pertence
ao intervalo [0,R] e neste caso poderemos explicitar o valor de z em função de x e y para obter:
Para simplificar as operações algébricas, usaremos a letra r para indicar:
r² = R² - (h-R)² = h(2R-h)
A região circular S de integração será descrita por x²+y²<R² ou em coordenadas polares através de:
0<m<R, 0<t<2Pi
A integral dupla que representa o volume da calota em função da altura h é dada por:
ou seja
Escrita em Coordenadas Polares, esta integral fica na forma:
Após realizar a integral na variável t, podemos separá-la em duas integrais:
ou seja:
Com a mudança de variável u=R²-m² e du=(-2m)dm poderemos reescrever:
Após alguns cálculos obtemos:
VC(h) = Pi (h-R) [R² -(h-R)²] - (2/3)Pi[(R-h)³ - R³]
e assim temos a fórmula para o cálculo do volume da calota esférica no hemisfério Sul com a altura h no
intervalo [0,R], dada por:
VC(h) = Pi h²(3R-h)/3
Volume de uma calota no hemisfério Norte

Se o nível do líquido mostra que a altura h já ultrapassou o raio R da região esférica, então a altura h está no
intervalo [R,2R]
Lançaremos mão de uma propriedades de simetria da esfera que nos diz que o volume da calota superior
assim como da calota inferior somente depende do raio R da esfera e da altura h e não da posição relativa
ocupada.
Aproveitaremos o resultado do cálculo utilizado para a calota do hemisfério Sul. Tomaremos a altura tal
que: h=2R-d, onde d é a altura da região que não contém o líquido. Como o volume desta calota vazia é
dado por:
VC(d) = Pi d²(3R-d)/3
e como h=2R-d, então para h no intervalo [R,2R], poderemos escrever o volume da calota vazia em função
de h:
VC(h) = Pi (2R-h)²(R+h)/3
Para obter o volume ocupado pelo líquido, em função da altura, basta tomar o volume total da região
esférica e retirar o volume da calota vazia, para obter:
V(h) = 4Pi R³/3 - Pi (2R-h)²(R+h)/3
que pode ser simplificada para:
V(h) = Pi h²(3R-h)/3
Independentemente do fato que a altura h esteja no intervalo [0,R] ou [R,2R] ou de uma forma geral em
[0,2R], o cálculo do volume ocupado pelo líquido é dado por:
V(h) = Pi h²(3R-h)/3
Área Lateral de uma pirâmide
Às vezes podemos construir fórmulas para obter as áreas das superfícies que envolvem um determinado
sólido. Tal processo é conhecido como a planificação desse sólido. Isto pode ser realizado se tomarmos o
sólido de forma que a sua superfície externa seja feita de papelão ou algum outro material.
No caso da pirâmide, a idéia é tomar uma tesoura e cortar (o papelão d)a pirâmide exatamente sobre as
arestas, depois reunimos as regiões obtidas num plano que pode ser o plano de uma mesa.
As regiões planas obtidas são congruentes às faces laterais e também à base da pirâmide.

Se considerarmos uma pirâmide regular cuja base tem n lados e indicarmos por A(face) a área de uma face
lateral da pirâmide, então a soma das áreas das faces laterais recebe o nome de área lateral da pirâmide e
pode ser obtida por:
A(lateral) = n A(face)
Exemplo: Seja a pirâmide quadrangular regular que está planificada na figura acima, cuja aresta da base
mede 6cm e cujo apótema mede 4cm.
Como A(lateral)=n.A(face) e como a pirâmide é quadrangular temos n=4 triângulos isósceles, a área da face
lateral é igual à área de um dos triângulos, assim:
A(face) = b h/2 = 6.4/2 = 12A(face) = b h/2 = 6.4/2 = 12A(face) = b h/2 = 6.4/2 = 12A(face) = b h/2 = 6.4/2 = 12
A(lateral) = 4.12 = 48 cm²A(lateral) = 4.12 = 48 cm²A(lateral) = 4.12 = 48 cm²A(lateral) = 4.12 = 48 cm²
Exemplo: A aresta da base de uma pirâmide hexagonal regular mede 8 cm e a
altura 10 cm. Calcular a área lateral.
Tomaremos a aresta com a=8 cm e a altura com h=10 cm. Primeiro vamos
calcular a medida do apótema da face lateral da pirâmide hexagonal.
Calcularemos o raio r da base.
Como a base é um hexágono regular temos que r=(a/2)R[3], assim
r=8R[3]/2=4R[3] e pela relação de Pitágoras, segue que (ap)²=r²+h², logo:
(ap)²= (4R[3])²+10² = 48+100 = 148 = 4·37 = 2R[37]
A área da face e a área lateral, são dadas por:
A(face) = 8.2[37]/2 = 8.R[37]
A(lateral) = n.A(face) = 6.8.R[37] = 48.R[37]
Área total de uma Pirâmide
A área total de uma pirâmide é a soma da área da base com a área lateral, isto é:
A(total) = A(lateral) + A(base)
Exemplo: As faces laterais de uma pirâmide quadrangular regular formam ângulos de 60 graus com a base e
têm as arestas da base medindo 18 cm. Qual é a área total?
Já vimos que A(lateral)=n.A(face) e como cos(60º)=(lado/2)/a, então 1/2=9/a donde segue que a=18, assim:
A(face) = b.h/2 = (18.18)/2 = 162
A(lateral) = 4.162 = 648
A(base) = 18² = 324
Concluímos que:
A(total) = A(lateral) + A(base) = 648+324 = 970

Exemplo: Um grupo de escoteiros quer obter a área total de suas barracas, as
quais têm forma piramidal quadrangular. Para isso, eles usam medidas
escoteiras. Cada dois passos de um escoteiro mede 1 metro. A barraca tem 4
passos escoteiros de lado da base e 2 passos de apótema. Calcular a área da
base, área lateral e a área total.
A(base) = 2.2 = 4 m²
A(lateral) = 4.2.1 = 8 m³
Logo, a área total da barraca é
A(total) = A(lateral) + A(base) = 8+4 = 12 m²
Volume de uma Pirâmide
O volume de uma pirâmide pode ser obtido como um terço do produto da área da base pela altura da
pirâmide, isto é:
Volume = (1/3) A(base) h
Exemplo: Juliana tem um perfume contido em um frasco com a forma de uma
pirâmide regular com base quadrada. A curiosa Juliana quer saber o volume de
perfume que o frasco contém. Para isso ela usou uma régua e tirou duas
informações: a medida da aresta da base de 4cm e a medida da aresta lateral de
6cm.
Como V(pirâmide)=A(base).h/3, devemos calcular a área da base e a medida da
altura. Como a base tem forma quadrada de lado a=4cm, temos que
A(base)=a²=4cm.4cm=16 cm².
A altura h da pirâmide pode ser obtida como a medida de um
cateto de um triângulo retângulo cuja hipotenusa é dada pela
altura L=6cm da aresta lateral e o outro cateto Q=2×R[2] que é a
metade da medida da diagonal do quadrado. Dessa forma h²=L²-
Q², se onde segue que h²=36-8=28 e assim temos que h=2R[7] e
o volume será dado por V=(1/3).16.2R[7]=(32/3)R[7].
Seção Transversal de uma pirâmide
Seção transversal de uma pirâmide é a interseção da pirâmide com um plano paralelo à base da mesma. A
seção transversal tem a mesma forma que a base, isto é, as suas arestas correspondentes são proporcionais. A
razão entre uma aresta da seção transversal e uma aresta correspondente da base é dita razão de semelhança.
Observações sobre seções transversais:

1. Em uma pirâmide qualquer, a seção transversal e a base são regiões poligonais semelhantes. A razão
entre a área da seção transversal e a área da base é igual ao quadrado da razão de semelhança.
2. Ao seccionar uma pirâmide por um plano paralelo à base, obtemos outra pirâmide menor (acima do
plano) semelhante em todos os aspectos à pirâmide original.
3. Se duas pirâmides têm a mesma altura e as áreas das bases são iguais, então as seções transversais
localizadas à mesma distância do vértice têm áreas iguais.
V(seção)V(seção)V(seção)V(seção)
Volume da seção até o vérticeVolume da seção até o vérticeVolume da seção até o vérticeVolume da seção até o vértice
(volume da pirâmide menor)(volume da pirâmide menor)(volume da pirâmide menor)(volume da pirâmide menor)
V(piram)V(piram)V(piram)V(piram) Volume da pirâmide (maior)Volume da pirâmide (maior)Volume da pirâmide (maior)Volume da pirâmide (maior)
A(seção)A(seção)A(seção)A(seção)
Área da seção transversalÁrea da seção transversalÁrea da seção transversalÁrea da seção transversal
(base da pirâmide menor)(base da pirâmide menor)(base da pirâmide menor)(base da pirâmide menor)
A(base)A(base)A(base)A(base) Área da base da pirâmide (maior)Área da base da pirâmide (maior)Área da base da pirâmide (maior)Área da base da pirâmide (maior)
hhhh
Distância do vértice à seçãoDistância do vértice à seçãoDistância do vértice à seçãoDistância do vértice à seção
(altura da pirâmide menor)(altura da pirâmide menor)(altura da pirâmide menor)(altura da pirâmide menor)
HHHH Altura da pirâmide (maior)Altura da pirâmide (maior)Altura da pirâmide (maior)Altura da pirâmide (maior)
Assim:
V(base)V(base)V(base)V(base)
====
A(piram)A(piram)A(piram)A(piram)
····
hhhh
HHHH
A(base)A(base)A(base)A(base)
====
h²h²h²h²
H²H²H²H²
Então:
V(base)V(base)V(base)V(base)
====
h³h³h³h³
H³H³H³H³
Exemplo: Uma pirâmide tem a altura medindo 9cm e volume igual a 108cm³. Qual é o volume do tronco
desta pirâmide, obtido pelo corte desta pirâmide por um plano paralelo à base da mesma, sabendo-se que a

altura do tronco da pirâmide é 3cm?
Como
V(pirMenor)/V(pirâmide) = h³/H³
V(pirMenor)/108 = 6³/9³
V(pirMenor) = 32
então
V(tronco)=V(pirâmide)-V(pirMenor)= 108cm³-2cm³ = 76 cm³
Áreas e Volumes
Poliedro regularPoliedro regularPoliedro regularPoliedro regular ÁreaÁreaÁreaÁrea VolumeVolumeVolumeVolume
Tetraedro a2 R[3]a2 R[3]a2 R[3]a2 R[3] (1/12) a³ R[2](1/12) a³ R[2](1/12) a³ R[2](1/12) a³ R[2]
Hexaedro 6 a26 a26 a26 a2 a³a³a³a³
Octaedro 2 a2 R[3]2 a2 R[3]2 a2 R[3]2 a2 R[3] (1/3) a³ R[2](1/3) a³ R[2](1/3) a³ R[2](1/3) a³ R[2]
Dodecaedro 3a2 R{25+10·R[5]}3a2 R{25+10·R[5]}3a2 R{25+10·R[5]}3a2 R{25+10·R[5]} (1/4) a³ (15+7·R[5])(1/4) a³ (15+7·R[5])(1/4) a³ (15+7·R[5])(1/4) a³ (15+7·R[5])
Icosaedro 5a2 R[3]5a2 R[3]5a2 R[3]5a2 R[3] (5/12) a³ (3+R[5])(5/12) a³ (3+R[5])(5/12) a³ (3+R[5])(5/12) a³ (3+R[5])
Nesta tabela, a notação R[z] significa a raiz quadrada de z>0.Nesta tabela, a notação R[z] significa a raiz quadrada de z>0.Nesta tabela, a notação R[z] significa a raiz quadrada de z>0.Nesta tabela, a notação R[z] significa a raiz quadrada de z>0.
Volume de um prisma
O volume de um prisma é dado por:
V(prisma) = A(base).h
Área lateral do prisma reto com base poligonal regular
A área lateral de um prisma reto que tem por base uma região poligonal regular de n lados é dada pela soma
das áreas das faces laterais. Como neste caso todas as áreas das faces laterais são iguais, basta tomar a área
lateral como:
A(lateral) = n A(Face Lateral)
Uma forma alternativa para obter a área lateral de um prisma reto tendo como base um polígono regular de
n lados é tomar P como o perímetro desse polígono e h como a altura do prisma.
A(lateral) = P.h
Tronco de prisma

Quando seccionamos um prisma por um plano não paralelo aos planos das
bases, a região espacial localizada dentro do prisma, acima da base inferior e
abaixo do plano seccionante é denominado tronco de prisma. Para calcular o
volume do tronco de prisma, multiplicamos a média aritmética das arestas
laterais do tronco de prisma pela área da base.
Números Complexos
Na resolução de uma equação algébrica, um fator fundamental é o conjunto universo que representa o
contexto onde poderemos encontrar as soluções. Por exemplo, se estivermos trabalhando no conjunto dos
números racionais, a equação 2x+7=0, terá uma única solução dada por x=-7/2. assim, o conjunto solução
será:
S = { 7/2 }
mas, se estivermos procurando por um número inteiro como resposta, o conjunto solução será o conjunto
vazio, isto é:
S = Ø = { }
De forma análoga, ao tentar obter o conjunto solução para a equação x2+1=0 sobre o conjunto dos números
reais, obteremos como resposta o conjunto vazio, isto é:
S = Ø = { }
o que significa que não existe um número real que elevado ao quadrado seja igual a -1, mas se seguirmos o
desenvolvimento da equação pelos métodos comuns, obteremos:
x = R[-1] =
onde R[-1] é a raiz quadrada do número real -1. Isto parece não ter significado prático e foi por esta razão
que este número foi chamado imaginário, mas o simples fato de substituir R[-1] pela letra i (unidade
imaginária) e realizar operações como se estes números fossem polinômios, faz com que uma série de
situações tanto na Matemática como na vida, tenham sentido prático de grande utilidade e isto nos leva à
teoria dos números complexos.
Definição de número complexo
Número complexo é todo número que pode ser escrito na forma
z = a + b i

onde a e b são números reais e i é a unidade imaginária. O número real a é a parte real do número complexo
z e o número real b é a parte imaginária do número complexo z, denotadas por:
a = Re(z) e b = Im(z)
Exemplos de tais números são apresentados na tabela.
Número complexoNúmero complexoNúmero complexoNúmero complexo Parte realParte realParte realParte real Parte imagináriaParte imagináriaParte imagináriaParte imaginária
2 + 3 i2 + 3 i2 + 3 i2 + 3 i 2222 3333
2 - 3 i2 - 3 i2 - 3 i2 - 3 i 2222 -3-3-3-3
2222 2222 0000
3 i3 i3 i3 i 0000 3333
-3 i-3 i-3 i-3 i 0000 -3-3-3-3
0000 0000 0000
Observação: O conjunto de todos os números complexos é denotado pela letra C e o conjunto dos números
reais pela letra R. Como todo número real x pode ser escrito como um número complexo da forma z=x+yi,
onde y=0 então assumiremos que o conjunto dos números reais está contido no conjunto dos números
complexos.
Elementos complexos especiais
1. Igualdade de números complexos: Dados os números complexos z=a+bi e w=c+di, definimos a
igualdade entre z e w, escrevendo
z = w se, e somente se, a = c e b = d
Para que os números complexos z=2+yi e w=c+3i sejam iguais, deveremos ter que c=2 e y=3.
2. Oposto de um número complexo: O oposto do número complexo z=a+bi é o número complexo
denotado por -z=-(a+bi), isto é:
-z = Oposto(a+bi) = (-a) + (-b)i
O oposto de z=-2+3i é o número complexo -z=2-3i.
3. Conjugado de um número complexo: O número complexo conjugado de z=a+bi é o número
complexo denotado por z*=a-bi, isto é:
z* = conjugado(a+bi) = a + (-b)i
O conjugado de z=2-3i é o número complexo z*=2+3i.
Operações básicas com números complexos
Dados os números complexos z=a+bi e w=c+di, podemos definir duas operações fundamentais, adição e
produto, agindo sobre eles da seguinte forma:
z+w = (a+bi) + (c+di) = (a+c) + (b+d)i
z.w = (a+bi).(c+di) = (ac-bd) + (ad+bc)i
Observação: Tais operações lembram as operações com expressões polinomiais, pois a adição é realizada de

uma forma semelhante, isto é: (a+bx)+(c+dx)=(a+c)+(b+d)x e a multiplicação (a+bx).(c+dx), é realizada
através de um algoritmo que aparece na forma:
a + b x
c + d x X
_________________
ac + bcx
adx + bdx²
______________________
ac + (bc+ad)x + bdx²
de forma que devemos substituir x2 por -1.
Exemplos:
1. Se z=2+3i e w=4-6i, então z+w=(2+3i)+(4-6i)=6-3i.
2. Se z=2+3i e w=4-6i, então z.w=(2+3i).(4-6i)=-4+0i.
Potências e curiosidade sobre a unidade imaginária
Potências de i: Ao tomar i=R[-1], temos uma sequência de valores muito simples para as potências de i:
PotênciaPotênciaPotênciaPotência i2i2i2i2 i3i3i3i3 i4i4i4i4 i5i5i5i5 i6i6i6i6 i7i7i7i7 i8i8i8i8 i9i9i9i9
ValorValorValorValor -1-1-1-1 -i-i-i-i 1111 iiii -1-1-1-1 -i-i-i-i 1111 iiii
Pela tabela acima podemos observar que as potência de i cujos expoentes são múltiplos de 4, fornecem o
resultado 1, logo toda potência de i pode ter o expoente decomposto em um múltiplo de 4 mais um resto
que poderá ser 0, 1, 2 ou 3. Dessa forma podemos calcular rapidamente qualquer potência de i, apenas
conhecendo o resto da divisão do expoente por 4.
Exercício: Calcular os valores dos números complexos: i402, i4033 e i1998. Como exemplo: i402=i400.i2 = 1.
(-1) = -1
Curiosidade geométrica sobre i: Ao pensar um número complexo z=a+bi como um vetor z=(a,b) no plano
cartesiano, a multiplicação de um número complexo z=a+bi pela unidade imaginária i, resulta em um outro
número complexo w=-b+ai, que forma um ângulo reto (90 graus) com o número complexo z=a+bi dado.
Exercício: Tomar um número complexo z, multiplicar por i para obter z1=i.z, depois multiplicar o resultado
z1 por i para obter z2=i.z1. Continue multiplicando os resultados obtidos por i até ficar cansado ou então
use a inteligência para descobrir algum fato geométrico significativo neste contexto. Após constatar que
você é inteligente, faça um desenho no plano cartesiano contendo os resultados das multiplicações.
O inverso de um número complexo
Dado o número complexo z=a+bi, não nulo (a ou b deve ser diferente de zero) definimos o inverso de z
como o número z-1=u+iv, tal que
z . z-1 = 1

O produto de z pelo seu inverso z-1 deve ser igual a 1, isto é:
(a+bi).(u+iv) = (au-bv)+(av+bu)i = 1 = 1+0.i
o que nos leva a um sistema com duas equações e duas incógnitas:
a u - b v = 1
b u + a v = 0
Este sistema pode ser resolvido pela regra de Cramér e possui uma única solução (pois a ou b são diferentes
de zero), fornecendo:
u = a/(a2+b2)
v = -b/(a2+b2)
assim, o inverso do número complexo z=a+bi é:
Obtenção do inverso de um número complexo: Para obter o inverso de um número complexo, por exemplo,
o inverso de z=5+12i, deve-se:
1. Escrever o inverso desejado na forma de uma fração
2. Multiplicar o numerador e o denominador da fração pelo conjugado de z
3. Lembrar que i2 = -1, simplificar os números complexos pela redução dos termos semelhantes, para
obter
Diferença e divisão de números complexos
Diferença de números complexos: A diferença entre os números complexos z=a+bi e w=c+di é o número
complexo obtido pela soma entre z e -w, isto é: z-w=z+(-w).
Exemplo: A diferença entre os complexos z=2+3i e w=5+12i é z-w=(2+3i)+(-5-12i)=(2-5)+(3-12)i=-3-9i.
Divisão de números complexos: A divisão entre os números complexos z=a+bi e w=c+di (w não nulo) é
definida como o número complexo obtido pelo produto entre z e w-1, isto é: z/w=z.w-1.
Exemplo: Para dividir o número complexo z=2+3i por w=5+12i, basta multiplicar o numerador e o
denominador da fração z/w pelo conjugado de w:
Representação geométrica de um número complexo

Um número complexo da forma z=a+bi, pode ser representado do ponto de vista geométrico no plano
cartesiano, como um ponto (par ordenado) tomando-se a abscissa deste ponto como a parte real do número
complexo a no eixo OX e a ordenada como a parte imaginária do número complexo z no eixo OY, sendo
que o número complexo 0=0+0i é representado pela própria origem (0,0) do sistema.
Módulo e argumento de um número complexo
Módulo de um número complexo: No gráfico anterior observamos que existe um triângulo retângulo cuja
medida da hipotenusa é a distância da origem 0 ao número complexo z, normalmente denotada pela letra
grega ro nos livros, mas aqui denotada por r, o cateto horizontal tem comprimento igual à parte real a do
número complexo e o cateto vertical corresponde à parte imaginária b do número complexo z.
Desse modo, se z=a+bi é um número complexo, então r2=a2+b2 e a medida da hipotenusa será por
definição, o módulo do número complexo z, denotado por |z|, isto é:
Argumento de um número complexo: O ângulo ø formado entre o segmento OZ e o eixo OX, é
denominado o argumento do número complexo z. Pelas definições da trigonometria circular temos as três
relações:
cos(ø)=a/r, sen(ø)/r, tan(ø)=b/a
Por experiência, observamos que é melhor usar o cosseno ou o seno do ângulo para definir bem o
argumento, uma vez que a tangente apresenta alguns problemas.
Forma polar e sua multiplicação
Forma polar de um número complexo: Das duas primeiras relações trigonométricas apresentadas
anteriormente, podemos escrever:
z = a+bi = r cos(ø) + r i sen(ø) = r (cos ø + i sen ø)
e esta última é a forma polar do número complexo z.
Multiplicação de complexos na forma polar: Consideremos os números complexos:
z = r (cos m + i sen m)
w = s (cos n + i sen n)
onde, respectivamente, r e s são os módulos e m e n são os argumentos destes números complexos z e w.
Realizamos o produto entre estes números da forma usual e reescrevemos o produto na forma:
z . w = r s [cos (m+n) + i sen (m+n)]
Este fato é garantido pelas relações:
cos(m+n) = cos(m) cos(n) - sen(m) sen(n)
sen(m+n) = sen(m) cos(n) + sen(n) cos(m)

Potência de um número complexo na forma polar
Seguindo o produto acima, poderemos obter a potência de ordem k de um número complexo. Como
z = r [cos(m) + i sen(m)]
então
zk = rk [cos(km) + i sen(km)]
Exemplo: Consideremos o número complexo z=1+i, cujo módulo é a raiz quadrada de 2 e o argumento é
/4 (45 graus). Para elevar este número à potência 16, basta escrever:
z16 = 28[cos(720o)+isen(720o)]=256
Raiz quarta de um número complexo
Um ponto fundamental que valoriza a existência dos números complexos é a possibilidade de extrair a raiz
de ordem 4 de um número complexo, mesmo que ele seja um número real negativo, o que significa,
resolver uma equação algébrica do 4o. grau. Por exemplo, para extrair a raiz quarta do número -16,
devemos obter as quatro raízes da equação algébrica x4+16=0.
Antes de apresentar o nosso processo para a obtenção da raiz quarta de um número complexo w,
necessitamos saber o seu módulo r e o seu argumento t, o que significa poder escrever o número complexo
na forma polar:
w = r (cos t + i sen t)
O primeiro passo é realizar um desenho mostrando este número complexo w em um círculo de raio r e
observar o argumento t, dado pelo angulo entre o eixo OX e o número complexo w.
O passo seguinte é obter um outro número complexo z(1) cujo módulo seja a raiz quarta de r e cujo
argumento seja t/4. Este número complexo é a primeira das quatro raizes complexas procuradas.
z(1) = r1/4 [cos(t/4)+isen(t/4)]
As outras raízes serão:
z(2) = i z(1)
z(3) = i z(2)
z(4) = i z(3)
Todas aparecem no gráfico, mas observamos que este processo para obter as quatro raízes do número
complexo w ficou mais fácil pois temos a propriedade geométrica que o número complexo i multiplicado
por outro número complexo, roda este último de 90 graus e outro fato interessante é que todas as quatro
raízes de w estão localizadas sobre a mesma circunferência e os ângulos formados entre duas raízes
consecutivas é de 90 graus.

Se os quatro números complexos forem ligados, aparecerá um quadrado rodado de t/4 radianos em relação
ao eixo OX.
Raiz n-ésima de um número complexo
Existe uma importantíssima relação atribuída a Euler:
ei.t = cos(t) + i sen(t)
que é verdadeira para todo argumento real e a constante e tem o valor aproximado 2,71828... Para facilitar a
escrita usamos frequentemente:
exp(i t) = cos(t) + i sen(t)
Observação: A partir da relação de Euler, é possível construir uma relação notável envolvendo os mais
importantes sinais e constantes da Matemática:
Voltemos agora à exp(it). Se multiplicarmos o número eit por um número complexo z, o resultado será um
outro número complexo rodado de t radianos em relação ao número complexo z.
Por exemplo, se multiplicarmos o número complexo z por exp(i /8)=cos( /8)+i sen(
/8), obteremos um número complexo z(1) que forma com z um ângulo /8=22,5graus,
no sentido anti-horário.
Iremos agora resolver a equação xn=w, onde n é um número natural e w é um número complexo dado. Da
mesma forma que antes, podemos escrever o número complexo w=r(cos t + i sen t) e usar a relação de Euler,
para obter:
w = r eit
Para extrair a raiz n-ésima, deve-se construir a primeira raiz que é dada pelo número complexo
z(1) = r1/n eit/n
Todas as outras n-1 raízes serão obtidas pela multiplicação recursiva dada por:
z(k) = z(k-1) e2i /n
onde k varia de 2 até n.
Exemplo: Para obter a primeira raiz da equação x8=-64, observamos a posição do número complexo w=-
64+0i, constatando que o seu módulo é igual a 64 e o argumento é igual a radianos (=180 graus).

Aqui, a raiz oitava de 64 é igual a 2 e o argumento da primeira raiz é /8, então z(1) pode ser
escrita na forma polar:
z(1) = 2 ei /8 = 2(cos 22,5o+i sen 22,5o) = R[2](1+i)
onde R[2] é a raiz quadrada de 2. Obtemos as outras raízes pela multiplicação do número complexo abaixo,
através de qualquer uma das formas:
e2i /8 = 2(cos 45o + i sen 45o) = R[2](1+i)/2=0,707(1+i)
Assim:
z(2) = z(1) R[2](1+i)/2
z(3) = z(2) R[2](1+i)/2
z(4) = z(3) R[2](1+i)/2
z(5) = z(4) R[2](1+i)/2
z(6) = z(5) R[2](1+i)/2
z(7) = z(6) R[2](1+i)/2
z(8) = z(7) R[2](1+i)/2
Exercício: Construa no sistema cartesiano os 8 números complexos e ligue todas as raízes consecutivas para
obter um octógono regular rodado de 22,5 graus em relação ao eixo OX. Tente comparar este método com
outros que você conhece e realize exercícios para observar como aconteceu o aprendizado.
Número complexo como matriz
Existe um estudo sobre números complexos, no qual um número complexo z=a+bi pode ser tratado como
uma matriz quadrada 2x2 da forma:
e todas as propriedades dos números complexos, podem ser obtidas através de matrizes, resultando em
processos que transformam as características geométricas dos números complexos em algo simples.
ESTATÍSTICA
 É uma parte da matemática aplicada que fornece métodos para coleta, organização, descrição, análise
e interpretação de dados e para a utilização dos mesmos na tomada de decisões.
 A coleta, a organização ,a descrição dos dados, o cálculo e a interpretação de coeficientes pertencem
à ESTATÍSTICA DESCRITIVA, enquanto a análise e a interpretação dos dados, associado a uma margem de
incerteza, ficam a cargo da ESTATÍSTICA INDUTIVA ou INFERENCIAL, também chamada como a

medida da incerteza ou métodos que se fundamentam na teoria da probabilidade.
.
2. ORGANIZAÇÃO DE DADOS ESTATÍSTICOS
FASES DO MÉTODO ESTATÍSTICO
1º - DEFINIÇÃO DO PROBLEMA : Saber exatamente aquilo que se pretende pesquisar é o mesmo
que definir corretamente o problema.
2º - PLANEJAMENTO : Como levantar informações ? Que dados deverão ser obtidos ? Qual
levantamento a ser utilizado? Censitário? Por amostragem? E o cronograma de atividades ? Os custos
envolvidos ? etc.
3º - COLETA DE DADOS: Fase operacional. É o registro sistemático de dados, com um objetivo
determinado.
Dados primários: quando são publicados pela própria pessoa ou organização que os haja recolhido. Ex:
tabelas do censo demográfico do IBGE.
Dados secundários: quando são publicados por outra organização. Ex: quando determinado jornal publica
estatísticas referentes ao censo demográfico extraídas do IBGE.
OBS: É mais seguro trabalhar com fontes primárias. O uso da fonte secundária traz o grande risco de erros
de transcrição.
Coleta Direta: quando é obtida diretamente da fonte. Ex: Empresa que realiza uma pesquisa para
saber a preferência dos consumidores pela sua marca.
coleta contínua: registros de nascimento, óbitos, casamentos;
coleta periódica: recenseamento demográfico, censo industrial;
coleta ocasional: registro de casos de dengue.

Coleta Indireta: É feita por deduções a partir dos elementos conseguidos pela coleta direta, por
analogia, por avaliação,indícios ou proporcionalização.
4º - APURAÇÃO DOS DADOS: Resumo dos dados através de sua contagem e agrupamento. É a
condensação e tabulação de dados.
5º - APRESENTAÇÃO DOS DADOS: Há duas formas de apresentação, que não se excluem
mutuamente. A apresentação tabular, ou seja é uma apresentação numérica dos dados em linhas e colunas
distribuídas de modo ordenado, segundo regras práticas fixadas pelo Conselho Nacional de Estatística. A
apresentação gráfica dos dados numéricos constitui uma apresentação geométrica permitindo uma visão
rápida e clara do fenômeno.
6º - ANÁLISE E INTERPRETAÇÃO DOS DADOS: A última fase do trabalho estatístico é a mais
importante e delicada. Está ligada essencialmente ao cálculo de medidas e coeficientes, cuja finalidade
principal é descrever o fenômeno (estatística descritiva).
DEFINIÇÕES BÁSICAS DA ESTATÍSTICA
.
FENÔMENO ESTATÍSTICO: é qualquer evento que se pretenda analisar, cujo estudo seja possível a
aplicação do método estatístico. São divididos em três grupos:
Fenômenos de massa ou coletivo: são aqueles que não podem ser definidos por uma simples observação. A
estatística dedica-se ao estudo desses fenômenos. Ex: A natalidade na Grande Vitória, O preço médio da
cerveja no Espírito Santo, etc.
Fenômenos individuais: são aqueles que irão compor os fenômenos de massa. Ex: cada nascimento na
Grande Vitória, cada preço de cerveja no Espírito Santo, etc.
Fenômenos de multidão: quando as características observadas para a massa não se verificam para o
particular.
DADO ESTATÍSTICO: é um dado numérico e é considerado a matéria-prima sobre a qual iremos
aplicar os métodos estatísticos.

POPULAÇÃO: é o conjunto total de elementos portadores de, pelo menos, uma característica comum.
AMOSTRA: é uma parcela representativa da população que é examinada com o propósito de tirarmos
conclusões sobre a essa população.
PARÂMETROS: São valores singulares que existem na população e que servem para caracterizá-la. Para
definirmos um parâmetro devemos examinar toda a população. Ex: Os alunos do 2º ano da FACEV têm em
média 1,70 metros de estatura.
ESTIMATIVA: é um valor aproximado do parâmetro e é calculado com o uso da amostra.
ATRIBUTO: quando os dados estatísticos apresentam um caráter qualitativo, o levantamento e os estudos
necessários ao tratamento desses dados são designados genericamente de estatística de atributo.
VARIÁVEL: É o conjunto de resultados possíveis de um fenômeno.
VARIÁVEL QUALITATIVA: Quando seu valores são expressos por atributos: sexo, cor da pele,etc.
VARIÁVEL QUANTITATIVA: Quando os dados são de caráter nitidamente quantitativo, e o conjunto
dos resultados possui uma estrutura numérica, trata-se portanto da estatística de variável e se dividem em :
VARIÁVEL DISCRETA OU DESCONTÍNUA: Seus valores são expressos geralmente através de números
inteiros não negativos. Resulta normalmente de contagens. Ex: Nº de alunos presentes às aulas de
introdução à estatística econômica no 1º semestre de 1997: mar = 18 , abr = 30 , mai = 35 , jun = 36.
VARIÁVEL CONTÍNUA: Resulta normalmente de uma mensuração, e a escala numérica de seus
possíveis valores corresponde ao conjunto R dos números Reais, ou seja, podem assumir, teoricamente,
qualquer valor entre dois limites. Ex.: Quando você vai medir a temperatura de seu corpo com um
termômetro de mercúrio o que ocorre é o seguinte: O filete de mercúrio, ao dilatar-se, passará por todas as

temperaturas intermediárias até chegar na temperatura atual do seu corpo.
Exemplos -
. Cor dos olhos das alunas: qualitativa
. Índice de liquidez nas indústrias capixabas: quantitativa contínua
. Produção de café no Brasil: quantitativa contínua
. Número de defeitos em aparelhos de TV: quantitativa discreta
. Comprimento dos pregos produzidos por uma empresa: quantitativa contínua
. O ponto obtido em cada jogada de um dado: quantitativa discreta
AMOSTRAGEM
MÉTODOS PROBABILÍSTICOS
 Exige que cada elemento da população possua determinada probabilidade de ser selecionado.
Normalmente possuem a mesma probabilidade. Assim, se N for o tamanho da população, a probabilidade
de cada elemento ser selecionado será 1/N. Trata-se do método que garante cientificamente a aplicação das
técnicas estatísticas de inferências. Somente com base em amostragens probabilísticas é que se podem
realizar inferências ou induções sobre a população a partir do conhecimento da amostra.
É uma técnica especial para recolher amostras, que garantem, tanto quanto possível, o
acaso na escolha.
.
AMOSTRAGEM CASUAL ou ALEATÓRIA SIMPLES
 É o processo mais elementar e freqüentemente utilizado. É equivalente a um sorteio lotérico. Pode
ser realizada numerando-se a população de 1 a n e sorteando-se, a seguir, por meio de um dispositivo
aleatório qualquer, x números dessa seqüência, os quais corresponderão aos elementos pertencentes à
amostra.

Ex: Vamos obter uma amostra, de 10%, representativa para a pesquisa da estatura de 90 alunos de uma
escola:
1º - numeramos os alunos de 1 a 90.
2º - escrevemos os números dos alunos, de 1 a 90, em pedaços iguais de papel, colocamos na urna e após
mistura retiramos, um a um, nove números que formarão a amostra.
OBS: quando o número de elementos da amostra é muito grande, esse tipo de sorteio torna-se muito
trabalhoso. Neste caso utiliza-se uma Tabela de números aleatórios, construída de modo que os algarismos
de 0 a 9 são distribuídos ao acaso nas linhas e colunas.
.
.AMOSTRAGEM PROPORCIONAL ESTRATIFICADA:
 Quando a população se divide em estratos (sub-populações), convém que o sorteio dos elementos da
amostra leve em consideração tais estratos, daí obtemos os elementos da amostra proporcional ao número
de elementos desses estratos.
Ex: Vamos obter uma amostra proporcional estratificada, de 10%, do exemplo anterior, supondo, que, dos
90 alunos, 54 sejam meninos e 36 sejam meninas. São portanto dois estratos (sexo masculino e sexo
feminino). Logo, temos:
SEXO
POPULACÃ
O
10 % AMOSTRA
MASC. 54 5,4 5
FEMIN. 36 3,6 4
Total 90 9,0 9
Numeramos então os alunos de 01 a 90, sendo 01 a 54 meninos e 55 a 90, meninas e procedemos o sorteio
casual com urna ou tabela de números aleatórios.
.
AMOSTRAGEM SISTEMÁTICA:
 Quando os elementos da população já se acham ordenados, não há necessidade de construir o
sistema de referência. São exemplos os prontuários médicos de um hospital, os prédios de uma rua, etc.
Nestes casos, a seleção dos elementos que constituirão a amostra pode ser feita por um sistema imposto pelo
pesquisador.

Ex: Suponhamos uma rua com 900 casas, das quais desejamos obter uma amostra formada por 50 casas para
uma pesquisa de opinião. Podemos, neste caso, usar o seguinte procedimento: como 900/50 = 18,
escolhemos por sorteio casual um número de 01 a 18, o qual indicaria o primeiro elemento sorteado para a
amostra; os demais elementos seriam periodicamente considerados de 18 em 18. Assim, suponhamos que o
número sorteado fosse 4 a amostra seria: 4ª casa, 22ª casa, 40ª casa, 58ª casa, 76ª casa, etc.
AMOSTRAGEM POR CONGLOMERADOS (ou AGRUPAMENTOS)
 Algumas populações não permitem, ou tornam extremamente difícil que se identifiquem seus
elementos. Não obstante isso, pode ser relativamente fácil identificar alguns subgrupos da população. Em
tais casos, uma amostra aleatória simples desses subgrupos (conglomerados) pode se colhida, e uma
contagem completa deve ser feita para o conglomerado sorteado. Agrupamentos típicos são quarteirões,
famílias, organizações, agências, edifícios etc.
Ex: Num levantamento da população de determinada cidade, podemos dispor do mapa indicando cada
quarteirão e não dispor de uma relação atualizada dos seus moradores. Pode-se, então, colher uma amostra
dos quarteirões e fazer a contagem completa de todos os que residem naqueles quarteirões sorteados.
MÉTODOS NÃO PROBABILÍSITCOS
 São amostragens em que há uma escolha deliberada dos elementos da amostra. Não é possível
generalizar os resultados das pesquisas para a população, pois as amostras não-probabilísticas não garantem
a representatividade da população.
AMOSTRAGEM ACIDENTAL
 Trata-se de uma amostra formada por aqueles elementos que vão aparecendo, que são possíveis de se
obter até completar o número de elementos da amostra. Geralmente utilizada em pesquisas de opinião, em
que os entrevistados são acidentalmente escolhidos.
Ex: Pesquisas de opinião em praças públicas, ruas de grandes cidades;

AMOSTRAGEM INTENCIONAL
 De acordo com determinado critério, é escolhido intencionalmente um grupo de elementos que irão
compor a amostra. O investigador se dirige intencionalmente a grupos de elementos dos quais deseja saber a
opinião.
Ex: Numa pesquisa sobre preferência por determinado cosmético, o pesquisador se dirige a um grande salão
de beleza e entrevista as pessoas que ali se encontram.
AMOSTRAGEM POR QUOTAS
 Um dos métodos de amostragem mais comumente usados em levantamentos de mercado e em
prévias eleitorais. Ele abrange três fases:
1ª - classificação da população em termos de propriedades que se sabe, ou presume, serem relevantes para a
característica a ser estudada;
2ª - determinação da proporção da população para cada característica, com base na constituição conhecida,
presumida ou estimada, da população;
3ª - fixação de quotas para cada entrevistador a quem tocará a responsabilidade de selecionar entrevistados,
de modo que a amostra total observada ou entrevistada contenha a proporção e cada classe tal como
determinada na 2ª fase.
Ex: Numa pesquisa sobre o "trabalho das mulheres na atualidade", provavelmente se terá interesse em
considerar: a divisão cidade e campo, a habitação, o número de filhos, a idade dos filhos, a renda média, as
faixas etárias etc.
A primeira tarefa é descobrir as proporções (porcentagens) dessas características na população. Imagina-se
que haja 47% de homens e 53% de mulheres na população. Logo, uma amostra de 50 pessoas deverá ter 23
homens e 27 mulheres. Então o pesquisador receberá uma "quota" para entrevistar 27 mulheres. A
consideração de várias categorias exigirá uma composição amostral que atenda ao n determinado e às
proporções populacionais estipuladas.
.

SÉRIES ESTATÍSTICAS
TABELA: É um quadro que resume um conjunto de dados dispostos segundo linhas e colunas de
maneira sistemática.
• De acordo com a Resolução 886 do IBGE, nas casas ou células da tabela devemos colocar :
um traço horizontal ( - ) quando o valor é zero;
três pontos ( ... ) quando não temos os dados;
zero ( 0 ) quando o valor é muito pequeno para ser expresso pela unidade utilizada;
um ponto de interrogação ( ? ) quando temos dúvida quanto à exatidão de
determinado valor.
Obs: O lado direito e esquerdo de uma tabela oficial deve ser aberto..
SÉRIE ESTATÍSTICA: É qualquer tabela que apresenta a distribuição de um conjunto de dados
estatísticos em função da época, do local ou da espécie.
Séries Homógradas: são aquelas em que a variável descrita apresenta variação discreta ou descontínua.
Podem ser do tipo temporal, geográfica ou específica.
a) Série Temporal: Identifica-se pelo caráter variável do fator cronológico. O local e a espécie
(fenômeno) são elementos fixos. Esta série também é chamada de histórica ou evolutiva.
ABC VEÍCULOS LTDA.
Vendas no 1º bimestre de 1996
PERÍODO UNIDADES VENDIDAS
JAN/96 20000

FEV/96 10000
TOTAL 30000
.
b) Série Geográfica: Apresenta como elemento variável o fator geográfico. A época e o fato (espécie) são
elementos fixos. Também é chamada de espacial, territorial ou de localização.
ABC VEÍCULOS LTDA.
FILIAIS UNIDADES VENDIDAS
São Paulo 13000
Rio de Janeiro 17000
TOTAL 30000
c) Série Específica: O caráter variável é apenas o fato ou espécie. Também é chamada de série categórica.
ABC VEÍCULOS LTDA.
MARCA UNIDADES VENDIDAS *
FIAT 18000
GM 12000
TOTAL 30000
SÉRIES CONJUGADAS: Também chamadas de tabelas de dupla entrada. São apropriadas à
apresentação de duas ou mais séries de maneira conjugada, havendo duas ordens de classificação: uma
horizontal e outra vertical. O exemplo abaixo é de uma série geográfica-temporal.
ABC VEÍCULOS LTDA.

FILIAIS Janeiro/96 Fevereiro/96
São Paulo 10000 3000
Rio de Janeiro 12000 5000
TOTAL 22000 8000
GRÁFICOS ESTATÍSTICOSG
 São representações visuais dos dados estatísticos que devem corresponder, mas nunca substituir as
tabelas estatísticas.
Características: Uso de escalas, sistema de coordenadas, simplicidade, clareza e veracidade.
Gráficos de informação: São gráficos destinados principalmente ao público em geral, objetivando
proporcionar uma visualização rápida e clara. São gráficos tipicamente expositivos, dispensando
comentários explicativos adicionais. As legendas podem ser omitidas, desde que as informações desejadas
estejam presentes.
Gráficos de análise: São gráficos que prestam-se melhor ao trabalho estatístico, fornecendo elementos úteis
à fase de análise dos dados, sem deixar de ser também informativos. Os gráficos de análise freqüentemente
vêm acompanhados de uma tabela estatística. Inclui-se, muitas vezes um texto explicativo, chamando a
atenção do leitor para os pontos principais revelados pelo gráfico.
• Uso indevido de Gráficos: Podem trazer uma idéia falsa dos dados que estão sendo analisados,
chegando mesmo a confundir o leitor. Trata-se, na realidade, de um problema de construção de
escalas.
.
Classificação dos gráficos: Diagramas, Estereogramas, Pictogramas e Cartogramas.
.
1 - Diagramas:

 São gráficos geométricos dispostos em duas dimensões. São os mais usados na representação de séries
estatísticas. Eles podem ser :
1.1- Gráficos em barras horizontais.
1.2- Gráficos em barras verticais ( colunas ).
• Quando as legendas não são breves usa-se de preferência os gráficos em barras horizontais. Nesses
gráficos os retângulos têm a mesma base e as alturas são proporcionais aos respectivos dados.
A ordem a ser observada é a cronológica, se a série for histórica, e a
decrescente, se for geográfica ou categórica.
1.2- Gráficos em barras compostas.
1.4- Gráficos em colunas superpostas.
• Eles diferem dos gráficos em barras ou colunas convencionais apenas pelo fato de apresentar cada
barra ou coluna segmentada em partes componentes. Servem para representar comparativamente
dois ou mais atributos.
1.5- Gráficos em linhas ou lineares.
• São freqüentemente usados para representação de séries cronológicas com um grande número de
períodos de tempo. As linhas são mais eficientes do que as colunas, quando existem intensas
flutuações nas séries ou quando há necessidade de se representarem várias séries em um mesmo
gráfico.
• Quando representamos, em um mesmo sistema de coordenadas, a variação de dois fenômenos, a
parte interna da figura formada pelos gráficos desses fenômenos é denominada de área de excesso.
1.5- Gráficos em setores.
• Este gráfico é construído com base em um círculo, e é empregado sempre que desejamos ressaltar a
participação do dado no total. O total é representado pelo círculo, que fica dividido em tantos
setores quantas são as partes. Os setores são tais que suas áreas são respectivamente proporcionais aos
dados da série. O gráfico em setores só deve ser empregado quando há, no máximo, sete dados.

• Obs: As séries temporais geralmente não são representadas por este tipo de gráfico.
.
2 - Estereogramas:
 São gráficos geométricos dispostos em três dimensões, pois representam volume. São usados nas
representações gráficas das tabelas de dupla entrada. Em alguns casos este tipo de gráfico fica difícil de ser
interpretado dada a pequena precisão que oferecem.
.
3 - Pictogramas:
 São construídos a partir de figuras representativas da intensidade do fenômeno. Este tipo de gráfico
tem a vantagem de despertar a atenção do público leigo, pois sua forma é atraente e sugestiva. Os símbolos
devem ser auto-explicativos. A desvantagem dos pictogramas é que apenas mostram uma visão geral do
fenômeno, e não de detalhes minuciosos. Veja o exemplo abaixo:
4- Cartogramas:
 São ilustrações relativas a cartas geográficas (mapas). O objetivo desse gráfico é o de figurar os dados
estatísticos diretamente relacionados com áreas geográficas ou políticas.
DISTRIBUIÇÃO DE FREQÜÊNCIA
 É um tipo de tabela que condensa uma coleção de dados conforme as freqüências (repetições de seus
valores).

Tabela primitiva ou dados brutos: É uma tabela ou relação de elementos que não foram numericamente
organizados. É difícil formarmos uma idéia exata do comportamento do grupo como um todo, a partir de
dados não ordenados.
Ex : 45, 41, 42, 41, 42 43, 44, 41 ,50, 46, 50, 46, 60, 54, 52, 58, 57, 58, 60, 51
ROL: É a tabela obtida após a ordenação dos dados (crescente ou decrescente).
Ex : 41, 41, 41, 42, 42 43, 44, 45 ,46, 46, 50, 50, 51, 52, 54, 57, 58, 58, 60, 60
Distribuição de freqüência sem intervalos de classe: É a simples condensação dos dados conforme as
repetições de seu valores. Para um ROL de tamanho razoável esta distribuição de freqüência é
inconveniente, já que exige muito espaço. Veja exemplo abaixo:
Dados Freqüência
41 3
42 2
43 1
44 1
45 1
46 2
50 2
51 1
52 1
54 1
57 1
58 2
60 2
Total 20
Distribuição de freqüência com intervalos de classe:Quando o tamanho da amostra é elevado, é mais
racional efetuar o agrupamento dos valores em vários intervalos de classe.
Classes Freqüências
41 |------- 45 7
45 |------- 49 3

49 |------- 53 4
53 |------- 57 1
57 |------- 61 5
Total 20
ELEMENTOS DE UMA DISTRIBUIÇÃO DE FREQÜÊNCIA (com intervalos de classe) 
CLASSE: são os intervalos de variação da variável e é simbolizada por i e o número total de classes
simbolizada por k. Ex: na tabela anterior k = 5 e 49 |------- 53 é a 3ª classe, onde i = 3.
LIMITES DE CLASSE: são os extremos de cada classe. O menor número é o limite inferior de classe ( li
) e o maior número, limite superior de classe ( Li ). Ex: em 49 |------- 53,... l3 = 49 e L3 = 53. O símbolo
|------- representa um intervalo fechado à esquerda e aberto à direita. O dado 53 do ROL não pertence a
classe 3 e sim a classe 4 representada por 53 |------- 57.
AMPLITUDE DO INTERVALO DE CLASSE: é obtida através da diferença entre o limite superior e
inferior da classe e é simbolizada por hi = Li - li. Ex: na tabela anterior hi = 53 - 49 = 4. Obs: Na
distribuição de freqüência c/ classe o hi será igual em todas as classes.
AMPLITUDE TOTAL DA DISTRIBUIÇÃO: é a diferença entre o limite superior da última classe e o
limite inferior da primeira classe. AT = L(max) - l(min). Ex: na tabela anterior AT = 61 - 41= 20.
AMPLITUDE TOTAL DA AMOSTRA (ROL): é a diferença entre o valor máximo e o valor mínimo da
amostra (ROL). Onde AA = Xmax - Xmin. Em nosso exemplo AA = 60 - 41 = 19.

Obs: AT sempre será maior que AA.
PONTO MÉDIO DE CLASSE: é o ponto que divide o intervalo de classe em duas partes iguais. .......Ex:
em 49 |------- 53 o ponto médio x3 = (53+49)/2 = 51, ou seja x3=( l3 + L3 )/2.
Método prático para construção de uma Distribuição de Freqüências c/ Classe 
1º - Organize os dados brutos em um ROL.
2º - Calcule a amplitude amostral AA.
No nosso exmplo: AA = 60 - 41 = 19
3º - Calcule o número de classes através da "Regra de Sturges":
n
IIII
nº de classes
3 |-----| 5 3
6 |-----| 11 4
12 |-----| 22 5
23 |-----| 46 6
47 |-----| 90 7
91 |-----| 181 8
182 |-----| 362 9
Obs: Qualquer regra para determinação do nº de classes da tabela não nos levam a uma decisão final; esta
vai depender, na realidade de um julgamento pessoal, que deve estar ligado à natureza dos dados.
No nosso exemplo: n = 20 dados, então ,a princípio, a regra sugere a adoção de 5 classes.

4º - Decidido o nº de classes, calcule então a amplitude do intervalo de classe h > AA / i.
No nosso exemplo: AA/i = 19/5 = 3,8 . Obs: Como h > AA/i um valor ligeiramente superior para haver folga
na última classe. Utilizaremos então h = 4
5º - Temos então o menor nº da amostra, o nº de classes e a amplitude do intervalo. Podemos montar a
tabela, com o cuidado para não aparecer classes com freqüência = 0 (zero).
No nosso exemplo: o menor nº da amostra = 41 + h = 45, logo a primeira classe será representada por ...... 41
|------- 45. As classes seguintes respeitarão o mesmo procedimento.
O primeiro elemento das classes seguintes sempre serão formadas pelo último elemento da classe anterior.
REPRESENTAÇÃO GRÁFICA DE UMA DISTRIBUIÇÃO
Histograma, Polígono de freqüência e Polígono de freqüência acumulada
 Em todos os gráficos acima utilizamos o primeiro quadrante do sistema de eixos coordenados
cartesianos ortogonais. Na linha horizontal (eixo das abscissas) colocamos os valores da variável e na linha
vertical (eixo das ordenadas), as freqüências.
.
Histograma: é formado por um conjunto de retângulos justapostos, cujas bases se localizam sobre o eixo
horizontal, de tal modo que seus pontos médios coincidam com os pontos médios dos intervalos de classe. A
área de um histograma é proporcional à soma das freqüências simples ou absolutas.
Freqüências simples ou absoluta: são os valores que realmente representam o número de dados de cada
classe. A soma das freqüências simples é igual ao número total dos dados da distribuição.
Freqüências relativas: são os valores das razões entre as freqüência absolutas de cada classe e a
freqüência total da distribuição. A soma das freqüências relativas é igual a 1 (100 %).
.

Polígono de freqüência: é um gráfico em linha, sendo as freqüências marcadas sobre perpendiculares ao
eixo horizontal, levantadas pelos pontos médios dos intervalos de classe. Para realmente obtermos um
polígono (linha fechada), devemos completar a figura, ligando os extremos da linha obtida aos pontos
médios da classe anterior à primeira e da posterior à última, da distribuição.
.
Polígono de freqüência acumulada: é traçado marcando-se as freqüências acumuladas sobre
perpendiculares ao eixo horizontal, levantadas nos pontos correspondentes aos limites superiores dos
intervalos de classe.
Freqüência simples acumulada de uma classe: é o total das freqüências de todos os valores inferiores ao
limite superior do intervalo de uma determinada classe.
Freqüência relativa acumulada de um classe: é a freqüência acumulada da classe, dividida pela
freqüência total da distribuição.
...CLASSE.. ......fi..... .....xi..... .....fri..... .....Fi..... ......Fri.....
50 |-------- 54 4 52 0,100 4 0,100
54 |-------- 58 9 56 0,225 13 0,325
58 |-------- 62 11 60 0,275 24 0,600
62 |-------- 66 8 64 0,200 32 0,800
66 |-------- 70 5 68 0,125 37 0,925
70 |-------- 74 3 72 0,075 40 1,000
Total 40 1,000
fi = freqüência simples; xi = ponto médio de classe; fri = freqüência simples acumulada;
Fi = freqüência relativa e Fri = freqüência relativa acumulada.
• Obs: uma distribuição de freqüência sem intervalos de classe é representada graficamente por um
diagrama onde cada valor da variável é representado por um segmento de reta vertical e de
comprimento proporcional à respectiva freqüência.

.
3. MEDIDAS DE POSIÇÃO
Introdução
 São as estatísticas que representam uma série de dados orientando-nos quanto à posição da
distribuição em relação ao eixo horizontal do gráfico da curva de freqüência.
• As medidas de posições mais importantes são as medidas de tendência central ou promédias
(verifica-se uma tendência dos dados observados a se agruparem em torno dos valores centrais).
• As medidas de tendência central mais utilizadas são: média aritmética, moda e mediana. Outros
promédios menos usados são as médias: geométrica, harmônica, quadrática, cúbica e biquadrática.
• As outras medidas de posição são as separatrizes, que englobam: a própria mediana, os decis, os
quartis e os percentis.
.
MÉDIA ARITMÉTICA =
 É igual ao quociente entre a soma dos valores do conjunto e o número total dos valores.
......
onde xi são os valores da variável e n o número de valores.

.
Dados não-agrupados: Quando desejamos conhecer a média dos dados não-agrupados em tabelas de
freqüências, determinamos a média aritmética simples.
Ex: Sabendo-se que a venda diária de arroz tipo A, durante uma semana, foi de 10, 14, 13, 15, 16, 18 e
12 kilos, temos, para venda média diária na semana de:
.= (10+14+13+15+16+18+12) / 7 = 14 kilos
Desvio em relação à média: é a diferença entre cada elemento de um conjunto de valores e a média
aritmética, ou seja:.
. di = Xi -
No exemplo anterior temos sete desvios:... d1 = 10 - 14 = - 4 , ...d2 = 14 - 14 = 0 , d3 = 13 - 14 = - 1 , ...d4 =
15 - 14 = 1 ,... d5 = 16 - 14 = 2 ,... d6 = 18 - 14 = 4 ...e. .. d7 = 12 - 14 = - 2.
.
Propriedades da média aritmética 
1ª propriedade: A soma algébrica dos desvios em relação à média é nula.
• No exemplo anterior : d1+d2+d3+d4+d5+d6+d7 = 0

2ª propriedade: Somando-se (ou subtraindo-se) uma constante (c) a todos os valores de uma variável, a
média do conjunto fica aumentada ( ou diminuída) dessa constante.
• Se no exemplo original somarmos a constante 2 a cada um dos valores da variável temos:
Y = 12+16+15+17+18+20+14 / 7 = 16 kilos ou
Y = .+ 2 = 14 +2 = 16 kilos
3ª propriedade: Multiplicando-se (ou dividindo-se) todos os valores de uma variável por uma
constante (c), a média do conjunto fica multiplicada ( ou dividida) por essa constante.
• Se no exemplo original multiplicarmos a constante 3 a cada um dos valores da variável temos:
Y = 30+42+39+45+48+54+36 / 7 = 42 kilos ou
Y = x 3 = 14 x 3 = 42 kilos
.
Dados agrupados:
Sem intervalos de classe  Consideremos a distribuição relativa a 34 famílias de quatro filhos, tomando
para variável o número de filhos do sexo masculino. Calcularemos a quantidade média de meninos por
família:
Nº de meninos freqüência = fi

0 2
1 6
2 10
3 12
4 4
total 34
• Como as freqüências são números indicadores da intensidade de cada valor da variável, elas
funcionam como fatores de ponderação, o que nos leva a calcular a média aritmética ponderada,
dada pela fórmula:
..xi. ..fi. ..xi.fi .
0 2 0
1 6 6
2 10 20
3 12 36
4 4 16
total 34 78
onde 78 / 34 = 2,3 meninos por família
Com intervalos de classe  Neste caso, convencionamos que todos os valores incluídos em um
determinado intervalo de classe coincidem com o seu ponto médio, e determinamos a média aritmética
ponderada por meio da fórmula:
..
onde Xi é o ponto médio da classe.
Ex: Calcular a estatura média de bebês conforme a tabela abaixo.
Estaturas (cm) freqüência = fi ponto médio = xi ..xi.fi.

50 |------------ 54 4 52 208
54 |------------ 58 9 56 504
58 |------------ 62 11 60 660
62 |------------ 66 8 64 512
66 |------------ 70 5 68 340
70 |------------ 74 3 72 216
Total 40 2.440
Aplicando a fórmula acima temos: 2.440 / 40.= 61. logo... = 61 cm
Média Geométrica = g
 É a raiz n-ésima do produto de todos eles.
Média Geométrica Simples: ou .
Ex.: - Calcular a média geométrica dos seguintes conjuntos de números:E
a) { 10, 60, 360 }.: = ( 10 * 60 * 36 0) ^ (1/3) ....R: 60
b) { 2, 2, 2 }........: = (2 * 2 * 2 ^ (1/3) .. .R: 2
c) { 1, 4, 16, 64 }: = (1 * 4 * 16 * 64 ) ^(1/4) ....R: 8
.
Média Geométrica Ponderada :
ou ..
Ex - Calcular a média geométrica dos valores da tabela abaixo:

...xi... ...fi...
1 2
3 4
9 2
27 1
Total 9
= (12 * 34 * 92 * 271) (1/9)........R: 3,8296
.
MÉDIA HARMÔNICA - h
 É o inverso da média aritmética dos inversos.
.
Média Harmônica Simples:. (para dados não agrupados)
.. ou
.
Média Harmônica Ponderada : (para dados agrupados em tabelas de freqüências)
..

Ex.: Calcular a média harmônica dos valores da tabela abaixo:
classes ....fi.... ....xi.... ........fi/xi........
1 |--------- 3 2 2 2/2 = 1,00
3 |--------- 5 4 4 4/4 = 1,00
5 |--------- 7 8 6 8/6 = 1,33
7 |--------- 9 4 8 4/8 = 0,50
9 |--------- 11 2 10 2/10 = 0,20
total 20 4,03
Resp: 20 / 4,03 = 4,96
OBS: A média harmônica não aceita valores iguais a zero como dados de uma série.
• A igualdade g = h.= ....só ocorrerá quando todos os valores da série forem iguais.
OBS: Quando os valores da variável não forem muito diferentes, verifica-se aproximadamente a seguinte
relação:
g = ( .+ h ) /.2
• Demonstraremos a relação acima com os seguintes dados:
z = { 10,1 ; 10,1 ; 10,2 ; 10,4 ; 10,5 }
Média aritmética = 51,3 / 5 = 10,2600
Média geométrica= = 10,2587

Média harmônica = 5 / 0,4874508 = 10,2574
Comprovando a relação: 10,2600 + 10,2574 / 2 = 10,2587 = média geométrica
.
MODA - Mo
 É o valor que ocorre com maior freqüência em uma série de valores.
• Desse modo, o salário modal dos empregados de uma fábrica é o salário mais comum, isto é, o salário
recebido pelo maior número de empregados dessa fábrica.
.
A Moda quando os dados não estão agrupados 
• A moda é facilmente reconhecida: basta, de acordo com definição, procurar o valor que mais se
repete.
Ex: Na série { 7 , 8 , 9 , 10 , 10 , 10 , 11 , 12 } a moda é igual a 10.
• Há séries nas quais não exista valor modal, isto é, nas quais nenhum valor apareça mais vezes que
outros.
Ex: { 3 , 5 , 8 , 10 , 12 } não apresenta moda. A série é amodal.
• .Em outros casos, pode haver dois ou mais valores de concentração. Dizemos, então, que a série tem
dois ou mais valores modais.
Ex: { 2 , 3 , 4 , 4 , 4 , 5 , 6 , 7 , 7 , 7 , 8 , 9 } apresenta duas modas: 4 e 7. A série é bimodal.
.

A Moda quando os dados estão agrupados 
a) Sem intervalos de classe: Uma vez agrupados os dados, é possível determinar imediatamente a moda:
basta fixar o valor da variável de maior freqüência.
Ex: Qual a temperatura mais comum medida no mês abaixo:
Temperaturas Freqüência
0º C 3
1º C 9
2º C 12
3º C 6
Resp: 2º C é a temperatura modal, pois é a de maior freqüência.
.
b) Com intervalos de classe: A classe que apresenta a maior freqüência é denominada classe modal. Pela
definição, podemos afirmar que a moda, neste caso, é o valor dominante que está compreendido entre os
limites da classe modal. O método mais simples para o cálculo da moda consiste em tomar o ponto médio da
classe modal. Damos a esse valor a denominação de moda bruta.
Mo = ( l* + L* ) / 2
onde l* = limite inferior da classe modal e L* = limite superior da classe modal.
Ex: Calcule a estatura modal conforme a tabela abaixo.
Classes (em cm) Freqüência
54 |------------ 58 9
58 |------------ 62 11
62 |------------ 66 8
66 |------------ 70 5

Resposta: a classe modal é 58|-------- 62, pois é a de maior freqüência. l* = 58 e L* = 62
Mo = (58+62) / 2 = 60 cm ( este valor é estimado, pois não conhecemos o valor real da moda).
.
Método mais elaborado pela fórmula de CZUBER: Mo = l* + (d1/(d1+d2)) x h*
l* = limite inferior da classe modal..... e..... L* = limite superior da classe modal
d1 = freqüência da classe modal - freqüência da classe anterior à da classe modal
d2 = freqüência da classe modal - freqüência da classe posterior à da classe modal
h* = amplitude da classe modal
Mo = 58 + ((11-9) / ((11-9) + (11 – 8)) x 4  Mo = 59,6
Obs: A moda é utilizada quando desejamos obter uma medida rápida e aproximada de posição ou quando
a medida de posição deva ser o valor mais típico da distribuição. Já a média aritmética é a medida de posição
que possui a maior estabilidade.
MEDIANA - Md
 A mediana de um conjunto de valores, dispostos segundo uma ordem ( crescente ou decrescente), é o
valor situado de tal forma no conjunto que o separa em dois subconjuntos de mesmo número de elementos.
.
A mediana em dados não-agrupados 
Dada uma série de valores como, por exemplo: { 5, 2, 6, 13, 9, 15, 10 }

De acordo com a definição de mediana, o primeiro passo a ser dado é o da ordenação (crescente ou
decrescente) dos valores: { 2, 5, 6, 9, 10, 13, 15 }
O valor que divide a série acima em duas partes iguais é igual a 9, logo a Md = 9.
.
Método prático para o cálculo da Mediana:
 Se a série dada tiver número ímpar de termos: O valor mediano será o termo de ordem dado pela
fórmula :
.( n + 1 ) / 2
Ex: Calcule a mediana da série { 1, 3, 0, 0, 2, 4, 1, 2, 5 }
1º - ordenar a série { 0, 0, 1, 1, 2, 2, 3, 4, 5 }
n = 9 logo (n + 1)/2 é dado por (9+1) / 2 = 5, ou seja, o 5º elemento da série ordenada será a mediana
A mediana será o 5º elemento = 2
.
Se a série dada tiver número par de termos: O valor mediano será o termo de ordem dado pela
fórmula :....
.[( n/2 ) +( n/2+ 1 )] / 2
Obs: n/2 e (n/2 + 1) serão termos de ordem e devem ser substituídos pelo valor correspondente.
Ex: Calcule a mediana da série { 1, 3, 0, 0, 2, 4, 1, 3, 5, 6 }
1º - ordenar a série { 0, 0, 1, 1, 2, 3, 3, 4, 5, 6 }

n = 10 logo a fórmula ficará: [( 10/2 ) + (10/2 + 1)] / 2
[( 5 + 6)] / 2 será na realidade (5º termo+ 6º termo) / 2
5º termo = 2
6º termo = 3
A mediana será = (2+3) / 2 ou seja, Md = 2,5 . A mediana no exemplo será a média aritmética do 5º e 6º
termos da série.
Notas:
• Quando o número de elementos da série estatística for ímpar, haverá coincidência da mediana com
um dos elementos da série.
• Quando o número de elementos da série estatística for par, nunca haverá coincidência da mediana
com um dos elementos da série. A mediana será sempre a média aritmética dos 2 elementos centrais
da série.
• Em uma série a mediana, a média e a moda não têm, necessariamente, o mesmo valor.
• A mediana, depende da posição e não dos valores dos elementos na série ordenada. Essa é uma da
diferenças marcantes entre mediana e média ( que se deixa influenciar, e muito, pelos valores
extremos). Vejamos:
Em { 5, 7, 10, 13, 15 } a média = 10 e a mediana = 10
Em { 5, 7, 10, 13, 65 } a média = 20 e a mediana = 10
• isto é, a média do segundo conjunto de valores é maior do que a do primeiro, por influência dos
valores extremos, ao passo que a mediana permanece a mesma.
A mediana em dados agrupados 
a) Sem intervalos de classe: Neste caso, é o bastante identificar a freqüência acumulada imediatamente
superior à metade da soma das freqüências. A mediana será aquele valor da variável que corresponde a tal
freqüência acumulada.
Ex.: conforme tabela abaixo:

Variável xi Freqüência fi Freqüência acumulada
0 2 2
1 6 8
2 9 17
3 13 30
4 5 35
total 35
• Quando o somatório das freqüências for ímpar o valor mediano será o termo de ordem dado pela
fórmula :
.
• Como o somatório das freqüências = 35 a fórmula ficará: ( 35+1 ) / 2 = 18º termo = 3..
• Quando o somatório das freqüências for par o valor mediano será o termo de ordem dado pela
fórmula:
Ex: Calcule Mediana da tabela abaixo:
Variável xi Freqüência fi Freqüência acumulada
12 1 1
14 2 3
15 1 4
16 2 6
17 1 7

20 1 8
total 8
• Aplicando fórmula acima teremos:[(8/2)+ (8/2+1)]/2 = (4º termo + 5º termo) / 2 = (15 + 16) / 2 = 15,5
b) Com intervalos de classe: Devemos seguir os seguintes passos:
1º) Determinamos as freqüências acumuladas ;
2º) Calculamos ;
3º) Marcamos a classe correspondente à freqüência acumulada imediatamente superior à . Tal
classe será a classe mediana ;
4º) Calculamos a Mediana pela seguinte fórmula:. M Md = l* + [( - FAA ) x h*] / f*
l* = é o limite inferior da classe mediana.
FAA = é a freqüência acumulada da classe anterior à classe mediana.
f* = é a freqüência simples da classe mediana.
h* = é a amplitude do intervalo da classe mediana.
Ex:
classes freqüência = fi Freqüência acumulada
50 |------------ 54 4 4
54 |------------ 58 9 13
58 |------------ 62 11 24
62 |------------ 66 8 32
66 |------------ 70 5 37
70 |------------ 74 3 40
total 40

= 40 / 2 =.20........... logo.a classe mediana será 58 |---------- 62
l* = 58........... FAA = 13........... f* = 11........... h* = 4
Substituindo esses valores na fórmula, obtemos:
Md = 58 + [ (20 - 13) x 4] / 11 = 58 + 28/11 = 60,54
OBS: Esta mediana é estimada, pois não temos os 40 valores da distribuição.
Emprego da Mediana
• Quando desejamos obter o ponto que divide a distribuição em duas partes iguais.
• Quando há valores extremos que afetam de maneira acentuada a média aritmética.
• Quando a variável em estudo é salário.
SEPARATRIZES
 Além das medidas de posição que estudamos, há outras que, consideradas individualmente, não são
medidas de tendência central, mas estão ligadas à mediana relativamente à sua característica de separar a
série em duas partes que apresentam o mesmo número de valores.
Essas medidas - os quartis, os decis e os percentis - são, juntamente com a mediana, conhecidas pelo nome
genérico de separatrizes.
.
QUARTIS - Q
 Denominamos quartis os valores de uma série que a dividem em quatro partes iguais. Precisamos
portanto de 3 quartis (Q1 , Q2 e Q3) para dividir a série em quatro partes iguais.
Obs: O quartil 2 ( Q2 ) sempre será igual a mediana da série.

Quartis em dados não agrupados 
 O método mais prático é utilizar o princípio do cálculo da mediana para os 3 quartis. Na realidade
serão calculadas " 3 medianas " em uma mesma série.
Ex 1: Calcule os quartis da série: { 5, 2, 6, 9, 10, 13, 15 }
- O primeiro passo a ser dado é o da ordenação (crescente ou decrescente) dos valores: { 2, 5, 6, 9, 10, 13,
15 }
- O valor que divide a série acima em duas partes iguais é igual a 9, logo a Md = 9 que será = Q2 = 9
- Temos agora {2, 5, 6 } e {10, 13, 15 } como sendo os dois grupos de valores iguais proporcionados pela
mediana ( quartil 2 ). Para o cálculo do quartil 1 e 3 basta calcular as medianas das partes iguais
provenientes da verdadeira Mediana da série (quartil 2).
Logo em { 2, 5, 6 } a mediana é = 5 . Ou seja: será o quartil 1 = Q1 = 5
em {10, 13, 15 } a mediana é =13 . Ou seja: será o quartil 3 = Q = 13
Ex 2: Calcule os quartis da série: { 1, 1, 2, 3, 5, 5, 6, 7, 9, 9, 10, 13 }
- A série já está ordenada, então calcularemos o Quartil 2 = Md = (5+6)/2 = 5,5
-
- O quartil 1 será a mediana da série à esquerda de Md : { 1, 1, 2, 3, 5, 5 }
Q1 = (2+3)/2 = 2,5

- O quartil 3 será a mediana da série à direita de Md : {6, 7, 9, 9, 10, 13 }
Q3 = (9+9)/2 = 9
Quartis para dados agrupados em classes 
 Usamos a mesma técnica do cálculo da mediana, bastando substituir, na fórmula da mediana,
E fi / 2.... por ... k . E fi / 4 ... sendo k o número de ordem do quartil.
Assim, temos:
Q1 = . l* + [(E fi / 4 - FAA ) x h*] / f*
Q2 = . l* + [(2.E fi / 4 - FAA ) x h*] / f*
Q3 = . l* + [(3.E fi / 4 - FAA ) x h*] / f*
Ex 3 - Calcule os quartis da tabela abaixo:
classes freqüência = fi Freqüência acumulada
50 |------------ 54 4 4
54 |------------ 58 9 13
58 |------------ 62 11 24
62 |------------ 66 8 32
66 |------------ 70 5 37
70 |------------ 74 3 40
total 40

- O quartil 2 = Md , logo:
= 40 / 2 =.20........... logo.a classe mediana será 58 |---------- 62
l* = 58........... FAA = 13........... f* = 11........... h* = 4
Q2 = . l* + [(2.E fi / 4 - FAA ) x h*] / f*
- Substituindo esses valores na fórmula, obtemos:
Md = 58 + [ (20 - 13) x 4] / 11 = 58 + 28/11 = 60,54 = Q2
- O quartil 1 : E fi / 4 = 10
Q1 = . l* + [(E fi / 4 - FAA ) x h*] / f*
Q1 = 54 + [ (10 - 4) x 4] / 9 = 54 + 2,66 = 56,66 = Q1
.
- O quartil 3 : 3.E fi / 4 = 30
Q3 = . l* + [(3.E fi / 4 - FAA ) x h*] / f*
Q3 = 62 + [ (30 -24) x 4] / 8 = 62 + 3 = 65 = Q3
DECIS - D

 A definição dos decis obedece ao mesmo princípio dos quartis, com a modificação da porcentagem
de valores que ficam aquém e além do decil que se pretende calcular. A fórmula básica será : k .E fi / 10
onde k é o número de ordem do decil a ser calculado. Indicamos os decis : D1, D2, ... , D9. Deste modo
precisamos de 9 decis para dividirmos uma série em 10 partes iguais.
• De especial interesse é o quinto decil, que divide o conjunto em duas partes iguais. Assim sendo,o
quinto decil é igual ao segundo quartil, que por sua vez é igual à mediana.
Para D5 temos : 5.E fi / 10 = E fi / 2
Ex: Calcule o 3º decil da tabela anterior com classes.
k= 3 onde 3 .E fi / 10 = 3 x 40 / 10 = 12.
Este resultado corresponde a 2ª classe.
D3 = 54 + [ (12 - 4) x 4] / 9 = 54 + 3,55 = 57,55 = D3
PERCENTIL ou CENTIL
 Denominamos percentis ou centis como sendo os noventa e nove valores que separam uma série em
100 partes iguais. Indicamos: P1, P2, ... , P99. É evidente que P50 = Md ; P25 = Q1 e P75 = Q3.
• O cálculo de um centil segue a mesma técnica do cálculo da mediana, porém a fórmula será : k .E fi
/ 100 onde k é o número de ordem do centil a ser calculado.

Dispersão ou Variabilidade: É a maior ou menor diversificação dos valores de uma variável em torno de um
valor de tendência central ( média ou mediana ) tomado como ponto de comparação.
• A média - ainda que considerada como um número que tem a faculdade de representar uma série de
valores - não pode, por si mesma, destacar o grau de homogeneidade ou heterogeneidade que existe
entre os valores que compõem o conjunto.
• Consideremos os seguintes conjuntos de valores das variáveis X, Y e Z:
X = { 70, 70, 70, 70, 70 }
Y = { 68, 69, 70 ,71 ,72 }
Z = { 5, 15, 50, 120, 160 }
- Observamos então que os três conjuntos apresentam a mesma média aritmética = 350/5 = 70
• Entretanto, é fácil notar que o conjunto X é mais homogêneo que os conjuntos Y e Z, já que todos os
valores são iguais à média. O conjunto Y, por sua vez, é mais homogêneo que o conjunto Z, pois há
menor diversificação entre cada um de seus valores e a média representativa.
• Concluímos então que o conjunto X apresenta dispersão nula e que o conjunto Y apresenta uma
dispersão menor que o conjunto Z.
MEDIDAS DE DISPERSÃO ABSOLUTA
Amplitude total: É a única medida de dispersão que não tem na média o ponto de referência.
• Quando os dados não estão agrupados a amplitude total é a diferença entrE o maior e o menor valor
observado:

AT = X máximo - X mínimo.
Ex: Para os valores 40, 45, 48, 62 e 70 a amplitude total será: AT = 70 - 40 = 30
Quando os dados estão agrupados sem intervalos de classe ainda temos :
AT = X máximo - X mínimo.
Ex:
xi fi
0 2
1 6
3 5
4 3
AT = 4 - 0 = 4
* Com intervalos de classe a amplitude total é a diferença entre o limite superior da última classe e o limite
inferior da primeira classe. Então:
AT = L máximo - l mínimo
Ex:
Classes fi
4 |------------- 6 6
6 |------------- 8 2
8 |------------- 10 3
AT = 10 - 4 = 6
• A amplitude total tem o inconveniente de só levar em conta os dois valores extremos da série,
descuidando do conjunto de valores intermediários. Faz-se uso da amplitude total quando se quer

determinar a amplitude da temperatura em um dia, no controle de qualidade ou como uma medida
de cálculo rápido sem muita exatidão.
Desvio quartil: Também chamado de amplitude semi-interquatílica e é baseada nos quartis.
Símbolo: Dq e a Fórmula: Dq = (Q3 - Q1) / 2
Observações:
1 - O desvio quartil apresenta como vantagem o fato de ser uma medida fácil de calcular e de
interpretar. Além do mais, não é afetado pelos valores extremos, grandes ou pequenos, sendo recomendado,
por conseguinte, quando entre os dados figurem valores extremos que não se consideram representativos.
2- O desvio quartil deverá ser usado preferencialmente quando a medida de tendência central for a
mediana.
3- Trata-se de uma medida insensível ã distribuição dos itens menores que Q1, entre Q1 e Q3 e maiores
que Q3.
Ex: Para os valores 40, 45, 48, 62 e 70 o desvio quartil será:
Q1 = (45+40)/2 = 42,5 Q3 = (70+62)/2 = 66 Dq = (66 - 42,5) / 2 = 11,75
Desvio médio absoluto - Dm
Para dados brutos: É a média aritmética dos valores absolutos dos desvios tomados em relação a uma das
seguintes medidas de tendência central: média ou mediana.

• para a Média = Dm = E | Xi - | / n
• para a Mediana = Dm = E | Xi - Md | / n
• As barras verticais indicam que são tomados os valores absolutos, prescindindo do sinal dos desvios.
Ex: Calcular o desvio médio do conjunto de números { - 4 , - 3 , - 2 , 3 , 5 }
= - 0, 2 e Md = - 2
Tabela auxiliar para cálculo do desvio médio
Xi Xi - | Xi - | Xi - Md | Xi - Md |
- 4 (- 4) - (-0,2) = -3,8 3,8 (- 4) - (-2) = - 2 2
- 3 (- 3) - (-0,2) = -2,8 2,8 (- 3) - (-2) = - 1 1
- 2 (- 2) - (-0,2) = -1,8 1,8 (- 2) - (-2) = 0 0
3 3 - (-0,2) = 3,2 3,2 3 - (-2) = 5 5
5 5 - (-0,2) = 5,2 5,2 5 - (-2) = 7 7
E = 16,8 E = 15
Pela Média : Dm = 16,8 / 5 = 3,36 Pela Mediana : Dm = 15 / 5 = 3

DESVIO PADRÃO - S
 É a medida de dispersão mais geralmente empregada, pois leva em consideração a totalidade dos
valores da variável em estudo. É um indicador de variabilidade bastante estável. O desvio padrão baseia-se
nos desvios em torno da média aritmética e a sua fórmula básica pode ser traduzida como : a raiz quadrada
da média aritmética dos quadrados dos desvios e é representada por S .
• A fórmula acima é empregada quando tratamos de uma população de dados não-agrupados.
Ex: Calcular o desvio padrão da população representada por - 4 , -3 , -2 , 3 , 5
Xi
- 4 - 0,2 - 3,8 14,44
- 3 - 0,2 - 2,8 7,84
- 2 - 0,2 - 1,8 3,24
3 - 0,2 3,2 10,24
5 - 0,2 5,2 27,04
E = 62,8
Sabemos que n = 5 e 62,8 / 5 = 12,56.
A raiz quadrada de 12,56 é o desvio padrão = 3,54

Obs: Quando nosso interesse não se restringe à descrição dos dados mas, partindo da amostra, visamos
tirar inferências válidas para a respectiva população, convém efetuar uma modificação, que consiste em usar
o divisor n - 1 em lugar de n. A fórmula ficará então:
• Se os dados - 4 , -3 , -2 , 3 , 5 representassem uma amostra o desvio padrão amostral seria a raiz
quadrada de 62,8 / (5 -1) = 3,96
• O desvio padrão goza de algumas propriedades, dentre as quais destacamos:
1ª = Somando-se (ou subtraindo-se) uma constante a todos os valores de uma variável, o desvio padrão
não se altera.
2ª = Multiplicando-se (ou dividindo-se) todos os valores de uma variável por uma constante (diferente de
zero), o desvio padrão fica multiplicado ( ou dividido) por essa constante.
• Quando os dados estão agrupados (temos a presença de freqüências) a fórmula do desvio padrão
ficará :
ou quando se trata de uma amostra
Ex: Calcule o desvio padrão populacional da tabela abaixo:

Xi f i Xi . f i . f i
0 2 0 2,1 -2,1 4,41 8,82
1 6 6 2,1 -1,1 1,21 7,26
2 12 24 2,1 -0,1 0,01 0,12
3 7 21 2,1 0,9 0,81 5,67
4 3 12 2,1 1,9 3,61 10,83
Total 30 63 E = 32,70
- Sabemos que E fi = 30 e 32,7 / 30 = 1,09.
- A raiz quadrada de 1,09 é o desvio padrão = 1,044
- Se considerarmos os dados como sendo de uma amostra o desvio padrão seria : a raiz quadrada de 32,7 /
(30 -1) = 1,062
Obs: Nas tabelas de freqüências com intervalos de classe a fórmula a ser utilizada é a mesma do exemplo
anterior.
VARIÂNCIA - S2
 É o desvio padrão elevado ao quadrado. A variância é uma medida que tem pouca utilidade como
estatística descritiva, porém é extremamente importante na inferência estatística e em combinações de
amostras.
MEDIDAS DE DISPERSÃO RELATIVA
Coeficiente de Variação de Pearson - CVP

Na estatística descritiva o desvio padrão por si só tem grandes limitações. Assim, um desvio padrão
de 2 unidades pode ser considerado pequeno para uma série de valores cujo valor médio é 200; no
entanto, se a média for igual a 20, o mesmo não pode ser dito.
Além disso, o fato de o desvio padrão ser expresso na mesma unidade dos dados limita o seu emprego
quando desejamos comparar duas ou mais séries de valores, relativamente à sua dispersão ou
variabilidade, quando expressas em unidades diferentes.
Para contornar essas dificuldades e limitações, podemos caracterizar a dispersão ou variabilidade dos
dados em termos relativos a seu valor médio, medida essa denominada de CVP: Coeficiente de
Variação de Pearson (é a razão entre o desvio padRão e a média referentes a dados de uma mesma
série).
CVP = (S / ) x 100
o resultado neste caso é expresso em percentual, entretanto pode ser expresso também
através de um fator decimal, desprezando assim o valor 100 da fórmula.
Ex: Tomemos os resultados das estaturas e dos pesos de um mesmo grupo de indivíduos:
Discriminação M É D I A DESVIO PADRÃO
ESTATURAS 175 cm 5,0 cm
PESOS 68 kg 2,0 kg
- Qual das medidas (Estatura ou Peso) possui maior homogeneidade ?
Resposta: Teremos que calcular o CVP da Estatura e o CVP do Peso. O resultado menor será o de maior
homogeneidade ( menor dispersão ou variabilidade).
CVP estatura = ( 5 / 175 ) x 100 = 2,85 %

CVP peso = ( 2 / 68 ) x 100 = 2,94 %.
Logo, nesse grupo de indivíduos, as estaturas apresentam menor grau de dispersão que os pesos.
Coeficiente de Variação de Thorndike - CVT
É igual ao quociente entre o desvio padrão e a mediana.
CVT = ( S / Md ) x 100 %
Coeficiente Quartílico de Variação - CVQ
Esse coeficiente é definido pela seguinte expressão:
CVQ = [(Q3 - Q1) / (Q3 + Q1)] x 100 %.
Desvio quartil Reduzido – Dqr
Dqr = [(Q3 - Q1) / 2Md ] x 100 %.

5. MEDIDAS DE ASSIMETRIA
Introdução:
Uma distribuição com classes é simétrica quando :
Média = Mediana = Moda
 Uma distribuição com classes é :
Assimétrica à esquerda ou negativa quando : Média < Mediana < Moda
Assimétrica à direita ou positiva quando : Média > Mediana > Moda
Coeficiente de assimetria: A medida anterior, por ser absoluta, apresenta a mesma deficiência do desvio
padrão, isto é, não permite a possibilidade de comparação entre as medidas de duas distribuições. Por esse
motivo, daremos preferência ao coeficiente de assimetria de Person:
As = 3 ( Média - Mediana ) / Desvio Padrão
Escalas de assimetria:
| AS | < 0,15  assimetria pequena
0,15 < | AS | < 1  assimetria moderada

| AS | > 1  assimetria elevada
Obs: Suponhamos AS = - 0,49  a assimetria é considerada moderada e negativa
Suponhamos AS = 0,75  a assimetria é considerada moderada e positiva
MEDIDAS DE CURTOSE
Introdução:
Denominamos curtose o grau de achatamento de uma distribuição em relação a uma distribuição
padrão, denominada curva normal (curva correspondente a uma distribuição teórica de
probabilidade).
Quando a distribuição apresenta uma curva de freqüência mais fechada que a normal (ou mais aguda
ou afilada em sua parte superior), ela recebe o nome de leptocúrtica.
Quando a distribuição apresenta uma curva de freqüência mais aberta que a normal (ou mais
achatada em sua parte superior), ela recebe o nome de platicúrtica.
 A curva normal, que é a nossa base referencial, recebe o nome de mesocúrtica.
Coeficiente de curtose
C1 = (Q3 - Q1) / 2(P90 - P10)

• Este coeficiente é conhecido como percentílico de curtose.
• Relativamente a curva normal, temos:
C1 = 0,263  curva mesocúrtica
C1 < 0,263  curva leptocúrtica
C1 > 0,263  curva platicúrtica
O coeficiente abaixo ( C2 )será utilizado em nossas análises:
onde S é desvio padrão
C2 = 3  curva mesocúrtica
C2 > 3  curva leptocúrtica
C2 < 3  curva platicúrtica
Matemática Financeira

A Matemática Financeira é uma ferramenta útil na análise de algumas alternativas de investimentos ou
financiamentos de bens de consumo. A idéia básica é simplificar a operação financeira a um Fluxo de Caixa
e empregar alguns procedimentos matemáticos.
Capital: O Capital é o valor aplicado através de alguma operação financeira. Também conhecido como:
Principal, Valor Atual, Valor Presente ou Valor Aplicado. Em língua inglesa, usa-se Present Value, indicado
nas calculadoras financeiras pela tecla PV.
Juros: Juros representam a remuneração do Capital empregado em alguma atividade produtiva. Os juros
podem ser capitalizados segundo os regimes: simples ou compostos, ou até mesmo, com algumas condições
mistas.
RegimeRegimeRegimeRegime Processo de funcionamentoProcesso de funcionamentoProcesso de funcionamentoProcesso de funcionamento
SimplesSimplesSimplesSimples Somente o principal rende juros.
CompostosCompostosCompostosCompostos
Após cada período, os juros são incorporados ao Capital,
proporcionando juros sobre juros.
Notações comuns que serão utilizadas neste material
CCCC Capital
nnnn número de períodos
jjjj juros simples decorridos n períodos
JJJJ juros compostos decorridos n períodos
rrrr taxa percentual de juros
iiii taxa unitária de juros (i = r / 100)
PPPP Principal ou valor atual
MMMM Montante de capitalização simples
SSSS Montante de capitalização composta
Compatibilidade dos dados
Se a taxa de juros for mensal, trimestral ou anual, os períodos deverão ser respectivamente, mensais,
trimestrais ou anuais, de modo que os conceitos de taxas de juros e períodos sejam compatíveis, coerentes
ou homogêneos. Situações onde isto não ocorre, serão estudadas à parte e deverão ser feitas conversões de
unidades.
Exemplo: Na fórmula
F(i,n) = 1 + i n
a taxa unitária de juros i deverá estar indicada na mesma unidade de tempo que o número de períodos n, ou
seja, se a taxa é i=0,05 ao mês, então n deverá ser um número indicado em meses.
Juros simples

1. Se n é o numero de períodos, i é a taxa unitária ao período e P é o valor principal, então os juros
simples são calculados por:
j = P i n
Exemplo: Os juros simples obtidos por um capital P=1.250,00 durante 4 anos à taxa de 14% ao ano
são dados por:
j = 1.250,00 x 0,14 x 4 = 700,00
2. Se a taxa ao período é indicada percentualmente, substituímos i por r/100 e obtemos a fórmula:
j = P r n / 100
Exemplo: Os juros simples obtidos por um capital P=1.250,00 durante 4 anos à taxa de 14% ao ano
são dados por:
j = 1.250,00 x 14 x 4 / 100 = 700,00
3. Se a taxa é r % ao mês, usamos m como o número de meses e a fórmula:
j = P r m / 100
Exemplo: Os juros simples obtidos por um capital P=1.250,00 durante 4 anos (48 meses) à taxa de 2%
ao mês são dados por:
j = 1.250,00 x 2 x 48 / 100 = 1.200,00
4. Se a taxa é r% ao dia, usamos d como o número de dias para obter os juros exatos (número exato de
dias) ou comerciais simples com a fórmula:
j = P r d / 100
Exemplo: Os juros simples obtidos por um capital P=1.250,00 durante 6 meses (180 dias) à taxa de
0,02% ao dia são dados por:
j = 1.250,00 x 0,02 x 180 / 100 = 45,00
Exemplo: Os juros simples exatos obtidos por um capital P=1.250,00 durante os 6 primeiros meses do
ano de 1999 (181 dias), à taxa de 0,2% ao dia, são dados por:
j = 1.250,00 x 0,2 x 181 / 100 = 452,50
Montante simples
Montante é a soma do Capital com os juros. O montante também é conhecido como Valor Futuro. Em
língua inglesa, usa-se Future Value, indicado nas calculadoras financeiras pela tecla FV. O montante é dado
por uma das fórmulas:
M = P + j = P (1 + i n)
Exemplo a: Se a taxa de uma aplicação é de 150% ao ano, quantos meses serão necessários para dobrar um
capital aplicado através de capitalização simples?
Objetivo: M=2P
Dados: i=150/100=1,5; Fórmula: M=P(1+in)
Desenvolvimento: Como 2P=P(1+1,5 n), então 2=1+1,5 n, logo

n = 2/3 ano = 8 meses
Exemplo b: Qual é o valor dos juros simples pagos à taxa i=100% ao ano se o valor principal é P=R$ 1.000,00
e a dívida foi contraída no dia 10 de janeiro, sendo que deverá ser paga no dia 12 de abril do mesmo ano?
Contagem do tempo:
PeríodoPeríodoPeríodoPeríodo Número de diasNúmero de diasNúmero de diasNúmero de dias
De 10/01 até 31/01De 10/01 até 31/01De 10/01 até 31/01De 10/01 até 31/01 21 dias21 dias21 dias21 dias
TotalTotalTotalTotal 92 dias92 dias92 dias92 dias
Fórmula para o cálculo dos juros exatos:
j = P r (d / 365) / 100
Cálculo:
j = (1000×100×92/365)/100 = 252,05
Fluxo de caixa
Apresentaremos aqui, apenas alguns elementos sobre fluxo de caixa.
Fluxo de Caixa é um gráfico contendo informações sobre Entradas e Saídas de capital, realizadas em
determinados períodos. O fluxo de caixa pode ser apresentado na forma de uma linha horizontal (linha de
tempo) com os valores indicados nos respectivos tempos ou na forma de uma tabela com estas mesmas
indicações.
A entrada de dinheiro para um caixa em um sistema bancário poderá ser indicada por uma seta para baixo
enquanto que o indivíduo que pagou a conta deverá colocar uma seta para cima. A inversão das setas é uma
coisa comum e pode ser realizada sem problema.
Consideremos uma situação em que foi feito um depósito inicial de R$5.000,00 em uma conta que rende
juros de 4% ao ano, compostos mensalmente e que se continue a depositar mensalmente valores de
R$1.000,00 durante os 5 meses seguintes. No 6º. mês quer-se conhecer o Valor Futuro da reunião destes
depósitos.

Para obter o Valor Futuro deste capital depositado em vários meses, usamos o fluxo de caixa e conceitos
matemáticos para calcular o valor resultante ou montante acumulado.
Juros compostos
Em juros compostos, o problema principal consiste em calcular o montante (soma) S obtido pela aplicação
de um único valor principal P no instante t=0, à taxa i de juros (por período) durante n períodos.
Exemplo preparatório: Consideremos uma situação hipotética que, em 1994 a correção da caderneta de
poupança tenha sido de 50% em cada um dos 5 primeiros meses do ano. Se uma pessoa depositou $100,00
em 01/01/94, poderiamos montar uma tabela para obter o resultado acumulado em 01/06/94.
TempoTempoTempoTempo DataDataDataData Valor PrincipalValor PrincipalValor PrincipalValor Principal JurosJurosJurosJuros MontanteMontanteMontanteMontante
0000 01/01/9401/01/9401/01/9401/01/94 100,00100,00100,00100,00 0000 100,00100,00100,00100,00
1111 01/02/9401/02/9401/02/9401/02/94 100,00100,00100,00100,00 50,0050,0050,0050,00 150,00150,00150,00150,00
2222 01/03/9401/03/9401/03/9401/03/94 150,00150,00150,00150,00 75,0075,0075,0075,00 225,00225,00225,00225,00
3333 01/04/9401/04/9401/04/9401/04/94 225,00225,00225,00225,00 112,50112,50112,50112,50 337,50337,50337,50337,50
4444 01/05/9401/05/9401/05/9401/05/94 337,50337,50337,50337,50 168,75168,75168,75168,75 506,20506,20506,20506,20
5555 01/06/9401/06/9401/06/9401/06/94 506,25506,25506,25506,25 253,13253,13253,13253,13 759,38759,38759,38759,38
Observamos que os juros foram calculados sobre os Principais nos inícios dos meses que correspondiam aos
montantes dos finais dos meses anteriores.
Juros Compostos são juros sobre juros (anatocismo)
A situação apresentada acima, pode ser analisada do ponto de vista matemático, com P=100,00 e i=50%=0,5.
Assim:
S1=100(1,5)1S1=100(1,5)1S1=100(1,5)1S1=100(1,5)1 S2=100(1,5)2S2=100(1,5)2S2=100(1,5)2S2=100(1,5)2 S3=100(1,5)3S3=100(1,5)3S3=100(1,5)3S3=100(1,5)3 S4=100(1,5)4S4=100(1,5)4S4=100(1,5)4S4=100(1,5)4 S5=100(1,5)5S5=100(1,5)5S5=100(1,5)5S5=100(1,5)5
Em geral:
Sn = P (1+i)n
onde
SnSnSnSn Soma ou montante
PPPP Valor Principal aplicado inicialmente
iiii taxa unitária
nnnn número de períodos da aplicação
Observação: Relembramos que a taxa e o número de períodos devem ser compatíveis ou homogêneos com
respeito à unidade de tempo.
Montante composto
A fórmula para o cálculo do Montante, em função do valor Principal P, da taxa i ao período e do número de
períodos n, é dada por:

S = P (1+i)n
Exemplo: Se a taxa de uma aplicação é de 150% ao ano, quanto tempo será necessário para dobrar o capital
aplicado através de capitalização composta?
Objetivo: S=2P
Taxa anual: i=150/100=1,5. A fórmula é dada por:
S=P(1+i)n
Solução: 2P=P(1+1,5)n, logo
(2,5)n = 2
Para resolver esta última equação, aplicamos logaritmos a ambos os lados da igualdade, para obter:
n = log(2) / log(2,5) = 0,7564708 de 1 ano
Observação: Tábua de logaritmo imediata
Fator de Acumulação de Capital (Fator de P para S)
Se i é a taxa ao período, n é o número de períodos, definimos o Fator de Acumulação de Capital ou Fator de
P para S, denotado por FAC(i,n) ou FPS(i,n), como:
FAC(i,n) = FPS(i,n) = (1 + i)n
Agora, podemos escrever o montante composto S como o produto do valor Principal P por FAC(i,n):
S = P FAC(i,n) = P FPS(i,n)
Utilidade: O FAC(i,n)=(1+i)n pode ser obtido com uma calculadora simples, dessas que normalmente não
executam potências. Digita-se i, soma-se 1, aperta-se o sinal X (de multiplicação) e a seguir tecla-se o sinal
de igualdade n-1 vezes.
Existem algumas variações da fórmula do Montante Composto, que estão apresentadas abaixo:
S = P (1 + i)nS = P (1 + i)nS = P (1 + i)nS = P (1 + i)n
P = S (1+i)-nP = S (1+i)-nP = S (1+i)-nP = S (1+i)-n
Uma variação da fórmula de Montante composto é usada na obtenção do Valor Atual P de um capital futuro
conhecido S.
P=S(1+i)-n

Fator de Valor Atual
Se i é a taxa ao período, n é o número de períodos, o Fator de Valor Atual ou Fator de S para P ou Fator de
Desconto, denotado por FVA(i,n) ou FSP(i,n) como o inverso de FAC(i,n)=FPS(i,n):
FVA(i,n) = FSP(i,n) = (1+i)-n
Utilidade: O FVA(i,n)=(1+i)-n pode ser obtido com uma calculadora simples, dessas que normalmente não
executam potências. Digita-se i, soma-se 1, aperta-se o sinal X (de multiplicação) e o sinal = (igual) n-1
vezes para obter FAC(i,n) e a seguir teclamos o sinal de divisão e finalmente o sinal = (igual) para obter o
FVA(i,n), que é o inverso do FAC(i,n).
Cálculo de juros Compostos
J = P [(1+i)n-1]
Exemplo: Qual é o valor dos juros compostos pagos à taxa i=100% ao ano se o Principal é R$1.000,00 e a
dívida foi contraída no dia 10/01/94 e deverá ser paga em 12/04/94?
Solução: A contagem dos dias corresponde a d=92 dias.
Dúvida: Qual será a fórmula para juros compostos quando a taxa é anual e o período está indicado em uma
unidade diferente de 1 ano? A idéia é transformar 92 dias em unidades anuais para obter:
n = 92/365 de 1 ano = ~ 0,252055 = 1/4 ano
Principal: P=1000; Taxa anual: i=100/100=1. A fórmula empregada é:
J = P [(1+i)n-1]
Solução:
J=1000[(1+1)1/4-1]=1000(1,189207-1)=189,21
Teste: Você saberia obter a raiz quarta de um número com uma calculadora que só extrai a raiz quadrada? E
a raiz oitava de um número que só extrai a raiz quadrada?
Taxas
Taxa é um índice numérico relativo cobrado sobre um capital para a realização de alguma operação
financeira.
Taxas: (Matemática Financeira, Introdução ao Cap.6, José Dutra Vieira Sobrinho: "No mercado financeiro
brasileiro, mesmo entre os técnicos e executivos, reina muita confusão quanto aos conceitos de taxas de
juros principalmente no que se refere às taxas nominal, efetiva e real. O desconhecimento generalizado
desses conceitos tem dificultado o fechamento de negócios pela consequente falta de entendimento entre as
partes. Dentro dos programas dos diversos cursos de Matemática Financeira existe uma verdadeira
'poluição' de taxas de juros."
Não importando se a capitalização é simples ou composta, existem três tipos principais de taxas:

Taxa Nominal: A taxa Nominal é quando o período de formação e incorporação dos juros ao Capital não
coincide com aquele a que a taxa está referida.
Exemplos:
1. 1200% ao ano com capitalização mensal.
2. 450% ao semestre com capitalização mensal.
3. 300% ao ano com capitalização trimestral.
Taxa Efetiva: A taxa Efetiva é quando o período de formação e incorporação dos juros ao Capital coincide
com aquele a que a taxa está referida.
Exemplos:
1. 120% ao mês com capitalização mensal.
2. 450% ao semestre com capitalização semestral.
3. 1300% ao ano com capitalização anual.
Taxa Real: Taxa Real é a taxa efetiva corrigida pela taxa inflacionária do período da operação.
Conexão entre as taxas real, efetiva e de inflação: A taxa Real não é a diferença entre a taxa efetiva e a taxa
da inflação. Na realidade, existe uma ligação íntima entre as três taxas, dadas por:
1+iefetiva = (1+ireal) (1+iinflação)
Exemplo: Se a taxa de inflação mensal foi de 30% e um valor aplicado no início do mês produziu um
rendimento global de 32,6% sobre o valor aplicado, então o resultado é igual a 1,326 sobre cada 1 unidade
monetária aplicada. Assim, a variação real no final deste mês, será definida por:
vreal = 1 + ireal
que pode ser calculada por:
vreal = resultado / (1 + iinflação)
isto é:
vreal = 1,326 / 1,3 = 1,02
o que significa que a taxa real no período, foi de:
ireal = 2%
Aplicação em caderneta de poupança: Se o governo anuncia que a Caderneta de Poupança proporciona um
rendimento real de 0,5% ao mês (=0,005), significa que o seu dinheiro deve ser corrigido pela taxa da
inflação iinflação, isto é, deve ser multiplicado por 1 + iinflação e depois multiplicado por 1+0,5%=1,005.
Exemplo: Se uma pessoa possuia numa caderneta de poupança o valor de CR$ 670.890,45 no dia 30/04/93 e
a taxa da inflação desde esta data até 30/05/93 foi de 35,64% entao ele terá em sua conta no dia 30/05/93, o

valor de:
V = 670.890,45 x 1,3564 x 1,005 = 914.545,77
Taxas equivalentes
Duas taxas i1 e i2 são equivalentes, se aplicadas ao mesmo Capital P durante o mesmo período de tempo,
através de diferentes sistemas de capitalização, produzem o mesmo montante final.
Exemplo: A aplicação de R$1.000,00 à taxa de 10% ao mês durante 3 meses equivale a uma única aplicação
com a taxa de 33,1% ao trimestre. Observemos o Fluxo de caixa da situação.
Tomando P=1.000,00; i1=0,1 ao mês e n1=3 meses, seguirá pela fórmula do Montante composto, que :
S1=P(1+i1)3=1000(1+0,1)3=1000.(1,1)3=1331,00
Tomando P=1.000,00; i2=33,1% ao trimestre e n2=1 trimestre e usando a fórmula do Montante composto,
teremos:
S2=C(1+i2)1=1000(1+0,331)=1331,00
Logo S1=S2 e a taxa de 33,1% ao trimestre é equivalente à taxa capitalizada de 10% ao mês no mesmo
trimestre.
Observação sobre taxas equivalentes: Ao afirmar que a taxa nominal de uma aplicação é de 300% ao ano
capitalizada mensalmente, estamos entendemos que a taxa é de 25% ao mês e que está sendo aplicada mês a
mês, porque:
i = 300/12 = 25
Analogamente, temos que a taxa nominal de 300% ao ano corresponde a uma taxa de 75% ao trimestre,
aplicada a cada trimestre, porque:
i = 300/4 = 75
É evidente que estas taxas não são taxas efetivas.
Cálculos de taxas equivalentes: Como vimos, taxas equivalentes são aquelas obtidas por diferentes processos
de capitalização de um mesmo Principal P para obter um mesmo montante S.
Consideraremos ia uma taxa ao ano e ip uma taxa ao período p, sendo que este período poderá ser: 1
semestre, 1 quadrimestre, 1 trimestre, 1 mês, 1 quinzena, 1 dia ou outro que se deseje. Deve ficar claro que
tomamos 1 ano como o período integral e que o número de vezes que cada período parcial ocorre em 1 ano
é indicado por Np.
Exemplo: 1 ano = 2 semestres = 3 quadrimestres = 4 trimestres = 12 meses = 24 quinzenas = 360 dias.
A fórmula básica que fornece a equivalência entre duas taxas é:
1 + ia = (1+ip)Np

onde
iaiaiaia taxa anual
ipipipip taxa ao período
NpNpNpNp número de vezes em 1 ano
Situações possíveis com taxas equivalentes
FórmulaFórmulaFórmulaFórmula TaxaTaxaTaxaTaxa PeríodoPeríodoPeríodoPeríodo Número de vezesNúmero de vezesNúmero de vezesNúmero de vezes
1+ia = (1+isem)21+ia = (1+isem)21+ia = (1+isem)21+ia = (1+isem)2 isemisemisemisem semestresemestresemestresemestre 2222
1+ia = (1+iquad)31+ia = (1+iquad)31+ia = (1+iquad)31+ia = (1+iquad)3 iquadiquadiquadiquad quadrimestrequadrimestrequadrimestrequadrimestre 3333
1+ia = (1+itrim)41+ia = (1+itrim)41+ia = (1+itrim)41+ia = (1+itrim)4 itrimitrimitrimitrim trimestretrimestretrimestretrimestre 4444
1+ia = (1+imes)121+ia = (1+imes)121+ia = (1+imes)121+ia = (1+imes)12 imesimesimesimes mêsmêsmêsmês 12121212
1+ia = (1+iquinz)241+ia = (1+iquinz)241+ia = (1+iquinz)241+ia = (1+iquinz)24 iquinziquinziquinziquinz quinzenaquinzenaquinzenaquinzena 24242424
1+ia =1+ia =1+ia =1+ia =
(1+isemana)24(1+isemana)24(1+isemana)24(1+isemana)24
isemanisemanisemaniseman
aaaa
semanasemanasemanasemana 52525252
1+ia = (1+idias)3651+ia = (1+idias)3651+ia = (1+idias)3651+ia = (1+idias)365 idiasidiasidiasidias diadiadiadia 365365365365
Exemplo: Qual será a taxa efetiva que equivale à taxa de 12% ao ano capitalizada mês a mês?
Vamos entender a frase: "12% ao ano capitalizada mês a mês". Ela significa que devemos dividir 12% por 12
meses para obter a taxa que é aplicada a cada 1 mês. Se estivesse escrito "12% ao ano capitalizada
trimestralmente" deveriamos entender que a taxa ao trimestre seria igual a 12% dividido por 4 (número de
trimestres de 1 ano) que é 3%.
Vamos observar o fluxo de caixa da situação:
Solução: A taxa mensal é i1=12%/12=1%=0,01, assim a taxa efetiva pode ser obtida por
1+i2 = (1,01)12 = 1,1268247
logo
i2 = 0,1268247 = 12,68247%
Observação: Se iinflação=0, a taxa real equivale à taxa efetiva.
Exemplo: Qual é a taxa mensal efetiva que equivale à taxa de 12% ao ano? Neste caso, a fórmula a ser usada
é:
1+ia = (1 + imes)12
Como ia=12%=0,12 basta obter i(mes) com a substituição dos valores na fórmula acima para obter:
1,12 = [1 + i(mes)]12
Existem outras maneiras para resolver esta equação exponencial mas aplicaremos o logaritmo na base 10 a
ambos os lados da igualdade para obter:

log(1,12) = 12 log[1+i(mes)]
log(1,12)/12 = log[1 + i(mes)]
0,04921802267018/12 = log[1 + i(mes)]
0,004101501889182 = log[1+i(mes)]
assim
100,004101501889182 = 10log[1+i(mes)]
Desenvolvendo a potência obtemos:
1,009488792934 = 1 + i(mes)
0,009488792934 = i(mes)
i(mes) = 0,9488792934%
Observação: Interprete os últimos exemplos com muito cuidado!
Descontos
Notações comuns na área de descontos:
DDDD Desconto realizado sobre o título
AAAA Valor Atual de um título
NNNN Valor Nominal de um título
iiii Taxa de desconto
nnnn Número de períodos para o desconto
Desconto é a diferença entre o Valor Nominal de um título (futuro) N e o Valor Atual A deste mesmo
título.
D = N - A
Há dois tipos básicos de descontos: Comerciais (por fora) ou Racionais (por dentro).
Tipos de descontos
Descontos simples são obtidos com cálculos lineares, mas os Descontos compostos são obtidos com cálculos
exponenciais.
Desconto Simples Comercial (por fora): O cálculo deste desconto é análogo ao cálculo dos juros simples,
substituindo-se o Capital P na fórmula de juros simples pelo Valor Nominal N do título.
Desconto por foraDesconto por foraDesconto por foraDesconto por fora Juros simplesJuros simplesJuros simplesJuros simples
D = N i nD = N i nD = N i nD = N i n j = P i nj = P i nj = P i nj = P i n
N = Valor NominalN = Valor NominalN = Valor NominalN = Valor Nominal P = PrincipalP = PrincipalP = PrincipalP = Principal
i = taxa de descontoi = taxa de descontoi = taxa de descontoi = taxa de desconto i = taxa de jurosi = taxa de jurosi = taxa de jurosi = taxa de juros
n = no. de períodosn = no. de períodosn = no. de períodosn = no. de períodos n = no. de períodosn = no. de períodosn = no. de períodosn = no. de períodos
O valor atual no desconto por fora, é calculado por:

A = N-D = N-N.i.n = N(1-i.n)
Desconto Simples Racional (por dentro): O cálculo deste desconto funciona análogo ao cálculo dos juros
simples, substituindo-se o Capital P na fórmula de juros simples pelo Valor Atual A do título.
O cálculo do desconto racional é feito sobre o Valor Atual do título.
Desconto por dentroDesconto por dentroDesconto por dentroDesconto por dentro Juros simplesJuros simplesJuros simplesJuros simples
D = A i nD = A i nD = A i nD = A i n j = P.i.nj = P.i.nj = P.i.nj = P.i.n
N = Valor AtualN = Valor AtualN = Valor AtualN = Valor Atual P = PrincipalP = PrincipalP = PrincipalP = Principal
i = taxa de descontoi = taxa de descontoi = taxa de descontoi = taxa de desconto i = taxa de jurosi = taxa de jurosi = taxa de jurosi = taxa de juros
O valor atual, no desconto por dentro, é dado por:
A = N / (1 + i n)
Desconto Comercial composto (por fora): Este tipo de desconto não é usado no Brasil e é análogo ao cálculo
dos Juros compostos, substituindo-se o Principal P pelo Valor Nominal N do título.
Desconto composto por foraDesconto composto por foraDesconto composto por foraDesconto composto por fora Juros compostosJuros compostosJuros compostosJuros compostos
A = N(1-i)nA = N(1-i)nA = N(1-i)nA = N(1-i)n S = P(1+i)nS = P(1+i)nS = P(1+i)nS = P(1+i)n
A = Valor AtualA = Valor AtualA = Valor AtualA = Valor Atual P = PrincipalP = PrincipalP = PrincipalP = Principal
i = taxa de desconto negativai = taxa de desconto negativai = taxa de desconto negativai = taxa de desconto negativa i = taxa de jurosi = taxa de jurosi = taxa de jurosi = taxa de juros
Apenas para fins didáticos, iremos obter a fórmula para o cálculo deste desconto. Ela é obtida por aplicações
repetidas do desconto simples para 1 período.
Para n=1, o desconto composto por fora funciona como o desconto simples por fora, logo:
A1 = N(1-i)
onde A1 é o valor atual do título com valor nominal N. Para n=2, devemos reaplicar o mesmo processo,
substituindo agora N por A1, para obter A2, isto é:
A2 = A1(1-i) = N(1-i)2
Por este raciocínio, temos que, para cada número natural n:
An = N(1-i)n
Esta fórmula é similar à formula do montante composto, dada por:
S = P(1+i)n
Desconto Racional composto (por dentro): Este tipo de desconto é muito utilizado no Brasil.
Como D = N - A e como N = A(1 + i)n , então

D = N-N(1+i)-n = N.[1-(1+i)-n]
O melhor estudo que se pode fazer com o desconto racional composto é considerar o Valor Atual A como o
capital inicial de uma aplicação e o Valor Nominal N como o montante desta aplicação, levando em
consideração que as taxas e os tempos funcionam de forma similar nos dois casos.
Exemplo a: Qual é o desconto racional composto de um título cujo valor nominal é R$10.000,00, se o prazo
de vencimento é de n=5 meses e a taxa de desconto é de 3,5% ao mês.
Solução:
D = 10.000,00 [(1,035)5-1]/1,0355 = 1.580,30
Exemplo b: Uma empresa emprestou um valor que deverá ser pago 1 ano após em um único pagamento de
R$ 18.000,00 à taxa de 4,5% ao mês. Cinco meses após ter feito o empréstimo a empresa já tem condições de
resgatar o título. Se a empresa tiver um desconto racional composto calculado a uma taxa equivalente à taxa
de juros cobrada na operação do empréstimo, qual será o valor líquido a ser pago pela empresa?
Dados: Valor nominal: N=18.000,00; taxa mensal: i=4,5%=0,045
Número de períodos para o desconto: n=12-5=7
Fórmula: D = N.[(1+i)n-1]/(1+i)n
Financiamento pelo Sistema Price
No estudo do financiamento de um bem de consumo, percebe-se que a Matemática Financeira é muito mais
útil no nosso cotidiano do que outras "matemáticas". Aqui se vê a força do estudo de sequências geométricas
(PG), fato que não é possível explicitar facilmente a alunos de níveis elementares. No entanto, praticamente
todos os indivíduos estão envolvidos com compras de bens de consumo no seu dia-a-dia e este ponto se
torna fundamental pois transforma o estudo de Progressões Geométricas em algo extremamente útil.
O sistema Price (Richard Price), também chamado Sistema Francês (pois foi a França o primeiro país que
utilizou este sistema do ponto de vista comercial), corresponde a um financiamento onde todos os
pagamentos sao iguais.
A idéia essencial neste contexto é construir um fluxo de caixa e descobrir o Valor Atual ou Valor Presente
de uma série uniforme de pagamentos.
Antes de continuar, iremos mostrar uma situação para identificar o que está escondido sob os cálculos de
um financiamento.
Exemplo: Suponhamos que uma pessoa compre um carro para pagar em 4 prestações mensais consecutivas e
iguais de R$8.000,00, sem entrada e com taxa de 10% ao mês. Qual será o Valor Atual (real) deste carro?
Fluxo de caixa do problema
O que se deve fazer é calcular o valor atual de cada prestação e realizar a soma desses valores para obter o
Valor Atual do bem financiado.

A1 = 8000/(1+0,1)1
A2 = 8000/(1+0,1)2
A3 = 8000/(1+0,1)3
A4 = 8000/(1+0,1)4
Assim o Valor Atual será a soma dos valores atuais parciais
A = 8000.(1,1-1 + 1,1-2 + 1,1-3 + 1,1-4)
que pode ser escrito como:
A = 8000 x 3,169865435 = 25.358,92
que é o valor à vista que custa o carro.
Um fato curioso é o aparecimento da expressão:
K = 1,1-1 + 1,1-2 + 1,1-3 + 1,1-4
que representa a soma dos termos de uma sequência geométrica (PG) com 4 termos.
Na sequência, analisaremos a situação geral quando temos n prestações num modelo semelhante,
considerando agora um financiamento cujo Valor Atual A na data inicial (tempo=0) será pago em n
prestações iguais a R ao final de cada um dos n meses seguidos, a taxas mensais iguais a i.
Fluxo de caixa do problema
O problema é similar ao anterior e pode ser resolvido do ponto de vista matemático, como :
A = R[(1+i)-1+(1+i)-2+...+(1+i)-n]
Evidenciando o termo (1+i)-n, segue que:
A = R[1+(1+i)1+...+(1+i)n-1] / (1 +i)n
e o termo dentro dos colchetes corresponde à soma dos n primeiros termos de uma PG cujo primeiro termo
é igual 1 e cuja razão é igual a (1+i).
A fórmula abaixo é a expressão matemática procurada por tantas pessoas para saber como são realizados os
cálculos de taxas de juros em financiamentos.
Esta não é uma expressão matemática simples! Quando se conhece a taxa i, o número de períodos n e o
valor de cada prestação R é bastante fácil obter o Valor Atual A.
Quando conhecemos o Valor Atual (preço à vista) A, Prestação R e Número de períodos n, não é fácil obter
a taxa de juros porque além de ser matematicamente difícil, o governo, as empresas e financeiras em geral,
embutem muitas outras taxas a títulos diversos que mascaram o valor real da taxa!
Esta fórmula matemática pode ser escrita como:
A = R FVAs(i,n)
onde FVAs é o Fator de Valor Atual para uma série uniforme, definido por:

Esta é a fórmula utilizada nas tabelas financeiras que encontramos no comércio em geral. Através desta
fórmula podemos obter a taxa de um financiamento em prestações com pagamentos iguais.
Para o próximo exemplo, vamos admitir que o dono de uma loja te garantiu o valor certo para a taxa ao
período, o que eu não acredito em geral.
Para se calcular o valor da prestação R de um bem cujo preço à vista é A e será pago em n prestações iguais
sem entrada, à taxa i ao período, sendo que a primeira prestação será paga no final do primeiro período,
divide-se o valor atual A pelo FVAs(i,n), isto é:
R = A / FVAs(i,n)
Exemplo: Determinar a prestação R da compra de uma geladeira que custa à vista A=$1.000,00 e que será
paga em 12 meses, sem entrada, com um taxa de 5% ao mês.
Aritmética
As operações aritméticas tradicionais são a adição, a subtração, a multiplicação e a divisão, embora
operações mais avançadas (tais como as manipulações de porcentagens, raiz quadrada, exponenciação e
funções logarítmicas) também sejam por vezes incluídas neste ramo. A aritmética desenrola-se em
obediência a uma ordem de operações.
A aritmética abrange o estudo de algoritmos manuais para a realização de operações com os números
naturais, inteiros, racionais (na forma de frações) e reais. Tais operações, no entanto, podem ser realizadas
com o uso de ferramentas como calculadoras, computadores ou o ábaco, o que não lhes tira o caráter
aritmético.
O termo aritmética também é usado em referência à teoria dos números. Isto inclui as propriedades dos
inteiros relacionados com a primalidade, a divisibilidade e a solução de equações em inteiros, bem como a
pesquisa moderna que tem surgido deste estudo. É neste contexto que se pode encontrar coisas como o
teorema fundamental da aritmética e funções aritméticas.
Média aritmética
A média aritmética entre dois números reais positivos x e y, é definida como:
a(x,y)a(x,y)a(x,y)a(x,y) ====
x+yx+yx+yx+y
2222

Exemplo: A média aritmética entre x=6 e y=9 é igual a a(6,9)=(6+9)/2=7,5.
Em teoria dos números, uma função aritmética é uma função f(n) de valor real ou complexa definida sobre
o conjunto dos números naturais (i.e. inteiros positivos) que "expressam alguma propriedade aritmética de
n."[1].
Um exemplo de uma função aritmética é o caráter não-principal (mod 4) definido por
onde é o símbolo de Kronecker.
Para enfatizar que representam funções, em vez de seqüências, os valores de uma função aritmética são
normalmente identificados por a(n) ao invés de an.
Existe uma classe maior de funções em teoria dos números que não se encaixam na definição acima, por
exemplo, e.g., as funções de contagem de primos. Este artigo fornece ligações para as funções de ambas as
classes.
Funções multiplicativas e aditivasFunções multiplicativas e aditivasFunções multiplicativas e aditivasFunções multiplicativas e aditivas
Uma função aritmética a é
• completamente aditiva se a(mn) = a(m) + a(n) para todos os números naturais m e n;
• completamente multiplicativa se a(mn) = a(m)a(n) para todos os números naturais m e n;
Dois números inteiros m e n são chamados coprimos se seu máximo divisor comum é 1; i.e., se não há
número primo que divida ambos.
Então uma função aritmética a é
• aditiva se a(mn) = a(m) + a(n) para todos os números naturais coprimos m e n;
• multiplicativa se a(mn) = a(m)a(n) para todos os números naturais coprimos m e n.
Ω(n), ω(n), νp(n) - decomposição de potências de primosΩ(n), ω(n), νp(n) - decomposição de potências de primosΩ(n), ω(n), νp(n) - decomposição de potências de primosΩ(n), ω(n), νp(n) - decomposição de potências de primos
O teorema fundamental da aritmética estabelece que qualquer inteiro positivo n pode ser fatorado
unicamente como um produto de potências de primos: onde p1 < p2 < ... < pk são
primos e aj são inteiros positivos. (1 é dado pelo produto vazio.)
É frequentemente conveniente escrever isto como um produto infinito sobre todos os primos, onde todos
mas um número finito tem um expoente zero. Define-se νp(n) como o expoente da mais alta potência do
primo p que divide n. I.e. se p é um dos pi então νp(n) = ai, caso contrário, é zero. Então
Em termos do acima as funções ω e Ω são definidas por
ω(n) = k,
Ω(n) = a1 + a2 + ... + ak.
Para evitar repetição, sempre que possível, as fórmulas para as funções listadas neste artigo são dadas em
termos de n e as correspondentes pi, ai, ω, e Ω.

Funções multiplicativasFunções multiplicativasFunções multiplicativasFunções multiplicativas
σk(n), τ(n), d(n) - somas divisorasσk(n), τ(n), d(n) - somas divisorasσk(n), τ(n), d(n) - somas divisorasσk(n), τ(n), d(n) - somas divisoras
σk(n) é a soma das kth potências dos divisores positivos de n, incluindo 1 e n, onde k é um número
complexo.
σ1(n), a soma dos dividores (positivos) de n, é normalmente notada por σ(n).
Já que um número positivo levado à potência zero é um, σ0(n) é consequentemente o número de dividores
(positivos) de n; é normalmente notado por d(n) or τ(n) (do alemão Teiler = divisores).
Fazendo k = 0 no segundo produto temos
φ(n) - Função totiente de Eulerφ(n) - Função totiente de Eulerφ(n) - Função totiente de Eulerφ(n) - Função totiente de Euler
φ(n), a função totiente de Euler, é o número de inteiros positivos não maiores que n que são coprimos a n.
μ(n) - Função de Möbiusμ(n) - Função de Möbiusμ(n) - Função de Möbiusμ(n) - Função de Möbius
μ(n), a função de Möbius, é importante por causa da fórmula da inversão de Möbius. Ver convolução de
Dirichlet, abaixo.
Isto implica que μ(1) = 1. (Porque Ω(1) = ω(1) = 0.)
τ(n) - Função tau de Ramanujanτ(n) - Função tau de Ramanujanτ(n) - Função tau de Ramanujanτ(n) - Função tau de Ramanujan
τ(n), a função tau de Ramanujan, é definida por sua identidade da função geradora:
Embora seja difícil dizer exatamente o que "propriedade aritmética de n" "expressa",(τ(n) é (2π)−12 vezes o
coeficiente de Fourier nth na expansão q da forma modular da função discriminant modular)que seja
incluída entre as funções aritméticas, porque é multiplicativa e ocorre em identidades envolvendo certas
funções σk(n) e rk(n) (porque estas são também coeficientes na expansão das formas modulares).
cq(n) - Soma de Ramanujancq(n) - Soma de Ramanujancq(n) - Soma de Ramanujancq(n) - Soma de Ramanujan
cq(n), a soma de Ramanujan, é a soma de nth potências das raízes da unidade qth:

Mesmo que seja definido como uma soma de números complexos (irracionais para a maioria dos valores de
q), é um número inteiro. Para um valor fixo de n multiplicativo em q:
Se q e r são coprimos,

63161537 matematica

Mais conteúdo relacionado

Mais procurados

Semelhante a 63161537 matematica

63161537 matematica