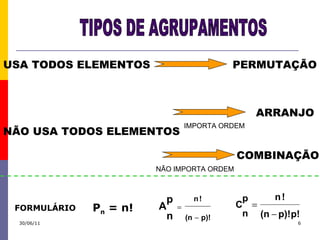
O documento apresenta conceitos de combinatória e probabilidade, incluindo fatorial, permutação, arranjo e combinação. Explica o princípio fundamental da contagem e apresenta exemplos de cálculos de possibilidades e probabilidades para eventos compostos por etapas independentes.

1. ANÁLISE COMBINATÓRIA FATORIAL 5! = 5.4.3.2.1 = 120 4! = 4.3.2.1 = 24 3! = 3.2.1 = 6 2! = 2.1 = 2 1! = 1 0! = 1 CONVENÇÃO Exemplo: Calcular o valor de: a) 4! + 3! b) 7! 24 + 6 30 7.6.5.4.3.2.1 5040 Observe que: 4!+3!  7! c) n! = n.(n  1) . (n  2) . (n  3). .... 2 . 1 = 8! 10. 9. 8! 90 = 30/06/11 Professor: Josivaldo Passos.

2. d) – 49! 49! 50 . 49! 49! (50 – 1) 49! 49 O conjunto solução de: é: (n – 1)! = 210 (n + 1)! = (n + 1).n.(n – 1).(n – 2).(n – 3).... (n + 1)! = (n + 1).n.(n – 1)! (n + 1).n.(n – 1)! (n + 1).n = 210 n 2 + n – 210 = 0 n’ = 14 n’’ = - 15 ( não convém ) Determine a soma dos valores de m que satisfazem a equação (m – 3)! = 1 (m – 3)! = 1! ou (m – 3)! = 0! m – 3 = 1 m = 4 m – 3 = 0 m = 3 Logo a soma dos valores de m é 7 30/06/11

3. PRINCÍPIO FUNDAMENTAL DA CONTAGEM O princípio fundamental da contagem, ou princípio multiplicativo, estabelece um método indireto de contagem de um determinado evento, sem que haja a necessidade de descrever todas as possibilidades. Pode ser enunciado dessa forma: Se um Evento E pode acontecer por n etapas sucessivas e independentes de modo que: E 1 é o número de possibilidades da 1ª Etapa E 2 é o número de possibilidades da 2ª Etapa : : E n é o número de possibilidades da n-ésima Etapa Então E 1 . E 2 . ......... .E k é o número total de possibilidades do evento ocorrer. Quantas placas para identificação de veículos podem ser confeccionadas com 3 letras e 4 algarismos? (Considere 26 letras, supondo que não há nenhuma restrição.) 26 26 26 10 10 10 10 = 175. 760. 000 30/06/11

4. Quantos números de telefones com sete algarismos e prefixo 244 podem ser formados ? Alguns números possíveis 244 3215 244 5138 244 0008 244 2344 244 0000 : : : Usando o princípio fundamental da contagem: 244 10 10 10 10 = 10 000 números fixo 30/06/11

5. Numa olimpíada de Matemática concorrem 100 participantes e serão atribuídos dois prêmios, um para o 1º lugar e outro para o 2º lugar. De quantas maneiras poderão ser distribuídos esses prêmios? 99 100 = 9900 maneiras 30/06/11

6. TIPOS DE AGRUPAMENTOS USA TODOS ELEMENTOS NÃO USA TODOS ELEMENTOS PERMUTAÇÃO ARRANJO COMBINAÇÃO IMPORTA ORDEM NÃO IMPORTA ORDEM P n = n! FORMULÁRIO 30/06/11

7. EXERCÍCIOS: 1. De quantos modos distintos podemos colocar 3 livros juntos em uma estante de biblioteca? Resposta: 6 2. Qual é o número possível de anagramas que se pode montar com as letras da palavra AMOR? Resposta: 24 30/06/11

8. 3. Quantos números com cinco algarismos distintos, podemos construir com os números ímpares 1,3,5,7,9? Resposta: 120 4. Quantos números com cinco algarismos podemos construir com os números ímpares 1,3,5,7,9, desde que estejam sempre juntos os algarismos 1 e 3? Resposta: 48 5. Quantos são os anagramas possíveis com as letras: ABCDEFGHI, começando por AB? Resposta: 5040 30/06/11

9. 6. Há 10 pessoas em um local, sendo 3 com camisas verdes, 3 com camisas amarelas, 2 com camisas azuis e 2 com camisas brancas. De quantos modos podemos perfilar todas essas 10 pessoas de modo que os grupos com as camisas de mesma cor fiquem juntos? Resposta: 3456 7. Quantos grupos de 3 pessoas podem ser montados com 8 pessoas? Resposta: 56 30/06/11

10. 8. Quantos grupos de 2 pessoas podem ser montados com 1000 pessoas? Resposta: 499500 9. Em uma sala existem 20 pessoas, 8 mulheres e 12 homens. Quantas comissões podem ser montadas nesta sala contendo 3 mulheres e 5 homens? Resposta: 44352 30/06/11

11. 10. Para resolver um assunto entre 6 professores e 4 alunos, devemos formar comissões com 3 professores e 2 alunos. Quantas são as possibilidades? Resposta: 120 11. Quantos números distintos com 2 algarismos diferentes, podemos formar com os dígitos: 0,1,2,3,4,5,6,7,8,9. Resposta: 81 30/06/11

12. 12. Usando-se apenas os algarismos 1,3,5,7,9 quantos números com 3 algarismos podem ser montados? Resposta: 60 13. Usando-se as 26 letras do alfabeto: A,B,C,D,...,Z quantos arranjos distintos com 3 letras podem ser montados? Resposta: 15600 30/06/11