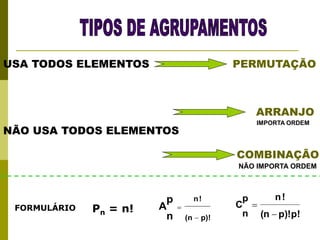
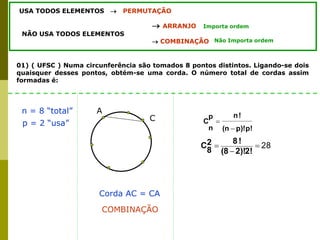
O documento apresenta conceitos fundamentais de combinatória como fatorial, permutação, arranjo e combinação. Explica como calcular o número de possibilidades para diferentes eventos usando as fórmulas apropriadas, como o número de formas de distribuir prêmios em uma competição ou formar placas de identificação de veículos.

1. ANÁLISE COMBINATÓRIA
FATORIAL
5! = 5.4.3.2.1 = 120
4! = 4.3.2.1 = 24
3! = 3.2.1 = 6
2! = 2.1 = 2
1! = 1
0! = 1 CONVENÇÃO
Exemplo: Calcular o valor de:
a) 4! + 3! b) 7!
24 + 6
30
7.6.5.4.3.2.1
5040
Observe que:
4!+3!  7!
c)
!
8
!
10
n! = n.(n  1) . (n  2) . (n  3). .... 2 . 1
=
8!
10.9.8! 90
=

2. d)
!
49
!
49
!
50 
– 49!
49!
50.49!
49!(50 – 1)
49!
49
O conjunto solução de:
210
)!
1
(
)!
1
(



n
n é:
(n – 1)!
= 210
(n + 1)! = (n + 1).n.(n – 1).(n – 2).(n – 3)....
(n + 1)! = (n + 1).n.(n – 1)!
(n + 1).n.(n – 1)!
(n + 1).n = 210
n2 + n – 210 = 0
n’ = 14 n’’ = - 15
(não convém)
Determine a soma dos valores
de m que satisfazem a equação
(m – 3)! = 1
(m – 3)! = 1! ou (m – 3)! = 0!
m – 3 = 1
m = 4
m – 3 = 0
m = 3
Logo a soma dos valores de m é 7
210
)!
1
(
)!
1
(



n
n

3. PRINCÍPIO FUNDAMENTAL DA CONTAGEM
O princípio fundamental da contagem, ou princípio multiplicativo,
estabelece um método indireto de contagem de um determinado evento,
sem que haja a necessidade de descrever todas as possibilidades.
Quantas placas para identificação de veículos podem ser confeccionadas
com 3 letras e 4 algarismos?
(Considere 26 letras, supondo que não há nenhuma restrição.)
26
26 26 10
10 10 10 = 175. 760. 000

4. Quantos números de telefones com sete algarismos e prefixo 244 podem
ser formados ?
Alguns números possíveis
244 3215
244 5138
244 0008
244 2344
244 0000
:
:
:
Usando o princípio fundamental da contagem:
244
10
10 10
10
= 10 000 números
fixo

5. Numa olimpíada de Matemática concorrem 100 participantes e serão
atribuídos dois prêmios, um para o 1º lugar e outro para o 2º lugar. De
quantas maneiras poderão ser distribuídos esses prêmios?
99
100
= 9900 maneiras

6. USA TODOS ELEMENTOS
NÃO USA TODOS ELEMENTOS
PERMUTAÇÃO
ARRANJO
COMBINAÇÃO
IMPORTA ORDEM
NÃO IMPORTA ORDEM
Pn = n!
p)!
(n
!
n
p
n
A


p!
p)!
(n
!
n
p
n
C


FORMULÁRIO

7. 01) ( UFSC ) Numa circunferência são tomados 8 pontos distintos. Ligando-se dois
quaisquer desses pontos, obtém-se uma corda. O número total de cordas assim
formadas é:
n = 8 “total”
p = 2 “usa”
A
C
Corda AC = CA
COMBINAÇÃO
p!
p)!
(n
!
n
p
n
C


28



2)!2!
(8
!
8
2
8
C
USA TODOS ELEMENTOS  PERMUTAÇÃO
 ARRANJO
NÃO USA TODOS ELEMENTOS
 COMBINAÇÃO
Importa ordem
Não Importa ordem

8. EX:1:Quantos números de 5 algarismos distintos formamos
com os algarismos 1,2,3,4,5,6,7,8 e 9?
A(9,5) = 9!/(9-5)! = 9.8.7.6.5.4!/4! = 15 120
Ex:2: Um anagrama é um código formado pela transposição (troca)
de todas as letra de uma palavra, podendo ou não ter significado na
língua de origem. Por ex., BOCA e ABOC são anagramas da palavra
CABO.
Considere , agora, a palavra LIVRO.
a) Quantos anagramas são formados com as letras dessa palavra?
b) Quantos deles começam por L e terminam por O?
c) Quantos contêm as letras RO juntas e nessa ordem?

9. USA TODOS ELEMENTOS  PERMUTAÇÃO ( trocar de lugar)
 ARRANJO
NÃO USA TODOS ELEMENTOS
 COMBINAÇÃO
Importa ordem
Não Importa ordem
Permutações com
elementos repetidos
Se entre os n elementos
de um conjunto, existem
a elementos repetidos, b
elementos repetidos, c
elementos repetidos e
assim sucessivamente ,
o número total de
permutações que
podemos formar é dado
por:
Permutações com elementos repetidos
Determine o número de anagramas
da palavra MATEMÁTICA.(não
considere o acento)
Pn
(a,b,c,...) = n! / a!b!c!...

10. 04) Determine o número de anagramas da palavra CARCARÁ (não considere o
acento)
USA TODOS ELEMENTOS  PERMUTAÇÃO
 ARRANJO
NÃO USA TODOS ELEMENTOS
 COMBINAÇÃO
Importa ordem
Não Importa ordem
210
!
2
!
2
!
3
!
7
3,2,2
7
P 

56
!
3
!
5
!
8
5,3
8
P 


11. 06) Os presentes a determinada reunião, ao final da mesma, cumprimentam-se
mutuamente, com aperto de mão. Os cumprimentos foram em número de 28. O
número de pessoas presentes à reunião é:
USA TODOS ELEMENTOS  PERMUTAÇÃO
 ARRANJO
NÃO USA TODOS ELEMENTOS
 COMBINAÇÃO
Importa ordem
Não Importa ordem
n = x “total”
p = 2 “usa”
COMBINAÇÃO
p!
p)!
(n
!
n
p
n
C


2)!2!
(x
!
x
28


José – Carlos Carlos – José
2)!2.1
(x
2)
-
1)(x
-
x(x
28


56 = x2 - x
x2 – x – 56 = 0
x = 8

12. 07) ( UEL-PR ) Seis gremistas e um certo número de colorados assistem a um Grenal.
Com o empate final, todos os colorados cumprimentam-se entre si uma única vez, e
todos os gremistas cumprimentam-se entre si uma única vez,havendo no total 43
cumprimentos. O número de colorados é:
USA TODOS ELEMENTOS  PERMUTAÇÃO
 ARRANJO
NÃO USA TODOS ELEMENTOS
 COMBINAÇÃO
Importa ordem
Não Importa ordem
43
2
x
C
2
6
C 

43
2)!2!
(x
!
x
2)!2!
(6
!
6




43
2)!2.1
(x
2)
-
1)(x
-
x(x
15 


x2 – x =56
x2 – x – 56 = 0
x = 8

13. USA TODOS ELEMENTOS  PERMUTAÇÃO
 ARRANJO
NÃO USA TODOS ELEMENTOS
 COMBINAÇÃO
Importa ordem
Não Importa ordem
08) ( UFSC ) Assinale a(s) proposição(ões) CORRETA(S).
2
x
A
01. A equação = 12 não possui solução.
12
!
2)
(x
!
2)
1)(x
x(x
12
!
2)
(x
!
x
12
A2
x







x(x – 1) = 12
x2 – x – 12 = 0
x1 = 4 ou x2 = – 3 (não serve).
F
02. Com a palavra CAJU podemos formar
24 anagramas
Pn =
n!
P4 = 4! = 24
V
04. Numa sala estão 5 professores e 6
alunos. O número de grupos que
podemos formar, tendo 2
professores e 3 alunos, é 30.
200
20
.
10
3
6
C
.
2
5
C

F
ou  +
e  x
08. Na final do revezamento 4 x 100 m
livre masculino, no Mundial de Natação,
em Roma 2009, participaram: Estados
Unidos, Rússia, França, Brasil, Itália,
África do Sul, Reino Unido e Austrália. Os
distintos modos pelos quais poderiam ter
sido distribuídas as medalhas de ouro,
prata e bronze são em número de 56.
7
8
=336
ARRANJO  P.F.C
6
F

14. 09) Assinale a(s) proposição(ões) CORRETA(S).
01. Em uma clínica médica trabalham cinco médicos e dez enfermeiros. Com esse
número de profissionais é possível formar 200 equipes distintas, constituídas cada
uma de um médico e quatro enfermeiros.
02. Entre os anagramas da palavra ÁGUA, 6 começam por consoante. (não
considere o acento)
04. A partir de 12 pontos distintos marcados numa circunferência podem ser
feitos 440 triângulos unindo-se três desses pontos.
08. O total de números pares que se obtém permutando os algarismos 1, 2, 2,
5, 5, 5 e 6 é 180.
1050
.210
5
!
4
!.
6
!
10
.
!
!.1
4
!
5
C
.
C 4
10
1
5 

 F
3
!
2
!
3
P2
3 
 F
220
!
3
.
!
9
!
12
C3
12 
 F
Terminados em 2
Terminados em 6
120
!
3
!
6
P3
6 

60
!
.2
!
3
!
6
P3,2
6 

 TOTAL: 180 V