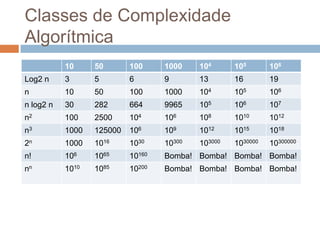
O documento discute a eficiência de algoritmos e a análise da complexidade algorítmica. Aborda como medir o tempo e espaço de execução de algoritmos e como classificar sua complexidade, variando entre classes como constante, logarítmica e exponencial. Também apresenta notações matemáticas como O, Ω, Θ e ω para comparar taxas de crescimento de funções.

1. COMPLEXIDADE DE
PROBLEMAS
Prof.: Marlon Vinicius da Silva
Disciplina: Computação e Algoritmo I

2. Eficiência de algoritmos

Que recursos computacionais são necessários
para executar um algoritmo?
 Tempo
de execução = Complexidade Temporal
 Espaço de memória = Complexidade Espacial

Espaço e tempo dependem da dimensão dos
dados. Podemos portanto representar a
eficiência por funções!

3. Eficiência de algoritmos


Na prática é muito difícil calcular com rigor o
tempo de execução de um algoritmo!
Identificar no algoritmo as operações elementares
e determinar o número de vezes que são
executadas.
O tempo real de execução de cada operação
elementar será uma constante multiplicativa!
 Independentemente do computador!


Dados vários algoritmos para solucionar um
mesmo problema, devemos escolher aquele que
nos permite resolver o problema mais
rapidamente e utilizando o menor espaço possível
para representar os dados do problema!

4. Eficiência de algoritmos



Um algoritmo pode ser mais eficiente que
outro para inputs de “pequena” dimensão e
deixar de o ser para inputs de “grande”
dimensão.
Um algoritmo pode ser mais eficiente que
outro em tempo e não o ser em espaço.
Mais ainda, diferentes amostras com a mesma
dimensão podem ser processadas em tempos
diferentes, podendo-se falar de eficiência
temporal mínima (melhor caso), máxima
(pior caso) e média.

5. Ordem de Complexidade


Normalmente a análise de algoritmos é
simplificada se nos concentrarmos na sua
eficiência assintótica.
Exemplos:
 (n+1)/2
= O(n)
 2n3+2n -7 = O(n3)
 (n2+5)(n-3) = O(n3)
 ln n = O(log2 n)
 25 = O(n0) = O(1)

6. Classes de Complexidade
Algorítmica









O(1) Complexidade Constante
O(log n) Complexidade Logarítmica
O(n) Complexidade Linear
O(n log n) Complexidade Log-Linear
O(n2) Complexidade Quadrática
O(n3) Complexidade Cúbica
O(nk) Complexidade Polinomial
O(an) Complexidade Exponencial
O(n!) Complexidade Factorial

7. Classes de Complexidade
Algorítmica
10
50
100
1000
104
105
106
Log2 n
3
5
6
9
13
16
19
n
10
50
100
1000
104
105
106
n log2 n
30
282
664
9965
105
106
107
n2
100
2500
104
106
108
1010
1012
n3
1000
125000
106
109
1012
1015
1018
2n
1000
1016
1030
10300
103000
1030000
10300000
n!
106
1065
10160
Bomba! Bomba! Bomba! Bomba!
nn
1010
1085
10200
Bomba! Bomba! Bomba! Bomba!

8. Classes de Complexidade
Algorítmica

Com 210 ≈103 , logo, Bomba! ≈ número grande
inimaginável







1 dia 24 X 60 X 60 = 86400 ≈ 9 X 1010 microssegundos
1 ano = 365 X 24 X 60 X 60 § 3 X 107 segundos ≈3 X 1013
microssegundos
1 século ≈ 3 X 109 segundos ≈ 3 X 1015 microssegundos
1 milênio ≈ 3 X 1010 segundos ≈ 3 X 1016 microssegundos
Big Bang ≈ 15 X 109 anos ≈ 45 X 1016 segundos ≈ 45 X
1022 microssegundos
Algoritmos de complexidade constante e logarítmica
são os mais eficientes
Algoritmos de complexidade exponencial geram
tempos de execução incomputáveis

9. Complexidade de um problema

O limite superior é estabelecido pelo melhor
algoritmo, entre os algoritmos conhecidos.
A
descoberta de um novo algoritmo mais eficiente
faz descer o limite superior.

O limite inferior é estabelecido por técnicas de
prova que comprovem que não existem
algoritmos mais eficientes.
 Qualquer
algoritmo, conhecido ou desconhecido,
deverá ser mais complexo do que esse limite.

10. Notações

Θ(theta) – A expressão f(n) = Θ(g(n)) significa que as
funções f(n) e g(n) possuem a mesma ordem de
crescimento, isto é, crescem de forma equiparável.



As funções n2 e 5n2, por exemplo, crescem em ritmo
quadrático.
O(O maiúsculo ou big o) – A expressão f(n) =
O(g(n)) significa que f(n) não cresce mais que g(n),
podendo crescer de forma igual ou inferior.
o (o minúsculo) – e f(n) = O(g(n)), a ordem de
crescimento de f(n) nunca será maior que a de g(n),
podendo ser igual. Entretanto, se f(n) = o(g(n)), a
ordem de crescimento de f(n) nunca será maior nem
igual à de g(n)

11. Notações


Ω(Omega maiúsculo) – A expressão f(n) =
Ω(g(n)) significa que a ordem de crescimento
de f(n) é maior ou igual à ordem de g(n)
ω(ômega minúsculo) - A notação ω denota
um limite assintótico inferior, assim como Ω. A
diferença é que, se f(n) = ω(g(n)),
para qualquer constante c > 0 que multiplique
g(n) existe um n0 > 0 tal que para todo n ≥ no,
f(n) nunca será menor nem igual a g(n).
Assim, diferentemente de Ω, o crescimento da
função f(n) nunca se igualará ao de g(n).

12. Notações

A analogia com números reais tornou o
entendimento das notações mais intuitivo,
com a visualização das regras:
 f(n)
= O(g(n)) ≈ a ≤ b,
 f(n) = Ω(g(n)) ≈ a ≥ b,
 f(n) = Θ(g(n)) ≈ a = b,
 f(n) = o(g(n)) ≈ a < b,
 f(n) = ω(g(n)) ≈ a > b.