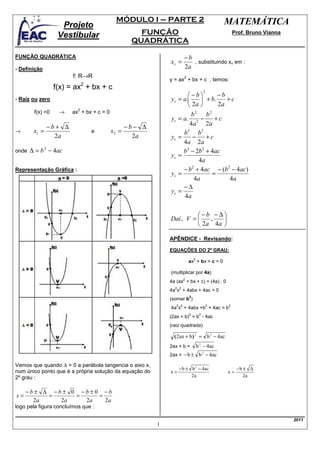
1. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
FUNÇÃO QUADRÁTICA −b
xv = , substituindo xv em :
- Definição 2a
f: R→R 2
y = ax + bx + c , temos:
2
f(x) = ax + bx + c
−b −b
2
- Raíz ou zero yv = a.  + b. +c
 2a  2a
→
2
f(x) =0 ax + bx + c = 0 b2 b2
yv = a. 2 − +c
−b+ ∆ −b− ∆
4a 2a
→ x1 = e x2 = b2 b 2
2a 2a yv = − +c
4a 2a
onde ∆ = b 2 − 4ac b 2 − 2b 2 + 4ac
yv =
4a
Representação Gráfica : − b + 4ac − (b 2 − 4ac)
2
yv = =
4a 4a
−∆
yv =
4a
−b −∆
Daí , V =  , 
 2a 4a 
APÊNDICE - Revisando:
EQUAÇÕES DO 2º GRAU:
2
ax + bx + c = 0
(multiplicar por 4a)
2
4a (ax + bx + c) = (4a) . 0
2 2
4a x + 4abx + 4ac = 0
2
(somar b )
2 2 2 2
4a x + 4abx +b + 4ac = b
2 2
(2ax + b) = b - 4ac
(raiz quadrada)
( 2ax + b ) 2 = b 2 − 4ac
2ax + b = b 2 − 4ac
2ax = − b ± b 2 − 4ac
Vemos que quando ∆ = 0 a parábola tangencia o eixo x,
− b ± b 2 − 4ac −b ± ∆
num único ponto que é a própria solução da equação do x= x=
2º grau : 2a 2a
−b± ∆ −b± 0 −b±0 −b
x= = = =
2a 2a 2a 2a
logo pela figura concluímos que :
2011
1

2. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
Soma das raízes: EXERCÍCIOS DE FIXAÇÃO
S = x1 + x2
2
− b + ∆ − b − ∆ − b − b −2 b − b 01) Dada a função f(x) = -x + 4x + 5 , o gráfico da
S= + = = = mesma está representado abaixo:
2a 2a 2a 2a a
Produto das raízes: V
P = x1 . x2
  
P =  −b + ∆   −b − ∆  = (−b) − ( ∆ ) = b − ∆ =
2 2 2
C
2 2
 2a  2a  4a 4a
b − b + 4ac 4ac c
2 2
A B
= =
4a 2 4aa a
−b c
S= e P= As coordenadas corretas dos pontos do gráfico são:
a a
Resolução de alguams equações do 2º grau incompletas: (A) C=(0,5) ; A=(-1,0) ; B=(5,0) ; V=(3,9)
(B) C=(0,4) ; A=(0,-1) ; B=(0,5) ; V=(2,9)
2 2
a) x - 25 = 0 b) x + x = 0 (C) C=(0,5) ; A=(0,-1) ; B=(0,5) ; V=(9,2)
2
x = 25 x (x + 1) = 0 (D) C=(0,5) ; A=(-1,0) ; B=(4,0) ; V=(3,4)
x =± 25 x = 0 ou x + 1 = 0 (E) C=(0,5) ; A=(-1,0) ; B=(5,0) ; V=(2,9)
x=±5 x = 0 ou x = -1
2
02) (CESGRANRIO) - O vértice da parábola f(x) = x + x
2 2
c)3x - 12 = 0 d) 3x - 6x = 0 é o ponto:
2
3x = 12 3x ( x - 2) = 0 (A) (-1,0) (B) (-1/2,-1/4) (C) (0,0)
2
x = 12 / 3 3x = 0 ou x - 2 = 0
x=± 4 x = 0 ou x = 2 (D) (1/2,3/4) (E) (1,2)
x=±2
2
03)O valor mínimo da função real f(x) = x + x + 1, é:
Resolução das equações do 2º grau completas:
2
a) x - 5x + 6 = 0 1 2 3
(A) -1 (B) 0 (C) (D) (E)
− ( −5) ± ( −5) 2 − 4(1)( 6) 5 ± 25 − 24 2 3 4
x= = =
2(1) 2
5± 1 5±1 6 4 04) Dados os dois gráficos abaixo quais das funções
= == x 1 = = 3 e x 2 = = 2
2 2 2 2 abaixo correspondem aos gráfico de f1 e f2
respectivamente:
Resolução por Soma e Produto
4 f2
2
a) x - 5x + 6 = 0 f1
− b −( −5) c 6
S= = =5 e P= = =6
a 1 a 1
Temos que pensar em dois números que somados resultam 5 -4 4
e multiplicados resultam 6. 2 e 3
2 + 3 = 5 e 2 . 3 = 6 . Portanto x1 = 2 e x2 = 3 0 2 4
Observações
Sinais do Delta nº de soluções -16
∆>0 2
2 2
∆=0 1 (A) f1(x) = -x +16 e f2(x) = -x + 4x
2 2
∆<0 nenhuma (B) f1(x) = x -16 e f2(x) = -x + 4x
2 2
(C) f1(x) = -x + 4 e f2(x) = x + 4x
2 2
(D) f1(x) = x - 4x e f2(x) = -x + 36
2 2
(E) f1(x) = x - 4x + 2 e f2(x) = 2x + 3x + 2
2011
2

3. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
05) (A) (B) (C)
(D) (E)
Considerando o gráfico acima referente ao
trinômio do 2º grau y = ax + bx + c , pode-se afirmar
2
que:
(A) a > 0 ; b > 0 ; c < 0
09) (UFRRJ) O custo de produção de um determinado
(B) a > 0; b < 0; c>0 2
artigo é dado por C(x) = 3x - 15x + 21. Se a venda de x
2
(C) a < 0 ; b < 0; c<0 unidades é dada por V(x) = 2x + x, para que o lucro
L(x) = V(x) - C(x) seja máximo, devem ser vendidas:
(D) a < 0 ; b > 0; c<0
(E) a < 0 ; b > 0; c>0 (A) 20 unidades
(B) 16 unidades
EXERCÍCIOS PROPOSTOS (C) 12 unidades
(D) 8 unidades
06) Um soldado entrincheirado em um terreno horizontal (E) 4 unidades
lança uma granada, que parte do nível do solo e
descreve uma trajetória que obedece à equação 10) (UFRJ) - Oscar arremessa uma bola de basquete
cujo centro segue uma trajetória plana vertical de
1 2 2 40
y=− x + x+ , sendo x e y medidas em 1 8
45 9 9 equação y = − x 2 + x + 2 , na qual os valores x e
metros. A distância entre o ponto de lançamento e o 7 7
ponto atingido pela granada no solo, considerado como y são dados em metros.
o eixo Ox, é:
(A) 30 m
(B) 40 m
(C) 50 m
(D) 60 m
07) (UERJ-2005) Numa operação de salvamento
marítimo, foi lançado um foguete sinalizador que
permaneceu aceso durante toda sua trajetória. Oscar acerta o arremesso, e o centro da bola
Considere que a altura h, em metros, alcançada por passa pelo centro da cesta, que está a 3m de altura.
este foguete, em relação ao nível do mar, é descrita por
2
h = 10 + 5t - t , em que t é o tempo, em segundos, após Determine a distância da cesta ao eixo y.
seu lançamento. A luz emitida pelo foguete é útil apenas
a partir de 14 m acima do nível do mar. O intervalo de 11) Num campo de treinamento, um projétil e um míssil
tempo, em segundos, no qual o foguete emite luz útil é são lançados, no mesmo instante, de bases distantes
igual a: 20 km uma da outra. A trajetória do projétil é uma
2
parábola de equação y = -x + 4x, e a trajetória do
(A) 3 (B) 4 (C) 5 (D) 6 míssil é uma reta de equação y = ax + b. Essa situação
está representada no esquema abaixo, em que os eixos
08) (UFF) - Considerem m , n e p números reais e as x e y são graduados em quilômetros.
funções reais f e g de variável real, definidas por f(x)
2
= mx + nx + p e g(x) = mx + p . A alternativa que
melhor representa os gráficos de f e g é:
2011
3

4. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
15) (UERJ) Numa partida de futebol, no instante em que
os raios solares incidiam perpendicularmente sobre o
gramado, o jogador "Chorão" chutou a bola em direção
ao gol, de 2,30m de altura interna. A sombra da bola
descreveu uma reta que cruzou a linha do gol. A bola
descreveu uma parábola e quando começou a cair da
altura máxima de 9 metros, sua sombra se encontrava a
16 metros da linha do gol. Após o chute de "Chorão",
nenhum jogador conseguiu tocar na bola em
movimento.
Determine a e b, sabendo que o míssil deverá atingir o
projétil quando este alcançar a altura máxima da sua
trajetória (ponto E).
12) (UFF-92 – 2ª fase) O lucro mensal L de certa fábrica
2
é dado por L(x) = -x + 18x -32 , sendo x medido em
milhares de peças,e L, em milhões de reais. Calcule o
A representação gráfica do lance em um plano
número de peças que devem ser produzidas
cartesiano está sugerida na figura a seguir:
mensalmente:
x2
a) Para que a fábrica obtenha o lucro máximo. A equação da parábola era do tipo: y = − + k.
36
O ponto onde a bola tocou pela primeira vez foi:
b) Para que o lucro seja de R$ 40.000.000,00.
13) (UERJ-01-1ªex) – A figura abaixo mostra um (A) na baliza.
anteparo parabólico que é representado pela (B) atrás do gol.
(C) dentro do gol.
3 2
função f ( x) = − x + 2 3x (D) antes da linha do gol.
3
f(x)
16) (PUC) Considere a função f:[-8,3]→R, definida por
2
f(x) = x + 12x + 35 . Então a imagem de f é um intervalo
de comprimento:
α
(A) 75 (B) 78 (C) 81 (D) 83 (E) 90
17) (UERJ-06-2ºex)
Um barco percorre seu trajeto de descida de um rio, a
favor da correnteza, com a velocidade de 2 m/s em
0 relação à água. Na subida, contra a correnteza,
x
retornando ao ponto de partida, sua velocidade é de 8
Uma bolinha de aço é lançada da origem e segue uma m/s, também em relação à água.
trajetória retilínea. Ao incidir no vértice do anteparo é
refletida e a nova trajetória é simétrica à inicial, em Considere que:
relação ao eixo da parábola. O valor do ângulo de
incidência α corresponde a: - o barco navegue sempre em linha reta e na direção da
correnteza;
(A) 30º (B) 45º (C) 60º (D) 75º
- a velocidade da correnteza seja sempre constante;
14) Um dia na praia a temperatura atingiu o seu valor
- a soma dos tempos de descida e de subida do barco
máximo às 14 horas. Supondo que neste dia a
seja igual a 10 min.
temperatura f(t) em graus era uma função do tempo t
2
medido em horas, dada por f(t) = - t + bt – 156 quando
Assim, a maior distância, em metros, que o barco pode
8 < t < 20, pede-se:
percorrer, neste intervalo de tempo, é igual a:
(A) 1.250
a) O valor de b
(B) 1.500
(C) 1.750
b) a temperatura máxima atingida neste dia.
(D) 2.000
2011
4

5. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
18) (UFRJ-92) Considere a função y = f(x) definida por: 21) (AFA-00) O retângulo, com base no eixo das
abcissas, está inscrito numa parábola, conforme figura
 y = 4 x, se 0 ≤ x ≤ 2 abaixo. O valor de x que faz esse retângulo ter
 perímetro máximo é
 y = − x + 6 x, se 2 ≤ x ≤ 6
2
(A) 1 y
a) Esboce o gráfico de y = f(x) no intervalo de [0,6] 8
b) Para que valores de x temos f(x) = 5 ? (B) 0,5
19) (UFRJ-98-PNE) Um fabricante está lançandoa série
de mesas “Super 4”. Os tampos das mesas dessa série (C) 0,25
são retangulares e têm 4 metros de perímetro. A fórmica
usada para revestir o tampo custa R$ 10,00 por metro −2 –x x 2 x
quadrado. Cada metro de ripa usada para revestir as (D) 0,125
cabeceiras custa R$ 25,00 e as ripas para as outras
duas laterais custam R$ 30,00 por metro.
22) (ENEM 2010)
R$ 10,00/m2 Nos processos industriais, como na indústria de
cerâmica, é necessário o uso de fornos capazes de
produzir elevadas temperaturas e, em muitas situações,
o tempo de elevação dessa temperatura deve ser
controlado, para garantir a qualidade do produto final e
a economia do processo.
R$ 25,00/m Em uma indústria de cerâmica, o forno é programado
R$ 30,00/m para elevar a temperatura ao longo do tempo de acordo
a) Determine o gasto do fabricante para revestir uma com a função:
mesa dessa série com cabeceira de medida x.
b) Determine as dimensões da mesa da série “Super
4” para a qual o gasto com o revestimento é o maior
possível.
em que T é o valor da temperatura atingida pelo forno,
20) (UFRJ-2001-PNE) Um grupo de 40 moradores de em graus Celsius, e t é o tempo, em minutos, decorrido
uma cidade decidiu decorar uma árvore de Natal desde o instante em que o forno é ligado.
gigante. Ficou combinado que cada um terá um número Uma peça deve ser colocada nesse forno quando a
n de 1 a 40 e que os enfeites serão colocados na árvore temperatura for 48 ºC e retirada quando a temperatura
durante os 40 dias que precedem o Natal da seguinte for 200 ºC.
forma: o morador número 1 colocará 1 enfeite por dia a
partir do 1º dia; o morador número 2 colocará 2 enfeites O tempo de permanência dessa peça no forno é, em
por dia a partir do 2º dia e assim sucessivamente (o minutos, igual a:
morador número n colocará n enfeites por dia a partir do
n-ésimo dia). (A) 100 (B) 108 (C) 128
(D) 130 (E) 150
a) Quantos enfeites terá colocado ao final dos 40
dias o morador número 13? 23) (UFF-2002-2ªf) Um muro, com 6 metros de
comprimento, será aproveitado como parte de um dos
b) A Sra. X terá colocado, ao final dos 40 dias, um lados do cercado retangular que certo criador precisa
total de m enfeites. Sabendo que nenhum morador construir. Para completar o contorno desse cercado o
colocará mais enfeites do que a Sra. X, determine m. criador usará 34 metros de cerca.
Determine as dimensões do cercado retangular de
maior área possível que o criador poderá construir.
2011
5

6. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
24) (UFF-99-2ª f)- A parábola abaixo representa o lucro 26) (UFF-2010-1ªF) Em Mecânica Clássica, a norma G
mensal L (em reais) obtido em função do número de do campo gravitacional gerado por um corpo de massa
peças vendidas de um certo produto. m em um ponto a uma distância d > 0 do corpo é
diretamente proporcional a m e inversamente
proporcional ao quadrado de d.
Seja G = f (d) a função que descreve a norma G do
campo gravitacional, gerado por um corpo de massa
constante m em um ponto a uma distância d > 0 desse
corpo.
É correto afirmar que f (2d) é igual a:
f (d ) f (d )
(A) (B) (C) 4 f (d )
4 2
(D) 2 f (d ) (E) f (d )
27) (UERJ-2010-2ª fase) Um terreno retangular tem 800
m de perímetro e será dividido pelos segmentos PA e
CQ em três partes, como mostra a figura.
Determine:
a) o número de peças que torna o lucro nulo;
b) o(s) valor(es) de x que torna(m) o lucro negativo;
25) (ENEM 09 prova anulada) A empresa WQTU
Cosmético vende um determinado produto x, cujo custo
2
de fabricação de cada unidade é dado pó 3x + 232, e Admita que os segmentos de reta PA e CQ estão
o seu valor de venda é expresso pela função 180x – contidos nas bissetrizes de dois ângulos retos do
116. A empresa vendeu 10 unidades do produto x, terreno e que a área do paralelogramo PAQC tem
contudo a mesma deseja saber quantas unidades medida S.
2
precisa vender para obter um lucro máximo. Determine o maior valor, em m , que S pode assumir.
A quantidade máxima de unidades a serem vendidas
pela empresa WQTU para obtenção do maior lucro é: 28) (UERJ-2007-2ªF)
A foto abaixo mostra um túnel cuja entrada forma
(A) 10 (B) 30 (C) 58 (D) 116 (E) 232 um arco parabólico com base AB=8m e
altura central OC=5,6m.
Questão Melhorada: A empresa WQTU Cosmético
vende um determinado produto P. O custo de fabricação
2
de x unidades de P é dado por 3x + 232, e o valor de
venda de x unidades é dado por 180x – 116. A empresa
vendeu 10 unidades do produto P e deseja saber
quantas unidades precisa vender para obter um lucro
máximo. A quantidade de unidades a serem vendidas
pela empresa WQTU para obtenção desse lucro
máximo é:
(A) 10 (B) 30 (C) 58 (D) 116 (E) 232
Observe, na foto, um sistema de coordenadas
cartesianas ortogonais, cujo eixo horizontal Ox é
2011
6

7. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
tangente ao solo e o vertical Oy representa o eixo 31) (UFF-2010-2ªF-IJ) A figura abaixo representa um
de simetria da parábola. quadrado MNPQ inscrito no quadrado ABCD cuja área
2
Ao entrar no túnel, um caminhão com altura AP mede 16 cm .
igual a 2,45 m, como ilustrado a seguir, toca sua
extremidade P em um determinado ponto do arco
parabólico.
Determine:
a) as medidas de AM e MB para que a área do
2
quadrado MNPQ seja igual a 9 cm ;
b) as medidas de AM e MB para que a área do
Calcule a distância do ponto P ao eixo vertical Oy. quadrado MNPQ seja a menor possível.
Justifique suas respostas.
29) (UERJ-2009-ESP)
Observe a parábola de vértice V, gráfico da função
2
quadrática definida por y = ax + bx + c, que corta o eixo 32) (AFA-03)Observe o gráfico da função f abaixo.
das abscissas nos pontos A e B. y
1 45°
0 x
Sabendo que f é definida por
ax 2 + bx + c , se x < 1

f(x) =  analise as alternativas e
px + k, se x ≥ 1

marque a opção correta.
(A) ac < 0 (C) p = –1
(B) pk ≥ 0 (D) ab > 0
2 33) (UNICAMP - 2002) Uma transportadora entrega,
Calcule o valor numérico de ∆ = b - 4ac, sabendo que com caminhões, 60 toneladas de açúcar por dia. Devido
o triângulo ABV é equilátero. a problemas operacionais, em um certo dia cada
caminhão foi carregado com 500kg a menos que o
usual, tendo sido necessário, naquele dia, alugar mais 4
30) (UFRJ-2010-PNE) Determine a equação da caminhões.
parábola que passa pelo ponto P1 = (0,a) e é tangente
ao eixo x no ponto P2 = (a,0), sabendo que a distância a) Quantos caminhões foram necessários naquele dia?
de P1 a P2 é igual a 4.
b) Quantos quilos transportou cada caminhão naquele
dia?
2011
7

8. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
DESAFIOS GABARITOS
34) (UNICAMP - 2002) Uma piscina, cuja capacidade é 01) E 02) B 03) E 04) B
3
de 120m , leva 20 horas para ser esvaziada. O volume
de água na piscina, t horas após o início do processo de 05) E 06) A 07) A 08) E
2
esvaziamento, é dado pela função V(t) = a(b – t) para 0
≤ t ≤ 20 e V(t) = 0 para t ≥ 20. 09) D 10) 7m 11) a = -2/9 e b = 40/9
a) Calcule as constantes a e b. 12) a) 9.000 b) 6.000 ou 12.000 13) A
b) Faça o gráfico da função V(t) para t ∈ [0,30]. 14) a) 28 b) 40º 15) C 16) C
17) B 18) b) x = 5/4 e x = 5
2
35) (AMAN-2005) 19) a) G(x) = 120 + 10x -10x b) ½ m
Um foguete de reconhecimento foi lançado de um ponto
20) a) P13 = 364 b) m = 420
da superfície da Terra e, devido a defeitos estruturais,
precisa ser destruído. Sua trajetória plana segue o 21) B 22) D
23) Quadrado de lado 10 m
gráfico y = − x 2 + 40x − 300.
1
24) a) a =−
Com qual inclinação deve ser lançado um míssil do 50
mesmo local, em trajetória retilínea, para destruir o b) Devem ser vendidas 150 ou 450 peças.
2
foguete no ponto mais distante da Terra? (Obs.: 25) B 26) A 27) 20 000 m
considere o eixo das abscissas a superfície terrestre) 28) x = 3m 29) ∆ = 12
(A) arctg 10 (B) arctg 5 2 2
30) y= x − 2x + 2 2 e
(C) arctg 20 (D) arctg 1 4
2 2
(E) arctg 3 y=− x + 2x − 2 2
4
2 2
31) A) AM = 2 − cm e MB = 2 + cm
2 2
(ou vice-versa)
B) AM = MB = 2 cm
32) D 33) a) 24 caminhões b) 2 500kg
3
34) a) a = e b = 20. b) está no final da lista
10
35) A
2011
8

9. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
Resolução de Algumas questões 50 000 a = – 1000
Questão 23)
1
a=−
50
L(x) = –
Desejamos encontrar
– 12x + 1000 + 350 = 0
x de modo que
Logo,
2
x – 600x + 67500 = 0 ⇔
O perímetro do cercado é dado por :
6 + x + y + x + 6 + y. Assim,
Como o muro de 6m será aproveitado, tem-se que x = 150 peças ou x = 450 peças
34 = x + y + x + 6 + y, ou seja y = 14 – x
Devem ser vendidas 150 ou 450 peças.
A área do cercado é dada por
Questão 27)
2
A = (x + 6) y = (x + 6) (14 – x) = -x + 8x + 84,
PC = AQ = y
0 ≤ x <14 que pode ser representada
graficamente por um arco de parábola, com AD = DP = x
concavidade voltada para baixo e vértice no ponto de
−8
abscissa: xv = = 4 , que fornece o maior valor 2 y + 4 x = 800 ⇒ y + 2 x = 400 ⇒ y = 400 − 2 x
2 ⋅ (−1)
para a área. Portanto, o valor de y no cercado é
y = 14 – x = 14 – 4 = 10. A = y ⋅ x = (400 − 2 x) ⋅ x = −2 x 2 + 400
Logo, o cercado de maior área será o quadrado de lado
igual a 10m. Logo :
− ∆ − (400 2 − 4 ⋅ (−2) ⋅ 0) − (160000 − 0)
AMÁX = = =
Questão 24) 4a 4 ⋅ (−2) −8
a) Se L = 0 , x = 100 é uma das raízes. Como o máximo
de L ocorre para x = 300 a outra raiz é x = 500. O lucro
é nulo para 100 peças ou para 500 peças AMÁX = 20 000 m 2
b) O lucro é negativo para 0 ≤ x < 100 e 500 < x ≤ 600
Questão 28)
(pela simetria da parábola).
c) Equação da parábola: y = ax2 + 5,6
16a + 5,6 = 0 ⇒ a = −0,35
L(x) = a (x – 100) (x – 500) = y = −0,35x2 + 5,6 = 2,45
x = 3m
2
L(x) = a (x – 600 x + 50000)
Como L(0) = – 1000
2011
9

10. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
Questão 29) Questão 30)
Os pontos A = (x1,0) e B =(x2,0) estão situados no eixo
das abscissas logo raízes x1 e x2 são as raízes da
função. Logo:
−b+ ∆ −b− ∆ 
l = AB = x 2 − x1 = 
 2a − =
 2a 

−b+ ∆ +b+ ∆  2 ∆ ∆
l= 
=
 =
 2a  2a a
Observe também que:
yV = h∆VAB
l 3
yV =
2
a 2=4
−∆ ∆ 3 >>
= ⋅ a=2 2
4a a 2
−∆ 3∆
=
4a 2a
4a 3∆ = −2a∆
(4a 3∆ )
2
= (− 2a∆ )
2
16a 2 ⋅ 3∆ = 4a 2 ⋅ ∆2 ( ÷4 a 2 ∆ )
16a 2 ⋅ 3∆ 4a 2 ⋅ ∆2
= 2
y = Ax + Bx + C >>> c = 2 2
4a 2 ∆ 4a 2 ∆
e
4⋅3 = ∆ xv = 2 2
∆ = 12 −B
=2 2
2A
B = −4 2 A
Como 2 2 é raiz:
2
y = Ax + Bx + C
0 = A(2 2 )2 + B . 2 2 + 2 2
0 = 8A + 2 2 B + 2 2 (substituindo)
0 = 8A + 2 2 .( − 4 2 A ) + 2 2
2011
10

11. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
0 = 8A −16A + 2 2 2 2
Portanto AM = 2 − cm e MB = 2 + cm
0 = −8A + 2 2 2 2
8A = 2 2 (ou vice-versa)
2 b) A área A(x) do quadrado MNPQ em função da
A= medida x do segmento AM é dada por
4
Substituindo: B = −4 2 A
2 A( x) = x 2 + (4 − x) 2 = 2 x 2 − 8 x + 16
B = −4 2 ⋅ >>> B = −2
4
Com 0 ≤ x ≤ 4
Portanto uma das funções é:
O valor mínimo de A é atingido na abscissa do
vértice da parábola que é gráfico de A. Logo,
2 2 AM = MB = 2 cm
y= x − 2x + 2 2
4
Questão 33)
A outra basta repetir o processo com a < 0. Seja x o número de caminhões utilizados em um dia
normal e y a quantidade em kg carregada em cada um.
 y ⋅ x = 60.000 (1)

( y − 500) ⋅ ( x + 4 ) = 60.000 (2)
Das relações (1) e (2), temos:
yx + 4y - 500x - 2.000 = yx ∴ y = 500 + 125x (3)
Substituindo-se (3) em (1), vem:
(500 + 125x) x = 60.000 ∴ 125x + 500x - 60.000 = 0
2
x = 20
∴ x + 4x – 480
2
ou
x = −24(não convém)
Substituindo-se x = 20 na relação (3):
y = 500 + 125(20) ∴ y = 3.000
2 2 Assim, naquele dia, temos:
Daí teremos: y=− x + 2x − 2 2 A- x + 4 = 24
4 Resposta: 24 caminhões.
B- y – 500 = 2.500
Questão 31) Resposta: 2.500kg.
a) Os triângulos retângulos AMQ e BNM possuem
ângulos correspondentes congruentes e DESAFIOS
hipotenusas de mesma medida. Portanto, eles são
congruentes e, assim, AM = BN. Como cada lado do Questão 34)
quadrado ABCD tem medida 4 cm, escrevendo-se x =
AM, tem-se AQ = BM = AB − AM = 4 − x. A- Do enunciado, devemos ter:
Aplicando-se o Teorema de Pitágoras no triângulo 2
V(0) = 120, ou seja: a . b = 120 (1)
retângulo AMQ, tem-se 2
V(20) = 0, ou seja: a . (b - 20) = 0 (2)
2 2
Da relação (1), tem-se que a ≠ 0 e b ≠ 0.
x + (4 – x) = 9 Assim, da relação (2), podemos escrever:
(b - 20) = 0 ∴ b = 20
2
2 2 3
Logo x = 2− ou x = 2+ Substituindo o valor de b em (1), temos: a =
10
.
2 2
3
Resposta: a = e b = 20.
10
2011
11

12. MÓDULO I – PARTE 2 MATEMÁTICA
Projeto
Vestibular FUNÇÃO Prof. Bruno Vianna
QUADRÁTICA
3
⋅ (20 - t) para 0 ≤ t ≤
2
B- Do item (a), resulta V(t) =
10
20, e V(t) = 0, para t ≥ 20.
Logo, o gráfico de V(t) para t ∈ [0, 30] é
Onde Ɵ é a inclinação, observe o triângulo:
Questão 35)
O gráfico da Função com seus pontos está
representado abaixo:
100
tg θ =
10
tg θ = 10
θ = arctg 10
O míssil deverá ter a seguinte tragetória:
2011
12