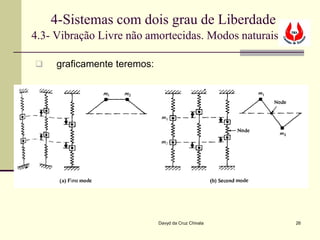
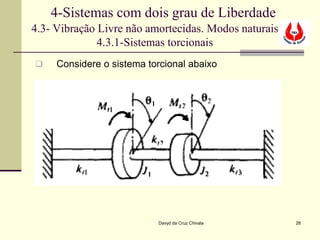
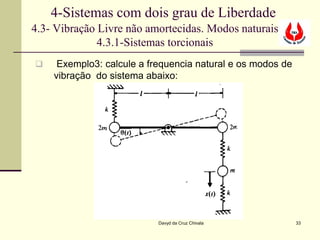
O documento discute sistemas com dois graus de liberdade. Apresenta as equações de movimento para tais sistemas e mostra que eles podem ser representados por matrizes de massa, amortecimento e rigidez. Explica que tais sistemas possuem dois modos naturais de vibração e fornece os métodos para calcular as frequências naturais e os modos de vibração.




![4-Sistemas com dois grau de Liberdade
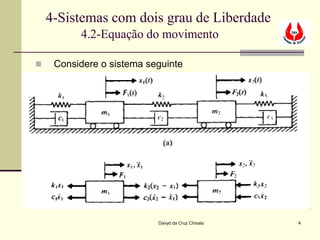
4.2-Equação do movimento
A equação dois na pode ser escrita na forma matricial
fazendo
m1 0 c1 + c2 − c2
0 m = [M ] − c = [C ]
c2 + c3
2 2
k1 + k 2 − k2 (3)
−k = [K ]
k 2 + k3
2
As matrizes apresentadas acima são as matrizes de
massa, amortecimento e de rigidez.
Davyd da Cruz Chivala 6](https://image.slidesharecdn.com/5-sistemascomdoisgraudeliberdade-111222061454-phpapp02/85/5-sistemas-com-dois-grau-de-liberdade-6-320.jpg)
![4-Sistemas com dois grau de Liberdade
4.2-Equação do movimento
x1 (t ) f1 (t )
= {x(t )} = { f (t )} (3)
x2 (t ) f 2 (t )
{ ( )} { ( )}
Os vectores x t ; f t são os vectores de
deslocamento e de força. Assim a equação (2) escreve-
se:
[ ]{ ( )} [ ]{ ( )} [ ]{ ( )} { ( )}
M t + C x t + K x t = f t
x (4)
Davyd da Cruz Chivala 7](https://image.slidesharecdn.com/5-sistemascomdoisgraudeliberdade-111222061454-phpapp02/85/5-sistemas-com-dois-grau-de-liberdade-7-320.jpg)
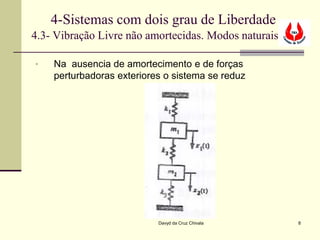


![4-Sistemas com dois grau de Liberdade
4.3- Vibração Livre não amortecidas. Modos naturais
Subistituindo (7) em (6) temos:
[{− m ω + (k + k )}X − k X ]cos(ωt + φ ) = 0
1
2
1 2 1 2 2
[− k X + {− m ω + (k + k )}X ]cos(ωt + φ ) = 0
2 2 2
2
2 3 2
(8)
Uma vez em que os termos de cossenos não podem ser
iguais a zero, então teremos:
{− m ω + (k + k )}X − k X = 0
1
2
1 2 1 2 2
− k X + {− m ω + (k + k )}X = 0
2 (9)
2 2 2 2 3 2
Davyd da Cruz Chivala 11](https://image.slidesharecdn.com/5-sistemascomdoisgraudeliberdade-111222061454-phpapp02/85/5-sistemas-com-dois-grau-de-liberdade-11-320.jpg)








![4-Sistemas com dois grau de Liberdade
4.3- Vibração Livre não amortecidas. Modos naturais
Resorvendo (13) obtemos:
(1)
[{ (1)
} {
X 1 = X 1 cos φ1 + X 1 sin φ1
2 (1)
}]2 12
=
{r2 x1 (0) − x2 (0)}
12
1
2
= {r2 x1 (0 ) − x2 (0 )} +
2
(r2 − r1 ) ω1 2
(2 )
[{ (2 )
} {
X 1 = X 1 cos φ2 + X 1 sin φ2
2 (2 )
}]2 12
=
{r1 x1 (0) − x2 (0)}
12
1
2
= {− r1 x1 (0 ) + x2 (0 )} +
2
(r2 − r1 ) ω2 2
Davyd da Cruz Chivala 20](https://image.slidesharecdn.com/5-sistemascomdoisgraudeliberdade-111222061454-phpapp02/85/5-sistemas-com-dois-grau-de-liberdade-20-320.jpg)
![4-Sistemas com dois grau de Liberdade
4.3- Vibração Livre não amortecidas. Modos naturais
X 1(1) sin φ1 −1 − r2 x1 (0 ) + x2 (0 )
φ1 = tan (1)
−1
= tan
X 1 cos φ1 ω1 [r2 x1 (0 ) + x2 (0 )]
X 1(2 ) sin φ2 −1 r1 x1 (0 ) + x2 (0 )
φ2 = tan (2 )
−1
= tan
X 1 cos φ2 ω2 [− r1 x1 (0 ) + x2 (0 )]
Davyd da Cruz Chivala 21](https://image.slidesharecdn.com/5-sistemascomdoisgraudeliberdade-111222061454-phpapp02/85/5-sistemas-com-dois-grau-de-liberdade-21-320.jpg)
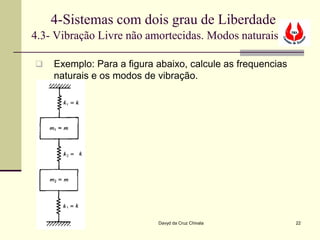

![4-Sistemas com dois grau de Liberdade
4.3- Vibração Livre não amortecidas. Modos naturais
As frequencias serão dadas por:
[ ]
12
4mk − 16k m − 12k m
2 2 2 2 12
k
ω1 = =
2m 2
m
[ ]
12
4mk + 16k 2 m 2 − 12k 2 m
2 12
3k
ω2 = =
2m 2
m
Os racios r1 e r2 serão:
(1)
X2 − mω12 + 2k k
r1 = (1) = = =1
X1 k − mω1 + 2k
2
X 22 ) − mω2 + 2k
( 2
k
r2 = (2 ) = = = −1
X1 k − mω2 + 2k
2 Davyd da Cruz Chivala 24](https://image.slidesharecdn.com/5-sistemascomdoisgraudeliberdade-111222061454-phpapp02/85/5-sistemas-com-dois-grau-de-liberdade-24-320.jpg)