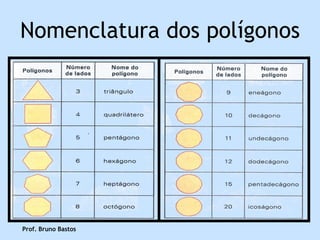
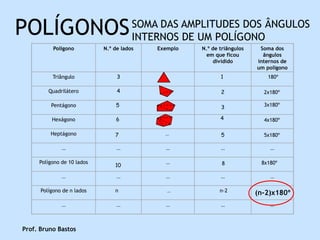
O documento discute polígonos, definindo-os como superfícies planas limitadas por linhas poligonais fechadas. Ele classifica polígonos como convexos ou côncavos dependendo de seus ângulos, e discute a relação entre o número de lados de um polígono e a soma dos ângulos internos e externos.

1. POLÍGONOS

2. POLÍGONOS
Polígono:
superfície plana limitada por uma linha poligonal fechada
Prof. Bruno Bastos

3. POLÍGONOS
Polígono:
superfície plana limitada por uma linha poligonal fechada
Exemplos:
Prof. Bruno Bastos

4. POLÍGONOS
CLASSIFICAÇÃO QUANTO AOS ÂNGULOS:
Prof. Bruno Bastos

5. POLÍGONOS
CLASSIFICAÇÃO QUANTO AOS ÂNGULOS:
Polígono convexo Todos os seus ângulos são
convexos, menores que 1800
(unindo quaisquer dos seus pontos, o segmento de
recta obtido está sempre contido no polígono)
Prof. Bruno Bastos

6. POLÍGONOS
CLASSIFICAÇÃO QUANTO AOS ÂNGULOS:
Polígono convexo Todos os seus ângulos são
convexos, menores que 1800
(unindo quaisquer dos seus pontos, o segmento de
recta obtido está sempre contido no polígono)
Polígono côncavo Tem pelo menos um ângulo
côncavo, maior que 1800
(pelo menos dois dos seus pontos que unidos, formam um
Ângulo segmento de recta que não está contido no polígono)
côncavo
Prof. Bruno Bastos

7. POLÍGONOS
CLASSIFICAÇÃO QUANTO AOS ÂNGULOS:
Polígono convexo Todos os seus ângulos são convexos,
menores que 1800
(unindo quaisquer dos seus pontos, o segmento de
recta obtido está sempre contido no polígono)
Polígono côncavo Tem pelo menos um ângulo
côncavo, maior que 1800
(pelo menos dois dos seus pontos que unidos, formam um
Ângulo segmento de recta que não está contido no polígono)
côncavo
A partir de agora, quando falarmos em polígono estamos a referirmo-nos a polígonos convexos
Prof. Bruno Bastos

8. POLÍGONOS
Prof. Bruno Bastos

9. POLÍGONOS
Prof. Bruno Bastos

10. POLÍGONOS
Ângulo interno:
Ângulo formado pelas semi-rectas
com origem comum num vértice do
polígono e que contém dois lados
consecutivos do polígono.
(os ângulos assinalados a verde são os ângulos
internos)
Prof. Bruno Bastos

11. POLÍGONOS
Ângulo interno:
Ângulo formado pelas semi-rectas
com origem comum num vértice do
polígono e que contém dois lados
consecutivos do polígono.
(os ângulos assinalados a verde são os ângulos
internos)
Ângulo externo:
Ângulo formado por um lado com o prolongamento de um
lado consecutivo
(os ângulos assinalados a amarelo são os ângulos externos)
Prof. Bruno Bastos

12. Nomenclatura dos polígonos
Prof. Bruno Bastos

13. POLÍGONOS SOMA DAS AMPLITUDES DOS ÂNGULOS
INTERNOS DE UM POLÍGONO
Polígono N.º de lados Exemplo N.º de triângulos Soma dos
em que ficou ângulos
dividido internos de
um polígono
Triângulo 3 1 180º
Quadrilátero 4 2 2x180º
Pentágono 5 3 3x180º
Hexágono 6 4 4x180º
Heptágono 7 … 5 5x180º
... ... ... ... ...
Polígono de 10 lados ... 8 8x180º
10
... ... ... ... ...
Polígono de n lados n … n-2 (n-2)x180º
... ... ... ... ...
Prof. Bruno Bastos

14. POLÍGONOS
Prof. Bruno Bastos

15. POLÍGONOS
Pelos valores da tabela pode-se concluir que existe
uma relação entre a soma das amplitudes dos ângulos
internos de um polígono e o número de lados desse
mesmo polígono.
Prof. Bruno Bastos

16. POLÍGONOS
Pelos valores da tabela pode-se concluir que existe
uma relação entre a soma das amplitudes dos ângulos
internos de um polígono e o número de lados desse
mesmo polígono.
A soma Si das amplitudes dos ângulos internos de um
polígono (convexo) com n lados é dada pela
expressão:
Si=(n-2) x 180º
Prof. Bruno Bastos

17. POLÍGONOS SOMA DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS DE UM
POLÍGONO
Prof. Bruno Bastos

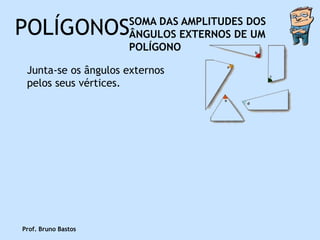
18. POLÍGONOS SOMA DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS DE UM
POLÍGONO
Numa folha de papel, desenha-se o
polígono e os seus ângulos externos. O
polígono [ABCDE] e os seus ângulos
externos a, b, c, d, e
Prof. Bruno Bastos

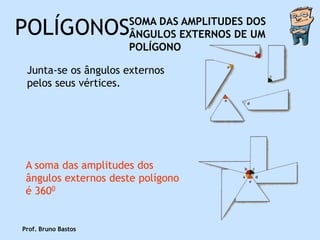
19. POLÍGONOS SOMA DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS DE UM
POLÍGONO
Numa folha de papel, desenha-se o
polígono e os seus ângulos externos. O
polígono [ABCDE] e os seus ângulos
externos a, b, c, d, e
Com uma tesoura, recorta-se cada um
dos ângulos externos, como sugere a
figura.
Prof. Bruno Bastos

20. POLÍGONOS SOMA DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS DE UM
POLÍGONO
Prof. Bruno Bastos

21. POLÍGONOS SOMA DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS DE UM
POLÍGONO
Junta-se os ângulos externos
pelos seus vértices.
Prof. Bruno Bastos

22. POLÍGONOS SOMA DAS AMPLITUDES DOS
ÂNGULOS EXTERNOS DE UM
POLÍGONO
Junta-se os ângulos externos
pelos seus vértices.
A soma das amplitudes dos
ângulos externos deste polígono
é 3600
Prof. Bruno Bastos

23. POLÍGONOS
Utilizando o esquema dos slides anteriores pode-se
concluir que seja qual for o polígono a soma das
amplitudes dos ângulos externos desse polígono é
sempre 3600.
Prof. Bruno Bastos

24. POLÍGONOS
Utilizando o esquema dos slides anteriores pode-se
concluir que seja qual for o polígono a soma das
amplitudes dos ângulos externos desse polígono é
sempre 3600.
A soma Se das amplitudes dos ângulos externos de
um polígono (convexo) é sempre igual a 3600.
Se=3600
Prof. Bruno Bastos

25. FIM
Prof. Bruno Bastos