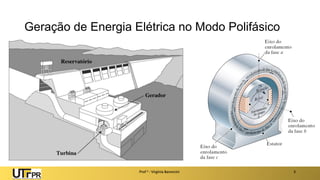
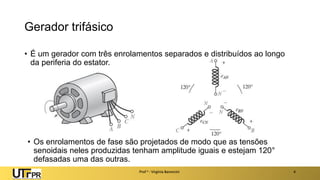
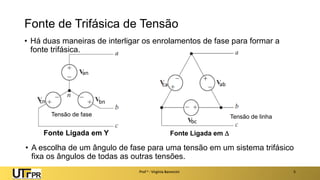
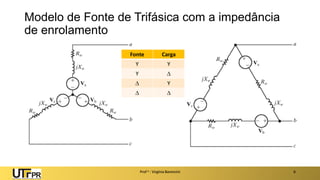
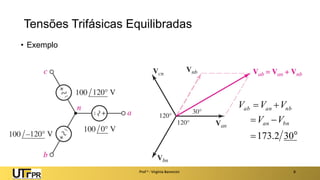
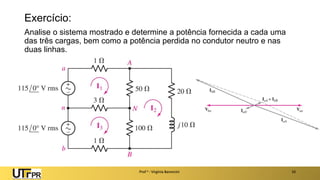
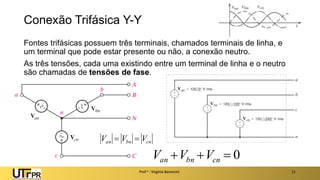
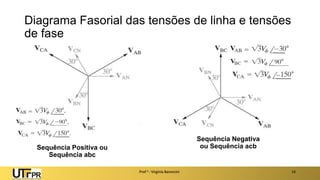
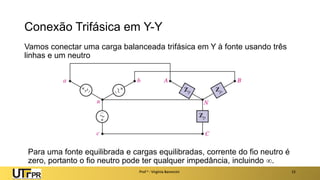
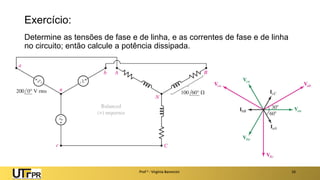
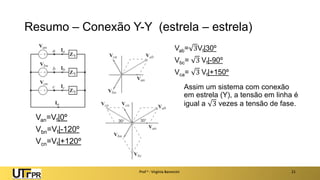
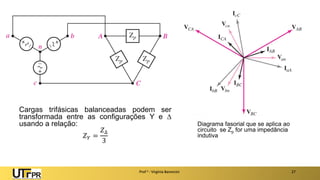
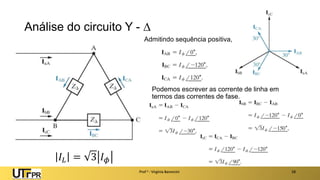
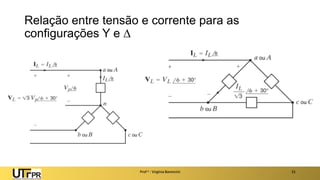
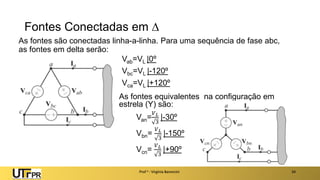
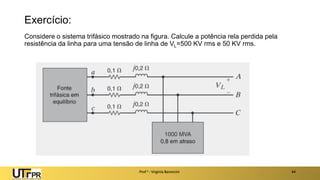
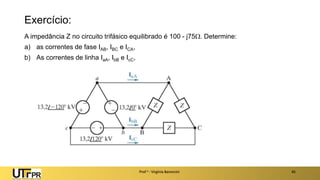
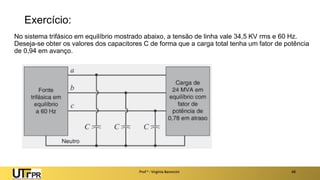
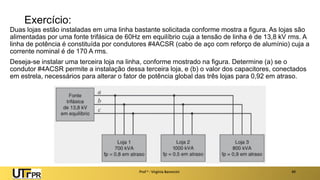
O documento descreve sistemas elétricos polifásicos, explicando que é mais vantajoso transmitir energia no modo polifásico do que monofásico. Sistemas trifásicos permitem o uso de condutores e equipamentos menores para a mesma potência transmitida. Motores trifásicos também têm melhores características de partida e operação em relação aos monofásicos.