O documento apresenta os conceitos básicos de circuitos trifásicos, incluindo:
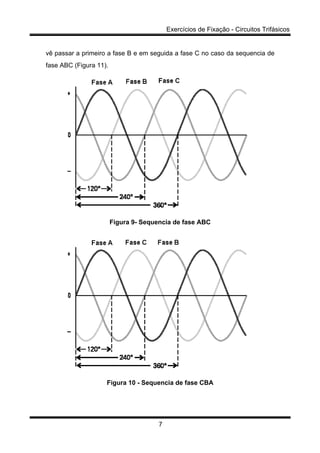
(1) Tensões trifásicas equilibradas são senoidais e defasadas por 120°;
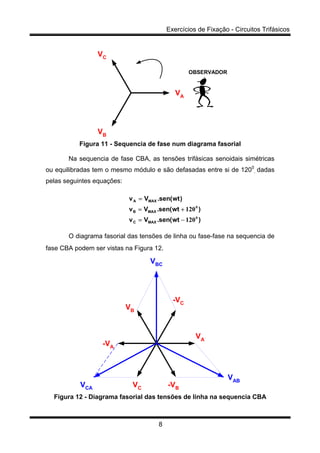
(2) Existem duas sequências de fase possíveis (ABC e CBA);
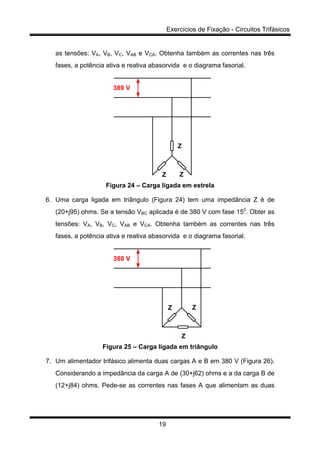
(3) Cargas podem ser ligadas em estrela ou triângulo e afetam as tensões e correntes aplicadas.