1. O documento apresenta os conceitos fundamentais de fasores, impedância complexa, admitância complexa e potência complexa para análise de circuitos elétricos. 2. Inclui detalhes sobre tensões, correntes e diagramas fasoriais em sistemas trifásicos equilibrados nas ligações estrela e delta. 3. Apresenta os conceitos de valores em por unidade e a transformação entre os equivalentes Y-Δ de circuitos trifásicos.

1. 1.REVISÃO DE SEP
1.1.FASORES
Levando-se em conta a identidade de Euller, dada por:
onde: .
Pode-se expressar uma senóide da seguinte maneira:
onde Imag representa a parte imaginária.
Considere agora um sinal senoidal da forma:
Ele pode ser expresso por:
onde representa o FASOR do sinal r(t) e é dado por:
R representa o módulo e o ângulo do fasor .
1.2.IMPEDÂNCIA COMPLEXA
 Parte Real de  Resistência (R);
 Parte Imaginária de  Reatância (X).
Resistor ZR=R Indutor ZL=jωL Capacitor ZC=-j/ωL
Figura 1 – Impedância dos elementos passivos.
Na Figura 1:
 ω = 2πf;

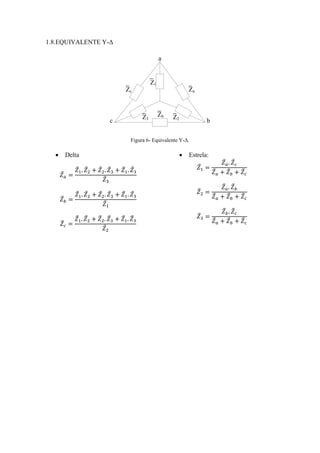
2.  L é a indutância (H);
 C é capacitância (F);
1.3.ADMITÂNCIA COMPLEXA
Onde:
 Parte real de é a condutância  Re[ ] = G;
 Parte imaginária de é a susceptância  Imag[ ] = B.
1.4.POTÊNCIA COMPLEXA
Tendo os fasores de tensão e de corrente , define-se como
potência complexa:
Assim:
O módulo de é denominado POTÊNCIA APARENTE:
em VA.
Na forma retangular, a potência complexa é dada por:
Onde:
  POTÊNCIA ATIVA em W;
  POTÊNIA REATIVA em VAr.
1.5.FATOR DE POTÊNCIA
Onde ϕ é o ângulo entre a tensão e a corrente.
P
S Q
ϕ
Figura 2 – Triângulo de Potências.

3. 1.6.TENSÕES E CORRENTES EM SISTEMAS TRIFÁSICOS EQUILIBRADOS
REDE
A
(ativa)
REDE
B
(passiva)
Fase A
Fase B
Fase C
Neutro
VAN
VBN
VCN
IA
IN
IC
IB
Figura 3 – Redes trifásicas interligadas por quatro condutores.
 Tensão de fase (ou tensão fase-neutro)  tensão existente entre qualquer
condutor fase e o neutro (exemplo: );
 Tensão de linha (ou tensão fase-fase)  tensão existente entre duas fases
(exemplo: );
 Corrente de linha  corrente que circula entre as duas redes (exemplo:
);
 Corrente de fase  corrente que circula em cada impedância que compõem a
carga (depende do tipo de ligação);
 Corrente de neutro  corrente que circula pelo neutro.
Observações:
 Seqüência direta ou positiva de fases: a,b,c;
 Seqüência inversa ou negativa de fases: a,c,b.
1.6.1.Ligação em Estrela (Y)
ZY ZY
ZY
N
A
B
C
IA
IB
IC
IN
Figura 4 – Ligação em estrela.

4.  Tensões de fase (fase A como referência):
 Tensões de linha:
 Corrente de neutro:
 Diagrama fasorial:
1.6.2.Ligação em Delta (Δ)
ZΔ ZΔ
ZΔ
IA
IB
IC
IAB
IBC
ICA
A
B
C
Figura 5 – Ligação em Delta.

5.  Tensões:
 Correntes de fase:
 Correntes de linha:
 Diagrama fasorial das correntes (considerar IAB como referência):
1.7.VALORES EM POR UNIDADE (p.u)
 Para circuitos monofásicos:

6. Logo:
Tem-se ainda que:
 Para circuitos trifásicos:
Logo:
E:
 Mudança de Bases (Impedância):

7. 1.8.EQUIVALENTE Y-Δ
Z3 Z2
Z1
Zc Za
Zb
a
c b
Figura 6- Equivalente Y-Δ.
 Delta
 Estrela: