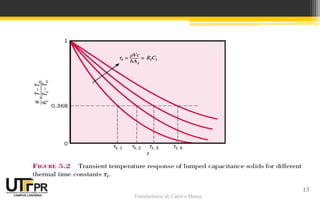
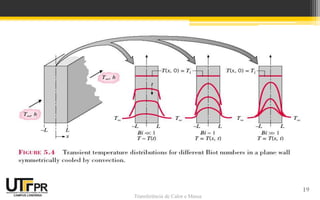
O documento discute conceitos de transferência de calor em regime transiente, incluindo o método da capacitância global, sua validade e aplicações. O método assume que a temperatura no sólido é uniforme no espaço e depende apenas do tempo, o que é válido para números de Biot e Fourier pequenos.

1. Transferência de Calor e
Massa
Prof. Dr. Lucas Freitas Berti
Engenharia de Materiais - UTFPR
lenberti@gmail.com
1

2. Aula 6
Condução em Regime
Transiente
Parte 1
sexta-feira, 5 de maio de 2023

3. Transferência de Calor e Massa
Presença
Cobrança da presença
3

4. Transferência de Calor e Massa
Sumário da aula
 O Método da Capacitância Global
 Validade do Método da Capacitância Global
 Análise Geral Via Capacitância Global
 Efeitos Espaciais
4
 Ementa

5. Transferência de Calor e Massa
O Método da
Capacitância Global
5/34

6. Transferência de Calor e Massa
Transferência de Calor e Massa
 Até agora:
▫ Unidimensional, estacionário, sem geração;
▫ Multidimensional, estacionário, com geração;
 Transiente:
▫ Não-estacionário,
 Condições de contorno mudam com o tempo;
 Tsup ou Tviz muda com o tempo até temperaturas
constantes serem atingidas;
6

7. Transferência de Calor e Massa
Transferência de Calor e Massa
 Um lingote removido e exposto ao ar
1. Energia transferida por convecção e radiação;
2. Condução ocorrerá do interior para a superfície;
 Isso ocorrerá até as temperaturas ficarem constantes
no sistema todo
▫ As propriedades finais serão modificadas de acordo
com o histórico térmico no tempo que o lingote é
submetido
7

8. Transferência de Calor e Massa
Um problema simples e comum de condução transiente
envolve um sólido que passa por uma súbita mudança
no seu ambiente térmico.
8

9. Transferência de Calor e Massa
A essência do Método da Capacitância Global é a
hipótese de que a temperatura do sólido é uniforme no
espaço, em qualquer instante durante o processo
transiente. (Essa hipótese implica que os gradientes de
temperatura no interior do sólido sejam desprezíveis.)
Esta condição é válida se a resistência térmica à
condução no interior do sólido for pequena em
comparação à resistência térmica à transferência de
calor entre o sólido e a sua vizinhança.
9

10. Transferência de Calor e Massa
Como não podemos utilizar a Equação do Calor para
analisar o problema (ausência de gradientes de
temperatura no interior do sólido), a resposta transiente
da temperatura é determinada pela formulação de um
balanço global de energia no sólido.
ou ainda,
dt
dE
E
E ac
ac
sai 

 

 
dt
dT
V
c
T
T
hA p
s 


 
10

11. Transferência de Calor e Massa
A partir da condição inicial, t = 0 e T(0) = Ti , tem-se que
Este resultado indica que a diferença entre as temperaturas
do sólido e do fluido devem diminuir exponencialmente
para zero à medida que t se aproxima do infinito.
 
 























t
V
p
c
s
hA
i
i
e
T
T
T
T 


11

12. Transferência de Calor e Massa
Nesta equação, também fica evidente que a grandeza
(ρcpV/hAs) pode ser interpretada como uma constante
de tempo térmica representada por
sendo que Rt é a resistência térmica à transferência de
calor por convecção e Ct é a capacitância térmica
global do sólido.
  t
t
p
s
t C
R
V
c
hA









 

1
12

13. Transferência de Calor e Massa
13

14. Transferência de Calor e Massa
Qualquer aumento em Rt ou em Ct causará uma
resposta mais lenta do sólido a mudanças no seu
ambiente térmico.
O total da energia transferida Q até algum instante de
tempo t, é expresso por
e ainda,
 
s
p t
hA t
t t t t
c V
s s i p i
0 0 0
Q qdt hA dt hA T T e dt c V 1 e
 
   

 
  
 
 

  
 
   

 
 
        
 
 
  
Q
Eac 


14
 
dt
dT
V
c
T
T
hA p
s 


 

15. Transferência de Calor e Massa
Validade do Método
da Capacitância Global
15

16. Transferência de Calor e Massa
O Método do Capacitância Global é o método mais
simples e conveniente que pode ser utilizado na
solução de problemas transientes de aquecimento e
resfriamento.
Desta forma, é importante determinar sob quais
condições ele pode ser empregado com precisão
satisfatória.
16

17. Transferência de Calor e Massa
ou ainda,
conv
cond q
q 
   



 T
T
hA
T
T
L
kA
,
s
,
s
,
s 2
2
1
 
 
1 2
2
1
s, s, t ,cond
t ,conv
s,
L
T T R hL
kA
Bi
R k
T T
hA

 
 
  
   
 

 
 
17

18. Transferência de Calor e Massa
O número de Biot (Bi) desempenha um papel fundamental
nos problemas de condução que envolvem efeitos
convectivos nas superfícies.
Este parâmetro adimensional fornece uma medida da
queda de temperatura no sólido em relação à diferença
de temperaturas entre a superfície e o fluido.
Se Bi << 1, a resistência térmica à condução no interior do
sólido é muito menor do que a resistência térmica à
convecção através da camada-limite no fluido.
18

19. Transferência de Calor e Massa
19

20. Transferência de Calor e Massa
Para este problema transiente, para Bi << 1, o gradiente
de temperatura no sólido é pequeno e T(x,t) ~ T(t).
Virtualmente, toda a diferença de temperaturas está
entre o sólido e o fluido, e a temperatura do sólido
permanece praticamente uniforme à medida que
diminui para T∞ .
Para valores do número de Biot de moderados para
elevados, os gradientes de temperatura no interior do
sólido são significativos, ou seja, T = T(x,t).
20

21. Transferência de Calor e Massa
Na análise de problemas transientes de aquecimento e
resfriamento, se
o erro associado à utilização do Método da Capacitância
Global é pequeno. Por conveniência, o comprimento
característico, Lc , foi definido como
1
0,
k
hL
Bi c


s
c
A
V
L 
21

22. Transferência de Calor e Massa
Com isso, nota-se que
sendo que,
é conhecido por número de Fourier. Este parâmetro
adimensional é um tempo adimensional que, com o
número de Biot, caracteriza problemas de condução
transiente.
Fo
.
Bi
L
t
k
hL
t
L
L
k
k
L
c
h
t
V
c
hA
c
c
c
c
c
p
p
s



















2



2
c
L
t
Fo


22

23. Transferência de Calor e Massa
Finalmente,
se
e
então
 
 
 
Fo
.
Bi
i
i
e
T
T
T
T 








23
 
 























t
V
p
c
s
hA
i
i
e
T
T
T
T 


Fo
.
Bi
L
t
k
hL
t
L
L
k
k
L
c
h
t
V
c
hA
c
c
c
c
c
p
p
s



















2




24. Transferência de Calor e Massa
Análise Geral Via
Capacitância Global
24

25. Transferência de Calor e Massa
A condução em regime transiente num sólido pode ser
induzida por outros processos além da transferência de
calor por convecção para ou de um fluido adjacente.
Considere a situação na qual as condições térmicas no
interior de um sólido podem ser influenciadas
simultaneamente pela convecção, pela radiação térmica,
pela aplicação de um fluxo em sua superfície e pela
geração interna de energia.
25

26. Transferência de Calor e Massa
A figura mostra uma condição térmica sendo influenciada
por convecção, radiação, fluxo de calor aplicado à
superfície e geração interna de energia
dt
dE
E
E
E
E ac
ac
g
sai
ent 


 



26

27. Transferência de Calor e Massa
   
s s,h conv rad g p
s c,r
dT
q A q q A E c V
dt
  
    
ou ainda,
Esta equação é uma EDO não-linear de primeira ordem,
não-homogênea, que não pode ser integrada para
obtenção de uma solução exata.
   
   
dt
dT
V
c
E
A
T
T
T
T
h
A
q p
g
r
c
s
viz
h
s
s 
 






 

,
4
4
,
27

28. Transferência de Calor e Massa
Entretanto, soluções exatas podem ser obtidas para
versões simplificadas dessa EDO (seção 5.10).
Por exemplo, para o problema transiente num sólido
envolvendo somente a transferência de calor por
radiação térmica, a EDO se reduz a
 
4
4
, viz
r
s
p T
T
A
dt
dT
V
c 

 


28

29. Transferência de Calor e Massa
Separando variáveis e integrando da condição inicial até
um determinado instante de tempo t, tem-se que
resolvendo estas integrais, o tempo necessário para
alcançar a temperatura T se torna
  
 

t
p
r
s
T
T viz
dt
V
c
A
T
T
dT
i 0
,
4
4 









































 

viz
i
viz
i
viz
i
viz
viz
viz
viz
r
s
p
T
T
T
T
T
T
T
T
T
T
T
T
T
A
V
c
t 1
1
3
,
tan
tan
2
ln
ln
4 


29

30. Transferência de Calor e Massa
Esta expressão não pode ser utilizada para determinação
de T de forma explícita em função de t, Ti e Tviz , muito
menos ser simplificada para o resultado limite quando
Tviz = 0 (radiação para o espaço infinito).
30







































 

viz
i
viz
i
viz
i
viz
viz
viz
viz
r
s
p
T
T
T
T
T
T
T
T
T
T
T
T
T
A
V
c
t 1
1
3
,
tan
tan
2
ln
ln
4 



31. Transferência de Calor e Massa
Entretanto, se antes da realização da integração da EDO
simplificada, fosse considerado que Tviz = 0, sua
solução fornecerá









 3
3
,
1
1
3 i
r
s
p
T
T
A
V
c
t



31







































 

viz
i
viz
i
viz
i
viz
viz
viz
viz
r
s
p
T
T
T
T
T
T
T
T
T
T
T
T
T
A
V
c
t 1
1
3
,
tan
tan
2
ln
ln
4 


 
i
T t
s,r
4
p
T 0
A
dT
dt
c V
T
 



 
  
 

t
p
r
s
T
T viz
dt
V
c
A
T
T
dT
i 0
,
4
4 



32. Transferência de Calor e Massa
Uma outra simplificação do problema, ser o caso em que
a radiação térmica fosse desprezada e o coeficiente
convectivo h fosse independente do tempo. Neste
caso, a EDO simplificada que representada a
conservação da energia será expressa por
 
s s,a s,c g p
dT
q A hA T T E c V
dt


    
32

33. Transferência de Calor e Massa
Considerando que θ ≡ T – T∞ , esta equação pode ser
escrita como uma EDO linear de primeira ordem não-
homogênea
sendo que,
0


 b
a
dt
d


V
c
hA
a
p
c
s

,
  
V
c
E
A
q
b
p
g
h
s
s






,
33

34. Transferência de Calor e Massa
Embora esta equação possa ser resolvida pela soma das
suas soluções homogênea e particular, uma
abordagem alternativa é eliminar a não-
homogeneidade pela introdução da transformação
com isso,
b
a
 
  
0
d
a
dt




 
34

35. Transferência de Calor e Massa
Separando variáveis e integrado do 0 até t (θi' até θ'),
segue-e que
com isso,
ou,
0
i
t
d
a dt







 

 
i
ln at



 

at
i
e






35

36. Transferência de Calor e Massa
Portanto, substituindo-se as definições de θ' e θ, a
solução da equação será expressa por
Note que quando b = 0, esta equação se reduz a mesma
forma da solução do problema envolvendo somente
transferência de calor por convecção.
 
at
i
at
i
e
T
T
a
b
e
T
T
T
T 










1
36
 
 
s
p
hA
t
c V Bi*Fo
i i
T T
e e
T T
 
 

 
 
 

  
  
 



  
 

37. Transferência de Calor e Massa
Outro fato interessante, é que no limite de t → ∞, esta
solução transforma-se em (T – T∞) = b/a, resultando
no que poderia também ser obtido por um balanço de
energia, em condições de regime permanente, na
superfície de controle do nosso problema.
  0
,
, 




  g
c
s
h
s
s E
T
T
hA
A
q 
0


 g
sai
ent E
E
E 


37
V
c
hA
a
p
c
s

,

 
V
c
E
A
q
b
p
g
h
s
s






,
 
at
i
at
i
e
T
T
a
b
e
T
T
T
T 










1

38. Transferência de Calor e Massa
Efeitos
Espaciais
38

39. Transferência de Calor e Massa
Quando o Método da Capacitância Global não puder
ser utilizado (Bi ≥ 0,1) para a solução de problemas
de condução em regime transiente, abordagens
alternativas devem ser utilizadas considerando a
existência de gradientes de temperatura no interior do
meio.
A solução da EDP apropriada do problema fornece a
variação da temperatura com o tempo e com as
coordenadas espaciais.
39

40. Transferência de Calor e Massa
Considere o problema de condução 1D em regime
transiente sem geração interna e com propriedades
termofísicas constantes numa parede plana.
40

41. Transferência de Calor e Massa
A Equação do Calor deste problema é expressa por
A condição inicial é .
E as condições de contorno são
t
T
x
T






1
2
2
  i
T
x
T 
0
,
0
0




x
x
T
 
 






 T
t
L
T
h
x
T
k
L
x
,
41

42. Transferência de Calor e Massa
Destas equações fica evidente que, além de serem funções
de x e de t, as temperaturas na parede também dependem
de uma série de parâmetros físicos.
Neste ponto, é importante ressaltar a vantagem da
adimensionalização destas equações. Para tal, considere
que
 
h
k
L
T
T
t
x
f
T i ,
,
,
,
,
,
, 








T
T
T
T
i
i


*
L
x
x 
* 2
*
L
t
Fo
t



42

43. Transferência de Calor e Massa
Com isso, a Equação do Calor e as condições inicial e
de contorno adimensionalizadas são expressas por
sendo que, Bi é o número de Biot.
Fo
x 



 *
*
*
2
2


  1
0
*,
* 
x

0
*
*
0
*




x
x

 
Fo
Bi
x x
,
1
*
*
*
1
*







43
t
T
x
T






1
2
2
  i
T
x
T 
0
,
0
0




x
x
T
 
 






 T
t
L
T
h
x
T
k
L
x
,






T
T
T
T
i
i


*
L
x
x 
*
2
*
L
t
Fo
t




44. Transferência de Calor e Massa
Na forma adimensional, a dependência funcional pode
ser representada como
Antes
Ressalta-se que uma dependência funcional semelhante,
sem a variação com x*, foi obtida para o Método da
Capacitância Global.
 
Bi
Fo
x
f ,
*,
* 

44
 
h
k
L
T
T
t
x
f
T i ,
,
,
,
,
,
, 



45. Transferência de Calor e Massa
Soluções analíticas exatas para problemas de condução
transiente foram obtidas para muitas geometrias e
condições de contorno simples e estão disponíveis na
literatura.
Tipicamente a solução da distribuição de temperaturas
adimensional tem a forma de uma série infinita.
Contudo, exceto para valores muito pequenos do
número de Fourier, essa série pode ser aproximada por
um único termo.
45

46. Transferência de Calor e Massa
Próxima aula
 A Parede Plana com Convecção
▫ Solução Exata
▫ Solução Aproximada
▫ Transferência Total de Energia
 Sistemas Radiais com Convecção
▫ Soluções Exatas
▫ Soluções Aproximadas
▫ Transferência Total de Energia
 O Sólido Semi-Infinito
46
 Ementa

47. Transferência de Calor e Massa
Fonte Bibliográfica
 INCROPERA, F.P., DEWITT, D.P., BERGMAN, T.L. &
LAVINE, A.S., 2008. Fundamentos de Transferência de
Calor e de Massa. Rio de Janeiro, RJ: LTC, 643p.
47