Este documento discute métodos numéricos para determinar zeros reais de funções reais. É dividido em três seções: 1) Isolamento de raízes, que trata da análise teórica e gráfica da função para isolar intervalos contendo cada raiz; 2) Refinamento de raízes, que apresenta métodos iterativos como a bisseção para refinar as aproximações das raízes; e 3) Critérios de parada para os métodos iterativos.

1. Zeros Reais de Funções
Reais
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

2. Programa
g
1. Introdução
2. Isolamento d raízes
2 I l
das í
3. Refinamento
a) Critério de parada
b) Métodos iterativos
c) Comparação entre os métodos

3. Zeros Reais de Funções
Reais – Introdução
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

4. Zeros de funções reais - Introdução
ç
ç

Necessidade de resolução de equações do tipo f(x) = 0
Estruturas
F
Circuitos
i
R
+FV
Em cada nó
+FH :
-FH
-FV
 FH = 0
 FV = 0
+
v = g(i)
E
E - Ri – g(i) = 0
(Lei de Kirchhoff)

5. Zeros de funções reais - Introdução
ç
ç

 é um zero da função f(x) ou raiz da equação

Zeros podem ser reais ou complexos.

Este capítulo trata de zeros reais de f(x).
f(x)
f( ) = 0 se f() = 0
0.

Abscissas dos pontos onde a curva intercepta o eixo x
p
p
f(x)
1
2
x

6. Zeros de funções reais - Introdução
ç
ç

Para uma equação de segundo grau na forma:
ax 2  bx  c  0

Determinação das raízes em função de a, b e c:
x  b  b 2  4ac
2a

Polinômios de grau mais elevado e funções com maior
grau de complexidade


Impossibilidade de determinação exata dos zeros
Uso de soluções aproximadas

7. Zeros de funções reais - Introdução
ç
ç

Etapas para a determinação de raízes a partir de
métodos numéricos
é d
éi

FASE 1: Determinação de um inter alo (o menor possí el)
1
m intervalo
possível)
que contenha apenas uma raiz

FASE 2: Melhoramento do valor da raiz aproximada
(refinamento até que a raiz esteja dentro uma precisão ε
prefixada)

8. Zeros Reais de Funções
Reais – Isolamento de Raízes
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

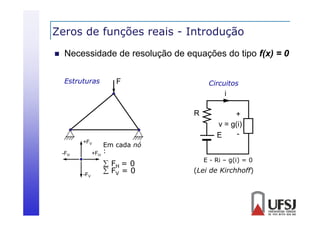
9. Isolamento de raízes

Realização de uma análise teórica e gráfica da função
f(x)
f( )

Precisão das análises é relevante para o sucesso da
fase posterior

Teorema 1
Sendo f(x) contínua em um intervalo [a, b], se f(a)f(b) < 0
então existe pelo menos um ponto x =  entre a e b que é
zero de f(x).

10. Isolamento de raízes – Análise Gráfica
f(x)
( )
f(x)
a

b
a
x
2
1
f(x)
a
1
2
b
x
3b
x

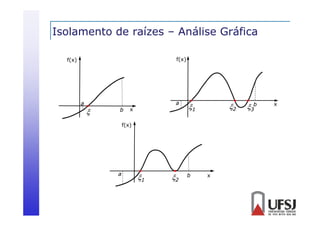
11. Isolamento de raízes – Tabelamento

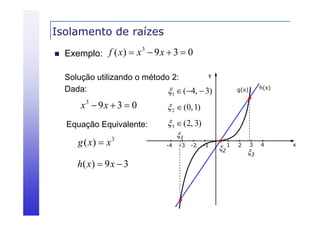
f ( x)  x 3  9 x  3
Exemplo:
f(x) é contínua para  x  
I1 = [-5, -3]
I2 = [0, 1]
I3 = [2, 3]
Cada um dos intervalos acima contém pelo menos um
zero de f(x).

12. Isolamento de raízes – Tabelamento

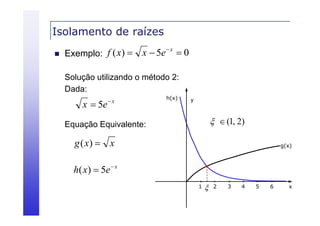
Exemplo: f ( x) 
x  5e  x
f(x) admite pelo menos um zero no intervalo [1 2]
[1,2]
Mas esse zero é único?
Análise do sinal de f’(x)
1
f ' ( x) 
 5e  x  0,  x  0
2 x

f(x) admite um único zero em todo seu domínio
de definição, localizado no intervalo [1,2]

13. Isolamento de raízes

A partir do Teorema 1, se f’(x) existir e preservar o sinal
em ( b) então esse i
(a,b),
intervalo contém um ú i zero d
l
é
único
de
f(x)

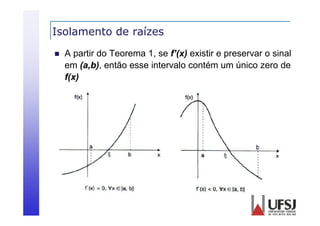
14. Isolamento de raízes

Se f(a)f(b) > 0, então se pode ter diversas situações no
intervalo [ b]
i
l [a, b].

15. Isolamento de raízes

A análise gráfica é fundamental para se obter boas
aproximações para a raiz
i
i

Suficiente utilizar um dos seguintes passos:

Esboçar o gráfico de f(x)

Localizar as abscissas dos pontos onde a curva intercepta o
eixo x

Obtenção da equação equivalente g(x) = h(x) a partir da
equação f(x) = 0

Construção dos gráficos de g(x) e h(x) no mesmo sistema
cartesiano e localização dos pontos x nos quais g(x) e h(x)
se interceptam (f() = 0  g() = h() )

Uso de programas para traçar gráficos de funções

16. Isolamento de raízes

O esboço do gráfico de uma função requer um estudo
detalhado de
d lh d d seu comportamento, no qual d
l devem ser
considerados os itens abaixo:






Domínio da f nção
função
Pontos de descontinuidade
Intervalos de crescimento e decrescimento
Pontos de máximo e mínimo
Concavidade
Pontos de inflexão, etc

17. Isolamento de raízes

f ( x)  x 3  9 x  3
Exemplo:
1  (4,  3)
Solução utilizando o método 1:
f ( x)  x 3  9 x  3
 2  (0, 1)
f(x)
 3  (2, 3)
f ' ( x)  3x 2  9
f ' ( x)  0  x   3
x
f(x)
-25
-4
4
25
-3
3
-  3 13,3923
-1
11
0
3
1
-5
 3 -7,3923
2
-7
3
3
1
-4
-3
2
-2
-1
1
3
2
3
4
x

18. Isolamento de raízes

f ( x)  x 3  9 x  3  0
Exemplo:
y
Solução utilizando o método 2:
Dada:
Dada
1  (4,  3)
x3  9 x  3  0
 2  (0, 1)
Equação Equivalente:
h(x)
g(x)
 3  (2, 3)
g ( x)  x
3
h( x )  9 x  3
1
-4
-3
-2
-1
2 1
2
3
3
4
x

19. Isolamento de raízes

f ( x)  x  5e  x  0
Exemplo:
Solução utilizando o método 2:
Dada:
Dada
x  5e
x
h(x)
y
  (1, 2)
Equação Equivalente:
g ( x)  x
g(x)
h( x)  5e  x
1

2
3
4
5
6
x

20. Isolamento de raízes

Exemplo: f ( x)  x log( x)  1  0
Solução utilizando o método 2:
Dada:
Dada
y
1
log( x) 
x
  (2, 3)
h(x)
Equação Equivalente:
g ( x)  l ( x)
log(
1
h( x ) 
x
g(x)
1
2

3
4
5
6
x

21. Zeros Reais de Funções
Reais – Refinamento de Raízes
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

22. Refinamento de raízes

Aplicação de métodos numéricos destinados ao
refinamento d raízes
fi
de í
I.
II.
II
III.
IV.
IV
V.
Método da Bisseção
Método da Posição Falsa
Método do Ponto Fixo
Método de Newton-Raphson
Método da Secante

Diferenciação dos métodos  Modo de refinamento

Método Iterativo  Caracterizado por uma série de
instruções executáveis seqüencialmente, algumas das
quais repetidas em ciclos (iterações)

23. Refinamento de raízes
Sequência de passos:

24. Critérios de Parada

Teste: xk suficientemente próximo da raiz exata?

Como verificar tal questionamento?

Interpretações para raiz aproximada


x é raiz aproximada com precisão  se:
ou f (x)  
x   
Como proceder se não se conhece  ?

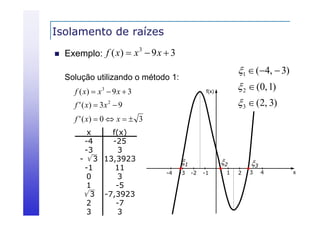
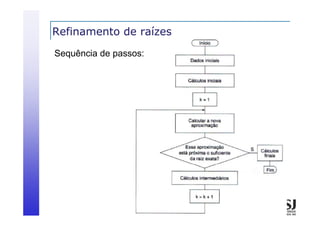
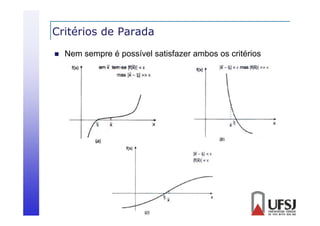
25. Critérios de Parada

Redução do intervalo que contém a raiz a cada iteração

Obtenção de um intervalo [a,b] tal que:
  a, b


e.  então  x  a, b  , x    
ba 



Logo  x  a, b

pode ser tomado como x

26. Critérios de Parada

Nem sempre é possível satisfazer ambos os critérios

27. Critérios de Parada

Métodos numéricos devem satisfazer a pelo menos um dos
critérios

Quando
Q ando da utilização de programas comp tacionais
tili ação
computacionais,
devemos utilizar:

Teste de Parada

Estipular o número máximo de iterações

Prevenção de loops por:

Erro no programa

Escolha de método inadequado

28. Zeros Reais de Funções
Reais – Método da Bisseção
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

29. Método da Bisseção
ç

Dada uma função f(x) contínua no intervalo [a,b] onde
existe uma raiz ú i
i
i única, é possível d
í l determinar tal raiz
i
l i
subdividindo sucessivas vezes o intervalo que a
contém pelo ponto médio de a e b
b.

Em
E outras palavras, o objetivo d
l
bj i deste método é reduzir
é d
d i
a amplitude do intervalo que contém a raiz até atingir
precisão requerida, bk  ak   ou f (x)   , usando
requerida
para isto a sucessiva divisão de [a,b] ao meio

30. Método da Bisseção
ç

Definição do intervalo inicial

Atribui-se [a,b] como intervalo inicial



a0 = a
b0 = b
Condições de Aplicação

f(a) x f(b) < 0

Sinal da derivada constante

31. Método da Bisseção
ç

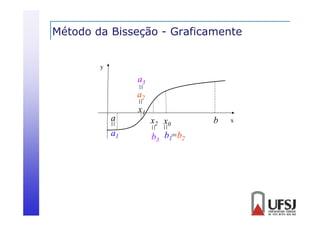
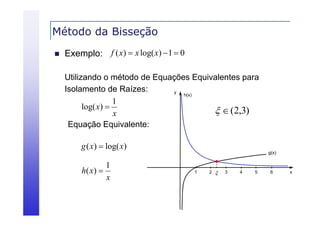
Definição de novos intervalos

Calcula-se o ponto médio entre a e b, chamado de x0

Determina-se qual o subintervalo – [a , x0] ou [x0 , b] –
contém a raiz

Calcula-se o produto f(a) * f(x0)

Verifica-se f(a) * f(x0) < 0
  (a, x0 )
 Se verdadeiro


Caso contrario


Logo a = a e b = x0
  ( x0 , b)
Logo a = x0 e b = b
Repete se
Repete-se o processo até que o valor de x atenda
às condições de parada.

32. Método da Bisseção - Resumo
ç
a0  b0
2
 f ( a0 )  0 


f (b0 )  0 

 f ( x )  0
0


  (a0 , x0 )

 a1  a0
b  x
0
1
a1  b1
x1 
2
 f (a1 )  0


 f (b1 )  0 
 f ( x )  0
1


  ( x1 , b1 )

 a2  x1
b  b
 2 1
a2  b2
x2 
2
 f ( a2 )  0 


f (b2 )  0 

 f ( x )  0
2


  ( x2 , b2 )

 a3  x2
b  b
2
 3
x0 



33. Método da Bisseção - Graficamente
ç
y
a3
||
a2
||
a
||
a1
x1
x2 x0
||
||
b3 b1=b2
b
x

34. Método da Bisseção
ç

Exemplo: f ( x)  x log( x)  1  0
Utilizando o método de Equações Equivalentes para
Isolamento de Raí es
Raízes:
y
h(x)
1
log( x) 
  (2,3)
x
Equação Equivalente:
g ( x)  log( x)
1
h( x ) 
x
g(x)
1
2

3
4
5
6
x

35. Método da Bisseção
ç

Exemplo: f ( x)  x log( x)  1  0
  (2.5, 3)
 f (2)  0.3979  0

23

  a  x  2,5
 2.5  f (3)  0.4314  0
x0 
 1
0

2
b  b  3
 f (2.5)  5.15  10 3  0
1 0


  (2.5, 2.75)
 f (2.5)  0

2,5  3

  a  a  2,5
x1 
 2.75  f (3)  0
 2
1

2
b  x  2,75
 f (2,75)  0,2082  0
1
 2





36. Método da Bisseção - Algoritmo
ç
g
k = 0;
a0 = a; b0 = b;
xk = (ak + bk)/2;
while bk  ak   and f ( xk )  
hile
if f(ak)f(xk) < 0 then
/*raiz em [ak , xk] */
ak+1 = ak;
bk+1 = xk;
else /* raiz em [xk, bk] */
/
/
ak+1 = xk;
bk+1 = bk ;
k 1
end if
xk+1 = (ak+1 + bk+1)/2;
k = k +1;
end while

37. Método da Bisseção - Algoritmo
ç
g

Ao final da execução do algoritmo, teremos um intervalo
[a
[ k, bk] que contém a raiz e uma aproximação x para a
é
i
i
raiz exata (tal que bk  ak   ou f (x)   )

A convergência do método é intuitiva

38. Método da Bisseção – Execução Algoritmo
ç
ç
g

3
Exemplo: f ( x)  x  9 x  3  0
Utilizando o método de Equações Equivalentes para
Isolamento de Raí es
Raízes
1  (4,  3)
x3  9 x  3  0
 2  (0, 1)
Equação Equivalente
 3  (2, 3)
g ( x)  x 3
h( x )  9 x  3

39. Método da Bisseção – Execução Algoritmo
ç
ç
g

3
f ( x)  x 3  9 x  3  0 I  0, 1   3 10
Exemplo:
Cálculo da 1ª aproximação


x0 = (a0+b0)/2 = (0+1)/2 = x0 = 0 5
0,5
f(x0) = 0,53 – 9x0,5 + 3 = -1,375
Teste de Parada

|b a|
|b-a| = |1| > 10-3 e |f(x0)| = |-1,375| = 1,375 > 10-3
| 1,375|
Escolha do Novo Intervalo



f(a0) = 03 – 9x0 + 3 = 3, logo f(a0) > 0
f(b0) = 13 – 9x1 + 3 = -5, logo f(b0) < 0
f(x0) = 0,53 – 9x0,5 + 3 = -1,375, logo f(x0) < 0

logo: a1=a0=0 e b1=x0=0,5

40. Método da Bisseção – Execução Algoritmo
ç
ç
g

3
f ( x)  x 3  9 x  3  0 I  0, 1   3 10
Exemplo:

Então x  0,337890625 em 9 iterações

f
. (x)   foi atendida, enquanto bk  ak   , não foi

41. Método da Bisseção – Estimativa do
número de iterações
ú
d i
õ

Após n iterações, a raiz estará contida no intervalo:
bk 1  ak 1 b0  a0
bk  ak 

2
2k

Deve-se obter o valor de k, tal que bk  ak   , ou seja:
b0  a0

k
2
 2 

k
k
b0  a0

 k log(2)  log(b0  a0 )  log( )

log(b0  a0 )  log( )
log(2)

42. Método da Bisseção – Estimativa do
número de iterações
ú
d i
õ

Exemplo: Considerando um intervalo [2,3] e ε=10-2,
calcular o numero mínimo de iterações para que
tenhamos bk  ak   (Critério de Parada).
log(b0  a0 )  log( )
k
log(2)
log(3  2)  log(10 2 )
k
log(2)
2
log(1)  2 log(10)
k

 6,64
log(2)
g(
0,3010
k 7

43. Método da Bisseção
ç

Vantagens:




Facilidade de implementação;
Estabilidade e convergência para a solução procurada;
Desempenho reg lar e pre isí el
regular previsível.
Desvantagens



Lentidão do processo de convergência (requer o cálculo
de f(x) em um elevado número de iterações);
b0  a0  3
  k  24,8  k  25
7
  10

Necessidade de conhecimento prévio da região na qual se
encontra a raiz de interesse (nem sempre é possível);
Complexidade da extensão do método para
problemas multivariáveis.

44. Método da Bisseção – Exercício
ç
a) Execute as primeiras 5 iterações do Método da
Bisseção para a f
Bi
função f ( x)  x 3  x  1 , tal que
l
  2 10 3
y
b) Caso a condição de
erro não tenha sido
satisfeita, calcule quantas
iterações ainda seriam
necessárias.
4
3
2
1
-4
-3
-2
-1
0
-1
-2
-3
-4
1
2
3
4
5
x

45. Método da Bisseção – Exercício
ç
a) Execute as primeiras 5 iterações do Método da
3
Bisseção para a f
Bi
função f ( x)  x  x  1 , tal que
l
  2 10 3
Iter.
a
b
f(a)
f(b)
x
f(x )
1
1,000000
2,000000
-1,000000
5,000000
1,500000
0,875000
2
1,000000
1,500000
-1,000000
0,875000
1,250000
-0,296875
3
1,250000
1,500000
-0,296875
0,875000
1,375000
0,224609
4
1,250000
1,375000
-0,296875
0,224609
1,312500
-0,051514
5
1,312500
1,375000
-0,051514
0,224609
1,343750
0,082611
Para a iteração 5 temos:
b  a  1,375  1,3125  0,0625  2 10 3 e
f ( x)  0,082611  2 10 3

46. Método da Bisseção – Exercício
ç
b) Caso a condição de erro não tenha sido satisfeita,
calcule quantas i
l l
iterações ainda seriam necessárias.
i d
i
ái
k
log(b0  a0 )  log( )
g(
g(
log(2)
log(2  1)  log(2 10 3 )
k
log(2)
log(1)  (log 2  3  log 10)
log(2)
log(1)  (log 2  3  log 10) 0  (0,30103  3) 2,69897

k

 8,9658
log(2)
0,30103
0,30103
k
k 9

47. Zeros Reais de Funções
Reais – Método da Posição Falsa
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

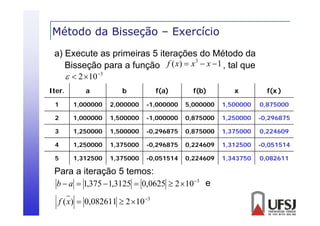
48. Método da Posição Falsa
ç

Método da Bisseção


Calcula a média aritmética dos limites do intervalo que
contém a raiz ([a, b])
Método da Posição Falsa

Calcula a média ponderada dos limites do intervalo que
contém a raiz ([a, b])

49. Método da Posição Falsa
ç

Dada a função f ( x)  x 3  9 x  3  0 e, sendo o intervalo
inicial a, b  0, 1 , temos que f (1)  5  0  3  f (0)



.f (0) está mais próximo de zero que f (1)
Logo é provável que a raiz esteja mais próxima d x = 0
L
á l
i
t j
i
ó i
de
que de x = 1 ( isso é sempre verdade quando f(x) é linear
em a, b )
Assim,
Assim ao invés de tomar a média aritmética o método
aritmética,
da posição falsa toma a média ponderada, com pesos
de f (a) e f (b)
x
a f (b)  b f (a )
f (b)  f (a )

af (b)  bf (a )
f (b)  f (a )

50. Método da Posição Falsa - Graficamente
ç

Graficamente x é a interseção entre o eixo x e a reta
que passa pelos pontos ( f( )) e (b f(b)):
l
(a, f(a)) (b, f(b))

51. Método da Posição Falsa - Graficamente
ç
x1 = a1f(b1) – b1f(a1)
f(x)
x0 = a0f(b0) - b0f(a0)
f(x)
f(b1) - f(a1)
f(b0) - f(a0)
a = a1

x1
a = a0

x0
b = b0
x
b1 = x1
x

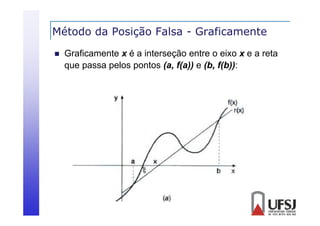
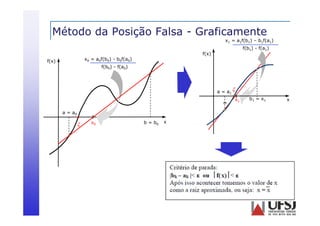
52. Método da Posição Falsa
ç

Definição do intervalo inicial

Atribui-se [a,b] como intervalo inicial



a0 = a
b0 = b
Condições de Aplicação

f(a) x f(b) < 0

Sinal da derivada constante

53. Método da Posição Falsa
ç

Definição dos Subintervalos

Subdivide-se o intervalo pelo ponto de interseção da reta
que liga f(a) a f(b) e o eixo das abscissas
 Verifica-se se, através do teste de parada, se x0 é uma
aproximação da raiz da equação ()  pelo tamanho do
intervalo [a, b] ou o valor f(x0)

Se verdadeiro  x0 é a raiz procurada

Caso contrário  define-se um novo intervalo

54. Método da Posição Falsa
ç

Definição do novo intervalo

Determina-se qual o subintervalo – [a , x0] ou [x0 , b] –
contém a raiz

Calcula-se o produto f(a) * f(x0)

Verifica-se f(a) * f(x0) < 0

Se verdadeiro


Caso contrario


Logo a = a e b = x0
  (a, x0 )
  ( x0 , b)
Logo a = x0 e b = b
g
Repete se
Repete-se o processo até que o valor de x atenda
às condições de parada.

55. Método da Posição Falsa
ç

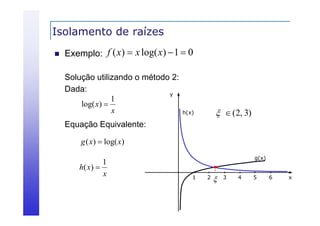
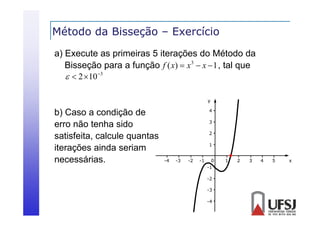
Exemplo: f ( x)  x log( x)  1, I  [2, 3]
f (a0 )  0,3979  0
 logo, existe ao menos 1 raiz no
f (b0 )  0,4314  0  intervalo dado
af (b)  bf (a) 2  0,4314  3  (0,3979) 2,0565
x0 


 2,4798
f (b)  f (a)
0,4314  (0,3979)
0,8293
f ( x0 )  0,0219  0 . Como f (a0 ) e f ( x0 ) têm o mesmo sinal,
a1  x0  2,4798 f (a1 )  0 


f (b1 )  0 
b1  b0  3

56. Método da Posição Falsa
ç

Exemplo: f ( x)  x log( x)  1, I  [2, 3]
a1  x0  2,4798

b1  3
f (a1 )  0 

f (b1 )  0 
af (b)  bf (a) 2,4798  0,4314  3  (0,0219) 1,1354
x1 


f (b)  f (a)
0,4314  (0,0219)
0,4533
x1  2,5049
Como f ( x1 )  0,0011  0 , temos:
a2  x1  2,5049

b2  b1  3
f (a1 )  0 

f (b1 )  0 


57. Método da Posição Falsa - Algoritmo
ç
g
k = 0;
a0 = a; b0 = b
b;
FA0 = f(a0); GB0 = f(b0);
xk = (akGBk - bkFAk) / (GBk - FAk);
while bk  ak   and f ( xk )  
if f(ak)f(xk) ≤ 0 then
/
/* raiz em [ak , xk] */
/
ak+1 = ak;
bk+1 = xk;
else
/* raiz em [xk, bk] */
ak+1 = xk;
bk+1 = bk ;
end if
xk+1 = (ak+1GBk+1 - bk+1FAk+1) / (GBk+1 - FAk+1);
k = k +1;
end while
hile

58. Método da Posição Falsa – Exec. Algoritmo
ç
g

3
f ( x)  x 3  9 x  3  0 I  0, 1   2  10
Exemplo:
Cálculo da
Cál l d 1ª aproximação
i
af (b)  bf (a )
x0 
f (b)  f (a )

0  (5)  1 (3)
3

 0,375
 5  (3)
8
f ( x0 )  (0,375) 3  9  (0,375)  3  -0,322265625
Teste de Parada

|b a|
|b-a| = |1| > 10-3 e |f(x0)| = |-0,322265625| > 10-3
| 0,322265625|
Escolha do Novo Intervalo



f(a0) = 03 – 9x0 + 3 = 3, logo f(a0) > 0
f(b0) = 13 – 9x1 + 3 = -5, logo f(b0) < 0
f(x0) = 0,3753 – 9x0,375 + 3 = -0,32..., logo f(x0) < 0

logo: a1=a0=0 e b1=x0=0,375

59. Método da Posição Falsa – Exec. Algoritmo
ç
g

3
f ( x)  x 3  9 x  3  0 I  0, 1   3  10
Exemplo:
Então x  0,337635046 em 3 iterações
.f (x)   foi atendida, enquanto bk  ak   , não foi
No Método da Bisseção, o valor x  0,337890625 foi
encontrado depois de 9 iterações

60. Método da Posição Falsa
ç

Vantagens:




Estabilidade e convergência para a solução procurada;
Desempenho regular e previsível;
Cálculos
Cálc los mais simples q e o método de Ne ton
que
Newton.
Desvantagens:


Lentidão do processo de convergência (requer o cálculo
de f(x) em um elevado número de iterações);
Necessidade de conhecimento prévio da região na qual se
encontra a raiz de interesse (o que nem sempre é
possível).

61. Zeros Reais de Funções
Reais – Método do Ponto Fixo
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

62. Método do Ponto Fixo

Dada uma função f(x) contínua no intervalo [a,b] onde
existe uma raiz ú i
i
i única, f( ) = 0, é possível transformar tal
f(x) 0
í l
f
l
equação em uma equação equivalente x = φ(x) e, a
partir de uma aproximação inicial x0, gerar uma
sequência {xk} de aproximações para  pela relação xk+1
= φ(xk) uma vez que φ(x) é tal que f() = 0 se e
),
somente se φ() = .

Transformamos o problema de encontrar zero de f(x) no
problema de encontrar um ponto fixo de φ(x)

Af
função φ(x) é chamada d f
ã
( )
h
d de função d it
ã de iteração
ã

63. Método do Ponto Fixo

2
Exemplo: Dada a função f ( x)  x  x  6  0
São funções de iteração possíveis:
1 ( x)  6  x 2
 2 ( x)  6  x
6
3 ( x)   1
x
6
 4 ( x) 
x 1

A forma geral das funções de iteração φ(x) é dada por
 ( x)  x  A( x) f ( x) com a condição de que
A()  0 em , ponto fixo de φ(x)

64. Método do Ponto Fixo

A partir da definição da forma de φ(x),  ( x)  x  A( x) f ( x) ,
podemos então mostrar que f ( )  0   ( )  
d
  seja  tal que f ( )  0
 ( )    A( ) f ( )   ( )   ( porque f ( )  0)
 se  ( )  
   A( ) f ( )    A( ) f ( )  0
 f ( )  0 ( porque A( )  0)

Existem
E istem infinitas eq ações de iteração φ( ) para a
equações
φ(x)
equação f(x) = 0

65. Método do Ponto Fixo - Graficamente

Uma raiz da equação φ(x)=x é a abscissa do ponto de
interseção d reta y=x com a curva y=φ(x)
i
da
( )

66. Método do Ponto Fixo - Graficamente

Todavia, para algumas escolhas de φ(x) o Método do
Ponto Fi pode di
P
Fixo d divergir d valor  procurado
i do l
d

67. Método do Ponto Fixo

Exemplo: Dada a equação f ( x)  x  x  6  0 :
 As raízes são 1 = -3 e 2 = 2 (Não há necessidade de uso
2
de métodos numéricos para o calculo)

Objetivo: Mostrar a convergência ou divergência do processo
iterativo

Seja a raiz 2 = 2 e φ1 (x) = 6 - x2,Tomando x0= 1,5 e φ (x)
= φ1 (x)

Seja a raiz 2 = 2 e  2 ( x)  6  x ,Tomando x0= 1,5 e φ (x)
= φ2 (x)

68. Método do Ponto Fixo

2
Exemplo: Dada a equação f ( x)  x  x  6  0 , com raiz
2 = 2 , φ1 ( ) = 6 - x2 e x0 = 1
(x)
1,5
x1 = φ(x0) = 6 – 1,52 = 3,75
x2 = φ(x1) = 6 – 3,752 = -8,0625
x3 = φ(x2) = 6 – (-8,0625)2 = -59,003906
x4 = φ(x3) = 6 – (-59,003906)2 = -3475,4609
Conclui-se que {xk} não convergirá p
q {
g para 2 = 2

69. Método do Ponto Fixo

2
Exemplo: Dada a equação f ( x)  x  x  6  0 , com raiz
2 = 2 , φ1 ( ) = 6 - x2 e x0 = 1
(x)
1,5
y
Análise Gráfica:
y=x
x2
x1
1
x0 
x
2
{xk}  
φ(x)

70. Método do Ponto Fixo

2
Exemplo: Dada a equação f ( x)  x  x  6  0 , com raiz
2 = 2 ,  2 ( x)  6  x e x0 = 1
1,5
x1 = φ(x0) = 6  1,5  2,121320343
x2 = φ(x1) = 6  2,121320343  1,969436380
x3 = φ(x2) = 6  1,969436380  2,007626364
x = φ(x ) = 6  2,007626364  1,998092499
4
3
x5 = φ(x4) = 6  1,998092499  2,000476818
Conclui-se que {xk} tende a convergir para 2 = 2

71. Método do Ponto Fixo

2
Exemplo: Dada a equação f ( x)  x  x  6  0 , com raiz
2 = 2 ,  2 ( x)  6  x e x0 = 1
1,5
y
Análise Gráfica:
y=x
φ(x)
{xk}  2 quando k  inf
2
x0
x2
x
x1

72. Método do Ponto Fixo
Teorema 2:
Sendo  uma raiz de f(x) = 0, isolada em um intervalo I
centrado em  e φ(x) uma função de iteração para
f(x) = 0. Se
1. φ(x) e φ’(x) são contínuas em I
2. |φ’(x)| < 1,  x  I e
3. x0  I
então a sequencia {xk} gerada pelo processo iterativo xk+1
= φ(xk) convergirá p
φ(
g para  . Além disso quanto menor for
q
o valor de |φ’(x)|, mais rápido o Método do Ponto Fixo
convergirá.

73. Método do Ponto Fixo

Resgatando os exemplos anteriores, para a função
f ( x)  x 2  x  6  0 temos que:


φ1( ) ( 1 ( x)  6  x )  geração de uma sequencia
(x)
ma seq encia
divergente de 2 = 2
2
φ2(x) ( 2 ( x)  6  x )  geração de uma sequencia
convergente para 2 = 2

74. Método do Ponto Fixo

Avaliando a divergência de φ1(x)

φ1(x) = 6 - x2 e φ’1(x) = - 2x  contínuas em I

|φ’1 (x)| < 1  |-2x| < 1  -½ < x < ½

Não existe um intervalo I centrado em 2=2, tal que
|φ (x)|
|φ’(x)| < 1,  x  I  φ1 (x) não satisfaz a
condição 2 do Teorema 2 com relação a 2=2.

75. Método do Ponto Fixo

Avaliando a convergência de φ2(x)



e  2 ' ( x)  (1 / 2 6  x )
φ2 ( ) é contínua em S = {x  R | x  6}
(x)
tí
{


 2 ( x)  6  x
φ
φ’2 (x) é contínua em S’ = {x  R | x < 6}
S
. ' ( x)  1  1 / 2 6  x  1  x  5,75
2
É possível obter um intervalo I centrado em 2=2, tal que
todas as condições do Teorema 2 sejam satisfeitas.

76. Método do Ponto Fixo - Algoritmo
g
 Critérios de Parada

|f(xk)|  

|xk – xk-1|  
k = 0;
x0 = x;
while xk  xk 1   and
k = k +1;
xk+1 = φ(xk);
end while
f ( xk )  

77. Método do Ponto Fixo – Verificando a
Convergência
C
ê i

Exemplo: Dada a função f ( x)  x 2  x  6  0 , cujas raízes
são 2 e -3, vamos avaliar a convergência d f
3
li
ê i da função
equivalente 3 ( x)  6  1 , dados 1 = -3 e x0= -2,5
x
6
 ( x)   1,  x  , x  0
x
6
 ' ( x)  2  0,  x  , x  0
x
6
6
 ' ( x)  2  2 ,  x  , x  0
x
x
6
 ' ( x)  1  2  1  x 2  6  x   6
x
ou
x 6

78. Método do Ponto Fixo – Verificando a
Convergência
C
ê i

Exemplo: Dada a função f ( x)  x 2  x  6  0 , cujas raízes
são 2 e -3, vamos avaliar a convergência d f
3
li
ê i da função
equivalente 3 ( x)  6  1 , dados 1 = -3 e x0= -2,5
x
Como o objetivo é obter a raiz negativa, temos:
I1 tal que  ' ( x)  1, x  I1 , será : I1  (;  6 )
( 6  2,4497897)
Podemos então definir o intervalo I  (3.5,  2.5) que o
processo convergirá visto que o intervalo I  I1 está
centrado na raiz  = -3

79. Método do Ponto Fixo – Verificando a
Convergência
C
ê i

Exemplo: Dada a função f ( x)  x 2  x  6  0 , cujas raízes
são 2 e -3, vamos avaliar a convergência d f
3
li
ê i da função
equivalente 3 ( x)  6  1 , dados 1 = -3 e x0= -2,5
x
Tomando x0= -2,5, temos:
x1  2,5
x2  2,764706
x3  3,170213
x4  2,892617

Quando não se conhece a raiz, escolhe-se o intervalo I
escolhe se
aproximadamente centrado em 
 Quanto mais preciso isolamento de , maior exatidão na
Q
p
escolha de I

80. Método do Ponto Fixo
x3 1
 Exemplo: Dados: f ( x )  x  9 x  3  0;  ( x ) 
 ;
9 3
2
x0  0,5;   5  10 ;   (0, 1) , calcule a raiz de f(x)
3
utilizando o MPF:
Assim, x  0,3376233 e f ( x)  0,12 10 3 , com o mesmo
,
número de iterações que o Método da Posição Falsa.
Importante lembrar: Iteramos de modo que xk 1   ( xk ) ,
todavia avaliamos, a cada iteração, se f ( xk )  
Desafio: Provar que  (x) satisfaz a condição 2 do
Teorema 2 no intervalo (0, 1)

81. Método do Ponto Fixo

Vantagens



Rapidez processo de convergência;
Desempenho regular e previsível.
Desvantagens
g

Um inconveniente é a necessidade da obtenção de uma
função de iteração φ(x);
( )

Difícil sua implementação.

82. Método do Ponto Fixo – Exercício
3
1) Tente encontrar a raiz da função f ( x)  x  x  1
1 1
utilizando a função de iteração  ( x)   2 e x0  1 , sendo
x x
  2 10 3 .Justifique sua resposta.
y
4
3
2
1
-4
-3
-2
-1
0
-1
-2
-3
-4
1
2
3
4
5
x

83. Método do Ponto Fixo – Exercício
3
1) Tente encontrar a raiz da função f ( x)  x  x  1
1 1
utilizando a função de iteração  ( x)   2 e x0  1 , sendo
x x
  2 10 3
1 1
x1 = φ(x0) =  2  2
1 1
1 1
x2 = φ(x1) =  2  0,75
2 2
1
1

 3,1111...
x3 = φ(x2) =
(
2
0,75 0,75
1
1

 0,4247...
x4 = φ(x3) =
2
3,1111 3,1111
1
1

 7,8973...
x5 = φ(x4) =
2
0,4247 0,4247

84. Método do Ponto Fixo – Exercício
3
1) Tente encontrar a raiz da função f ( x)  x  x  1
1 1
utilizando a função de iteração  ( x)   2 e x0  1 , sendo
x x
  2 10 3
1
1

 0,1427...
x6 = φ(x5) =
2
7,8973 7,8973
1
1

 56,1461...
x7 = φ(x6) =
(
2
0,1427 0,1427
Conclui-se que {xk} tende a divergir da raiz da equação f(x).

85. Método do Ponto Fixo – Exercício
3
1) Tente encontrar a raiz da função f ( x)  x  x  1
1 1
utilizando a função de iteração  ( x)   2 e x0  1 , sendo
x x
  2 10 3
Justificando a resposta:
1 2
 x  , x  0  ' ( x)  2  3  x  , x  0
x
x
1 2
x 2
x2
 ' ( x)  1  2  3  1  3  3  1 
1
3
x
x
x
x
x
1 1
 ( x)   2
x x
Como a condição  ' ( x)  1 x  I deve ser satisfeita, onde I
é o intervalo centrado em  , é fácil perceber que isso
não acontece, uma vez que x0  I e  ' ( x0 )   ' (1)  3  0

86. Zeros Reais de Funções
Reais – Método de Newton-Raphson
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

87. Método de Newton-Raphson
p

Método do Ponto Fixo (MPF)



Uma das condições de convergência é que |φ’(x)| < 1,
 x  I , onde I é um intervalo centrado na raiz
A convergência será tanto mais rápida quanto menor for
|φ’(x)|
O método de Newton busca garantir e acelerar a
convergência do MPF
 Escolha de φ(x), tal que φ’() = 0, como função de
iteração

88. Método de Newton-Raphson
p

Dada a equação f(x) = 0 e partindo da forma geral para
φ(x)
( )
φ(x) = x + A(x)f(x)

Busca-se obter a função A(x) tal que φ’() = 0
φ( )
φ(x) = x + A(x)f(x) 
( )( )
φ’(x) = 1 + A’(x)f(x) + A(x)f’(x) 
φ(
φ’() = 1 + A’()f() + A()f’() 
( )(
( ) (
φ’() = 1 + A()f’()

89. Método de Newton-Raphson
p

Assim
1
 ' ( )  0  1  A( ) f ' ( )  0  A( ) 
f ' ( )
1
 donde se toma A( x ) 
f ' ( x)


Como φ(x) = x + A(x)f(x)
Logo:
 1 
 ( x)  x  
 f ' ( x)   f ( x)



 f ( x) 
 ( x)  x  
 f ' ( x) 




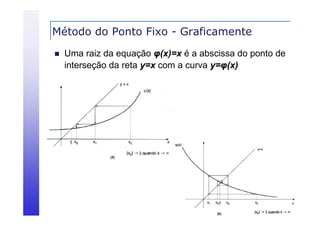
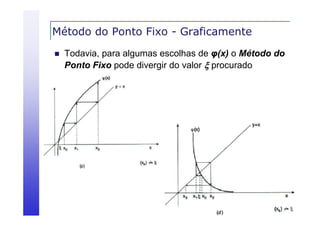
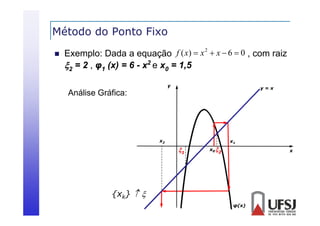
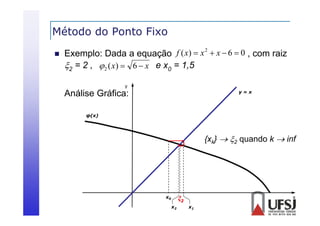
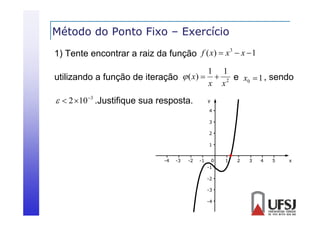
90. Método de Newton-Raphson
p

Então, dada f(x), a função de iteração φ(x) = x - f(x)/f’(x)
será tal que φ’() = 0, posto que
á l
’(
0
 [ f ' ( x)]2  f ( x) f ' ' ( x) 

 ' ( x)  1  
2


[ f ' ( x)]


[ f ' ( x)]2 [ f ' ( x)]2  f ( x) f ' ' ( x)
 ' ( x) 

2
[ f ' ( x)]
[ f ' ( x)]2
f ( x) f ' ' ( x)
 ' ( x) 
[ f ' ( x)]2
e,
e como f() = 0 φ’() = 0 ( desde q e f’()  0 )
0,
que

91. Método de Newton-Raphson
p

Deste modo, escolhido x0, a sequência {xk} será
determinada por
d
i d
f ( xk )
xk 1  xk 
f ' ( xk )
onde k = 0, 1, 2, ...

92. Método de Newton-Raphson –
Graficamente
G fi

Dado o ponto ( xk , f(xk) )
p
(

Traçamos a reta Lk(x) tangente à curva neste ponto:
Lk(x) = f(xk) + f’(xk)(x-xk)

Determinanos o zero de Lk(x), que é um modelo linear
que aproxima f(x) em uma vizinhança xk
f (xk )
(x
Lk ( x)  0  x  xk 
f ' ( xk )

Faz-se xk +1 = x

93. Método de Newton-Raphson –
Graficamente
G fi

Análise Gráfica
f(x)
1a iteração
2a iteração
3a iteração

x0
x3
x2
x1
Repete-se o processo até que o valor de x
atenda às condições de parada.
x

94. Método de Newton-Raphson - Convergência
p
g

Teorema 3:
Sendo f(x), f’(x) e f”(x) contínuas em um intervalo I que
contém uma raiz x =  de f(x) = 0 e supondo f’()  0,
existirá um intervalo Ī  I contendo a raiz , tal que se
x0  Ī a sequencia { k} gerada pela fó
Ī,
i {x
d
l fórmula recursiva
l
i
f ( xk )
xk 1  xk 
f ' ( xk )
convergirá para a raiz.

95. Método de Newton-Raphson
p

Exemplo: Dado f(x) = x2 + x – 6 , 2 = 2 e x0 = 1,5
Fórmula recursiva:
f ( x)
x2  x  6
 x
 ( x)  x 
f ' ( x)
2x 1
x1
1,5
  ( x )  1,5 
x2
2,0625
  ( x )  2,0625 
0
1

 1,5  6
 2,0625
2 1,5  1
2

 2,0625  6
 2,000762195
2  2,0625  1
x3   ( x2 )  2,000000116
2

96. Método de Newton-Raphson
p

Exemplo: Dado f(x) = x2 + x – 6 , 2 = 2 e x0 = 1,5

Comentários:

A parada poderá ocorrer na 3a iteração (x = 2,000000116)
caso a precisão do cálculo com 6 casas decimais for
satisfatória para o contexto do trabalho

Observe que, no Método do Ponto Fixo, com
 ( x)  6  x o valor x = 2,000476818 foi encontrado
somente na 5a iteração

97. Método de Newton-Raphson - Algoritmo
p
g

Teste de parada:
 |f(xk)|  ε
 |xk – xk-1|  ε

Algoritmo:
g
x0 := x;
;
k := 0;
while |f(xk)| > ε and |xk – xk-1| > ε
|(
|
xk+1 := xk – f(xk)/f’(xk)
k := k +1;
;
end while

98. Método de Newton-Raphson - Algoritmo
p
g

Exemplo: Considere a função f(x) = x3 - x - 1, e
ε = 0 002 cujos zeros encontram-se nos i
0,002 j
intervalos:
l
1  I1 = (-1, 0), 2  I2 = (1, 2)
Seja:
x0 = 1
f ( xk )
xk 1  xk 
f ' ( xk )
x3  x 1
 ( x)  x 
3x 2  1

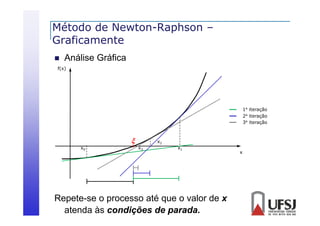
99. Método de Newton-Raphson - Algoritmo
p
g

Exemplo: Considere a função f(x) = x3 - x - 1, e
ε = 0 002 cujos zeros encontram-se nos i
0,002 j
intervalos:
l
1  I1 = (-1, 0), 2  I2 = (1, 2)

Cálculo da 1ª aproximação
1
φ(x0) = 1 – [ (1)³ – 1 – 1 ] = 1,5 = x1
[ 3x(1)² – 1 ]
3 (1)²

Teste de Parada
|f(x1)| = | (1,5)³ – 1,5 – 1 | = 0,875 > 
|x1-x0| =| 1,5 - 1 | = 0,5 > 

100. Método de Newton-Raphson - Algoritmo
p
g

Exemplo: Considere a função f(x) = x3 - x - 1, e
ε = 0 002 cujos zeros encontram-se nos i
0,002 j
intervalos:
l
1  I1 = (-1, 0), 2  I2 = (1, 2)

Cálculo da 2ª aproximação
p
ç
φ(x1) = 1,5 – [ (1,5)³ – 1,5 – 1 ] = 1,3478261 = x2
[ 3x(1,5)² – 1 ]
3x(1 5)²

Teste de Parada
|f(x2)| = | 0,100682 | = 0,100682 > 
|
|x2-x1| =| 1,3478261 - 1,5 | = 0,1521739 > 
| ,
,
,

101. Método de Newton-Raphson - Algoritmo
p
g

Exemplo: Considere a função f(x) = x3 - x - 1, e
ε = 0 002 cujos zeros encontram-se nos i
0,002 j
intervalos:
l
1  I1 = (-1, 0), 2  I2 = (1, 2)

Cálculo da 3ª aproximação
p
ç
φ(x2) = 1,3478261 - [ (1,3478261)³ - 1,3478261 - 1 ]
[ 3x(1,3478261)² - 1 ]
3 (1 3478261)²
φ(x2) = 1,3252004 = x3

Teste de Parada
|(
|f(x3)| =| 0,0020584 | = 0,0020584 > 
|
|x3-x2| =| 1,3252004 – 1,3478261 | = 0,0226257 > 

102. Método de Newton-Raphson - Algoritmo
p
g

Exemplo: Considere a função f(x) = x3 - x - 1, e
ε = 0 002 cujos zeros encontram-se nos i
0,002 j
intervalos:
l
1  I1 = (-1, 0), 2  I2 = (1, 2)
A sequência {xk} gerada pelo método de Newton
será:
Iteração
x
|xk-xk-1|
1
1,5
0,5
2
1,3478261
0,1521739
0,1006822
3
1,3252004
1 3252004
0,0226257
0 0226257
0,0020584
0 0020584
4
1,3247182
0,0004822

= 0,002
F(x)
0,875
1,0352x10-6

103. Método de Newton-Raphson
p

Comprovando o impacto de uma boa escolha de x0

Exemplo: Considere a função f(x) = x3 – 9x + 3, que
possui três zeros: 1  I1 = (-4, -3), 2  I2 = (0, 1) e
3  I3 = (2 3) Seja x0 = 1,5:
(2, 3).

104. Método de Newton-Raphson
p

Comprovando o impacto de uma boa escolha de x0

Exemplo: Considere a função f(x) = x3 – 9x + 3, que
possui três zeros: 1  I1 = (-4, -3), 2  I2 = (0, 1) e
3  I3 = (2 3) Seja x0 = 1,5:
(2, 3).

No início há um divergência da região onde estão as
raízes, mas depois de x7 os valores se aproximam cada
vez mais d 3
i de

Causa:

x0 (1,5) é próximo de

Da mesma forma, x1 (-1,6666667) está próximo
de 
3
3 , outra raiz de f’(x)
, que é raiz de f´(x)

105. Método de Newton-Raphson
p

Vantagens:
Rapidez processo de convergência
 Desempenho elevado


Desvantagens:
Necessidade d obtenção d f’( ) , o que pode ser
N
id d da bt
ã de f’(x)
d
impossível em determinados casos
 O cálculo do valor numérico de f’(x) a cada iteração
f (x)


106. Zeros Reais de Funções
Reais – Método da Secante
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

107. Método da Secante

Método de Newton-Raphson


Um grande inconveniente é a necessidade da obtenção de
f’(x) e o cálculo de seu valor numérico a cada iteração
Forma de desvio do inconveniente

Substituição da derivada f’(xk) pelo quociente das
diferenças
f ( xk )  f ( xk 1 )
f ' ( xk ) 
xk  xk 1

108. Método da Secante

A função de iteração será:
f ( xk )
 ( x )  xk 
f ( xk )  f ( xk 1 )
xk  xk 1
f ( xk )
xk  xk 1 
 ( x )  xk 
f ( xk )  f ( xk 1 )
xk f ( xk )  xk f ( xk 1 ) xk f ( xk )  xk 1 f ( xk )
 ( x) 

f ( xk )  f ( xk 1 )
f ( xk )  f ( xk 1 )
xk 1 f ( xk )  xk f ( xk 1 )
 ( x) 
f ( xk )  f ( xk 1 )

109. Método da Secante - Geometricamente

A partir de duas aproximações xk-1 e xk obtém-se o
ponto xk+1 como sendo a abscissa d ponto d
d
b i
do
de
intersecção do eixo x e da reta que passa pelos pontos
( xk-1 , f(xk-1) ) e ( xk , f(xk) ) (secante à curva da função)
f(x)
1a
2a
3a
4a
x0
x1
x3 x4
x5

x2
iteração
iteração
iteração
iteração
x
Repete-se
Repete se o processo até
que o valor de x atenda às
condições de parada.

110. Método da Secante - Convergência
g

Como o Método da Secante é uma aproximação do
método d N
é d de Newton, as condições d convergência são
di
de
ê i
praticamente as mesmas, ou seja basta que o
Teorema 3 seja satisfeito

Todavia, o Método da Secante pode divergir para o
seguinte caso f ( xk )  f ( xk 1 )
xk 1 f ( xk )  xk f ( xk 1 )
 ( x) 
f ( xk )  f ( xk 1 )

111. Método da Secante

Exemplo: Considere-se a função f(x) = x2 + x – 6 = 0,
x0 = 1 e x1 = 1
1,5
1,7:
Solução:
x0  f ( x1 )  x1  f ( x0 ) 1,5  (1,41)  1,7  2,25

x2 
 1,41  2,25
f ( x1 )  f ( x0 )
x2  2 03571
2,03571
x1  f ( x2 )  x2  f ( x1 )
 1 99774
1,99774
x3 
f ( x2 )  f ( x1 )
x2  f ( x3 )  x3  f ( x2 )
x4 
 1,99999
f ( x3 )  f ( x2 )

112. Método da Secante

Exemplo: Considere-se a função f(x) = x2 + x – 6 = 0,
x0 = 1 e x1 = 1
1,5
1,7:

Comentários:

A parada poderá ocorrer na 3a iteração (x = 1,99999 ),
caso a precisão do cálculo com 5 casas decimais for
satisfatória para o contexto do trabalho

No método de Newton-Raphson o valor
x = 2,000000116, foi encontrado também na 3a
iteração

113. Método da Secante - Algoritmo
g

Testes de Parada
 |f(xk)|  ε
 |xk – xk-1|  ε

Algoritmo
g
x0 := x;
x1 := x1;
k := 1;
while |f(xk)| > ε and |xk – xk-1| > ε
|(
|
xk+1 := (xk-1*f(xk) - xk*f(xk-1)) / (f(xk) - f(xk-1));
k := k +1;
;
end while

114. Método da Secante – Execução Algoritmo
ç
g

Exemplo: Considere-se a função f(x) = x3 - x - 1,
 = 0,003, x0 = 1,5 e x1 = 1,7:
xk 1 f ( xk )  xk f ( xk 1 )
 ( x) 
f ( xk )  f ( xk 1 )

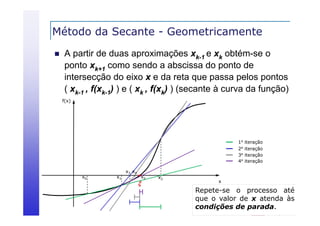
115. Método da Secante – Execução Algoritmo
ç
g

Exemplo: Considere-se a função f(x) = x3 - x - 1,
 = 0,003, x0 = 1,5 e x1 = 1,7:

Cálculo da 1ª aproximação x0 = 1,5 e x1 = 1,7
f(x0) = 0,875 > 0
f(x1) = 2,213 > 0
x2 = [1,5 x (2,213) – 1,7 x (0,875)] = 1,36921
[ ,
( ,
)
,
( ,
)]
,
[2,213 – (0,875)]
 Teste de Parada
|f(x2)| = | (1,36921)³ – 1,36921 – 1 | = 0,19769 > 
|x2 - x1| =|1,36921 – 1 7| = 0 33079 > 
=|1 36921 1,7| 0,33079
 Novo Intervalo: x1 = 1,7 e x2 = 1,36921

116. Método da Secante – Execução Algoritmo
ç
g

Exemplo: Considere-se a função f(x) = x3 - x - 1,
 = 0,003, x0 = 1,5 e x1 = 1,7:
Cálculo da 2ª aproximação x1 = 1,7 e x2 = 1,36921
f(x1) = 2,213 > 0
f(x2) = 0,19769 > 0
x3 = [1,7 x (0,19769) - 1,36921x (2,213)] = 1,33676
[0,19769 - 2,213]
 Teste de Parada

|f(x3)| = |0,05193| = 0,05193 > 
|
|x3 - x2| =|1,33676 – 1,36921| = 0,03245 > 
| ,
,
|
,
 Novo Intervalo: x2 = 1,36921 e x3 = 1,33676

117. Método da Secante – Execução Algoritmo
ç
g

Exemplo: Considere-se a função f(x) = x3 - x - 1,
 = 0,003, x0 = 1,5 e x1 = 1,7:
Cálculo da 3ª aproximação x2 = 1,36921 e x3 = 1,33676
f(x2) = 0,19769 > 0
f(x3) = 0,05193 > 0
x4 = [1,36921 x (0,05193) - 1,33676 x (0,19769)] =
[(0,05193) - 0,19769]
x4 = 1,3252
 Teste de Parada

|f(x4)| = |0,00206| = 0,00206 <   cond. atendida
|x4 – x3| =|1,3252 – 1,33676| = 0,01156 > 

118. Método da Secante

Vantagens


Cálculos mais convenientes que do método de Newton


Rapidez processo de convergência
Desempenho elevado
Desvantagens
Se o cálculo f’(x) não for difícil, então o método logo será
( )
g
substituído pelo de Newton-Raphson
 Se o gráfico da função for paralela a um dos eixos e/ou
tangencia o eixo das abscissas em um ou mais pontos,
logo não se deve usar o Método da Secante


119. Zeros Reais de Funções
Reais – Comparação entre os
métodos
Prof. Wellington Passos de Paula
wpassos@ufsj.edu.br

120. Comparação entre os métodos
p
ç

Critérios de Comparação

Garantias de Convergência

Rapidez de Convergência

Esforço Computacional

Critério de Parada

121. Comparação entre os métodos
p
ç

Garantias de Convergência

Bisseção e Posição Falsa

Convergência garantida, desde que a função seja contínua
num intervalo [a,b] , tal que f(a)f(b) < 0

Ponto Fixo, Newton-Raphson e Secante

Condições mais restritivas de convergência

Se as condições de convergência forem satisfeitas, os dois
últimos métodos são mais rápidos do que os demais
estudados

122. Comparação entre os métodos
p
ç

Rapidez de Convergência

Número de Iterações  Medida usualmente adotada
para a determinação da rapidez de convergência de um
método

Não deve ser uma medida conclusiva sobre o tempo de
execução do programa

Tempo gasto na execução de uma iteração  Variável
de método para método

123. Comparação entre os métodos
p
ç

Esforço Computacional

Indicadores

Número de operações efetuadas a cada iteração

Complexidade das operações

Número de decisões lógicas

Número de avaliações de função a cada iteração

124. Comparação entre os métodos
p
ç

Esforço Computacional

Conclusões gerais sobre a eficiência computacional de
um método.

Bisseção  Cálculos mais simples por iteração

Newton  Cálculos mais elaborados

Número de iterações da Bisseção é, na grande maioria
das vezes, muito maior do que o número de iterações
efetuadas por Newton

125. Comparação entre os métodos
p
ç

Critério de Parada

Se o objetivo for a redução do intervalo que contém a
raiz  Bisseção (não usar o Método da Posição Falsa)

Se a escolha parte de um valor inicial para a raiz 
Newton-Raphson ou da Secante (pois trabalham com
aproximações xk para a raiz exata)

126. Comparação entre os métodos
p
ç

Conclusão:

Condições a Serem Satisfeitas pelo Método Ideal

Convergência assegurada

Ordem de convergência alta

Cálculos por iteração simples

Atender aos objetivos quanto ao critério de parada

Não existe método perfeito para todos os casos

A escolha está diretamente relacionada com a equação
cuja solução é desejada

Critérios vistos anteriormente

Comportamento da função na região da raiz exata, etc

127. Comparação entre os métodos
p
ç

Conclusão:

Exemplo:

Caso seja fácil a verificação das condições de
convergência e o cálculo de f’(x)  Newton-Raphson

Caso seja trabalhoso obter e/ou avaliar f’(x), uma vez que
não é necessária a obtenção de f’(x)  Secante

Todavia, mesmo os métodos acima possuem restrições:

Tendência da curva ao paralelismo a qualquer um dos eixos
 dificulta o uso do Método de Newton ( f’(x)  0 )

Tendência da função à tangência ao eixo das abscissas em
um ou mais pontos  difi lt o uso d Mét d d S
i
t
dificulta
do Método da Secante
t
( f (xk-1) ≈ f (xk) )

128. Comparação entre os métodos
p
ç

Exemplo: f(x) = x3 – x – 1
y
4
3
2
1
-4
4
-3
3
-2
2
-1
1
0
1
2
3
4
5
x
-1
-2
-3
-4
  [1, 2 ],  = 10 -6

129. Comparação entre os métodos
p
ç

Exemplo: f(x) = x3 – x – 1
Observações:

Melhor desempenho: Método do Ponto Fixo

Métodos de Newton e Secante: muitas iterações pois
houve divergência no inicio da execução
( denominador  0 )

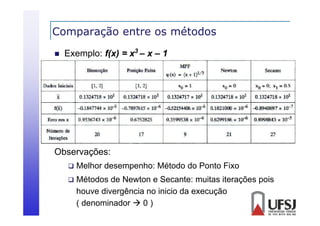
130. Comparação entre os métodos
p
ç

Exemplo: f(x) = 4 sen(x) – e2   [0, 1 ],  = 10 -5
Observações:

Melhor desempenho: Método de Newton, devido à boa
escolha de x0

131. Exercícios
f ( x)  x 2  x  6, encontre
1) A partir do gráfico da função
a raiz   [1, 3] , d d a tolerância   10 4 .
i
dada
l â i
Utilize x0  1,5 e x1  1,7.
y
4
Resposta: 3 iterações
para cada método.
3
f(x)
2
1
-4
-3
-2
-1
0
-1
-2
-3
-4
4
-5
-6
1
2
3
4
5
x