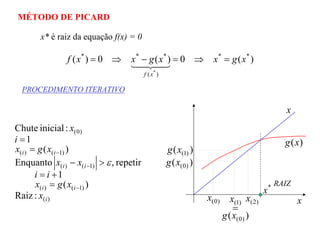
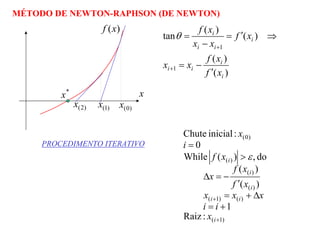
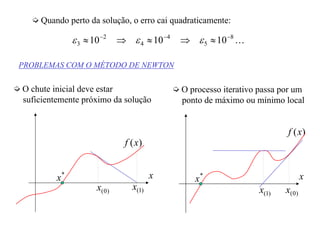
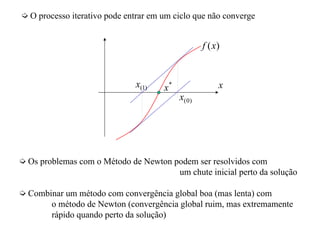
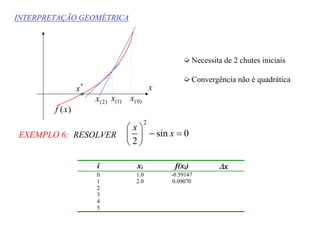
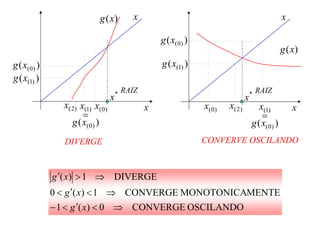
1) O documento discute métodos para calcular raízes de equações, que são necessários para resolver problemas de engenharia. 2) Os métodos incluem o método de Picard, método de Newton-Raphson, método da bisseção e método da secante, que usam procedimentos iterativos para aproximar as raízes. 3) Cada método tem suas vantagens e desvantagens em termos de convergência e facilidade de implementação.

1. CÁLCULO DE RAIZ DE EQUAÇÃOCÁLCULO DE RAIZ DE EQUAÇÃO
Necessidade de determinar a raiz de uma equação
em diversos problemas de engenharia, isto é, determinar x, tal que:
0)( =xf
Algumas equações mais simples possuem solução analítica, como
3e2065
10202
2
==⇒=+−
−=⇒−=
xxxx
xx
Na maioria dos casos (equação não-linear), as raizes da equação
não podem ser determinadas analiticamente
Deve-se utilizar procedimentos iterativos para determinar a(s) raiz(es)

2. MÉTODO DE PICARD
)(0)(0)( **
)(
***
*
xgxxgxxf
xf
=⇒=−⇒=
43421
x* é raiz da equação f(x) = 0
PROCEDIMENTO ITERATIVO
)(
)1()(
)1()(
)1()(
)0(
:Raiz
)(
1
repetir,Enquanto
)(
1
:inicialChute
i
ii
ii
ii
x
xgx
ii
xx
xgx
i
x
−
−
−
=
+=
>−
=
=
ε
x
)(xg
x
*
x
RAIZ
)0(x
)( )0(
)1(
xg
x
=
)2(x
)( )0(xg
)( )1(xg

3. 0=− −x
ex
xx
exgex −−
=⇒= )(
EXEMPLO 1: RESOLVER
M
69220.0)(
36788.0)(
1
36788.0
)1()2(
1
)0()1(
)0(
===
===
=
−
−
exgx
exgx
x
n xn g(xn)
0 1 0.36788
1 0.36788 0.69220
2 0.69220 0.50047
3 0.50047 0.60624
4 0.60624 0.54540
5 0.54540 0.57961
6 0.57961 0.56012
7 0.56012 0.57114
8 0.57114 0.56488
9 0.56488 0.56843
10 0.56843 0.56641
11 0.56641 0.56756
. . .
20 0.56714 0.56714
01=−x
12)(12 −=⇒−= xxgxx
EXEMPLO 2: RESOLVER
M
6.018.02)(
8.019.02)(
9.0
)1()2(
)0()1(
)0(
=−×==
=−×==
=
xgx
xgx
x
n x n g ( x n )
0 0 . 9 0 . 8
1 0 . 8 0 . 6
2 0 . 6 0 . 2
3 0 . 2 - 0 . 6
Processo iterativo diverge
PORQUE ???

4. x)(xg
x
*
x
RAIZ
)0(x
)( )0(
)1(
xg
x
=
)2(x
)( )0(xg
)( )1(xg
DIVERGE
x
)(xg
x
*
x
RAIZ
)0(x
)( )0(
)1(
xg
x
=
)2(x
)( )0(xg
)( )1(xg
CONVERVE OSCILANDO
OSCILANDOCONVERGE0)(1
MENTEMONOTONICACONVERGE1)(0
DIVERGE1)(
⇒<′<−
⇒<′<
⇒>′
xg
xg
xg

5. MÉTODO DE BISSEÇÃO
SE f(x) É UMA FUNÇÃO CONTÍNUA E f(a).f(b) < 0
A RAIZ DE f(x) PERTENCE AO INTERVALO (a,b)
MÉTODO DE BISSEÇÃO CRIA UMA SEQUENCIA DE INTERVALOS
CADE VEZ MENOR QUE CONTENHA A RAIZ
)(xf
x
*
x
0a
0b
),( 00 ba
),( 11 ba
1m 2m
( )
( )
i
iii
ii
ii
ii
ii
ii
ii
i
i
m
bam
ii
mb
aa
mfaf
bb
ma
bfmf
mf
bam
i
bfafba
:Raiz
21
1
end
then0)()(if
end
then0)()(if
do,)(While
21
1
0)()(quetaleEscolher
11
1
1
1
1
00
0000
−−
−
−
−
−
+=
+=
=
=
<⋅
=
=
<⋅
>
+=
=
<⋅
ε

6. 0sin
2
2
=−





x
x
EXEMPLO 3: RESOLVER
i ai-1 f(ai-1) bi-1 f(bi-1) mi f(mi)
1 1.5 <0 2 >0 1.75 <0
2 1.75 2 1.875 <0
3 1.875 2 1.9375 >0
4 1.875 1.9375 1.90625 <0
5 1.90625 1.9375 1.9219
CONVERGÊNCIA EXTREMAMENTE LENTA
CONVERGÊNCIA MELHORA USANDO VALORES DE f(x)
NO CÁLCULO DE mi
)()(
)()(
11
1111
−−
−−−−
+
+
=
ii
iiii
i
bfaf
bfaafb
m

7. MÉTODO DE NEWTON-RAPHSON (DE NEWTON)
)(xf
x*
x
)0(x)1(x)2(x
)(
)(
)(
)(
tan
1
1
i
i
ii
i
ii
i
xf
xf
xx
xf
xx
xf
′
−=
⇒′=
−
=
+
+
θ
PROCEDIMENTO ITERATIVO
)1(
)()1(
)(
)(
)(
)0(
:Raiz
1
)(
)(
do,)(While
0
:inicialChute
+
+
+=
∆+=
′
−=∆
>
=
i
ii
i
i
i
x
ii
xxx
xf
xf
x
xf
i
x
ε

8. 0sin
2
2
=−





x
x
EXEMPLO 4: RESOLVER
i xi f(xi) f’(bi) ∆x
0 1.5 0.434995 -0.67926 0.64039
1 2.14039 -0.30319 -1.60948 -0.18838
2 1.95201 -0.02437 -1.34805 -0.01808
3 1.93393 -0.00023 -1.32217 -0.00018
4 1.93375 0.000005 -1.32191
CONVERGÊNCIA RÁPIDA
O TAMANHO DO PASSO DIMINUI A CADA ITERAÇÃO
DE UM FATOR DE 10

9. 0=− −x
exEXEMPLO 5: RESOLVER
i xi f(xi) f’(bi) ∆x
0 0.0
1
2
3
4

10. PROPRIEDADE DE CONVERGÊNCIA
Vamos supor que α é uma raiz simples de f(x): 0)(e0)( ≠′= αα ff
Obter uma estimativa de erro para a aproximação xn do Método de Newton
αε −= nn x
Expandindo f(x) em série de Taylor em x=xn com um passo α- xn
( )
)(
)(
2
1
lim
)(
)(
2
1
)(
)()(
2
1
)(
)(
)(
)()(
2
1
)(
)(
)(
),();()(
2
1
)()()(0
0)()(
2
2
12
1
2
1
2
2
1
α
α
ε
ε
εξ
εε
ξα
εα
ξα
α
αξξαα
αα
α f
f
xf
f
xf
fx
xf
xf
x
xf
fx
x
xf
xf
xfxxfxxf
fxxf
n
n
n
x
n
nn
n
n
n
x
n
n
n
n
n
n
n
n
nnnnn
nn
n
n
′
′′
=⇒
′
′′
=
′
′′−
−=−=





′
−−⇒
′
′′−
−=−+
′
⇒
∈′′−+′−+=
⇒==−+
+
→
+
+
+
44 344 21
)(
)(
2
1
α
α
f
f
′
′′

11. Quando perto da solução, o erro cai quadraticamente:
K8
5
4
4
2
3 101010 −−−
≈⇒≈⇒≈ εεε
PROBLEMAS COM O MÉTODO DE NEWTON
O chute inicial deve estar
suficientemente próximo da solução
)(xf
x*
x
)0(x )1(x
)(xf
x
)0(x)1(x
O processo iterativo passa por um
ponto de máximo ou mínimo local
*
x

12. O processo iterativo pode entrar em um ciclo que não converge
)(xf
x*
x
)0(x
)1(x
Os problemas com o Método de Newton podem ser resolvidos com
um chute inicial perto da solução
Combinar um método com convergência global boa (mas lenta) com
o método de Newton (convergência global ruim, mas extremamente
rápido quando perto da solução)

13. MÉTODO DA SECANTE
O cálculo da derivada f’(x) pode ser
muito complicado ou caro computacionalmente
Aproximar a derivada por:
1
1)()(
)(
−
−
−
−
≈′
ii
ii
xx
xfxf
xf
PROCEDIMENTO ITERATIVO
)1(
)()1(
)1()(
)1()(
)(
)(
)1()0(
:Raiz
1
)()(
)(
do,)(While
1
e:inicialChute
+
+
−
−
+=
∆+=
−
−
−=∆
>
=
i
ii
ii
ii
i
i
x
ii
xxx
xfxf
xx
xfx
xf
i
xx
ε

14. INTERPRETAÇÃO GEOMÉTRICA
)(xf
x*
x
)0(x)1(x)2(x
Necessita de 2 chutes iniciais
Convergência não é quadrática
0sin
2
2
=−





x
x
EXEMPLO 6: RESOLVER
i xi f(xi) ∆x
0 1.0 -0.59147
1 2.0 0.09070
2
3
4
5