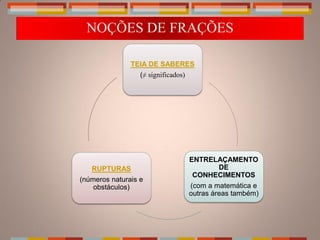
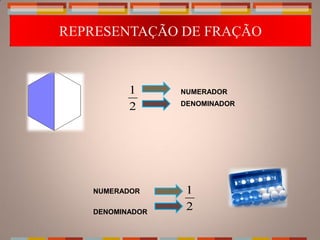
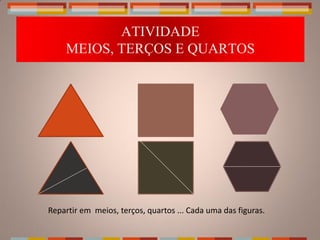
O documento discute o ensino de frações no Ensino Fundamental, abordando conceitos-chave, atividades práticas e o uso de materiais manipuláveis. É destacada a importância das frações para o desenvolvimento intelectual das crianças e como base para operações algébricas. Uma série de atividades são propostas, como uso de discos, jogos e resolução de problemas, para explorar representações e comparações de frações.

1. F
R
A
Ç
Ã
O

2. ESTADO DE MATO GROSSO
SECRETARIA DE ESTADO DE EDUCAÇÃO
ASSESSORIA PEDAGÓGICA DE PONTES E LACERDA
CENTRO DE FORMAÇÃO DOS PROFISSIONAIS DA
EDUCAÇÃO BÁSICA
PROFESSORAS: ROSANGELA VANDERLEI DA SILVA CUBA
E
RUTH MENDES DE SOUZA SANTOS
ESCOLA ESTADUAL DEPUTADO DORMEVIL FARIA

3. QUESTÕES GERADORAS
Você costuma repartir?
O quê?
Como?
Com quem?
Você já ouviu a palavra fração?
Onde?
Em qual situação?

4. FRAÇÕES EM NOSSA VIDA

5. FRAÇÕES EM NOSSA VIDA

6. QUESTÕES GERADORAS
Segundo os PCN´s o ensino de frações é iniciado no segundo ciclo
do Ensino Fundamental (4ª e 5ª anos) e concluído no terceiro
ciclo (6ª e 7ª anos). Em Mato Grosso as turmas correspondentes
seriam das do 2º Ciclo e a 1ª Fase do 3º Ciclo.
RELEVÂNCIA DO ESTUDO DAS FRAÇÕES
o estudo do conceito de fração aperfeiçoa a habilidade de
PRÁTICO dividir, o que permite entender e manipular melhor os
problemas do mundo real.
as frações proporcionam um rico campo, dentro do qual as
crianças podem desenvolver e expandir suas estruturas mentais
PSICOLÓGICA para um desenvolvimento intelectual contínuo, principalmente
pelo fato de serem explorados no período que corresponde à
transição do período concreto para o operatório formal.
a compreensão do número racional fornece a base sobre
MATEMÁTICO a qual serão construídas, mais tarde, as operações
algébricas elementares.
Behr e colaboradores (1983)

7. FRAÇÃO NO 1º CICLO
O QUE E COMO TRABALHAR ?
Este conteúdo deve ser trabalhado
apenas noções de frações, a idéia de
metades, a comparação entre as partes. As
frações devem ser introduzidas como
repartir em partes iguais (divisão). Fazendo
uso de materiais manipuláveis.
(Nunes, Bryant)
Trabalhar as frações:
1 1 1 1
2 3 4 6

8. UM POUCO DE HISTÓRIA
Segundo Caraça (1952), os números
racionais surgiram como necessidade
humana, a partir do momento em
que o ato de contar, típico das
grandezas discretas, não foi mais
suficiente para quantificar grandezas
contínuas, como porções de terra,
por exemplo. A tentativa de resolver
esse problema resultou numa forma
mais sofisticada de contar, em que
não se contavam objetos, mas se
estabelecia um padrão de
comparação e se contava o número
de vezes que o objeto era maior que
esse padrão.

9. MAIS HISTÓRIA...
Dessa necessidade, fortemente associada ao que hoje
denominamos “medir”, surgiu o número racional. O ato de
medir se fundamenta na fixação do referencial, que adquire o
status de unidade quando o estudante conquista a capacidade
de generalizar, caminhando, da idéia de fração –
aparentemente simples – para idéia de número racional,
passando das associações aos objetos físicos às abstrações
características dos objetos matemáticos.

10. NOÇÕES DE FRAÇÕES
TEIA DE SABERES
(≠ significados)
ENTRELAÇAMENTO
RUPTURAS DE
CONHECIMENTOS
(números naturais e
obstáculos) (com a matemática e
outras áreas também)

11. ATIVIDADE
LEITURA DO LIVRO

12. ATIVIDADE
DO LIVRO
Caixa Mural

13. COMPREENDENDO...
 O que a mamãe pata quis dizer com: divida ao meio
sem truque algum?
 Como a mamãe pata mandou que DINO dividisse o
pirulito na primeira vez? Mostre no pirulito como ficou.
 Apresente a representação da parte do pirulito que
cada um receberia, antes do pato ZINHO chegar.
 Em sua opinião, qual patinho teve melhor atitude?
Por que?
 Se você participasse da história, no lugar do pato
XATO, como você procederia.

14. Questionamentos que podem ser feitos aos alunos
Você já repartiu alguma coisa com seus
coleguinhas?
Explique como você fez para repartir em partes
iguais?
O que você pensa sobre a atitude do pato Dino
ao dar o palito ao irmão Lino?
O que você pensa sobre a atitude do pato Xato
ao dizer “Em meu terço ninguém mais toca”?
O que você percebeu na relação entre o pato
Lino e o pato Zinho?

15. PROFESSOR, VAMOS RECORDAR?
O QUE É FRAÇÃO ?
1 NUMERADOR = Indica o número de partes
tomadas
2 DENOMINADOR = N.º de partes em que a
unidade está dividida

16. CONTINUANDO...
REPRESENTAÇÃO DE FRAÇÃO
1 NUMERADOR
DENOMINADOR
2
NUMERADOR 1
DENOMINADOR
2

17. D
I
S
C
O
D
E
F
R
A
Ç
Õ
E
S

19. ATIVIDADE
DISCOS DE FRAÇÕES
Objetivos:
Identificar a fração inteira e as partes (metade,
terços, quartos e sextos);
trabalhar equivalência das frações a partir da
sobreposição das peças;
comparar frações, estabelecendo um diálogo
sem a necessidade de qualquer formalização
(quem é maior que..., igual a...);
compreender a relação entre o número de
cortes e o tamanho da parte.

20.  Mostre o disco inteiro.
 Ele foi repartido em diferentes pedaços?
 Em quantos?
 Os pedaços são iguais?
 Observe o tamanho do pedaços e a
quantidade de pedaços. Que relação você
percebe.
ISSO CHAMAMOS DE FRAÇÃO.

21.  Tem algum disco que não foi repartido? Que disco
representar o todo? Que fração escrevo para representar
o todo?
 Tem algum disco que foi repartido em dois partes? Que
pedaço representa a metade do disco? Que fração
escrevo para representar a metade?
 Tem algum disco que foi repartido em três partes? Que
pedaço representa a terça parte do disco? Que fração
escrevo para representar a terça parte?
 Tem algum disco que foi repartido em quatro partes? Que
pedaço representa a quarta parte do disco? Que fração
escrevo para representar a quarta parte?

22.  Se eu pegar dois pedaços que representam a quarta parte,
que pedaço eu tenho? Qual a fração? Posso trocar por
outro de mesmo tamanho?
 Tem algum disco que foi repartido em seis partes? Que
pedaço representa a sexta parte do disco? Que fração
escrevo para representar a sexta parte?
 Se eu pegar dois pedaços que representam a sexta parte,
que pedaço eu tenho? Qual a fração? Posso trocar por
outro de mesmo tamanho?
 Se eu pegar três pedaços que representam a sexta parte,
que pedaço eu tenho? Qual a fração? Posso trocar por
outro de mesmo tamanho?

23. C
O
I
M
N
P
T
L
E
E
I
T
R
E
O
O

24. ATIVIDADE
COMPLETE O INTEIRO
Objetivo:
Estabelecer relação entre as partes e o inteiro
fazendo comparações entre elas.
Usando o dado , o molde e três discos da atividade
acima:
 Cada lado do molde representa um disco que não
foi repartido, o inteiro 1 .
1
 um disco dividido em duas partes iguais ;
2
 outro dividido em três partes iguais 1 ;
3
1
 e o disco restante dividido em seis partes iguais 6

25. Regras:
Usando o molde como padrão para a unidade,
joga-se o dado e pega-se a peça
correspondente à fração que caiu para cima e
coloca dentro do molde, repete o procedimento
sucessivamente até completar o inteiro. O
aluno passa a vez quando a fração sorteada
não corresponder ao que falta para completar o
inteiro.

26. ATIVIDADE
ASSISTIR AO VÍDEO
Objetivos:
•Apresentar situação real em que o uso das
frações se torna necessário;
•Identificar as frações ½, 1/3, e 1/9 perceber que a
soma delas não formam o inteiro;
O HOMEM QUE CALCULAVA
e ...
Vamos entender o que aconteceu...
(utilize dos discos para representar a situação
apresentada)

27. ATIVIDADE
PAPA TODAS
Objetivos:
compreender o conceito de fração;
comparar frações com diferentes
denominadores;
noção de equivalência de frações;
leitura e representação de frações;
resolução de problemas que envolvam frações
e realizar cálculo mental com frações.

28. ATIVIDADE
PAPA TODAS
Regras:
O jogo é para grupos de 4 a 5 alunos (não
sugerimos duplas porque ele perde o sentido de
desafio)
Todas as cartas do baralho são distribuídas
entre os jogadores que não vêem suas cartas.
Cada jogador coloca suas cartas em uma pilha
com os números virados para baixo.
A tabela com as tiras de fração é colocada no
centro da mesa de modo que todos a vejam.

29. ATIVIDADE
PAPA TODAS
Os jogadores combinam entre si um sinal ou
uma palavra. Dado o sinal todos os jogadores
viram a carta de cima de sua pilha ao mesmo
tempo e comparam as frações. O jogador que
tiver a carta representando a maior fração vence
a rodada e fica com todas as cartas (Papa
todas)
A tabela de tiras de frações pode ser usada se
necessário para que as comparações sejam
feitas.

30. ATIVIDADE
PAPA TODAS
Se houver duas cartas de mesmo valor todas
as cartas ficam na mesa e na próxima rodada
o jogador com a maior carta papa todas,
inclusive aquelas que estão na mesa.
O jogo termina quando as cartas acabarem.
Jogo Papa todas

31. CONTINUANDO...
ATIVIDADE
DOMINÓ
Vamos jogar dominó relacionando as
representações fracionárias e seu registro
numérico.
Usar as regras do dominó normal.
Jogar em duplas.

32. ATIVIDADE
MEIOS, TERÇOS E QUARTOS
Repartir em meios, terços, quartos ... Cada uma das figuras.

33. 01 - Um relógio circular está marcando
6 horas, que fração do inteiro representa
este?
02 - A formiga está colocando placas no
caminho que vai de sua casa até a casa do
namorado. As placas devem dizer que fração do
caminho ela já percorreu, quando vai visitar o
namorado. Coloque as placas os pontos A, B e
C.

34. 03 - Num estacionamento tem 30 carros,
sendo que ½ deles são da cor branca.
Quantos carros são brancos?
04 - Divida igualmente 5 bolos entre 15
pessoas. Que pedaço cada um receberá?
05 - Para cada vaga no curso de informática
existem 5 candidatos. Qual a fração que
representa a concorrência?

35. 06 - Quantos ovos correspondem a ¼ de
uma dúzia de ovos?
07 - Duas barras de chocolates devem ser
divididas entre 5 crianças. Qual a fração a
ser representada?

36. 08 - Comprei um metro de fita. Dividi a fita em
10 partes iguais. Se cortar onde mostra a
figura, que fração representará cada um dos
pedaços?

37. 09 – Escrevam as frações que representam os
números correspondentes aos pontos
indicados pelas letras A, B e C.

38. SUGESTÕES DE SITE DE LEITURA E
JOGOS
http://escolovar.org/mat_fraccao_jogos.tot.htm
http://www.oswego.org/ocsd-
web/games/fractionflags/fractionflags.html
http://www.facitec.br/revistamat/download/paradidatico
s/guru_completo.pdf

39. REFERÊNCIA BIBLIOGRÁFICA
BITTAR, Marilena. Fundamentos e Metodologias de Matemática para os Ciclos Iniciais do
Ensino Fundamental. Campo Grande.Ed. UFMS, 2ªed. 2005.
BRASIL, Ministério da Educação e do Desporto, Secretaria de Educação Fundamental. Gestar I.
Brasília: MEC/SEF, 2007
BRASIL, Ministério da Educação e do Desporto, Secretaria de Educação Fundamental.
Parâmetros Curriculares Nacionais: Matemática. 3ª ed. Brasília: MEC/SEF, 1998
BRASIL, Ministério da Educação, Secretaria de Educação Básica. Guia do Livro Didático PNLD
2010: Matemática. Brasília: MEC, 2009.
BRIZUELA. Bárbara M. Desenvolvimento Matemático na Criança – Explorando Notações.
Porto Alegre. Ed. Artmed. 2006.
CAMPOS, Tânia Maria Mendonça; RODRIGUES, Wilson Roberto. A Idéia de Unidade na
Construção do Conceito do Número Racional. REVEMAT - Revista Eletrônica de Educação
Matemática. V 2.4, p.68-93, UFSC: 2007.
MACHADO, Nilson José. O Pirulito do Pato. São Paulo: Scipione, 1996.
MATO GROSSO, Secretaria de Estado de Educação. Orientações Curriculares de Mato Grosso.
Cuiabá: SEDUC, 2010. Disponível em
http://www.seduc.mt.gov.br/conteudo.php?sid=463&parent=9909 acessado em 30/11/2011.
NUNES, Terezinha. BRYANT, Peter. Criança fazendo matemática. Porto Alegre, Ed.
Artmed, 1997.
PANIZZA, Mabel. Ensinar Matemática na Educação Infantil e nas Séries Iniciais: Análise e
Proposta. São Paulo ,Ed. Artmed, 2006.
REIS, Silva M. G. A matemática no cotidiano infantil. São Paulo. Ed. Papirus. 2006.
Tahan, Malba. O homem que calculava. São Paulo: Record, 2000.
Site do filme do problema dos camelos de Malba Tahan http://www.youtube.com/watch?v=-
tTD8XU2s2I

40. Mensagem : Você Aprende
Willian Shakespeare

41. O
B
R
I
G
A
D
A
!