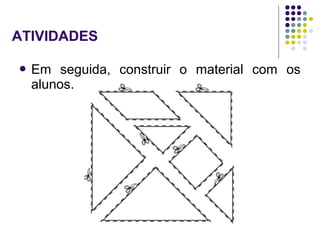
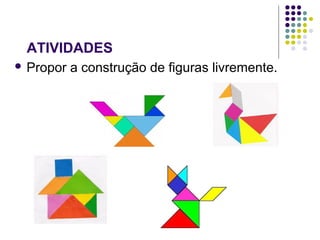
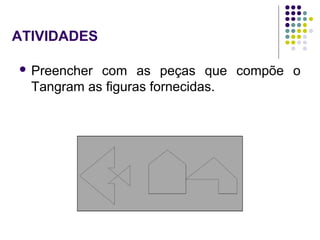
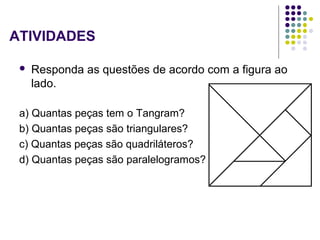
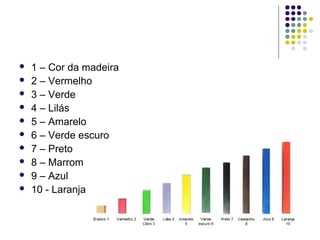
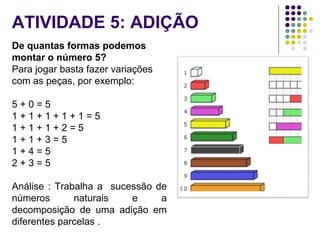
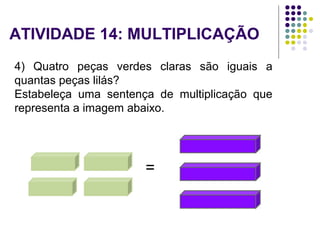
O documento descreve como usar o material Cuisenaire no ensino de matemática, apresentando suas origens, objetivos e várias atividades possíveis com as barras de tamanhos e cores diferentes. As atividades exploram conceitos como adição, subtração, multiplicação e divisão de forma lúdica e manipulativa.