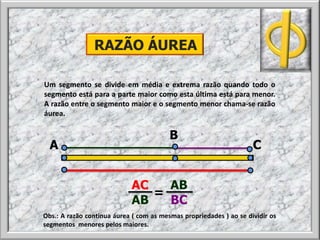
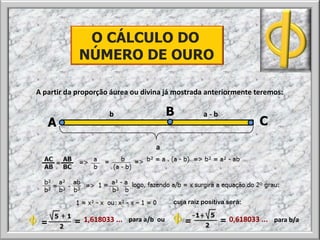
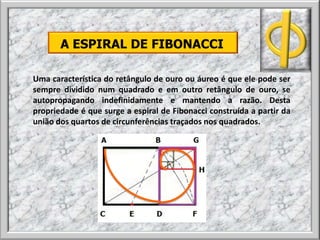
O documento descreve a razão áurea, que é uma proporção encontrada na natureza e na arte que produz harmonia. A razão áurea ocorre quando um segmento é dividido de forma que a parte maior está para o todo assim como o todo está para a parte menor. Isso gera o número de ouro, aproximadamente 1,618. O documento fornece exemplos de onde a razão áurea aparece, como no Partenon e no crescimento de plantas.

1. “O poder da seção áurea em criar harmonia deriva de sua propriedade única
de unir partes diferentes de um todo, de forma a que cada uma delas
preserva sua identidade própria, mas amolda-se a um padrão maior de um
todo.”
György Doczi - O Poder dos Limites

2. Um segmento se divide em média e extrema razão quando todo o
segmento está para a parte maior como esta última está para menor.
A razão entre o segmento maior e o segmento menor chama-se razão
áurea.
RAZÃO ÁUREA
A
B
C
AC AB
AB BC
=
Obs.: A razão continua áurea ( com as mesmas propriedades ) ao se dividir os
segmentos menores pelos maiores.

3. A razão áurea foi denominada como tal pelas propriedades que apresenta –
harmonia, continuidade e beleza. Além de estar presente nas obras
humanas ( artes, construções, etc. ), a razão áurea pode ser encontrada no
mundo natural, através das proporções dos seres humanos e dos padrões de
crescimento de muitas plantas, animais e insetos. Fora do nosso mundo
natural a razão áurea também se manifesta como na relação entre as
estrelas em uma galáxia.
POR QUE RAZÃO ÁUREA?
Razão áurea entre o lado e
a diagonal do pentágono
se autopropagando.
Razão áurea entre segmentos
que formam os lados da estrela
( diagonal do pentágono ).
PENTAGRAMA
Símbolo dos Pitagóricos

4. O resultado da divisão do segmento maior pelo menor na razão áurea
é denominado de número de ouro. Sua representação é feita pela
letra grega phi ( símbolo acima ). O número de ouro, que também é
irracional, pode ser escrito de duas maneiras devido a forma dupla de
se encontrar a razão áurea – segmento maior sobre o menor ou
menor sobre o maior. A mais comum é a do maior sobre o menor, o
que origina um valor maior que um.
NÚMERO DE OURO
1,618033 ... ( mais comum )= =
= = 0,618033 ... ( menos comum )

5. A partir da proporção áurea ou divina já mostrada anteriormente teremos:
O CÁLCULO DO
NÚMERO DE OURO
1,618033 ...= = = = 0,618033 ...
b a - b
a
A C
B
cuja raiz positiva será:
para a/b ou para b/a

6. O RETÂNGULO ÁUREO
A partir de um quadrado ABCD e do ponto médio E de
CD, traça-se um arco de raio EB que intercepta o
prolongamento de CD no ponto F. Completando o
retângulo BDFG com paralelas determina-se as diagonais
dos retângulos ACFG e BDFG que propagarão os
próximos retângulos áureos no sentido anti-horário
como o BGHI.
Ia
ba/2
Um retângulo cuja razão entre a medida do comprimento e a medida
da largura é de aproximadamente 1,618... chama-se retângulo de ouro
ou retângulo áureo.
DEMONSTRAÇÃO:

7. A ESPIRAL DE FIBONACCI
Uma característica do retângulo de ouro ou áureo é que ele pode ser
sempre dividido num quadrado e em outro retângulo de ouro, se
autopropagando indefinidamente e mantendo a razão. Desta
propriedade é que surge a espiral de Fibonacci construída a partir da
união dos quartos de circunferências traçados nos quadrados.

8. A ESPIRAL DE FIBONACCI
Originalmente a espiral de Fibonacci é traçada a partir da sequência
de números (0,1,1,2,3,5,8,13,21, ... ) onde cada termo a partir do
terceiro é igual à soma dos dois anteriores. Nesta sequência, quando
se divide o posterior pelo anterior, a partir do terceiro termo, os
resultados vão se aproximar do número de 1,618 ... ou, dividindo
anterior pelo posterior, do número 0,618 ... que representam a razão
áurea.
Leonardo Fibonacci, também
conhecido como Leonardo de Pisa
( 1170 - 1250), foi um talentoso
matemático italiano que ficou
conhecido pela sequência que
leva seu nome e pela introdução
dos algarismos arábicos na
Europa.
Novo quadrado

9. EXEMPLOS DE ONDE APARECE
A RAZÃO ÁUREA
1. Na pirâmide de Quéops em Gisé, Egito, quando se divide a altura
de uma face e a metade do lado da base da grande pirâmide;
2. O Partenon, em Atenas, Grécia, se encaixa perfeitamente no
retângulo áureo;
3. No aumento do diâmetro das espirais das sementes de um
girassol;
4. Na diminuição das folhas de uma árvore à medida que se sobe
de altura;
5. Na relação entre estrelas de uma galáxia;
6. No estudo do comportamento da luz e dos átomos.

10. FONTES
1. Oliveira, Edson de; Ferreira, Thiago Emanoel. O número de ouro e suas manifestações na
natureza e na arte. Revista Complexus – Instituto Superior de Engenharia Arquitetura e
Design – CEUNSP, Salto, ano. 1, nº2, setembro de 2010.
http://engenho.info/revista/ed02/dartigos/5-Artigop64-81.pdf. Acesso em 29 de agosto de
2013.
2. Carvalho, Jurandir Jacques de. Razão Áurea. Belo Horizonte: Universidade Federal de
Minas Gerais, 2008. Trabalho de conclusão de curso de especialização.
http://www.mat.ufmg.br/~espec/monografiasPdf/Monografia_Jurandir.pdf. Acesso em 29
de agosto de 2013.
3. LÍVIO, Mario. Razão Áurea: A história de Fi, um número surpreendente. Rio de Janeiro:
Record, 2008.
4. Queiroz, Rosania Maria. Razão Áurea: A beleza de uma razão surpreendente. Londrina:
Universidade Estadual de Londrina, 2008. Artigo Final apresentado ao Programa de
Desenvolvimento Educacional.
http://www.diaadiaeducacao.pr.gov.br/portals/pde/arquivos/674-4.pdf . Acesso em 30 de
agosto de 2013.

11. O blog aborda assuntos de Matemática, Astronomia, Natureza, Humor,
História e Esportes, além de trabalhos e projetos realizados nas escolas em
que atuei e atuo. É mais um canal aberto de comunicação com os alunos e
demais visitantes que queiram se inteirar de outras experiências realizadas em
escolas públicas.
Prof. Jonas
PEDRO VELHO/RN/BR
SETEMBRO DE 2013
SLIDES PRODUZIDOS PARA O BLOG:
jfgf2011.blogspot.com