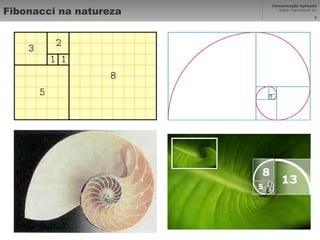
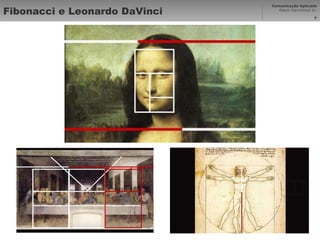
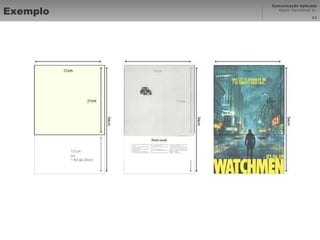
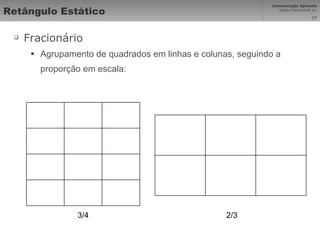
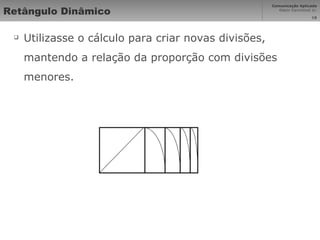
O documento descreve o princípio da proporção áurea, identificada observando padrões na natureza e usada na diagramação. A proporção segue a série de Fibonacci e foi estudada por Leonardo da Vinci e Luca Pacioli em 1509. Sua aplicação na arte, arquitetura e design busca dividir espaços de forma harmoniosa seguindo a escala de 1,618.

1. Proporção Áurea Utilizando o Princípio de Vitruvio na diagramação

2. O princípio de Vitruvio “ Para que um todo, dividido em partes desiguais, pareçam harmonioso, é preciso que exista, entre a parte pequena e a maior, a mesma relação que entre a grande e o todo” . (Euclides) A natureza humana interpreta ser mais agradável formas que não sejam matematicamente determinadas (exatas). A natureza não é ordenada e nem padronizada matematicamente. O caos é mais natural do que modelos exatos.

3. Origem Em 1509, o matemático Luca Pacioli e Leonardo DaVinci publicaram o livro “Divina Proportione”. O estudo descobriu que as coisas na natureza evoluem exponencialmente, seguindo uma proporção perfeita. Essa proporção foi identificada observando e medindo a natureza do crescimento, com base no cálculo dos números de Fibonacci.

4. Série de Fibonacci A proporção perfeita segue uma escala de crescimento, em que cada número é a soma dos dois anteriores: 0:1:1:2:3:5:8:13:21:34:55:89:144:233:377 Após muitos cálculos, foi identificado que a proporção cresce na escala 1.618033989. Para simplificar: Phi = 1.618 Na mídia impressa, é comum arredondar para 1.62

5. Fibonacci na natureza

6. Fibonacci e Leonardo DaVinci

7. Fibonacci e Piet Mondrian Composition A 1920 Composition with large blue plane, red back, yellow and gray 1921

8. Fibonacci na arquitetura

9. Fibonacci na mídia

10. Outros nomes Princípio de Vitruvio Proporção Divina Proporção áurea Proporção de ouro Proporção em extrema razão Número Divino Número áureo Número de ouro Regra de Ouro Retângulo Áureo Retângulo de Ouro Seção áurea Razão áurea Razão de ouro Razão de Phidias Divisão de extrema razão Áurea excelência

11. Retângulo áureo A regra universal para regular a proporção é partindo da escala 1:1, que na geometria, pode ser traduzida em um polígono com lados iguais. Por isso a forma mais fácil de calcular a proporção é partindo de um retângulo.

12. Cálculo simples Adicionando um complemento Digamos que está diagramando uma página em uma área viva de 15cm x 24cm. Utilizaremos um quadrado imaginário de 15cm x 15cm. Para achar a proporção correta, calcula 15 x 1,62 = 24,3. 15cm 15cm

13. Exemplo

14. Cálculo simples Dividindo a área Digamos que a altura máxima não pode passar de 24cm. Para achar a proporção correta, calcula 24 x 0,62 = 14,88.

15. The Golden Ratio Calculator Site que ajuda a calcular a proporção áurea de uma área de forma simples: http://goldenratiocalculator.com/

16. Retângulo Estático Inteiro Agrupamento de quadrados para dividir uma composição sequencial em linha: 1 2 3 ...

17. Retângulo Estático Fracionário Agrupamento de quadrados em linhas e colunas, seguindo a proporção em escala: 3/4 2/3

18. Retângulo Dinâmico Utilizasse o cálculo para criar novas divisões, mantendo a relação da proporção com divisões menores.

19. Referência bibliográfica As informações contidas nessa apresentação foram elaboradas com base na minha experiência profissional que, em algum momento, podem contradizer o que é explicado na teoria. Existem algumas informações que são encontradas na Wikipédia. Porém, como seu conteúdo pode ser alterado por qualquer pessoa, sua credibilidade é questionável. Só utilize informações da Wikipédia se você já conhece o assunto e concorda com as definições. Proporção áurea Wikipédia http://pt.wikipedia.org/wiki/Propor%C3%A7%C3%A3o_%C3%A1urea A fórmula da beleza… LedStyle http://www.tuxresources.org/blog/archives/468 O que é proporção divina? Canha http://espaco.com/design/o-que-e-proporcao-divina/ Design e a Proporção Áurea Tiago Pimentel http://www.designinabox.nu/2009/02/design-e-a-proporcao-aurea/ Piet Mondrian http://www.noitesaopaulo.com.br/mondrian/nsp_piet-mondrian.asp Planejamento Visual Gráfico Milton Ribeiro Editora LGE 2007

20. Proporção Áurea Utilizando o Princípio de Vitruvio na diagramação Odair Cavichioli Júnior www.odaircavichioli.com.br