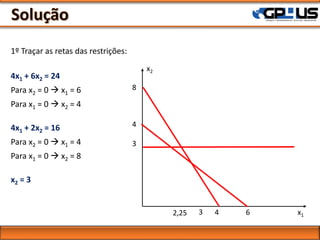
1. O documento apresenta um problema de programação linear com duas variáveis de decisão e descreve como resolver graficamente através de restrições e função objetivo. 2. São mostrados exemplos de representação gráfica de inequações e sistemas com identificação da região de soluções e avaliação da função objetivo. 3. São resolvidos passo a passo problemas propostos utilizando o método gráfico para encontrar a solução ótima.

2. SITE:
• https://www.gp4us.com.br
CONTATO:
• contato@gp4us.com.br

3. Objetivo
Obter a solução de problemas de Programação Linear
através de Modelos Gráficos que obedecem as restrições
impostas pelo Sistema.
Restrição
Um problema de P.L. somente pode ser resolvido
graficamente desde que o modelo em estudo apresente
somente 2 variáveis de decisão.

4. Solução
Qualquer especificação de valores dentro do domínio da
função objetivo.
Solução viável
Uma solução em que todas as restrições são satisfeitas;
Solução ótima
Uma solução que tem o valor mais favorável da função
objetivo;

5. Representação gráfica da inequação: x1 + 2x2 > 10
Para construir a reta correspondente à equação acima, dois pontos
são necessários:
Fazendo x1 = 0 temos 2x2 = 10  x2 = 5
Fazendo x2 = 0 temos x1 = 10
Testando a inequação:
10 + 2 x 5 > 10  20 > 10  Verdadeiro

6. 5
10
(10, 5)
Região de Soluções
x2
x1
x1 + 2x2 > 10
Tudo que esta acima da
reta corresponde a
Região de
Possíveis Soluções

7. Representação gráfica as inequações:
x1 + 3x2 < 12
2x1 + x2 > 16
Fazendo x1 = 0 temos 3x2 = 12  x2 = 4
Fazendo x2 = 0 temos x1 = 12
Fazendo x1 = 0 temos x2 = 16
Fazendo x2 = 0 temos 2x2 = 16  x2 = 8
Restrições de Não Negatividade: x1, x2 > 0

8. x1 + 3x2 < 12
2x1 + x2 > 16
4
12
x2
x1
8
16
12
x1 = 12
x2 = 4
x1 = 8
x2 = 16

9. Avaliar o desempenho da Função Objetivo: Max L = 2x1 + 5x2 na
região de soluções do gráfico abaixo:
6
8
x2
x1
4
8
Max L = 2x1 + 5x2

10. Escolher um valor arbitrário para L, por exemplo: 10
2x1 + 5x2 = 10
2x1 + 5x2 = 15
Fazendo x1 = 0 temos 5x2 = 10  x2 = 2
Fazendo x2 = 0 temos 2x1 = 10  x1 = 5
Fazendo x1 = 0 temos 5x2 = 15  x2 = 3
Fazendo x2 = 0 temos 2x1 = 15  x1 = 7,5
Escolher um outro valor arbitrário para L, por exemplo: 15

11. Max L = 2x1 + 5x2
6
8
x2
x1
4
8
2
3
5 7,5
L = máximoP
Avaliar o desempenho da Função Objetivo: Max L = 2x1 + 5x2 na
região de soluções do gráfico abaixo:

12. 1 – À medida que atribuímos valores a L, obtemos retas paralelas;
2 – À medida que o valor de L aumenta, a reta se afasta da origem do
Sistema de Eixos;
O ponto P do gráfico é a paralela de maior valor dentro da região de
Soluções. Portanto, o ponto P é a solução que maximiza L.
Como P = (0, 6) e L = 2x1 + 5x2, temos que:
L = 2 x 0 + 5 x 6  Lmáximo = 30

16. Resolva o Sistema abaixo através do método gráfico. Max L = {6, 9}
Max L = 3x1 + 3x2
s.a.
2x1 + 4x2 < 12
6x1 + 4x2 < 24
Não Negatividade
x1, x2 > 0

17. 1º Traçar as retas das restrições:
2x1 + 4x2 = 12
Para x2 = 0  x1 = 3
Para x1 = 0  x2 = 3
6x1 + 4x2 = 24
Para x2 = 0  x1 = 4
Para x1 = 0  x2 = 6
6
x2
x1
6
3
4

18. 2º Identificar a Região da Solução:
2x1 + 4x2 < 12
6x1 + 4x2 < 24
6
x2
x1
6
3
4

19. 3º Traçar as retas da F.O. = {3, 6}
3x1 + 3x2 = 3
Para x2 = 0  x1 = 1
Para x1 = 0  x2 = 1
3x1 + 3x2 = 6
Para x2 = 0  x1 = 2
Para x1 = 0  x2 = 2
6
x2
x1
6
3
4
1
1 2
2
L = 3
L = 6

20. 4º Encontrar o Ponto Ótimo.
3x1 + 3x2 = 3
Para x2 = 0  x1 = 1
Para x1 = 0  x2 = 1
3x1 + 3x2 = 6
Para x2 = 0  x1 = 2
Para x1 = 0  x2 = 2
6
x2
x1
6
3
4
1
1 2
2
Ponto Ótimo
Último ponto da Região da
Solução em relação às retas da
Função Objetivo

21. 5º Encontrar os valores de x1 e x2
2x1 + 4x2 = 12
6x1 + 4x2 = 24
x1 + 2x2 = 6
3x1 + 2x2 = 12
x1 = 6 - 2x2
3(6 - 2x2) + 2x2 = 12
18 - 6x2 + 2x2 = 12
- 4x2 = -6
x2 = 1,5
Substituindo:
x1 = 3
Como o Ponto Ótimo é o
encontro das retas, seus valores
podem ser encontrados através
da solução das inequações.
6
x2
x1
6
3
4
1
1 2
2
Ponto Ótimo
/ 2

22. 6º Aplicar os valores de x1 e x2 na F.O.
Max L = 3x1 + 3x2
Max L = ( 3 * 3) + (3 * 1,5) = 13,5

23. Resolva o Sistema abaixo através do método gráfico. C = {18, 12}
Min C = 2x1 + 3x2
s.a.
x1 + x2 > 5
5x1 + x2 > 10
x1 < 8
Não Negatividade
x1, x2 > 0

24. 1º Traçar as retas das restrições:
x1 + x2 = 5
Para x2 = 0  x1 = 5
Para x1 = 0  x2 = 5
5x1 + x2 = 10
Para x2 = 0  x1 = 2
Para x1 = 0  x2 = 10
x1 = 8 5
x2
x1
10
5
2 8

25. 2º Identificar a Região da Solução:
x1 + x2 > 5
5x1 + x2 > 10
x1 < 8
5
x2
x1
10
5
2 8

26. 3º Traçar as retas da F.O. = {18, 12}
2x1 + 3x2 = 18
Para x2 = 0  x1 = 9
Para x1 = 0  x2 = 6
2x1 + 3x2 = 12
Para x2 = 0  x1 = 6
Para x1 = 0  x2 = 4
5
x2
x1
10
5
2 8 9
6
6
4
C = 18
C = 12

27. 4º Encontrar o Ponto Ótimo.
2x1 + 3x2 = 18
Para x2 = 0  x1 = 9
Para x1 = 0  x2 = 6
2x1 + 3x2 = 12
Para x2 = 0  x1 = 6
Para x1 = 0  x2 = 4
Último ponto da Região da
Solução em relação às retas da
Função Objetivo
5
x2
x1
10
5
2 8 9
6
6
4
C = 18
C = 12
Ponto Ótimo

28. 5º Encontrar os valores de x1 e x2
x1 = 5
Como o Ponto
Ótimo encontra-se
no eixo de x1, o valor
de x2
consequentemente
é zero.
x2 = 0
5
x2
x1
10
5
2 8 9
6
6
4
C = 18
C = 12
Ponto Ótimo

29. 6º Aplicar os valores de x1 e x2 na F.O.
Min C = 2x1 + 3x2
Max L = ( 2 * 5) + (3 * 0) = 10

30. Resolva o Sistema abaixo através do método gráfico. L = {24, 30}
ax
Max L = 2x1 + 3x2
s.a.
4x1 + 6x2 < 60
x1 + x2 > 12
Não Negatividade
x1, x2 > 0

31. 1º Traçar as retas das restrições:
4x1 + 6x2 = 60
Para x2 = 0  x1 = 15
Para x1 = 0  x2 = 10
x1 + x2 = 12
Para x2 = 0  x1 = 12
Para x1 = 0  x2 = 12
15
x2
x1
12
10
12

32. 2º Identificar a Região da Solução:
4x1 + 6x2 < 60 – R1
x1 + x2 > 12 – R2
15
x2
x1
12
10
12

33. 3º Traçar as retas da F.O. = {24, 36}
2x1 + 3x2 = 24
Para x2 = 0  x1 = 12
Para x1 = 0  x2 = 8
2x1 + 3x2 = 36
Para x2 = 0  x1 = 18
Para x1 = 0  x2 = 12
15
x2
x1
12
10
12
8
18
C = 36
C = 24

34. 4º Encontrar o Ponto Ótimo.
2x1 + 3x2 = 24
Para x2 = 0  x1 = 12
Para x1 = 0  x2 = 8
2x1 + 3x2 = 36
Para x2 = 0  x1 = 18
Para x1 = 0  x2 = 12
Último ponto da Região da
Solução em relação às retas da
Função Objetivo
15
x2
x1
12
10
12
8
18
C = 36
C = 24
Ponto Ótimo

35. 5º Encontrar os valores de x1 e x2
x1 = 15
Como o Ponto
Ótimo encontra-se
no eixo de x1, o valor
de x2
consequentemente
é zero.
x2 = 0
15
x2
x1
12
10
12
8
18
C = 36
C = 24
Ponto Ótimo

36. 6º Aplicar os valores de x1 e x2 na F.O.
Max L = 2x1 + 3x2
Max L = ( 2 * 15) + (3 * 0) = 15

37. Resolva o Sistema abaixo através do método gráfico. L = {16, 24, 32}
24, 32
Max L = 2x1 + 4x2
s.a.
8x1 + 7x2 < 56
x2 < 5
x1 < 4
Não Negatividade
x1, x2 > 0

38. 1º Traçar as retas das restrições:
8x1 + 7x2 = 56
Para x2 = 0  x1 = 7
Para x1 = 0  x2 = 8
x1 < 4
x2 < 5
7
x2
8
5
4 x1

39. 2º Identificar a Região da Solução:
8x1 + 7x2 < 56
x1 < 4
x2 < 5
7
x2
8
5
4 x1

40. 3º Traçar as retas da F.O. = {16, 24, 32}
2x1 + 4x2 = 16
Para x2 = 0  x1 = 8
Para x1 = 0  x2 = 4
2x1 + 4x2 = 24
Para x2 = 0  x1 = 12
Para x1 = 0  x2 = 6
2x1 + 4x2 = 32
Para x2 = 0  x1 = 16
Para x1 = 0  x2 = 8 7
x2
x1
8
5
4 8 12
4
6
C = 16 C = 24
C = 32

41. 4º Encontrar o Ponto Ótimo.
2x1 + 4x2 = 16
Para x2 = 0  x1 = 8
Para x1 = 0  x2 = 4
2x1 + 4x2 = 24
Para x2 = 0  x1 = 12
Para x1 = 0  x2 = 6
2x1 + 4x2 = 32
Para x2 = 0  x1 = 16
Para x1 = 0  x2 = 8
Último ponto da Região da
Solução em relação às retas da
Função Objetivo
7
x2
x1
8
5
4 8 12
4
6
C = 16 C = 24
C = 32
Ponto Ótimo

42. 5º Encontrar os valores de x1 e x2
x2 = 5
8x1 + 7x2 = 56
8x1 + 7 * 5 = 56
8x1 = 56 – 35
8x1 = 21
x1 = 2,62
7
x2
x1
8
5
4 8 12
4
6
C = 16 C = 24
C = 32
Ponto Ótimo

43. 6º Aplicar os valores de x1 e x2 na F.O.
Max L = 2x1 + 4x2
Max L = ( 2 * 2,62) + (4 * 5) = 25,25

44. Resolva o Sistema abaixo através do método gráfico. L = {180, 240}
Max L = 80x1 + 60x2
s.a.
4x1 + 6x2 < 24
4x1 + 2x2 < 16
x2 < 3
Não Negatividade
x1, x2 > 0

45. 1º Traçar as retas das restrições:
4x1 + 6x2 = 24
Para x2 = 0  x1 = 6
Para x1 = 0  x2 = 4
4x1 + 2x2 = 16
Para x2 = 0  x1 = 4
Para x1 = 0  x2 = 8
x2 = 3
6
x2
4
3
x14
8
2,25 3

46. 2º Identificar a Região da Solução:
4x1 + 6x2 < 24
4x1 + 2x2 < 16
x2 < 3
6
x2
4
3
x14
8
2,25 3

47. 3º Traçar as retas da F.O. = {180, 240}
80x1 + 60x2 = 180
Para x2 = 0  x1 = 2,25
Para x1 = 0  x2 = 3
80x1 + 60x2 = 240
Para x2 = 0  x1 = 3
Para x1 = 0  x2 = 4
6
x2
4
3
x14
8
2,25 3

48. 4º Encontrar o Ponto Ótimo.
2x1 + 4x2 = 16
Para x2 = 0  x1 = 8
Para x1 = 0  x2 = 4
2x1 + 4x2 = 24
Para x2 = 0  x1 = 12
Para x1 = 0  x2 = 6
2x1 + 4x2 = 32
Para x2 = 0  x1 = 16
Para x1 = 0  x2 = 8
Último ponto da Região da
Solução em relação às retas da
Função Objetivo
6
x2
4
3
x14
8
2,25 3
Ponto Ótimo

49. 5º Encontrar os valores de x1 e x2
Como o Ponto Ótimo é o
encontro das retas, seus valores
podem ser encontrados através
da solução das inequações.
4x1 + 6x2 = 24
4x1 + 2x2 = 16
2x1 + 3x2 = 12
2x1 + x2 = 8
x2 = 8 - 2x1
2x1 + 3(8 - 2x1) = 12
2x1 + 24 - 6x1 = 12
-4x1 = -12
x1 = 3
Substituindo:
x2 = 2 6
x2
4
3
x14
8
2,25 3
Ponto Ótimo
/ 2

50. 6º Aplicar os valores de x1 e x2 na F.O.
Max L = 80x1 + 60x2
Max L = ( 80 * 3) + (60 * 2) = 360

52. Resolva graficamente:
Max L = 0,3x1 + 0,5x2
s.a.
2x1 + x2 < 2
x1 + 3x2 < 3
Não negatividade
x1, x2 > 0
Resposta:
x1 = 0,60
x2 = 0,80
L = 0,58

53. Resolva graficamente:
Max L = 4x1 + x2
s.a.
9x1 + x2 < 18
3x1 + x2 < 12
Não negatividade
x1, x2 > 0
Resposta:
x1 = 4
x2 = 1
L = 8

54. Resolva graficamente:
Max L = 0,3x1 + 0,5x2
s.a.
2x1 + x2 < 2
x1 + 3x2 < 3
Não negatividade
x1, x2 > 0
Resposta:
x1 = 0,6
x2 = 0,8
L = 0,58