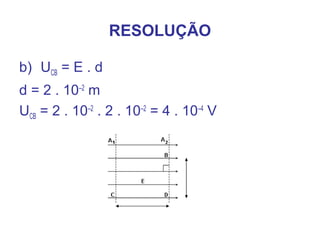
O documento aborda conceitos fundamentais sobre potencial elétrico, incluindo a definição de trabalho da força elétrica e diferenças de potencial entre pontos. Destaca a relação entre superfícies equipotenciais e campos elétricos, com exemplos numéricos de cálculo de potencial. Finalmente, apresenta exercícios para consolidar a compreensão dos tópicos discutidos.

1. POTENCIAL ELÉTRICO
FÍSICA

2. OBJETIVOS
• Potencial em ponto gerado por uma
carga;
• Trabalho da força elétrica;
• Diferença de potencial;
• Superfícies equipotenciais;
• Relação entre potencial elétrico e campo
elétrico uniforme

3. POTENCIAL ELÉTRICO
É uma medida associada a energia
potencial elétrica de uma carga em
determinado ponto.
Figura 1 Figura 2
q
E
V Pel
= PelE V.q=

4. POTENCIAL ELÉTRICO
É uma grandeza escalar. Será positivo se
Q > 0. Se Q < 0 será negativo.
K.Q
V
d
=

5. EXEMPLO
Um ponto P está no ponto médio da reta
que une duas cargas de mesmo módulo Q,
uma positiva e outra negativa. Determine o
potencial elétrico no referido ponto.

6. RESOLUÇÃO

7. EXERCÍCIO
(UFPE) - A figura a seguir mostra duas cargas
iguais q = 1,0 . 10–11 C, colocadas em dois
vértices de um triângulo eqüilátero de lado igual a
1 cm. Qual o valor, em volts, do potencial elétrico
no terceiro vértice do triângulo (ponto P)?

8. RESOLUÇÃO
VP = V1P + V2P =
VP = 2 . 9 . 109
. 10–11
. 102
= 18 V
1P 2P
kq kq
d d
+
9 11
P 2
2kq 2.9.10 .10
V
d 1.10
−
−
= =

9. TRABALHO REALIZADO POR UMA
FORÇA ELÉTRICA
W = F . d . cos θ

10. TRABALHO REALIZADO POR UMA
FORÇA ELÉTRICA
W = F . d . cos θ
WAB = Epel(A) - Epel(B)
WAB = VA . q – VB . q = (VA – VB) . q

11. DIFERENÇA DE POTENCIAL
O termo VA – VB é conhecido como diferença de
potencial (ddp) entre A e B e normalmente é
representado por UAB ou VAB.
Quando uma carga q é submetida a uma
diferença de potencial, ela entra em movimento,
pois a força elétrica realiza trabalho

12. SUPERFÍCIES EQUIPOTENCIAIS

13. SUPERFÍCIES EQUIPOTENCIAIS
• O campo elétrico é um campo de forças
conservativas, isto é, o trabalho realizado sobre
a carga é independente da trajetória percorrida.
• Percorrendo uma linha de força no seu sentido,
o potencial elétrico, ao longo de seus pontos,
diminui.

14. CAMPO ELÉTRICO UNIFORME E
POTENCIAL ELÉTRICO
W = F . d . cos θ
F = E.q e cos θ = 1
W = E.q.d.1
W = U.q
U.q = E.q.d
U = E.d

15. EXEMPLO
(UNIRIO 2000) - Sejam 2 superfícies equipotenciais A1 e A2, e um
campo elétrico uniforme de intensidade E = 2,0 . 10–2
N/C, conforme
mostra a figura a seguir.
As distâncias CD e DB são, respectivamente, 2,0 cm e 1,0 cm.
Determine:
a) o trabalho da força elétrica para conduzir uma carga q = 4,0 µC de
C até B;
b) a diferença de potencial entre C e B.

16. RESOLUÇÃO
a) WCD = UCD . q = E. d . q
WCD = 2 . 10–2
. 2 . 10–2
. 4 . 10-6
WCD = 16 . 10–10
= 1,6 . 10–9
J

17. RESOLUÇÃO
b) UCB = E . d
d = 2 . 10–2
m
UCB = 2 . 10–2
. 2 . 10–2
= 4 . 10–4
V

18. EXERCÍCIO
(UFRN) - A figura representa as linhas de força de
um campo elétrico. Com relação aos potenciais VA e
VB, e às intensidades do campo elétrico EA e EB, nos
pontos A e B, podemos afirmar que:
a)VA > VB; EA > EB
b)VA < VB; EA < EB
c)VA = VB; EA = EB
d)VA < VB; EA > EB
e)VA > VB; EA < EB

19. GABARITO: E