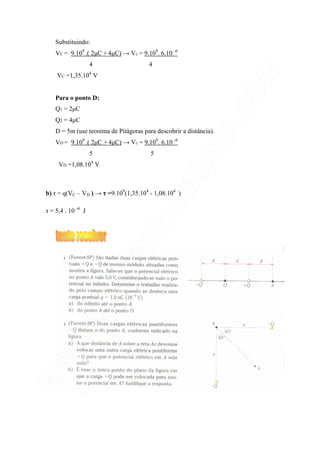
O documento discute o trabalho realizado por forças elétricas. Explica que o trabalho é igual à carga vezes a diferença de potencial entre dois pontos e que a diferença de potencial é proporcional à distância entre as cargas. Também apresenta fórmulas para calcular potencial elétrico e resolução de exercícios.

1. AULA 8
Trabalho da força elétrica
Se colocarmos uma carga q num local onde há campo elétrico E uniforme, surgirá uma
força elétrica F de interação entre eles.
Essa carga pode sofrer um deslocamento d, de direção do campo e de sentido
conforme o sinal da carga.
Em Mecânica, aprendemos que trabalho (τ ) é o produto da força pelo
deslocamento causado por essa força, isto é:
τ = F.d, mas como F = q.E, logo:
τ =q.E.d
Na figura abaixo, uma carga q é colocado em B onde há ação do campo elétrico
→
E . Como o campo é de afastamento e q>0, a força é de repulsão. Logo, q tende a se
afastar de B para A, deslocando uma distância d= dB - dA
Fig 1.Trabalho da força elétrica ao afastar de B para A.
Por outro lado, se quisermos aproximar duas cargas de mesmo sinal, precisamos aplicar
uma força externa para vencer a força de repulsão criada pelas cargas.
Essa força externa realizará um trabalho que mede a energia potencial
transferida do sistema. Eliminando a força externa, a força de repulsão elétrica
transformará a energia potencial elétrica em cinética, conforme o aumento da
velocidade de afastamento.

2. Chamamos de potencial elétrico(V), a grandeza que mede a capacidade de um campo
elétrico realizar trabalho.
O potencial elétrico é uma grandeza
escalar, o seu valor só depende do módulo
e do sinal da carga Q que origina o
campo.
Se Q > 0, V > 0
Se Q < 0, V < 0
Fig2. trabalho realizado pela força externa para aproximar a carga q. Fonte: FÍSICA- Alberto Gaspar.
A fórmula para calcular o potencial de em campo gerado por uma partícula Q é:
d
qQK
E
..
= A unidade de medida o
potencial elétrico é volts(V) no SI.
K= 9.109
N.m²
C²
q =módulo da carga de prova
d = distância, em metros(m), entre
Q(carga que origina o campo) e
q(carga de prova)
Potencial elétrico no ponto P
Pontencial elétrico no ponto P, é o próprio potencial numa distância d, a partir da
posição do Q tal que Vp = k.Q
dp
Se a distância dp → ∞(infinitamente afastado), então Vp = 0
Na figura 1. a diferença da intensidade do campo elétrico entre os pontos A e B, resulta
na diferença de potencial entre os pontos A e B.

3. A diferença de potencial entre A e B seria VA – VB = k.Q - k.Q
dA dB
Chamamos de U = VA – VB , temos τ = q(k.Q - k.Q) isto é: τ = q(VA – VB )
dA dB
Conclui-se que o trabalho da força elétrica é o produto da carga de prova q e a
diferença de potencial. Quanto maior a diferença de potencial entre os pontos,
maior é o trabalho realizado, daí a definição da diferença de potencial elétrico.
∆VAB = τAB
q
Lembramos também que o trabalho não depende da trajetória descrita pela carga
durante o seu deslocamento, mas o trabalho é positivo se a força elétrica e o
deslocamento tiverem o mesmo sentido e será negativa se tiverem o sentido contrário.
Exercícios resolvidos
Considere o campo elétrico gerado pela carga Q = 1,2. 10-8
C, no vácuo. Determine:
a) os potenciais elétricos nos pontos A e B indicados.
b) o trabalho da força elétrica que agem q = 1µC ao ser deslocada de A para B.
Dado: ko = 9.109
N.m²
C²
Resolução:
Dados:
Q = 1,2. 10-8
C;
dA = 0,4m
dB = 0,6m
q = 1µC = 1.10-6
C
ko = 9.109
N.m²
C²

4. a) Fórmula: VA = Ko.|Q| → VA = 9.109
. 1,2. 10-8
= 270V
dA 0,4
VB = Ko.|Q| → VB= 9.109
. 1,2. 10-8
= 180V
dB 0,6
b) τAB = q(VA – VB)→ τAB =1.10-6
(270 – 180)
τAB = 9.10-5
J
1. No campo de uma carga puntiforme Q= 3µC são dados dois pontos A e B cujas
distâncias à carga Q são respectivamente, dA = 0,3m e dB = 0,9m. O meio é vácuo.
Determine:
a)Potencial elétrico criado por várias cargas puntiformes.
b) O trabalho da força elétrica que atua em q = 5µC, ao ser deslocado de A para B.
c) O trabalho da carga q = 5µC ao ser deslocado de B para A.
Dado: ko = 9.109
N.m²
C²
Potencial elétrico criado por várias cargas puntiformes.
Como o potencial elétrico é uma grandeza que só depende do campo elétrico criado pela
carga Q, no ponto P, então o potencial criado por várias cargas são independentes
entre si, e o resultado no ponto P é a soma algébrica de cada um dos potenciais.

5. O potencial elétrico no ponto P da figura ao
lado é:
Vp = Ko.|Q1| + Ko.|Q2| +... + Ko.|Qn|
d1 d2 dn
Exercício resolvido
Determine o potencial elétrico resultante em P nos casos (a) e (b) indicados. Dados: Q =
1µC e d =0,3m. O meio é vácuo.
Resolução
Dados:
Q = 1µC = 1.10-6
C
D = 0,3m
: ko = 9.109
N.m²
C²
Fórmula: Vp = Ko.|Q1| + Ko.|Q2| +... + Ko.|Qn|
d1 d2 dn
a) Vp =9.109
. 1.10-6
+ 9.109
. 1.10-6
= 6.104
V
0,3 0,3
b) Vp =9.109
. 1.10-6
- 9.109
. 1.10-6
= 0 V
0,3 0,3
- Potencial elétrico é uma grandeza escalar, isto é, não tem direção nem sentido.
- A unidade de medida de trabalho é joules (J).

6. -A unidade de medida do potencial elétrico e da diferença de potencial é volts (V).
-Exercícios resolvidos
1.
1. (Vunesp) Na configuração de cargas abaixo, qual é a expressão que representa
potencial eletrostático no ponto P?
Resolução:
De acordo com a observação acima, queremos analisar o potencial criado por duas
cargas em um único ponto P. Então devemos somar o potencial de cada um.
Vp = k.q + k. –q → kq – 3.q = -2k.q
3.a a 3.a 3.a
2. Duas cargas elétricas puntiformes Q1 = 2µC e Q2 = 4µC estão fixas nos pontos A
e B, separados pela distância d = 8m, no vácuo. Determine (Dado: k = 9.109
N.m²/C):
a) potenciais elétricos resultantes nos pontos C e D.
b) O trabalho da força elétrica resultante que atua em q = 2, 0 10-7
C ao ser
levada de C para D.
Resolução:
a) Dados: Para o ponto C
Q1 = 2µC
Q2 = 4µC
D = 4m
VC = k. Q1 + k. Q2 → k.( Q1 + Q2)
d d d

7. Substituindo:
VC = 9.109
.( 2µC + 4µC) → Vc = 9.109
. 6.10 -6
4 4
VC =1,35.104
V
Para o ponto D:
Q1 = 2µC
Q2 = 4µC
D = 5m (use teorema de Pitágoras para descobrir a distância).
VD = 9.109
.( 2µC + 4µC) → Vc = 9.109
. 6.10 -6
5 5
VD =1,08.104
V
b) τ = q(VC – VD ) → τ =9.109
(1,35.104
- 1,08.104
)
τ = 5,4 . 10 -4
J

8. Respostas:
1. -5.10 -9
j; + 5. 10 -9
j
2. a)a/2; b qualquer ponto da circunferência de centro A e raio a/2
3. a) -3,6.104
V; b) 4,0.10-6
C