Baixado 45 vezes
Carregado porMário Henrique
Unidade ii física 13
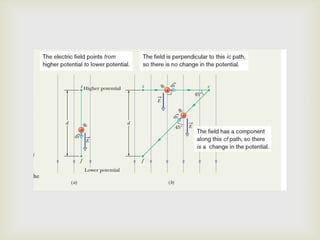
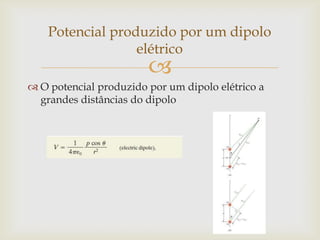
O documento discute conceitos fundamentais de potencial elétrico, incluindo: (1) definições de energia potencial elétrica, potencial elétrico e campo elétrico; (2) cálculo do potencial elétrico produzido por cargas pontuais e distribuições de cargas; e (3) relação entre potencial elétrico e campo elétrico.
Mais conteúdo relacionado
![Processo de Eletrização [Aula 01]](https://cdn.slidesharecdn.com/ss_thumbnails/processodeeletrizaoaula01-140119135406-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
Unidade ii física 13
- 1.
- 2. Grandeza Unidade Símbolo Energia potencial Joule J elétrica Potencial elétrico Volt V Campo Elétrico Volt/metro V/m
- 3.
- 4. Exemplo Trabalho e energiapotencial associados a um campo elétrico
- 6. Solução O trabalho é dado por A variação na energia potencial é dada por
- 7. Diferença de Potencial A diferença de potencial é definida como a energia potencial por unidade de carga: O potencial é uma característica, grandeza escalar, apenas do campo elétrico na região do espaço que está sendo investigada:
- 8. Exemplo Determinação da diferença de potencial a partir do campo elétrico
- 10. Solução
- 11. Potencial Produzido poruma carga pontual Uma partícula de carga positiva produz um potencial elétrico positivo; uma partícula de carga negativa produz um potencial elétrico negativo.
- 12. Potencial produzido porum grupo de cargas pontuais Nós calculamos separadamente os potenciais produzidos pelas cargas no ponto dado e somamos os potenciais. No caso de n cargas, o potencial total é dado por
- 13. Exemplo Potencial total de várias partículas carregadas
- 14. Solução O potencial elétrico é dado por
- 15. Exemplo O potencialnão é um vetor, então a orientação não é relevante (a) Na Figura, 12 elétrons (de carga –e) são mantidos fixos, com espaçamento uniforme, ao longo de uma circunferência de raio R. Tomando V=0 no infinito, quais são o potencial elétrico e o campo elétrico no centro C da circunferência? (b) Se os elétrons forem deslocados ao longo da circunferência até ficarem distribuídos com espaçamento desigual em um arco de 120° (Figura (b)), qual será o potencial elétrico no ponto C? O campo elétrico no ponto C sofrerá alguma mudança?
- 17. Solução (a) Como todos os elétrons possuem a mesma carga -e, e estão a mesma distância R, potencial elétrico é dado por Pela simetria do problema, o campo elétrico no ponto C é nulo
- 18. (b) O potencialelétrico continua a ser o mesmo, pois as cargas e as distâncias não mudaram. O novo campo elétrico no ponto C estará orientado na direção de algum ponto do arco de 120°.
- 19. Potencial produzido porum dipolo elétrico O potencial produzido por um dipolo elétrico a grandes distâncias do dipolo
- 20. Potencial produzido poruma distribuição contínua de cargas Para calcular o potencial elétrico fazemos uma integral sobre todos os elementos de carga
- 21. Linha de cargas O potencial elétrico de uma linha de cargas é dado por
- 22. Disco carregado O potencial elétrico de um disco carregado é dado por
- 23. 2.2 Cálculo doCampo Elétrico a partir do Potencial
- 24. Exemplo Cálculo docampo a partir do potencial O potencial elétrico em um ponto do eixo central de um disco uniformemente carregado é dado por A partir dessa equação, determine uma expressão para o campo elétrico em qualquer ponto do eixo do disco.
- 25. Solução A componente z é o negativo da taxa de variação do potencial com a distância z:
- 26. 2.3 Superfícies equipotenciais Pontos vizinhos que possuem o mesmo potencial elétrico formam uma superfície equipotencial. O campo elétrico não realiza nenhum trabalho líquido W sobre uma partícula carregada quando a partícula se desloca de um ponto para outro de uma superfície equipotencial. Por simetria, as superfícies equipotenciais produzidas por uma carga pontual ou por qualquer distribuição de cargas com simetria esférica constituem uma família de esferas concêntricas. No caso de um campo elétrico uniforme, as superfícies formam uma família de planos perpendiculares às linhas de campo. As superfícies equipotenciais são sempre perpendiculares às linhas de campo elétrico, e portanto, ao campo elétrico; que é tangente a essas linhas.
- 28. Energia potencial deum sistema de cargas pontuais A energia potencial elétrica de um sistema de cargas pontuais fixas é igual ao trabalho que deve ser executado por um agente externo para montar o sistema, começando com as cargas a uma distância infinita das outras.
- 29. Exemplo Energia Potencial de um sistema de três partículas carregadas
- 30. Solução A energia potencial total U do sistema de três cargas é a soma das energias potenciais associadas aos três pares de cargas:
- 31. Exemplo Conversão de energiacinética em energia potencial elétrica
- 33. Solução De acordo com a lei da conservação da energia mecânica
- 34. Potencial de umCondutor Carregado Uma carga em excesso colocada em um condutor se distribui na superfície do condutor de tal forma que o potencial é o mesmo em todos os pontos do condutor (tanto na superfície como no interior). Isto acontece mesmo que o condutor tenha uma cavidade interna e mesmo que a cavidade interna contenha uma carga elétrica.