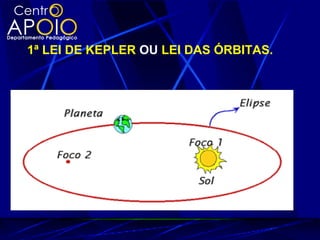
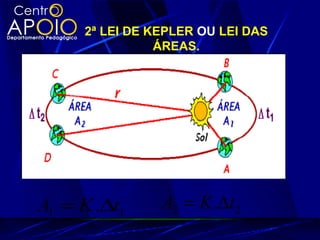
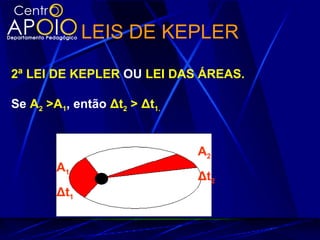
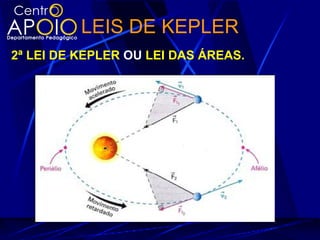
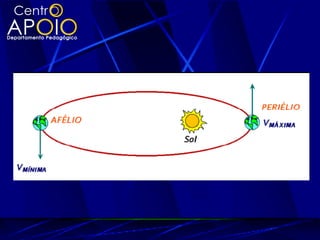
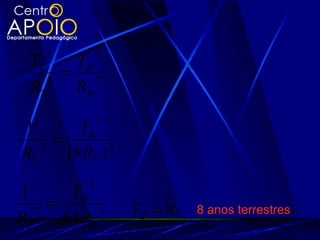
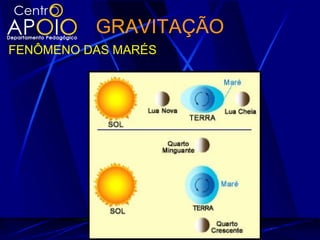
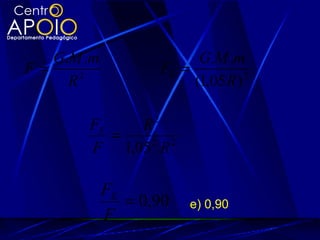
O documento explora a gravitação universal, detalhando as leis de Kepler que descrevem o movimento dos planetas e sua relação com a gravitação e as leis de Newton. As leis abordam aspectos como órbitas elípticas, áreas varridas em tempos iguais e a proporcionalidade entre o período orbital e o raio médio das órbitas. Também são discutidos conceitos como força gravitacional, energia potencial gravitação e velocidade de escape.

2. GRAVITAÇÃO UNIVERSAL
OBJETIVOS:
 Conhecer o movimento dos corpos celestes;
 Apresentar e discutir as leis de Kepler;
 Entender o que é a Lei da gravitação universal;
 Fazer relação entre gravitação e as Leis de Newton;
 Estudar algumas consequências da gravitação.

3. LEIS DE KEPLER
As leis de Kepler são Universais.
As três leis de Kepler que serão apresentadas são
universais, isto é, valem para o nosso sistema Solar e
também para qualquer outro sistema do Universo em
que exista uma grande massa central em torno da qual
gravitem massas menores.

4. LEIS DE KEPLER
1ª LEI DE KEPLER OU LEI DAS ÓRBITAS.
A trajetória dos planetas em torno do sol é
elíptica sendo que o Sol ocupa um dos focos da
elipse.

5. 1ª LEI DE KEPLER OU LEI DAS ÓRBITAS.

6. Gravitação
1a
Lei de
Kepler
Órbitas
elípticas

7. LEIS DE KEPLER
2ª LEI DE KEPLER OU LEI DAS ÁREAS.
O raio vetor (linha imaginária que vai do Sol até a
Terra) varre áreas proporcionais aos tempos, ou seja,
quanto maior a área varrida pelo raio vetor, maior será o
intervalo de tempo gasto.
tKA ∆= .
A: é a área
∆t: é o intervalo de tempo
K: é uma constante de proporcionalidade chamada de
velocidade areolar.

8. 2ª LEI DE KEPLER OU LEI DAS
ÁREAS.
11 . tKA ∆= 22 . tKA ∆=

9. LEIS DE KEPLER
2ª LEI DE KEPLER OU LEI DAS ÁREAS.
Se A2 >A1, então Δt2 > Δt1.
A1
Δt1
A2
Δt2

10. LEIS DE KEPLER
2ª LEI DE KEPLER OU LEI DAS ÁREAS.

11. LEIS DE KEPLER
2ª LEI DE KEPLER OU LEI DAS ÁREAS.
A velocidade da terra ao redor do sol varia,
sendo máxima no periélio e mínima no afélio.

12. Gravitação
1a
Lei de
Kepler
Órbitas
elípticas
2a
Lei de
Kepler
Áreas iguais
em tempos
iguais
Velocidade
de translação
da terra varia

13. EXERCÍCIOS
A segunda lei de Kepler permite concluir que:
a) o movimento de um planeta é acelerado quando ele
se desloca do afélio ao periélio.
b) o movimento de um planeta é acelerado quando ele
se desloca do periélio ao afélio.
c) a energia cinética de um planeta é constante em
toda sua órbita.
d) quanto mais afastado o planeta estiver do Sol,
maior será sua velocidade de translação.
e) a velocidade de translação de um planeta é mínima
no ponto mais próximo do Sol.

15. EXERCÍCIOS
A segunda lei de Kepler permite concluir que:
a) o movimento de um planeta é acelerado quando ele
se desloca do afélio ao periélio.
b) o movimento de um planeta é acelerado quando ele
se desloca do periélio ao afélio.
c) a energia cinética de um planeta é constante em
toda sua órbita.
d) quanto mais afastado o planeta estiver do Sol,
maior será sua velocidade de translação.
e) a velocidade de translação de um planeta é mínima
no ponto mais próximo do Sol.

16. EXERCÍCIOS
A segunda lei de Kepler permite concluir que:
a) o movimento de um planeta é acelerado quando ele
se desloca do afélio ao periélio.

17. EXERCÍCIOS
Considere que o esboço da elipse abaixo representa a
trajetória de um planeta em torno do Sol, que se
encontra em um dos focos da elipse. Em cada trecho, o
planeta é representado no ponto médio da trajetória
naquele trecho. As áreas sombreadas são todas iguais
e os vetores v1, v2, v3 e v4 representam as velocidades
do planeta nos pontos indicados.

18. Considerando as leis de Kepler afirma-se:
I. os tempos necessários para percorrer cada um dos
trechos sombreados são iguais.
II. o módulo da velocidade v1 é menor do que o módulo
da velocidade v2.
III. no trecho CD a aceleração tangencial do planeta tem
sentido contrário ao de sua velocidade
São corretas:
a) I e II b) I e III c) I somente d) todas

19. EXERCÍCIOS
Considere que o esboço da elipse abaixo
representa a trajetória de um planeta em torno do Sol,
que se encontra em um dos focos da elipse. Em cada
trecho, o planeta é representado no ponto médio da
trajetória naquele trecho. As áreas sombreadas são
todas iguais e os vetores v1, v2, v3 e v4 representam as
velocidades do planeta nos pontos indicados.

20. Considerando as leis de Kepler afirma-se:
I. os tempos necessários para percorrer cada um dos
trechos sombreados são iguais.
II. o módulo da velocidade v1 é menor do que o
módulo da velocidade v2.
III. no trecho CD a aceleração tangencial do planeta
tem sentido contrário ao de sua velocidade
São corretas:
a) I e II b) I e III c) I somente d) todas

21. a) I e II
b) I e III
c) I somente
d) todas
e) nenhuma

22. LEIS DE KEPLER
3ª LEI DE KEPLER OU LEI DOS PERÍODOS.
O cubo do período de um planeta (T) é
diretamente proporcional ao quadrado do raio da sua
órbita (R). Ou seja, é possível dizer: quanto mais
distante um planeta estiver do Sol, maior será seu
período.
23
.RKT =

23. Período dos planetas do sistema solar.
(d= dias e a= anos)

24. LEIS DE KEPLER
3ª LEI DE KEPLER OU LEI DOS PERÍODOS.
Calculando o período da órbita de um planeta
através do período da terra:
K
R
T
A
A
=2
3
K
R
T
B
B
=2
3
2
3
2
3
B
B
A
A
R
T
R
T
=

25. LEIS DE KEPLER
3ª LEI DE KEPLER OU LEI DOS PERÍODOS.
Calculando o período da órbita de um planeta
através do período da terra:

26. Gravitação
1a
Lei de
Kepler
Órbitas
elípticas
2a
Lei de
Kepler
Áreas iguais
em tempos
iguais
Velocidade
de translação
da terra varia
3a
Lei de
Kepler
Período ao cubo
diretamente
proporcional
quadrado do raio
raio de órbita
maiores tem
período
menores

27. EXERCÍCIOS
Um planeta apresenta raio médio de sua órbita
igual a oito vezes o raio médio da órbita terrestre. O
período desse planeta vale:
a)16 anos terrestres
b) 8 anos terrestres
c) 4 anos terrestres
d) 2 anos terrestres

28. EXERCÍCIOS
Um planeta apresenta raio médio de sua órbita
igual 8 vezes o raio médio da órbita terrestre. O período
desse planeta vale:
a)16 anos terrestres
b) 8 anos terrestres
c) 4 anos terrestres
d) 2 anos terrestres

29. 2
3
2
3
B
B
T
T
R
T
R
T
=
2
3
2
3
)8(
1
T
B
T
R
T
R
=
2
3
2
3
64
1
T
B
T R
T
R
= 8=BT 8 anos terrestres

30. GRAVITAÇÃO
Newton analisou as Leis de Kepler e suas
anotações de observação celeste, e observou que a
velocidade dos planetas ao redor do sol variava. Como
a variação de velocidade é devido forças, Newton
concluiu que os planetas e o Sol interagem a distância,
com forças chamadas de gravitacionais.

31. GRAVITAÇÃO
LEI DA GRAVITAÇÃO UNIVERSAL.
Matéria atrai matéria na razão direta do produto
das massas e inversa do quadrado da distância.

32. GRAVITAÇÃO
LEI DA GRAVITAÇÃO UNIVERSAL.
Matéria atrai matéria na razão direta do produto
das massas e inversa do quadrado da distância.
2
..
d
mMG
FG =
G = 6,67. 10-11
N.m2
/kg2
(constante da gravitação universal).

33. GRAVITAÇÃO
FENÔMENO DAS MARÉS

34. Gravitação
1a
Lei de
Kepler
Órbitas
elípticas
2a
Lei de
Kepler
Áreas iguais
em tempos
iguais
Velocidade
de translação
da terra varia
3a
Lei de
Kepler
Período ao cubo
diretamente
proporcional
quadrado do raio
raio de órbita
maiores tem
período
menores
Força
gravitacional

35. Exercício
(Fuvest-SP) A Estação Espacial Internacional, que está
sendo construída num esforço conjunto de diversos
países, deverá orbitar a uma distância do centro da
Terra igual a 1,05 do raio médio da Terra. A razão R =
Fe/F, entre a força Fe com que a Terra atrai um corpo
nessa Estação e a força F com que a Terra atrai o
mesmo corpo na superfície da Terra, é
aproximadamente de:
a) 0,02 b) 0,05 c) 0,10 d) 0,50 e) 0,90

36. Exercício
(Fuvest-SP) A Estação Espacial Internacional, que está
sendo construída num esforço conjunto de diversos
países, deverá orbitar a uma distância do centro da
Terra igual a 1,05 do raio médio da Terra. A razão R =
Fe/F, entre a força Fe com que a Terra atrai um corpo
nessa Estação e a força F com que a Terra atrai o
mesmo corpo na superfície da Terra, é
aproximadamente de:
a) 0,02 b) 0,05 c) 0,10 d) 0,50 e) 0,90

37. 2
..
R
mMG
F = 2
)05,1(
..
R
mMG
FE =
22
2
.05,1 R
R
F
FE
=
90,0=
F
FE
e) 0,90

38. Gravitação
1a
Lei de
Kepler
Órbitas
elípticas
2a
Lei de
Kepler
Áreas iguais
em tempos
iguais
Velocidade
de translação
da terra varia
3a
Lei de
Kepler
Período ao cubo
diretamente
proporcional
quadrado do raio
raio de órbita
maiores tem
período
menores
Força
gravitacional
Força Peso Ação e reação

39. ENERGIA POTENCIAL GRAVITACIONAL
Adotando-se o nível zero (referencial no infinito),
demonstra-se que a energia potencial gravitacional de
um corpo, a uma distância d da Terra em relação ao
centro gravitacional da Terra, é:
d
mMG
EG
..
−=

40. Gravitação
1a
Lei de
Kepler
Órbitas
elípticas
2a
Lei de
Kepler
Áreas iguais
em tempos
iguais
Velocidade
de translação
da terra varia
3a
Lei de
Kepler
Período ao cubo
diretamente
proporcional
quadrado do raio
raio de órbita
maiores tem
período
menores
Força
gravitacional
Força Peso Ação e reação
Energia
potencial
gravitacional

41. VELOCIDADE DE ESCAPE.
É a menor velocidade com que se deve lançar um
corpo da superfície terrestre para que este se livre da
atração da Terra, isto é, chegue ao infinito com
velocidade nula
R
MG
v
..2
=
R é o raio da terra
M é a massa da terra

42. Gravitação
1a
Lei de
Kepler
Órbitas
elípticas
2a
Lei de
Kepler
Áreas iguais
em tempos
iguais
Velocidade
de translação
da terra varia
3a
Lei de
Kepler
Período ao cubo
diretamente
proporcional
quadrado do raio
raio de órbita
maiores tem
período
menores
Força
gravitacional
Força Peso Ação e reação
Energia
potencial
gravitacional
Velocidade
de escape

43. CORPOS EM ÓRBITA.
Num corpo (satélite) em órbita circular de raio r,
em torno de um planeta, a força gravitacional sobre ele
é a resultante centrípeta. Fcp = FG
r
MG
v
.
=

44. Gravitação
1a
Lei de
Kepler
Órbitas
elípticas
2a
Lei de
Kepler
Áreas iguais
em tempos
iguais
Velocidade
de translação
da terra varia
3a
Lei de
Kepler
Período ao cubo
diretamente
proporcional
quadrado do raio
raio de órbita
maiores tem
período
menores
Força
gravitacional
Força Peso Ação e reação
Energia
potencial
gravitacional
Velocidade
de escape
Força
gravitacional
Força
centrípeta
Velocidade
de órbita

45. Considere um satélite artificial em órbita circular..
Duplicando a massa do satélite sem alterar o seu
período de revolução, o raio da órbita será:
a) duplicado.
b) quadruplicado.
c) reduzido à metade.
d) reduzido à Quarta parte.
e) o mesmo.
Exercício

46. Considere um satélite artificial em órbita circular.
Duplicando a massa do satélite sem alterar o seu
período de revolução, o raio da órbita será:
a) duplicado.
b) quadruplicado.
c) reduzido à metade.
d) reduzido à Quarta parte.
e) o mesmo.
Exercício

47. e) o mesmo.
Exercício

48. Bibliografia
Ramalho, Nicolau e Toledo. Os fundamentos da física.
Mecânica, ed. Moderna. 7a
edição.
Halliday, Resnick, Walker. Fundamentos de física.
Gravitação, ondas e termodinâmica, ed. LTC, 3a
edição.