O documento discute o paradigma funcional de programação, apresentando conceitos como:
1) Linguagens funcionais onde variáveis não mudam de valor durante a execução;
2) Funções como valores de primeira classe que podem ser passadas como argumentos;
3) Uso de recursão para definição de funções.









![Exemplo - Quick sort (Haskell)
qs [] = []
qs (x:xs) = qs [y | y <- xs, y < x]
++ [x]
++ qs [y | y <- xs, y >= x]](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-12-320.jpg)
![Exemplo - Quick sort (C)
int particao(int vec[], int inicio, int
fim) {
int i, j;
i = inicio;
for (j = inicio + 1; j <= fim; ++j) {
if (vec[j] < vec[inicio]) {
++i;
troca(&vec[i], &vec[j]);
}
}
troca(&vec[inicio], &vec[i]);
return i;
}](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-13-320.jpg)
![Exemplo - Quick sort (C)
void quickSort(int vec[], int inicio,
int fim)
{
int p;
if (fim > inicio) {
p = particao(vec, inicio, fim);
quickSort(vec, inicio, p - 1);
quickSort(vec, p + 1, fim);
}](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-14-320.jpg)









![Expressões
● Literais:
-3.459
True
'a'
"hello"
[1,2,4,9]
● Aplicação de funções:
even 47
twice (-2)](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-24-320.jpg)





![Toda expressão tem um tipo
Os tipos podem ser inferidos
Prelude> :t (4 > 5)
(4 > 5) :: Bool
Prelude> :t (5+4)
(5+4) :: (Num t) => t
Prelude> :t [1.2,5.0]
[1.2,5.0] :: (Fractional t) => [t]](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-30-320.jpg)




![Funções como valores de primeira classe
Significa que as funções têm um estatuto tão importante como o dos inteiros, reais,
e outros tipos predefinidos. Concretamente, numa linguagem funcional as funções
podem ...
● Ser passadas como argumento para outras funções;
● Podem ser retornadas por outras funções;
● Podem ser usadas como elementos constituintes de estruturas de dados;
Prelude>map (x->2*x) [1,2,3]
[2,4,6]](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-35-320.jpg)




![Listas
Uma lista é composta sempre de dois segmentos: cabeça
(head) e corpo (tail). A cabeça é sempre o primeiro emento e
corpo é uma lista com os demais elementos.
Prelude> ['a','b','c','d']
"abcd"
Prelude> 'a':['b','c','d']
"abcd"](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-40-320.jpg)
![Listas em Haskell
●
● Três tipos de notação:
● construtores:
1 : 1 : 2 : 3 : 5 : 8 : []
● “colchetes":
[1, 1, 2, 3, 5, 8]
● strings (apenas para listas de caracteres):
['h', 'e', 'l', 'l', 'o'] = "hello"](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-41-320.jpg)
![Listas
Pode se definir uma lista indicando os limites inferior e superior:
[<limite-inferior> .. <limite-superior>]](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-42-320.jpg)
![Listas
Podemos definir qualquer progressão aritmética em uma lista utilizando a
seguinte notação:
[<termo1>, <termo2> .. <limite-superior>
Prelude> [0,3..21]
[0,3,6,9,12,15,18,21]
Prelude> [0,2..20]
[0,2,4,6,8,10,12,14,16,18,20]](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-43-320.jpg)
![Listas por compreensão
A definição de listas por compreensão é feita por um construtor de listas
que utiliza conceitos e notações da teoria dos conjuntos. Assim, para um
conjunto A temos:
Sendo E(x) uma expressão em X, onde X pertence a lista, dados um
conjunto de proposições Pi(x)
A = [E(x) | x <- lista, P1(x), ..., Pn(x)]
Por exemplo:
[x | x <- l1, even x, x < 100 ], todos pares menos que 100 pertencentes a l1](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-44-320.jpg)
![Compreensão de listas
● Um construtor de processamento de listas em linguagem de programação, a
notação matemática é a seguinte:
● Outros exemplos
● Por exemplo, as 10 primeiras potências de 2:
[2 ^ x | x <- [1..10] ]
● Todos os números pares maiores que 1 e menores que 100:
[ x | x <- [1..100] , par x ]](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-45-320.jpg)
![Exemplo:
[x | x <- [1..1000], even x, x < 100 ]
[2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,
46,48,50,52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,8
4,86,88,90,92,94,96,98]
Compreensão de listas](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-46-320.jpg)

![isempty :: [a] -> Bool
isempty [] = True
isempty anythingElse = False
length [] = 0
length (x : xs) = 1 + length xs
head [] = error "head []"
head (x:xs) = x
Casamento de padrões (lista)](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-48-320.jpg)
![Recursão
length :: [a] -> Int
length [] = 0
length (x : xs) = 1 + length xs
Um conceito básico em Haskell é o uso de recursão para
definição de funções](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-49-320.jpg)

![Recursão
●
A soma dos números de uma lista vazia
sumAll (x : xs) = x + sumAll xs
sumAll [] = 0
sumAll :: [Integer] -> Integer
Soma de todos os números de uma lista
Soma dos números de uma lista x : xs](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-51-320.jpg)
![Recursão
●
Concatenar uma lista vazia:
concat (s : ss) = s ++ concat ss
concat [] = [] --- = “”
concat :: [[Char]] -> [Char]
Concatenação de listas de caracteres
Concatenar uma lista a partir de um elemento:](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-52-320.jpg)
![Avaliação de Funções Recursivas
length [] = 0
length (x : xs) = 1 + (length xs)
length (1 : 2 : 4 : [])
1 + length (2 : 4 : [])
1 + 1 + length (4 : [])
1 + 1 + 1 + length []
1 + 1 + 1 + 0](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-53-320.jpg)


![Sinônimos
type Point = (Int, Int)
type Polygon = [Point]
p1 :: Point
p1 = (1,4)
pol1:: Polygon
pol1 = [(1,1),(1,2),(3,1),(1,1)]
56
Em Haskell, é possível criar sinônimos de tipos, ex:](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-56-320.jpg)





![Map
map :: (a -> b) -> [a] -> [b]
Main> map double [1,3,5,7]
[2,6,10,14]
62
A função map aplica uma função a todos os elementos de
uma lista.](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-62-320.jpg)
![Map pode ser definido por recursão ou por compreensão de
listas
Ou por compreensão de lista
Map
map :: (a -> b) -> [a] -> [b]
map f xs = [f x | x xs]
map :: (a -> b) -> [a] -> [b]
map f [] = []
map f (x : xs) = (f x) : map f xs
63](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-63-320.jpg)
![ghci> map (+3) [1,5,3,1,6]
[4,8,6,4,9]
ghci> map (++ "!") ["BIFF", "BANG", "POW"]
["BIFF!","BANG!","POW!"]
ghci> map (replicate 3) [3..6]
[[3,3,3],[4,4,4],[5,5,5],[6,6,6]]
ghci> map (map (^2)) [[1,2],[3,4,5,6],[7,8]]
[[1,4],[9,16,25,36],[49,64]]
ghci> map fst [(1,2),(3,5),(6,3),(2,6),(2,5)]
[1,3,6,2,2]
64
Map](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-64-320.jpg)
![Map com avaliação parcial
Main> map (*5) [1,3,5,7]
[5,15,25,35]
incAll = map (1 +)
addNewlines = map (++ "n")
halveAll = map (/2)
squareAll = map (^2)
stringify = map (: [])
65](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-65-320.jpg)
![Filter
filter :: (a -> Bool) -> [a] -> [a]
Main> filter even [1..10]
[2,4,6,8,10]
66
A função filter seleciona os elementos de uma lista que
satisfazem a um predicado](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-66-320.jpg)
![Filter
filter :: (a -> Bool) -> [a] -> [a]
filter p xs = [x | x <- xs, p x]
filter p [] = []
filter p (x : xs)
| p x = x : filter p xs
| otherwise = filter p xs
67
Pode ser definido como compreensão de listas ou por recursão](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-67-320.jpg)
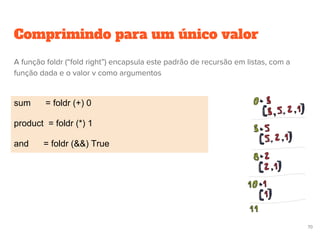
![Comprimindo para um único valor
f [] = v
f (x:xs) = x <- f xs
68
Um grande número de funções em listas podem ser definidas a partir de um
padrão simples de recursão
●A lista vazia recebe para um valor final, e uma lista
●não vazia é mapeada para um operador : que
●combina o primeiro elemento com a aplicação da função no resto da lista](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-68-320.jpg)
![Comprimindo para um único valor
sum [] = 0
sum (x:xs) = x + sum xs
product [] = 1
product (x:xs) = x * product xs
and [] = True
and (x:xs) = x && and xs
11/4/11 69](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-69-320.jpg)
![Definição do foldr
foldr::(a -> b -> b) -> b -> [a] -> b
foldr f v [] = v
foldr f v (x:xs) =
f x (foldr f v xs)
71](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-71-320.jpg)


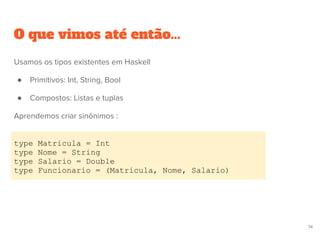

![Qual o problema com os sinônimos?
76
type Matricula = Int
type Nome = String
type Salario = Double
type Funcionario = (Matricula, Nome, Salario)
funcionarios :: [Funcionario]
funcionarios = [(1235,"joao", 580), (256,"jose", 590)]
aumentaSalario :: Funcionario -> Funcionario
aumentaSalario (m,n,s) = (m,n,s+(0.1*s))
type Nota = Double
type Alunos = (Matricula, Nome, Nota)
alunos :: [Alunos]
alunos = [(1,"antonio", 50.6), (6,"maria", 70)]
– eu poderia aplicar aumentaSalario a um aluno, pois são a mesma tupla,
– apenas com nomes diferentes](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-76-320.jpg)


![Tipos algébricos
data InfoLivro = Livro Int String [String]
Nome do tipo
Construtor de tipo
Diferenças entre nome de tipos e construtor de tipos:
O nome do tipo e dos construtores não precisa ser iguais.](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-79-320.jpg)
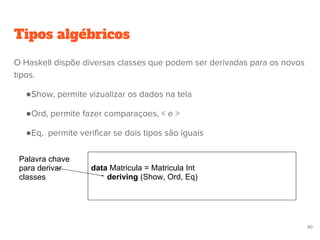






![União Disjunta – Tratando erro
data Maybe a = Nothing | Just a
87
Em Haskell existe um tipo de dado muito util em casos onde uma função pode não
ter retorno.
●ex. buscar um elemento em uma lista
type Aluno = (Int, String)
busca :: Int -> [Aluno] -> Maybe String
busca mat [] = Nothing
busca mat ((x,y):xys)
| mat == x = Just y
| otherwise = busca mat xys](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-87-320.jpg)







![● Uma característica importante de Haskell é o uso de tipos paramétricos
● Muitas funções podem ser definidas em termos de tipos genéricos
● Convenção: usamos a, b, c para tipos genéricos
● Tipos paramétricos comuns, listas e tuplas
length :: [a] → Int
Tipos Paramétricos em Haskell
Pode ser lista de inteiros, de listas ..
95](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-95-320.jpg)



![Restrição no polimorfismo
somatodos :: [a] -> a
somatodos (x:xs) = x + somatodos xs
99
Esta função pode ser aplicada a qualquer tipo ?](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-99-320.jpg)
![Restrição no polimorfismo
somatodos :: (Num a) => [a] -> a
somatodos (x:xs) = x + somatodos xs
100
Usando “type classes
A função somatodos funciona sobre qualquer “a”, desde que ele seja um Num.](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-100-320.jpg)






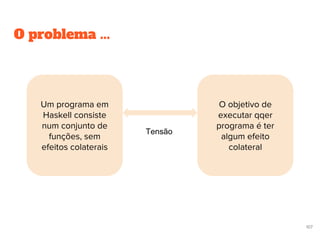
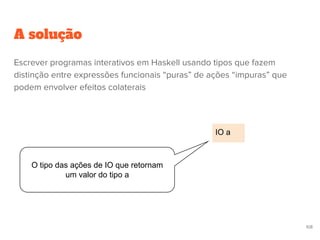
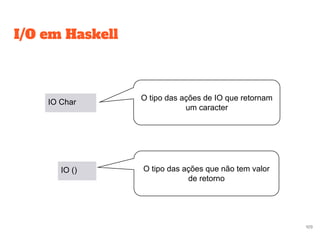






![Funções para string
117
Função lines, quebra uma string pelo marcador de fim de linha
lines “linha1nlinha2”
= [“linha1”,linha 2]
Função words, quebra uma string por separador de palavras,”espaço”.
words “uma frase”
= [“uma”, frase]](https://image.slidesharecdn.com/pfapresentacaov2-120418200921-phpapp01/85/Paradigma-Funcional-Caso-de-Estudo-Haskell-117-320.jpg)

