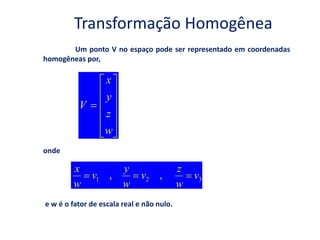
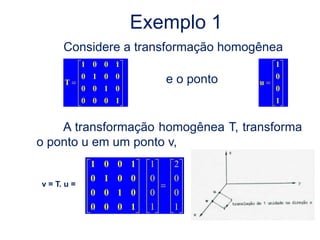
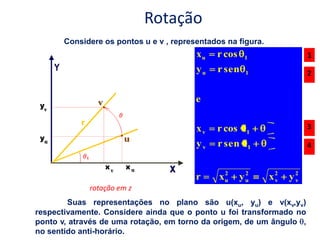
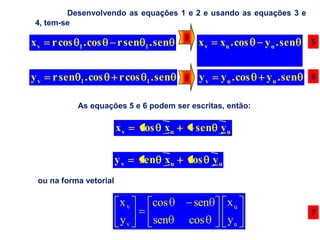
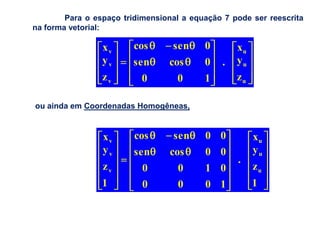
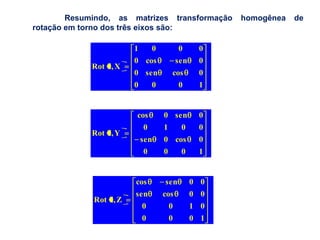
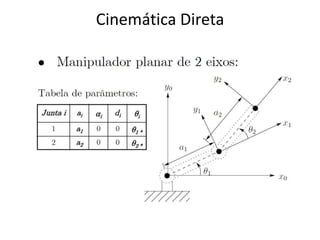
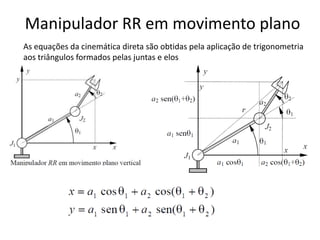
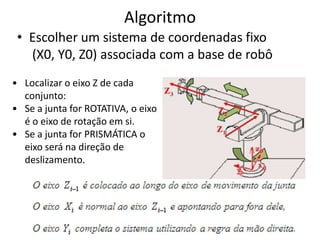
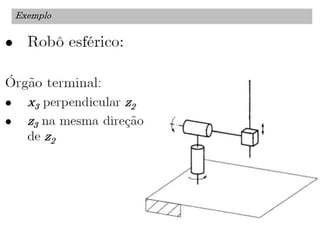
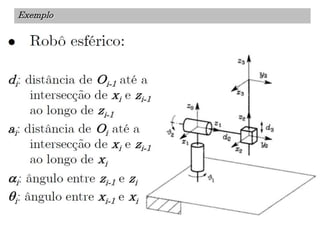
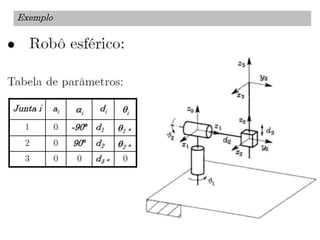
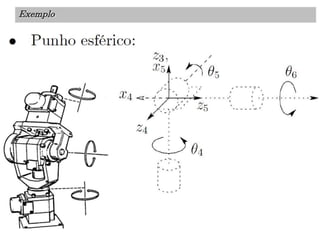
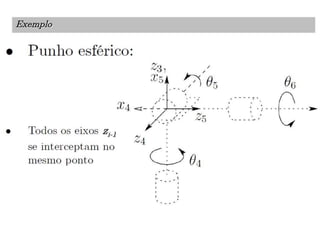
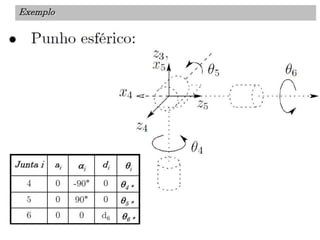
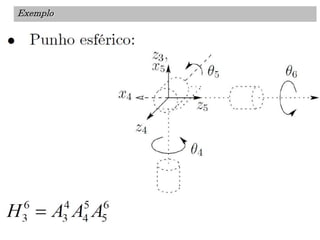
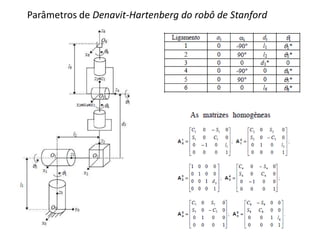
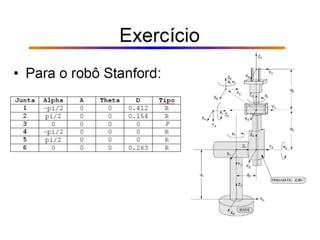
O documento discute a notação de Denavit-Hartenberg para representar a cinemática de robôs. Ele explica como escolher os sistemas de coordenadas para cada junta e como os parâmetros de Denavit-Hartenberg (a, α, d e θ) definem a posição relativa entre sistemas de coordenadas consecutivos. Também aborda exceções à notação e como aplicá-la para obter as equações da cinemática direta de um robô.

1. ROBÓTICA
Cinemática Direta
Parâmetros D-H
Lucélio de Oliveira Lemos

2. Sistemas de Referência
e
Transformação de Coordenadas

3. Transformação Homogênea
Um ponto V no espaço pode ser representado em coordenadas
homogêneas por,
x
y
V
z
w
onde
x y z
v1 , v2 , v3
w w w
e w é o fator de escala real e não nulo.

4. Translação
É Possível transladar um ponto u nas
direções X, Y, e Z ou em uma direção arbitrária, a
partir da aplicação da relação
v=T.u
com a relação
1 0 0 x0
0 1 0 y0
T trans(x 0 , y 0 , z 0 )
0 0 1 z0
0 0 0 1

5. Exemplo 1
Considere a transformação homogênea
1 0 0 1 1
0 1 0 0 0
T e o ponto u
0 0 1 0 0
0 0 0 1 1
A transformação homogênea T, transforma
o ponto u em um ponto v,
1 0 0 1 1 2
0 1 0 0 0 0
v = T. u =
0 0 1 0 0 0
0 0 0 1 1 1

6. Exemplo 2
Transladar o ponto u(1,0,0) de 1 unidade na direção X, 2 na
direção Y e 3 na direção Z.
1 0 0 1 1
0 1 0 2 0
v trans (1,2,3)
0 0 1 3 0
0 0 0 1 1

7. Rotação
Considere os pontos u e v , representados na figura.
xu r cos 1 1
yu r sen 1 2
e
xv r cos 3
1
yv r sen 1 4
2 2
r xu yu x2
v y2
v
rotação em z
Suas representações no plano são u(xu, yu) e v(xv,yv)
respectivamente. Considere ainda que o ponto u foi transformado no
ponto v, através de uma rotação, em torno da origem, de um ângulo ,
no sentido anti-horário.

8. Desenvolvendo as equações 1 e 2 e usando as equações 3 e
4, tem-se
xv r cos 1 . cos r sen 1 . sen xv xu . cos y u . sen 5
yv r sen 1 . cos r cos 1 . sen yv y u . cos y u . sen 6
As equações 5 e 6 podem ser escritas, então:
xv cos xu sen y u
yv sen xu cos y u
ou na forma vetorial
xv cos sen xu
7
yv sen cos yu

9. Para o espaço tridimensional a equação 7 pode ser reescrita
na forma vetorial:
xv cos sen 0 xu
yv sen cos 0 . yu
zv 0 0 1 zu
ou ainda em Coordenadas Homogêneas,
xv cos sen 0 0 xu
yv sen cos 0 0 yu
.
zv 0 0 1 0 zu
1 0 0 0 1 1

10. Resumindo, as matrizes transformação homogênea de
rotação em torno dos três eixos são:
1 0 0 0
0 cos sen 0
Rot , X
0 sen cos 0
0 0 0 1
cos 0 sen 0
0 1 0 0
Rot , Y
sen 0 cos 0
0 0 0 1
cos sen 0 0
sen cos 0 0
Rot , Z
0 0 1 0
0 0 0 1

11. Cinemática Direta

12. Cinemática Direta

13. Manipulador RR em movimento plano
As equações da cinemática direta são obtidas pela aplicação de trigonometria
aos triângulos formados pelas juntas e elos

14. Notação de
Denavit-Hartemberg

15. Notação de
Denavit-Hartemberg

16. Algoritmo
• Escolher um sistema de coordenadas fixo
(X0, Y0, Z0) associada com a base de robô
• Localizar o eixo Z de cada
conjunto:
• Se a junta for ROTATIVA, o eixo
é o eixo de rotação em si.
• Se a junta for PRISMÁTICA o
eixo será na direção de
deslizamento.

18. Algoritmo

19. Notação de
Denavit-Hartemberg
A posição relativa entre dois sistemas de coordenadas consecutivos, sistemas
Oi−1-xi−1yi−1zi−1 e Oi-xiyizi, é completamente determinada pelas posições relativas
entre os eixos xi−1 e xi, e entre os eixos zi e zi−1, que são definidas pelos quatro
parâmetros seguintes:
• ai: é a distância (em módulo) entre zi−1 e zi, medida ao longo do eixo xi, que é a
normal comum entre zi−1 e zi, ou seja, é a distância HiOi;
• αi: é o ângulo (com sinal) entre o eixo zi−1 e o eixo zi, medido em torno do eixo xi,
segundo a regra da mão direita, ou seja, é o ângulo de rotação em torno do eixo xi,
que o eixo zi−1 deve girar para que fique paralelo ao eixo zi;
• di: é a distância (com sinal) entre os eixos xi−1 e xi, medida sobre o eixo zi−1 (que é a
normal comum entre xi−1 e xi), partindo-se de Oi−1 e indo em direção à Hi. O sinal
de di é positivo, se para ir de Oi−1 até Hi, caminha-se no sentido positivo de zi−1, e
negativo, se caminha-se no sentido oposto de zi−1;
• θi: é o ângulo (com sinal) entre o eixo xi−1 e o eixo xi, medido em torno do eixo zi−1,
segundo a regra da mão direita, ou seja, é o ângulo de rotação em torno do eixo zi−1,
que o eixo xi−1 deve girar para que fique paralelo ao eixo xi.

20. Notação de
Denavit-Hartemberg
Com estes quatro parâmetros, a posição e orientação do sistema de coordenadas i
em
relação ao sistema i−1 pode ser definida como uma sequência de quatro
transformações:
• A primeira transformação, consiste em uma rotação em torno de zi−1, de um
ângulo θi , medido segundo a regra da mão direita, de forma a alinhar xi−1 com xi:
• A segunda transformação, é uma translação ao longo do eixo zi−1, de uma distância
di, medida a partir do ponto Oi−1, até encontrar a intercessão da normal comum
entre zi−1 e zi (ponto Hi);
• A terceira transformação, consiste em uma translação ao longo do eixo xi, de uma
distância ai, partindo-se do ponto Hi até encontrar o eixo zi (ponto Oi); e
• A quarta transformação consiste em uma rotação em torno do eixo xi, de um
ângulo αi, medido segundo a regra da mão direita, de forma a alinhar o eixo zi−1 com
o eixo zi.

21. Notação de
Denavit-Hartemberg
Assim, tem-se, em resumo, as seguintes transformações:
onde os símbolos Rot e Trans significam respectivamente transformação de rotação e de
translação. Em termos de transformações homogêneas, tem-se o seguinte:
Os parâmetros ai e αi são constantes e são determinados pela geometria do ligamento i.
Um dos outros dois parâmetros, di ou θi, varia a medida que a articulação se move.

22. Notação de
Denavit-Hartemberg
Existem algumas exceções à notação de Denavit-Hartenberg, sendo estas as seguintes:
• Para estabelecer o sistema de coordenadas da base, a origem do sistema pode ser
escolhida em qualquer ponto do eixo z0. Os eixos x0 e y0, podem ser escolhidos
arbitrariamente, desde que satisfaçam a regra da mão direita;
• Para estabelecer o sistema de coordenadas do efetuador, a origem do sistema pode
ser escolhida em qualquer ponto conveniente do efetuador. A orientação dos eixos
deve ser tal que xn seja perpendicular a zn−1;
• Se os eixos das duas articulações de um ligamento são paralelos, a normal comum
entre eles não é única. Neste caso, a direção de xi−1 deve ser perpendicular a ambos
os eixos e a origem Oi é arbitrária;
• Se os eixos das duas articulações de um ligamento se interceptam, ou seja, se zi−1
intercepta zi, a origem Oi deve ser localizada na interseção dos dois eixos e xi deve
ser perpendicular a ambos os eixos.

31. Parâmetros de Denavit-Hartenberg do robô de Stanford