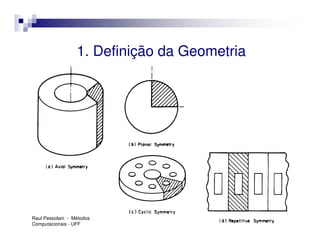
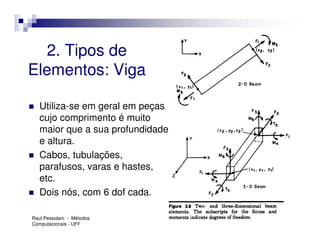
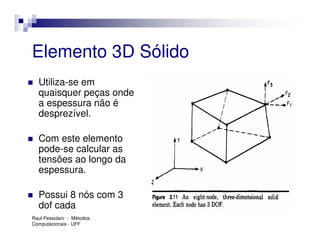
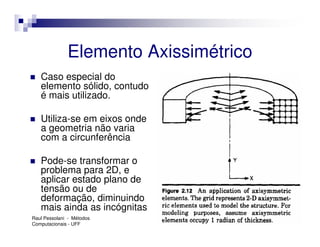
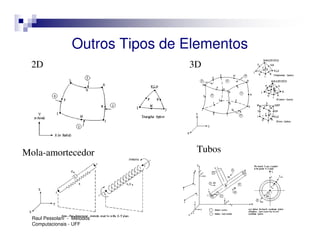
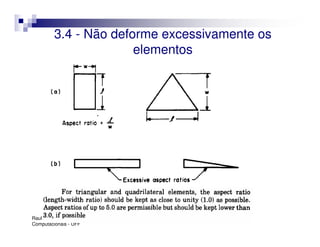
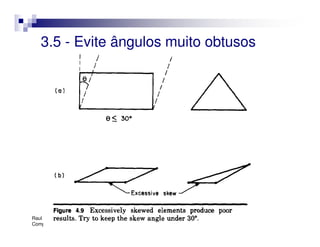
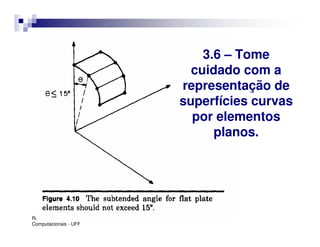
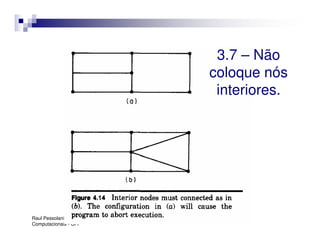
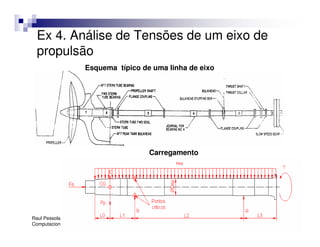
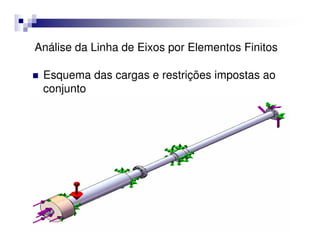
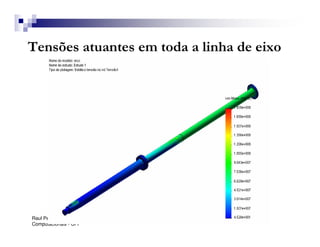
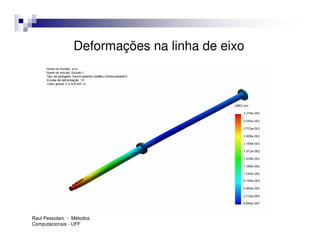
O documento introduz o Método dos Elementos Finitos (MEF) como uma técnica para resolver equações diferenciais através da aproximação da solução contínua por soluções discretas em elementos distribuídos. Explica as etapas do MEF, incluindo a modelagem, discretização, resolução do sistema algébrico e análise dos resultados. Apresenta exemplos de aplicação do MEF em diversos problemas de engenharia.


![Seja a eq. de Poisson, que é uma eq. dif. de 2ª ordem que
descreve uma gde variedade de fenômenos:
2 ∂2Φ(x, ∂2Φ(x,
y) y)
∇ Φ(x, =
y) + =0.
2 2
∂x ∂y
O MEF a transforma num sistema de equações algébricas
que podem resolvidas facilmente pelo computador:
[ A ]{X }= {B }
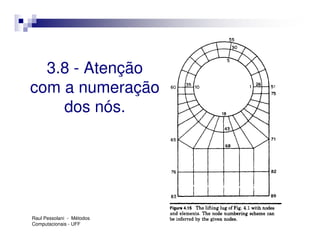
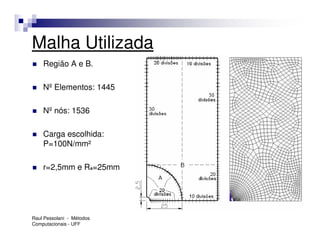
A ordem do sistema depende da malha adotada: do número de nós
e de graus de liberdade por nó.
As incógnitas podem ser temperatura, deslocamentos, tensões,
potencial elétrico, ....
Raul Pessolani - Métodos
Computacionais - UFF](https://image.slidesharecdn.com/modelagemmef-100923072957-phpapp02/85/Modelagem-mef-3-320.jpg)