Sae 2004-a

1
Prof. Avelino Alves Filho
NCE Núcleo de Cálculos Especiais S/C Ltda.
www.nce.com.br
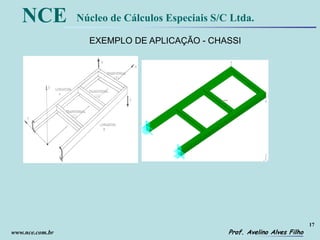
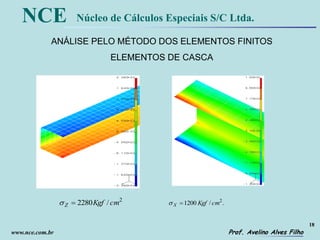
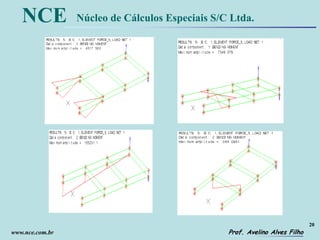
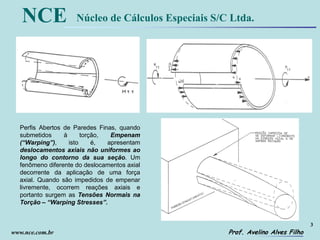
Análise de Estruturas compostas por perfis
abertos de Paredes Delgadas: Uma Aplicação
da Analogia Flexão-Retorção
Eng. Avelino Alves Filho, Prof Dr.

2
www.nce.com.br
O presente trabalho aborda os efeitos decorrentes do empenamento
(retorção) em perfis abertos de paredes delgadas,
que são amplamente utilizados em estruturas veiculares
Resolução do problema prático de flexo-torção :
•Introdução da Analogia Flexão-Retorção
•Cálculo das tensões normais devido à torção em
estruturas tipo grelha (chassi de veículos) por
intermédio de um modelo em elementos finitos com
reduzido número de graus de liberdade

3
www.nce.com.br
Perfis Abertos de Paredes Finas, quando
submetidos à torção, Empenam
(“Warping”), isto é, apresentam
deslocamentos axiais não uniformes ao
longo do contorno da sua seção. Um
fenômeno diferente do deslocamentos axial
decorrente da aplicação de uma força
axial. Quando são impedidos de empenar
livremente, ocorrem reações axiais e
portanto surgem as Tensões Normais na
Torção – “Warping Stresses”.

4
www.nce.com.br
TEORIA DE VLASOV: O Problema da Retorção
Bimomento de Flexo-Torção
No perfil aberto acima, é como se dois momentos fletores caminhassem na seção, um
em cada aba, daí surge o conceito de BIMOMENTO DE FLEXO-TORÇÃO (B).

5
www.nce.com.br
Durante a torção da barra, as seções transversais giram em relação ao Centro de
Torção C . Se não há restrição ao livre empenamento, a torção de qualquer tipo de
seção - aberta ou fechada - é governada pela equação
dx
d
IGM tx

..
A conhecida Torção de Saint
Venant

6
www.nce.com.br
Quando o perfil está submetido à Torção Restringida –
impedimento de se empenar livremente, existe uma resistência
adicional ao momento torçor Mx, e para qualquer tipo de perfil -
aberto ou fechado - a equação anterior recebe mais um termo que
leva em conta esse efeito.
3
3
....
dx
d
IE
dx
d
IGM wtx


Este termo está associado não à Torção
de Saint Venant, mas à Torção de
Vlasov. É o termo associado à restrição
ao empenamento. O momento torçor que
é contante ao longo do comprimento tem
duas parcelas: Uma que é responsável
pelo Ângulo Unitário de torção e outra que
está associada à restrição a esse ângulo.

7
www.nce.com.br
TENSÕES NORMAIS NA FLEXO-TORÇÃO
si
w
ft
w
I
B
.
mBB  .2

    121 .... mxchCxshCB  
Da mesma forma que temos a Equação
Diferencial da Flexão, temos a Equação
Diferencial da Flexo-Torção, que exprime
as derivadas do Bimomento. Nessa
equação aparece o “Momento de Inércia à
sexta potência” ou a “ Warping
Constant”, representada por e a
coordenada Sectorial, ou Área Sectorial
representada por w.
w
I

8
www.nce.com.br

9
www.nce.com.br
desenvolvimento conceitual e analítico da analogia flexão-retorção
A teoria de Vlasov permite o equacionamento do problema de Flexo-Torção para
perfis abertos de paredes delgadas, por intermédio da Equação Diferencial do
Bimomento de Flexo-Torção. Vlasov encontrou a solução desta equação para
diversas condições de contorno e para vários casos de carregamentos aplicados a
uma viga isolada. Soluções Exatas tal como na teoria de flexão de vigas por
analogia.

10
www.nce.com.br
ALTERNATIVAS PARA DISCRETIZAÇÃO
Modelos convencionais com elementos de viga de 12 graus de liberdade não contabilizam a
flexo torção. Os elementos para isso deveriam considerar dois parâmetros a mais para
representar a flexo torção. Portanto 14 graus de liberdade.

11
www.nce.com.br
ANALOGIA FLEXÃO - RETORÇÃO

2
h
Z
h
z.2

3
3
....
dx
d
IE
dx
d
IGM wtx


3
3 .2
..
.2
..
dx
h
z
d
IE
dx
h
z
d
IGM wtx














3
3
...
2
...
2
dx
zd
IE
hdx
dz
IG
h
M wtx 
02

h
It
3
3
3
3
2
.*..
.2
.
dx
zd
IE
dx
zd
h
I
EF y
w
 3
3
..
dx
zd
IE
dx
dM
Q y
y
z 
*
2
.2
y
w
y I
h
I
I 
Uma alternativa desenvolvida para “enganar” o elementos de viga convencionais
mudando os parâmetros de entrada, levando em conta em alguns casos a rigidez
ao empenamento.

12
www.nce.com.br

13
www.nce.com.br
TESTES DE CONFIABILIDADE
VLASOV

14
www.nce.com.br
Método dos Elementos Finitos com Elementos de Casca
2
/00,410 cmKgf

15
www.nce.com.br
Analogia Flexão-Retorção
3847,40 Kgf.cm
3847,40 Kgf.cm
2
111
25,392863,8.
932,86
40,847.3
.
2
2
cm
kgf
ftwft d
I
M
 

16
www.nce.com.br
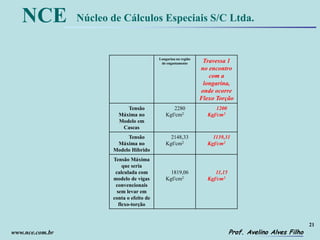
Tensões Normais de Flexo-Torção na Extremidade
Engastada da Viga -[ft] = kgf / cm2
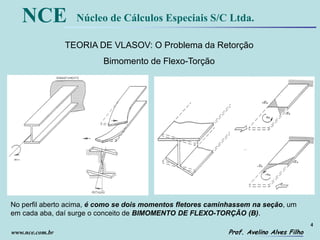
Teoria de
Vlasov
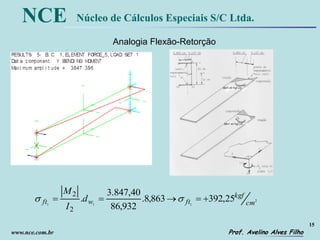
Analogia
Flexão-
Retorção
(MEF)
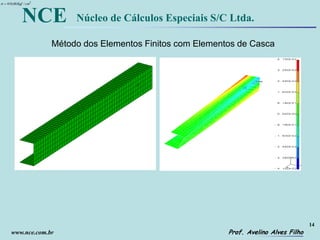
MEF com
Elementos de
Casca
Ponto 1 + 392,54 + 392,25 + 410,00
Ponto 6 - 271,81 - 271,60 - 275,36
Ponto 11 + 271,81 + 271,60 + 275,36
Ponto 16 - 392,54 - 392,25 - 410,00

17
www.nce.com.br
EXEMPLO DE APLICAÇÃO - CHASSI

18
www.nce.com.br
2
/2280 cmKgfZ  ./1200 2
cmKgfX 
ANÁLISE PELO MÉTODO DOS ELEMENTOS FINITOS
ELEMENTOS DE CASCA

19
www.nce.com.br
Análise pelo Método dos Elementos Finitos com "Modelo
Híbrido". Analogia Flexão-Retorção

20
www.nce.com.br

21
www.nce.com.br
Longarina na região
do engastamento Travessa 1
no encontro
com a
longarina,
onde ocorre
Flexo Torção
Tensão
Máxima no
Modelo em
Cascas
2280
Kgf/cm2
1200
Kgf/cm2
Tensão
Máxima no
Modelo Híbrido
2148,33
Kgf/cm2
1139,31
Kgf/cm2
Tensão Máxima
que seria
calculada com
modelo de vigas
convencionais
sem levar em
conta o efeito de
flexo-torção
1819,06
Kgf/cm2
11,15
Kgf/cm2

Sae 2004-a

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Sae 2004-a

Sae 2004-a