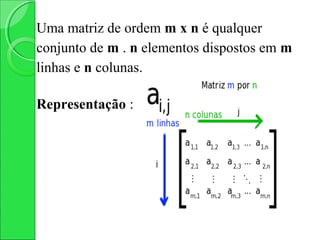
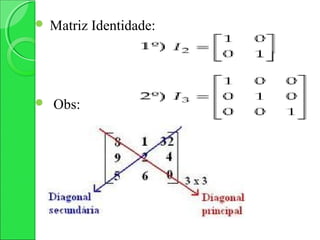
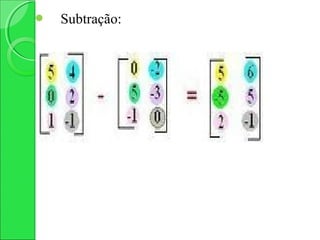
1) O documento discute matrizes, definindo-as como conjuntos de elementos dispostos em linhas e colunas. Classifica matrizes de acordo com o número de linhas e colunas e apresenta tipos como nula, diagonal e identidade. 2) Apresenta operações com matrizes como adição, subtração, produto por escalar e multiplicação. 3) Fornece exemplos numéricos de problemas envolvendo matrizes.

1. Matrizes
Marcela Monteiro

2. Uma matriz de ordem m x n é qualquer
conjunto de m . n elementos dispostos em m
linhas e n colunas.
Representação :

3. A = (aij)mxn | lei de formação.
Ex.: {(aij)2x3 | aij = i . j}

4. Classificação das Matrizes
Em função dos valores de m e n, classifica-se
a matriz A = (aij)mxn em:
m=1: matriz linha;
n=1 :matriz coluna;
matriz quadrada m=n:
matriz retangular m≠n

5. Tipos de Matrizes
 Matriz Nula:
 Matriz Diagonal:
 Matriz Transposta:

6.  Matriz Identidade:
 Obs:

7.  Matriz inversa : A · A-1 = A-1 · A = I

8. Operações com Matrizes
Adição:

9.  Subtração:

10.  Produto de uma Matriz por Escalar:

11.  Multiplicação de Matrizes:

12.  Obs:
1. (UFGO) Sejam as matrizes:
1 / 16 a2  2b 9
A=   e B = 3 
 − 27 log3 (1 / 81) a c
Para que elas sejam iguais, deve-se ter:
a)a= –3 e b= –c=4 b) a=3 e b=c=–4
c) a=3 e b= –c=4 d)a= –3 e b=c= –4.
e) a= –3 e b=c2= 4

13. 2.(UFRN) A solução da equação matricial
é um número:
 − 1 2   x + 1 x + 4
 x x 2 − 2 =  3 x + 4 2 
   
a)maior que –1 b)menor que –1. c)maior que 1
d)entre –1 e 1 e)entre 0 e 3
3. (FGV-SP) Dadas as matrizes x y  x 6  4 x + y
A=   B =  − 1 2 w C =  z + w 3 
e sendo 3A= B + C, então: z w    
a)x + y + z + w=11 b) x + y + z + w=10.
c) x + y – z – w =0 d) x + y – z – w = –1
e) x + y + z + w>11

14. 4.(PUC-SP) Se
A = [ 25 12 13] , B = [ 5 − 8 3] e C = [ − 1 10 − 1]
então a matriz X, tal que A + B – C – X = 0
é:
a)[31 –6 17] b)[17 –6 31]
c)[–31 –6 –17] d)[31 6 17]
e)[17 6 31]

15. ANEXO
 Porcentagem:Toda a razão que tem para
consequente o número 100 denomina-se
razão centesimal.
Alguns exemplos:
a) 7/ 100= 0,07 = 7%
b) 16/ 100= 0,16 = 16%
Obs: 16% e 7% são chamadas taxas
centesimais ou taxas percentuais.

16. João vendeu 50% dos seus 50 cavalos.
Quantos cavalos ele vendeu?
50% de 50= 50/ 100 . 50 = 25
Para solucionar esse problema devemos
aplicar a taxa percentual (50%) sobre o
total de cavalos.
Logo, ele vendeu 25 cavalos, que representa
a porcentagem procurada.Portanto, chegamos a
seguinte definição:
Porcentagem é o valor obtido ao aplicarmos uma
taxa percentual a um determinado valor.

17. Exemplos:
a) Calcular 10% de 300.
b) Calcular 25% de 200kg.
c) Um jogador de futebol, ao longo de um
campeonato, cobrou 75 faltas,
transformando em gols 8% dessas faltas.
Quantos gols de falta esse jogador fez?

18. (COVEST) Uma revista semanal de larga circulação
apresentou matéria contendo o seguinte texto: “O
governo destinou 400.000 reais para a vacinação de 25
milhões de cabeças de gado, ou seja, um centavo de
real para cada cabeça”. De qual percentual a revista
errou, acerca do valor que o governo destinou a cada
cabeça de gado?

19. A nossa maior glória não reside no fato de
nunca
cairmos, mas sim em levantarmo-nos sempre
depois de cada queda.
(Confúcio)