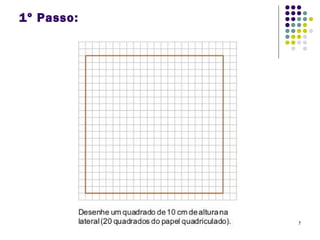
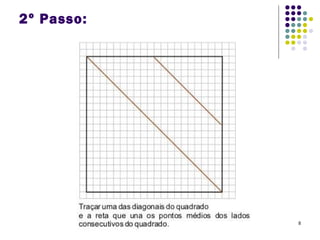
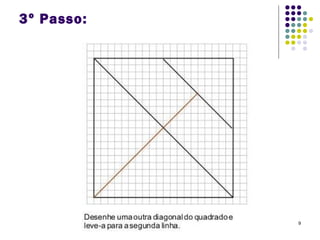
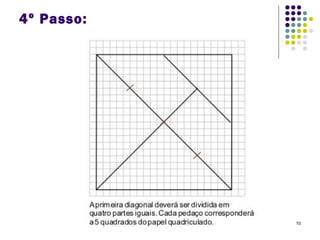
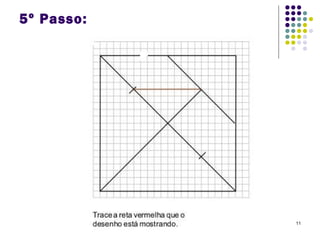
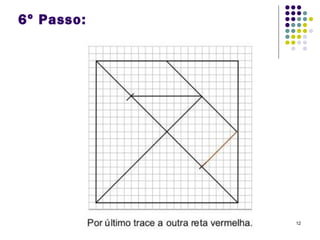
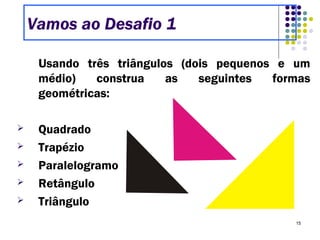
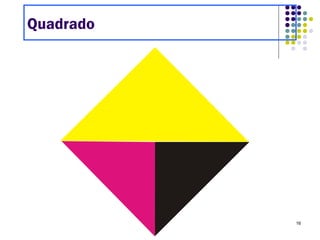
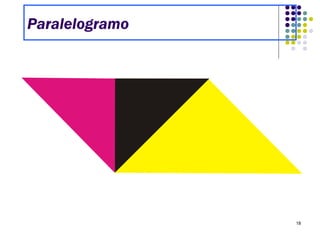
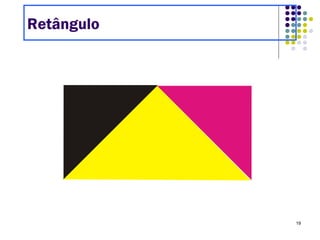
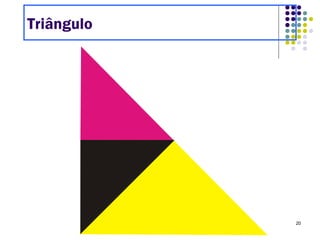
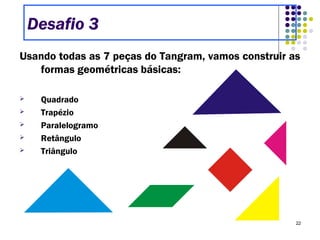
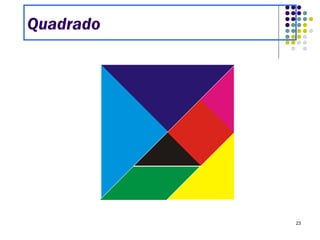
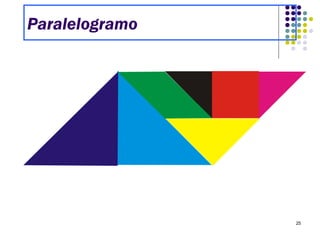
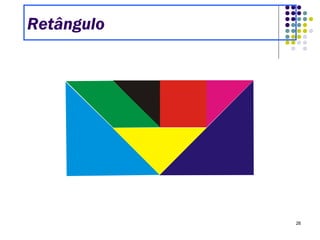
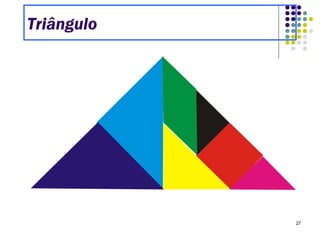
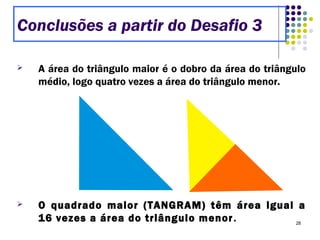
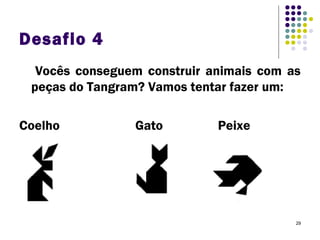
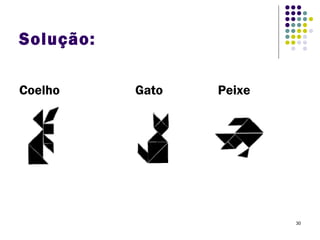
O Tangram é um quebra-cabeça chinês feito de 7 peças que podem ser usadas para formar várias figuras geométricas e imagens. Embora sua origem exata seja desconhecida, sabe-se que chegou à Europa e Estados Unidos no século XIX. O documento ensina como construir figuras usando as peças do Tangram e apresenta desafios para os alunos praticarem.