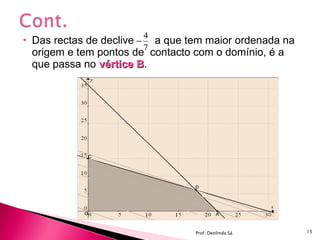
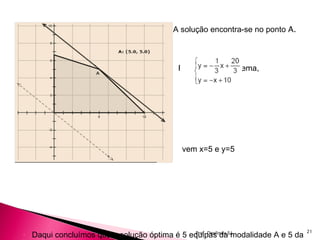
A programação linear é uma técnica de otimização que usa expressões lineares para modelar problemas e encontrar soluções ótimas. Ela surgiu em 1947 para resolver problemas logísticos durante a Segunda Guerra Mundial. Problemas de programação linear definem variáveis de decisão, uma função objetivo a ser otimizada e restrições a serem satisfeitas.

1. Breve Introdução Prof. Deolinda Sá

2. A Programação Linear é uma técnica de optimização bastante utilizada na resolução de problemas cujos modelos matemáticos são representados por expressões lineares. A programação Linear é um ramo muito jovem da matemática que surgiu em 1947, quando George B. Dantzig inventou e desenvolveu o “Método Simplex” para resolver problemas de optimização formulados a partir de questões de logística da Força Aérea dos E.U.A., durante a segunda Guerra Mundial. Prof. Deolinda Sá

3. A palavra “ Programação ” refere-se a uma programação de tarefas ou planificação , não a uma programação no sentido da informática. A palavra “ Linear ” , advém do facto das expressões (condições) que se utilizam serem lineares. Prof. Deolinda Sá

4. São problemas que procuram o óptimo. O óptimo na globalidade é um mínimo ou um máximo a ser alcançado, nas condições existentes. Nos problemas de Programação Linear algumas decisões têm de ser tomadas. Estas decisões são representadas pelas variáveis de decisão x e y, utilizadas no modelo de programação linear. A estrutura base de um problema de programação linear é maximizar ou minimizar a função objectivo que satisfaz a um conjunto de restrições ou condições. Geometricamente, as restrições lineares definem um polígono convexo, chamado de conjunto de pontos admissíveis ou região admissível . Prof. Deolinda Sá

5. As restrições ou condições utilizadas em programação linear são representadas por equações ou inequações. Resumindo Para formular um problema de Programação Linear deve-se: Definir as variáveis de decisão (o que pretendemos determinar) Definir a função objectivo (o que se pretende optimizar) Estabelecer as restrições (as condições que têm que ser satisfeitas) Prof. Deolinda Sá

6. Uma empresa fabrica dois produtos A e B . Cada um destes produtos requer uma certa quantidade de tempo na linha de montagem e ainda mais algum para a sua finalização. Cada produto do tipo A necessita de 5 horas na linha de montagem e de 2 horas para a finalização. Cada produto de tipo B necessita de 3 horas na linha de montagem e de 4 horas para a finalização. Numa semana, a empresa dispõe de 108 horas para a linha de montagem e 60 horas para a finalização. Toda a produção é vendida. O lucro de cada produto é de 120 € para o produto A e de 210 € para o B . Prof. Deolinda Sá

7. Quantas unidades, por semana, dos produtos A e B se devem produzir, de modo a que o lucro seja máximo? Podemos elaborar uma tabela para melhor organizar os dados: Prof. Deolinda Sá Montagem Finalização Lucro A 5 2 120 B 3 4 210 Disponibilidade 108 60

8. Seja x o número de unidades que a empresa produz, por semana, do produto A . y o número de unidades que a empresa produz, por semana, do produto B. O tempo necessário na linha de montagem para os dois produtos é 5x+3y horas, no total. Como somente existem 108 horas de disponibilidade, temos a restrição: 5x+3y ≤ 108 De forma análoga temos a seguinte restrição: 2x+4y ≤ 60 Prof. Deolinda Sá

9. Cada unidade do produto A origina um lucro de 120 euros. Assim, com x unidades produzidas do produto A , obtêm-se 120x euros de lucro. Cada unidade do produto B origina um lucro de 210 euros. Assim, com y unidades de B , obtêm-se 210y euros de lucro. O lucro semanal é dado por: L= 120x+210y . Temos ainda as condições x ≥ 0 e y ≥ 0, pois a produção é não negativa Pretendemos maximizar o lucro. Prof. Deolinda Sá

10. Variáveis de decisão (o que pretendemos determinar): x e y ( número de unidades ) Função Objectivo (o que se pretende optimizar) maximizar o lucro: L= 120x+210y Restrições (condições que têm de ser satisfeitas) Prof. Deolinda Sá

11. Como x ≥ 0 e y ≥ 0 , iremos precisar somente do primeiro quadrante. As outras duas restrições resolvem-se em ordem a y e considera-se o domínio plano respectivo. Prof. Deolinda Sá

12. A solução que procuramos encontra-se no polígono [OABC] . Prof. Deolinda Sá

13. Os pontos que estão nesta região dizem-se pontos admissíveis . E os vértices O, A, B e C dizem-se vértices da região admissível. Que pontos maximizam o lucro? A expressão representa uma família de rectas todas com o declive e cuja ordenada na origem é . Prof. Deolinda Sá

14. Assim sendo, um maior valor de corresponde a um maior valor de L . Logo, a resolução do nosso problema consiste em encontrar a recta com declive de maior ordenada na origem e que tenha algum contacto com o polígono. Prof. Deolinda Sá

15. Das rectas de declive a que tem maior ordenada na origem e tem pontos de contacto com o domínio, é a que passa no vértice B . Prof. Deolinda Sá

16. As coordenadas do ponto B determinam-se resolvendo o sistema A solução do sistema é o par (18,6), logo as coordenadas do ponto B. Assim para que a empresa, que produz o produtos A e B, tenha o maior lucro possível, deve produzir semanalmente 18 unidades do produto A e 6 unidades do produto B. Esse lucro será: L= 120  18 + 210  6 = 3420 euros semanais. Prof. Deolinda Sá

17. Se tivermos presente o seguinte teorema : Dado um problema de programação linear, se R for a região admissível e for limitada, então existe um máximo e um mínimo em R e cada um destes ocorre pelo menos num dos vértices da região. Se R não for limitada, então pode não existir nem máximo nem mínimo. Mas se existir ele encontra-se num vértice de R. Ficamos a saber que a solução que procuramos encontra-se num dos vértices da área admissível. Observemos a tabela ao lado. Facilmente identificamos a solução óptima (18,6) . Prof. Deolinda Sá x y L=120x+210y O 0 0 0 A 21,6 0 2592 B 18 6 3420 C 0 15 3150

18. Numa turma do 11º ano há 30 jovens: 20 raparigas e 10 rapazes A turma vai participar num concurso que admite duas modalidades de equipas: Modalidade A : Equipas de 2 elementos, um de cada sexo. Prémio de participação: 50€ Modalidade B : Equipas de 4 elementos, três raparigas e um rapaz. Prémio de participação: 60€. Quantas equipas de cada tipo se devem constituir para a turma receber o valor máximo em prémios de participação, sabendo que cada um dos alunos não pode participar em mais do que uma equipa? Prof. Deolinda Sá

19. Comecemos por escolher as variáveis : x – n.º de equipas da modalidade A y – n.º de equipas da modalidade B Vejamos quais são as restrições : x≥0 y≥0 , semiplano definido pela recta que passa nos pontos (2,6) e (5,5) , semiplano definido pela recta que passa nos pontos (0,10) e (10,0) Prof. Deolinda Sá

20. A função objectivo é: Resolvendo em ordem a y temos: Assim, temos uma família de rectas paralelas de declive A representação da região admissível e da recta que traduz a família da função objectivo é a seguinte: Prof. Deolinda Sá

21. A solução encontra-se no ponto A. Resolvendo o sistema, vem x=5 e y=5 Daqui concluímos que a solução óptima é 5 equipas da modalidade A e 5 da modalidade B. A esta solução corresponde um prémio de participação de 50  5+ 60  5=550€ Prof. Deolinda Sá