Logica computacional

Lógica Computacional
Diego Silveira Costa Nascimento
Instituto Federal do Rio Grande do Norte
diego.nascimento@ifrn.edu.br
28 de maio de 2014

Ementa do Curso
1 Introdução
2 Lógica Proposicional
3 Construção de Tabelas-verdade
4 Tautologia, Contradição e Contingência
5 Implicação Lógica
6 Equivalência Lógica
7 Álgebra das Proposições e Método Dedutivo
8 Inferência Lógica
9 Demonstração Indireta
10 Sentenças Abertas
11 Quantiﬁcadores
Diego S. C. Nascimento (IFRN) Lógica Computacional Apresentação 2 / 121

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Objetivos da Disciplina
Apresentar a disciplina de Lógica;
Discutir o cenário no qual a disciplina poderá ser aplicada;
Apresentar um pouco da história da lógica;
Fazer com que o estudante consiga no futuro relacionar os aspectos
abstratos da computação com sua implementação; e
Incentivar a escrita dos algoritmos antes de sua implementação
propriamente dita.

Motivações em Estudar Lógica
O estudo desta disciplina faz o aluno adquirir ou aperfeiçoar seu raciocínio
lógico no intuito de desenvolverem programas e sistemas em uma
determinada linguagem de programação.
A Lógica é apresentada como uma técnica eﬁciente para:
a organização de conhecimentos em qualquer área;
raciocinar corretamente sem esforço consciente;
interpretar e analisar informações rapidamente;
aumentar a competência linguística (oral e escrita);
adquirir destreza com o raciocínio quantitativo; e
detectar padrões em estruturas (premissas, pressuposições, cenários,
etc.)

Lógica
A palavra Lógica deriva do Grego (logos), que signiﬁca: palavra,
pensamento, ideia, argumento, relato, razão lógica ou princípio lógico.
Deﬁnição
Lógica é a ciência das leis ideais do pensamento e a arte de aplicá-las à
pesquisa e à demonstração da verdade.

Origem da Lógica
A Lógica teve início na Grécia em 342 a.C.;
Aristóteles sistematizou os conhecimentos existentes em Lógica,
elevando-a à categoria de ciência;
Em sua obra chamada Organum (“ferramenta para o correto pensar”),
estabeleceu princípios tão gerais e tão sólidos que até hoje são
considerados válidos.
Aristóteles se preocupava com as formas de raciocínio que, a partir de
conhecimentos considerados verdadeiros, permitiam obter novos
conhecimentos; e
A partir dos conhecimentos tidos como verdadeiros, caberia à Lógica a
formulação de leis gerais de encadeamentos lógicos que levariam à
descoberta de novas verdades.

Argumento Lógico
Em Lógica, o encadeamento de conceitos é chamado de argumento;
As aﬁrmações de um argumento são chamadas de proposições;
Um argumento é um conjunto de proposições tal que se aﬁrme que
uma delas é derivada das demais;
Usualmente, a proposição derivada é chamada de conclusão, e as
demais, de premissas; e
Em um argumento válido, as premissas são consideradas provas
evidentes da verdade da conclusão.

Exemplo de Argumento

Inferência Lógica
Lógica dispõe de duas ferramentas principais que podem ser utilizadas pelo
pensamento na busca de novos conhecimentos: a dedução e a indução.
Dedução
Um argumento dedutivo é válido quando suas premissas, se
verdadeiras, fornecem provas convincentes para sua conclusão; e
De forma geral, a dedução sempre preserva a verdade.
Indução
Um argumento indutivo fornece provas cabais da veracidade da
conclusão, ou seja, apenas que forne indicações dessa veracidade; e
De forma geral, a indução nem sempre preserva a verdade.

Exemplos de Inferências Dedutiva e Indutiva
Em outras palavras, na dedução, a conclusão é consequência necessária das
premissas, e na indução, a conclusão é consequência plausível das
premissas.

Princípios Lógicos
A Lógica Formal repousa sobre três princípios fundamentais que permitem
todo seu desenvolvimento posterior, e que dão validade a todos os atos do
pensamento e do raciocínio. São eles:
Princípio da Identidade
Aﬁrma A = A e não pode ser B, o que é, é;
Princípio da Não Contradição
A = A e nunca pode ser não-A, o que é, é e não pode ser sua
negação, ou seja, o ser é, o não ser não é; e
Princípio do Terceiro Excluído
Aﬁrma que Ou A é x ou A é y, não existe uma terceira possibilidade.

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Logica Proposicional
Definição
É um sistema formal no qual as fórmulas representam proposições que
podem ser formadas pela combinação de proposições atômicas usando
conectivos lógicos e um sistema de regras de derivação, que permite que
certas fórmulas sejam estabelecidas como “teoremas” do sistema formal.
Em termos gerais, um cálculo proposicional é frequentemente apresentado
como um sistema formal que consiste em um conjunto de expressões
sintáticas (fórmulas bem formadas, ou fbfs), um subconjunto distinto
dessas expressões, e um conjunto de regras formais que define uma relação
binária específica, que se pretende interpretar como a noção de equivalência
lógica, no espaço das expressões.

Proposições
Chama-se proposição todo o conjunto de palavras ou símbolos que
exprimem um pensamento de sentido completo;
As proposições transmitem pensamentos; e
Aﬁrmam fatos ou exprimem juízos que formamos a respeito de
determinados entes.
Exemplos
A Lua é um satélite da Terra;
Sócrates é um homem;
Eu estudo Lógica;
Todos os homens são mortais; ou
Não existe homem inﬁel.

A Linguagem da Lógica Proposicional
Considere o conjunto de símbolos:
A = {(, ), ¬, ∧, ∨, →, ↔, p, q, r, s, . . .}
A esse conjunto é chamado de alfabeto da Lógica Proposicional;
As letras são símbolos não lógico (letras sentenciais); e
O restante são símbolos lógicos (parênteses e conectivos lógicos);

Letras Sentenciais
As letras sentenciais são usadas para representar proposições elementares
ou atômicas, isto é, proposições que não possuem partes que sejam
também proposições.
Exemplos
p = O céu é azul;
Q = Eu estudo lógica;
r = 2 + 2 = 4; ou
s = Sócrates é um homem.
Importante
As partes dessas proposições não são proposições mais simples, mas sim,
componentes subsentenciais: expressões, palavras, sílabas ou letras.

Conectivos Lógicos
As proposições compostas são obtidas combinando proposições
simples através de certos termos chamados conectivos;
A Lógica dispõe de cinco tipos de conectivos e seus operadores:
Não (Negação), ¬ ;
E (Conjunção), ∧;
Ou (Disjunção), ∨;
Se – então (Condicional), →;e
Se e somente se (Bicondicional), ↔.
Exemplos
Não está chovendo;
Está chovendo e está ventando;
Está chovendo ou está nublado;
Se choveu, então está molhado; ou
Será aprovado se e somente se estudar.

Operador de Negação: ¬
A característica peculiar da negação, tal como ela se apresenta na lógica
proposicional clássica, é que toda proposição submetida à operação de
negação resulta na sua contraditória.
Exemplo
p = Está chovendo.
Ler-se ¬p, como: “Não está chovendo.”
Importante
O fato expresso por uma proposição não pode ocorrer ao mesmo tempo e
sob o mesmo modo e circunstância que o fato expresso pela negação dessa
mesma proposição.

Tabela Verdade: ¬
Se p é uma proposição, a expressão ¬p é chamada negação de p; e
Claramente, a negação inverte o valor verdade de uma expressão.
Exemplo
p ¬p
V F
F V

Operador de Conjunção: ∧
A característica peculiar da conjunção está no fato de fórmulas conjuntivas
expressarem a concomitância de fatos. A fórmula (p ∧ q) expressa que o
fato expresso por p ocorre ao mesmo tempo que o fato expresso por q.
Exemplo
p = Está chovendo.
q = Está ventando.
Ler-se p ∧ q, como: “Está chovendo e está ventando.”

Tabela Verdade: ∧
Se p e q são proposições, a expressão p ∧ q é chamada conjunção de p
e q; e
As proposições p e q são chamadas fatores da expressão.
Exemplo
p q p∧q
V V V
V F F
F V F
F F F

Operador de Disjunção: ∨
A característica peculiar da disjunção consiste no fato de proposições
disjuntivas expressarem que pelo menos um de dois fatos ocorre. A fórmula
(p ∨ q) expressa que, dentre os fatos expressos por p e q respectivamente,
pelo menos um deles ocorre.
Exemplo
p = Está nublado.
q = Está chovendo.
Ler-se p ∨ q, como: “Está nublado ou está chovendo.”

Tabela Verdade: ∨
Se p e q são proposições, a expressão p ∨ q é chamada disjunção
inclusiva de p e q; e
As proposições p e q são chamadas parcelas da expressão.
Exemplo
p q p∨q
V V V
V F V
F V V
F F F

Operador Condicional: →
A característica peculiar dessa operação consiste em que um condicional
(p → q) expressa que a ocorrência do fato expresso por p garante
necessariamente a ocorrência do fato expresso por q.
Exemplo
p = Choveu.
q = Está molhado.
Ler-se p → q, como: “Se choveu, então está molhado.”

Tabela Verdade: →
Se p e q são proposições, a expressão p → q é chamada condicional
de p e q;
A proposição p é chamada antecedente, e a proposição q consequente
da condicional; e
A operação de condicionamento indica que o acontecimento de p é
uma condição para que q aconteça.
Exemplo
p q p→q
V V V
V F F
F V V
F F V

Operador Bicondicional: ↔
A característica peculiar dessa operação consiste em que um bicondicional
(p ↔ q) assevera que os fatos expressos por p e q são interdependentes,
isto é, ou os dois ocorrem juntos ou nenhum dos dois ocorrem.
Exemplo
p = Será aprovado.
q = Estudar.
Ler-se p ↔ q, como: “ Será aprovado, se e somente se estudar.”

Tabela Verdade: ↔
Se p e q são proposições, a expressão p ↔ q é chamada bicondicional
de p e q; e
A operação de bicondicionamento indica que p é uma condição para
que q aconteça, e vice-versa.
Exemplo
p q p↔q
V V V
V F F
F V F
F F V

Parênteses: (e)
A necessidade de usar parênteses na simbolização das proposições se deve
ao fato de se evitar qualquer tipo de ambiguidade.
Exemplo
p = Estudar.
q = Fazer a prova.
r = Fazer o trabalho.
s = Serei aprovado.
Ler-se ((p ∧ q) ∨ r) → s, como:
“ Se ((estudar e fazer a prova) ou fazer o trabalho), então será aprovado.”

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Tabela-verdade de uma Proposição Composta
Dadas várias proposições simples p, q, r, . . ., podemos combiná-las pelos
operadores lógicos ∧, ∨, →, ↔ e construir proposições compostas:
Exemplo
P(p, q) = ¬p ∨ (p → q)
Q(p, q) = (p ↔ ¬q) ∧ q
R(p, q, r) = (p → ¬q ∨ r) ∧ ¬(q ∨ (p ↔ ¬r))
Então, com o emprego das tabelas-verdade das operações lógicas
fundamentais já estudadas: ¬p, p ∧ q, p ∨ q, p → q e p ↔ q;
É possível construir a tabela-verdade correspondente a qualquer
proposição composta; e
A tabela-verdade exibirá exatamente os casos em que a proposição
composta será verdadeira (V ) ou falsa (F), admitindo-se que o seu
valor lógico só depende dos valores lógicos das proposições simples.

Ordem de Precedência dos Operadores
1 Percorra a expressão da esquerda para a direita, executando as
operações de negação, na ordem em que aparecerem;
2 Percorra novamente a expressão, da esquerda para a direita,
executando as operações de conjunção e disjunção, na ordem em que
aparecerem;
3 Percorra outra vez a expressão, da esquerda para a direita, executando
desta vez as operações de condicionamento, na ordem em que
aparecerem; e
4 Percorra uma última vez a expressão, da esquerda para a direita,
executando as operações de bicondicionamento, na ordem em que
aparecerem.

Construindo a Tabela-verdade
Dada uma expressão proposicional composta, e dados os valores lógicos das
proposições simples que a compõe, podemos, com a ordem de precedência,
calcular o valor lógico da expressão dada.
Expressão Proposicional Composta
P(p, q) = ¬(p ∧ ¬q)
Forma-se, em primeiro lugar, o par de colunas correspondentes às duas
proposições simples p e q.
Exemplo
p q
V V
V F
F V
F F

Construindo a Tabela-verdade (cont.)
Em seguida, forma-se a coluna para ¬q.
Exemplo
p q ¬q
V V F
V F V
F V F
F F V

Depois, forma-se a coluna para p ∧ ¬q.
Exemplo
p q ¬q p∧¬q
V V F F
V F V V
F V F F
F F V F

Por ﬁm, forma-se a coluna relativa aos valores lógicos da proposição
composta ¬(p ∧ ¬q).
Exemplo
p q ¬q p∧¬q ¬(p∧¬q)
V V F F V
V F V V F
F V F F V
F F V F V

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Tautologia
Deﬁnição
Tautologia é toda proposição composta P(p, q, r, . . .) cujo valor lógico é
sempre verdadeiro, quaisquer que sejam os valores lógicos das proposições
simples p, q, r, . . .
As tautologias são também denominadas proposições tautológicas ou
proposições logicamente verdadeiras.

Tautologia: Demonstração I
Proposição
¬(p ∧ ¬p)
Exemplo
p ¬p p∧¬p ¬( p∧¬p)
V F F V
F V F V
Portanto, dizer que uma proposição não pode ser simultaneamente
verdadeira e falsa é sempre verdadeiro.

Tautologia: Demonstração II
Proposição
p ∨ ¬p
Exemplo
p ¬p p∨¬p
V F V
F V V
Portanto, dizer que uma proposição ou é verdadeira ou é falsa é sempre
verdadeiro.

Contradição
Deﬁnição
Contradição é toda proposição composta P(p, q, r, . . .) cujo valor lógico é
sempre falso, quais quer que sejam os valores lógicos das proposições
simples p, q, r, . . .
As contradições são também denominadas proposições contraválidas ou
proposições logicamente falsas.

Contradição: Demonstração I
Proposição
p ∧ ¬p
Exemplo
p ¬p p∧¬p
V F F
F V F
Portanto, dizer que uma proposição pode ser simultaneamente verdadeira e
falsa é sempre falso.

Contradição: Demonstração II
Proposição
p ↔ ¬p
Exemplo
p ¬p p↔ ¬p
V F F
F V F

Contingência
Deﬁnição
Contingencia é toda a proposição composta que não é tautologia nem
contradição.
As contingências são também denominadas proposições contingentes ou
proposições indeterminadas.

Contingência: Demonstração I
Proposição
p → ¬p
Exemplo
p ¬p p→ ¬p
V F F
F V V

Contingência: Demonstração II
Proposição
p ∨ q → p
Exemplo
p q p∨q p∨q → p
V V V V
V F V V
F V V F
F F F V

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Implicação Lógica
Deﬁnição
Diz-se que uma proposição P(p, q, r, . . .) implica logicamente uma
proposição Q(p, q, r, . . .), se Q(p, q, r, . . .) é verdadeiro todas as vezes em
que P(p, q, r, . . .) é verdadeiro.
Notação
P(p, q, r, . . .) ⇒ Q(p, q, r, . . .)
Importante
Em particular, toda proposição implica uma tautologia e somente uma
contradição implica uma contradição.

Propriedades da Implicação Lógica
É imediato que a relação de implicação lógica entre proposições utiliza-se
das propriedades reﬂexiva (R) e transitiva (T).
Exemplo
(R) P(p, q, r, . . .) ⇒ P(p, q, r, . . .)
(T) Se P(p, q, r, . . .) ⇒ Q(p, q, r, . . .) e
Q(p, q, r, . . .) ⇒ R(p, q, r, . . .), então
P(p, q, r, . . .) ⇒ R(p, q, r, . . .)

Demonstração de Implicação Lógica I
Proposições
p ∧ q, p ∨ q e p ↔ q
Exemplo
p q p∧q p∨q p↔q
V V V V V
V F F V F
F V F V F
F F F F V
A proposição p ∧ q é verdadeira somente na linha 1, e nesta linha, as
proposições p ∨ q e p ↔ q também são verdadeiras. Logo, a primeira
proposição implica cada uma das outras duas proposições, isto é:
p ∧ q ⇒ p ∨ q e p ∧ q ⇒ p ↔ q

Demonstração de Implicação Lógica II
Proposições
p ↔ q, p → q e q → p
Exemplo
p q p↔q p→q q→p
V V V V V
V F F F V
F V F V F
F F V V V
A proposição p ↔ q é verdadeira nas linhas 1 e 4 e, nestas linhas,
proposições p → q e q → p também são verdadeiras. Logo, a primeira
proposição implica cada uma das outras duas proposições, isto é:
p ↔ q ⇒ p → q e p ↔ q ⇒ q → p

Tautologias e Implicação Lógica
Teorema
A proposição P(p, q, r, . . .) implica a proposição Q(p, q, r, . . .) isto é:
P(p, q, r, . . .) ⇒ Q(p, q, r, . . .)
se e somente se a condicional:
P(p, q, r, . . .) → Q(p, q, r, . . .)
é tautológica.
Importante
Os símbolos → e ⇒ são distintos, pois o primeiro é de operação lógica
(aplicado, por ex., às proposições p e q dá a nova proposição p → q),
enquanto que o segundo é de relação (estabelece que a condicional
P(p, q, r, . . .) → Q(p, q, r, . . .) é tautológica).

Demonstração de Tautologia e Implicação Lógica
Condicional
(p → q) ∧ p → q
Exemplo
p q p→q (p→q)∧ p (p→q)∧ p → q
V V V V V
V F F F V
F V F F V
F F V F V
Portanto, simbolicamente: (p → q) ∧ p ⇒ q

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Equivalência Lógica
Deﬁnição
Diz-se que uma proposição P(p, q, r, . . .) é logicamente equivalente a uma
proposição Q(p, q, r, . . .), se as tabelas-verdade destas duas proposições
são idênticas.
Notação
P(p, q, r, . . .) ⇔ Q(p, q, r, . . .)
Importante
Em particular, se as proposições P(p, q, r, . . .) e Q(p, q, r, . . .) são ambas
tautológicas ou são ambas contradições, então são equivalentes.

Propriedades da Equivalência Lógica
É imediato que a relação de equivalência lógica entre proposições utiliza-se
das propriedades reﬂexiva(R), simétrica (S) e transitiva (T), isto é,
simbolicamente:
Exemplo
(R) P(p, q, r, . . .) ⇔ P(p, q, r, . . .)
(S) Se P(p, q, r, . . .) ⇔ Q(p, q, r, . . .), então
Q(p, q, r, . . .) ⇔ P(p, q, r, . . .)
(T) Se P(p, q, r, . . .) ⇔ Q(p, q, r, . . .) e
Q(p, q, r, . . .) ⇔ R(p, q, r, . . .), então
P(p, q, r, . . .) ⇔ R(p, q, r, . . .)

Demonstração de Equivalência Lógica I
Proposições
¬p → p e p
Exemplo
p ¬p ¬p→p
V F V
F V F
A proposição ¬p → p e p são equivalentes nas colunas 1 e 2, isto é:
¬p → p ⇔ p

Demonstração de Equivalência Lógica II
Proposições
p → p ∧ q e p → q
Exemplo
p q p∧q p→p∧q p→q
V V V V V
V F F F F
F V F V V
F F F V V
A proposição p → p ∧ q e p → q são equivalentes nas colunas 4 e 5, isto é:
p → p ∧ q ⇔ p → q

Tautologias e Equivalência Lógica
Teorema
A proposição P(p, q, r, . . .) é equivalente à proposição Q(p, q, r, . . .), isto é:
P(p, q, r, . . .) ⇔ Q(p, q, r, . . .)
se e somente se a bicondicional:
P(p, q, r, . . .) ↔ Q(p, q, r, . . .)
é tautológica.
Importante
Os símbolos ↔ e ⇔ são distintos, pois o primeiro é de operação lógica
(aplicado, por ex., às proposições p e q dá a nova proposição p ↔ q),
enquanto que o segundo é de relação (estabelece que a bicondicional
P(p, q, r, . . .) ⇔ Q(p, q, r, . . .) é tautológica).

Demonstração de Equivalência Lógica
Proposições
(p ∧ ¬q → c) e (p → q)
Exemplo
p q c p∧¬q p∧¬q→c p→q (p∧¬q→c) ↔ (p→q)
V V F F V V V
V F F V F F V
F V F F V V V
F F F F V V V
...
...
...
...
...
...
...

Proposições Associadas a uma Condicional
Deﬁnição
Dada a condicional p → q, chama-se proposição associada a p → q as três
proposições condicionais que contêm p e q:
1 Proposição recíproca de p → q é q → p;
2 Proposição contrária de p → q é ¬p → ¬q; e
3 Proposição contrapositiva de p → q é ¬q → ¬p.
Exemplo
p q p→q q→p ¬p→ ¬q ¬q→ ¬p
V V V V V V
V F F V V F
F V V F F V
F F V V V V

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Propriedades da Conjunção
Seja p, q e r proposições simples quaisquer e sejam t e c proposições
também simples cujos valores lógicos respectivos são verdadeiro e falso,
temos as propriedades a seguir: idempotente, comutativa, associativa e
identidade.
Idempotente
p ∧ p ⇔ p
Exemplo
p p∧p p∧p↔p
V V V
F F V

Propriedades da Conjunção (cont.)
Comutativa
p ∧ q ⇔ q ∧ p
Exemplo
p q p∧q q∧p p∧q↔q∧p
V V V V V
V F F F V
F V F F V
F F F F V

Associativa
(p ∧ q) ∧ r ⇔ p ∧ (q ∧ r)
Exemplo
p q r p∧q (p∧q)∧r q∧r p∧(q∧r)
V V V V V V V
V V F V F F F
V F V F F F F
V F F F F F F
F V V F F V F
F V F F F F F
F F V F F F F
F F F F F F F

Identidade
p ∧ t ⇔ p e p ∧ c ⇔ c
Exemplo
p t c p∧t p∧c p∧t↔p p∧c↔c
V V F V F V V
F V F F F V V

Propriedades da Disjunção
Seja p, q e r proposições simples quaisquer e sejam t e c proposições
também simples cujos valores lógicos respectivos são verdadeiro e falso,
temos as propriedades a seguir: idempotente, comutativa, associativa e
identidade.
Idempotente
p ∨ p ⇔ p
Exemplo
p p∨p p∨p↔p
V V V
F F V

Propriedades da Disjunção (cont.)
Comutativa
p ∨ q ⇔ q ∨ p
Exemplo
p q p∨q q∨p p∨q↔q∨p
V V V V V
V F V V V
F V V V V
F F F F V

Associativa
(p ∨ q) ∨ r ⇔ p ∨ (q ∨ r)
Exemplo
p q r p∨q (p∨q)∨r q∨r p∨(q∨r)
V V V V V V V
V V F V V V V
V F V V V V V
V F F V V F V
F V V V V V V
F V F V V V V
F F V F V V V
F F F F F F F

Identidade
p ∨ t ⇔ t e p ∨ c ⇔ p
Exemplo
p t c p∨t p∨c p∨t↔t p∨c↔p
V V F V V V V
F V F V F V V

Propriedades da Conjunção e Disjunção
Seja p, q e r proposições simples quaisquer, podemos representar as
propriedades: distributiva, absorção e regras De Morgan.
Distributiva
p ∧ (q ∨ r) ⇔ (p ∧ q) ∨ (p ∧ r) e p ∨ (q ∧ r) ⇔ (p ∨ q) ∧ (p ∨ r)
Exemplo
p q r q∨r p∧(q∨r) p∧q p∧r (p∧q) ∨ (p∧r)
V V V V V V V V
V V F V V V F V
V F V V V F V V
V F F F F F F F
F V V V F F F F
F V F V F F F F
F F V V F F F F
F F F F F F F F

Propriedades da Conjunção e Disjunção (cont.)
Absorção
p ∧ (p ∨ q) ⇔ p e p ∨ (p ∧ q) ⇔ p
Exemplo
p q p∨q p∧(p∨q) p∧(p∨q) ↔p
V V V V V
V F V V V
F V V F V
F F F F V

Propriedades da Conjunção e Disjunção (cont.)
Regras De Morgan (1806–1871)
¬(p ∧ q) ⇔ ¬p ∨ ¬q e ¬(p ∨ q) ⇔ ¬p ∧ ¬q
Exemplo
p q p∧q ¬(p∧q) ¬p ¬q ¬p∨¬q
V V V F F F F
V F F V F V V
F V F V V F V
F F F V V V V

Negação da Condicional
Demonstração
Como p → q ⇔ p ∧ ¬q, temos:
¬(p → q) ⇔ ¬(¬p ∨ q) ⇔ ¬¬p ∧ ¬q
ou seja:
¬(p → q) ⇔ p ∧ ¬q
Exemplo
p q p→q ¬(p→q) ¬q p∧¬p
V V V F F F
V F F V V V
F V V F F F
F F V F V F

Negação da Bicondicional
Demonstração
Como p ↔ q ⇔ (p → q) ∧ (q → p), temos:
p ↔ q ⇔ (¬p ∨ q) ∧ (¬q ∨ p)
e portanto:
¬(p ↔ q) ⇔ ¬(¬p ∨ q) ∨ ¬(¬q ∨ p) ⇔ (¬¬p ∧ ¬q) ∨ (¬¬q ∧ ¬p)
ou seja:
¬(p ↔ q) ⇔ (p ∧ ¬q) ∨ (¬p ∧ q)
Exemplo
p q ¬p ¬q p∧¬q ¬p∧q (p∧¬q) ∨ (¬p∧q) p↔q ¬(p↔q)
V V F F F F F V F
V F F V V F V F V
F V V F F V V F V
F F V V F F F V F

Dedução
Definição
Dado um argumento P1, P2 e P3 → Q chama-se demonstração ou
dedução de Q a partir das premissas P1, P2, . . . Pn, a sequência finita de
proposições X1, X2, . . . Xm, tal que cada Xi ou é uma premissa ou decorre
logicamente de proposições anteriores da sequência, e de tal modo que a
última proposição Xm seja a conclusão Q do argumento dado.
Desta forma, se for possível obter a conclusão Q através do procedimento
de dedução, o argumento é válido, caso contrário, não é válido.
O método dedutivo é mais eficente para demonstração de implicações e
equivalências lógicas do que quando utiliza-se de tabelas-verdade.

Demonstração da Implicação I
Implicação
p ∧ q ⇒ p
Exemplo
p ∧ q → p ⇔
¬(p ∧ q) ∨ p ⇔
(¬p ∨ ¬q) ∨ p ⇔
(¬p ∨ p) ∨ ¬q ⇔
Tautologia ∨¬q ⇔
Tautologia

Demonstração da Implicação II
Implicação
(p → q) ∧ p ⇒ q
Exemplo
(p → q) ∧ p ⇔
(¬p ∨ q) ∧ p ⇔
(p ∧ ¬p) ∨ (p ∨ q) ⇔
Contradição ∨(p ∨ q) ⇔
p ∨ q ⇒
q (Absorção)

Demonstração da Equivalência I
Equivalência
p → q ⇔ p ∨ q → q
Exemplo
p ∨ q → q ⇔
¬(p ∨ q) ∨ q ⇔
(¬p ∧ ¬q) ∨ q ⇔
(¬p ∨ q) ∧ (¬q ∨ q) ⇔
(¬p ∨ q) ∧ Tautologia ⇔
p → q

Demonstração da Equivalência II
Equivalência
(p → q) ∧ (p → ¬q) ⇔ ¬p
Exemplo
(¬p ∨ q) ∧ (¬p ∨ ¬q) ⇔
¬p ∨ (q ∧ ¬q) ⇔
¬p∨ Contradição ⇔
¬p

Forma Normal das Proposições
Deﬁnição
Uma proposição está na forma normal (FN) se e somente se, quando
muito, contém apenas os conectivos: ¬, ∧ e ∨.
Exemplo
¬p ∧ q, ¬(p ∨ ¬q) ou p ∨ (p ∧ q)
Há duas representações de formas normais para uma proposição:
Forma normal conjuntiva (FNC); e
Forma normal disjuntiva (FND).

Forma Normal Conjuntiva
Deﬁnição
Uma proposição está na forma normal conjuntiva (FNC) se e somente se
são veriﬁcadas as seguintes condições:
Contém, quanto muito, os conectivos: ¬, ∧ e ∨;
O conectivo de negação ¬ não aparece repetido e não tem alcance
sobre os conectivos ∧ e ∨; e
O conectivo ∨ não tem alcance sobre o conectivo ∧.
Exemplo
p ∨ ¬q, p ∧ ¬q ∧ r, e (p ∨ q) ∧ q

Forma Normal Disjuntiva
Deﬁnição
Um proposição está na forma normal disjuntiva (FND) se e somente se são
veriﬁcadas as seguintes condições:
Contém, quando muito, os conectivos: ¬, ∧ e ∨;
O conectivo de negação ¬ não aparece repedito e não tem alcance
sobre os conectivos ∧ e ∨; e
O conectivo ∧ não tem alcance sobre o conectivo ∨.
Exemplo
p ∨ ¬q, p ∨ ¬q ∨ r, e (p ∧ q) ∨ q

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Argumento
Definição
Chama-se argumento toda a afirmação de que uma dada sequência finita
P1, P2, . . . , Pn(n ≥ 1) de proposições tem como consequência ou
acarreta uma proposição final Q.
Um argumento de premissas P1, P2, . . . , Pn e de conclusão Q indica-se
por:
P1, P2, . . . , Pn Q
Importante
Um argumento P1, P2, . . . , Pn Q é válido se e somente se a condicional:
P1 ∧ P2 ∧ . . . ∧ Pn → Q é tautológica.

Inferência
Definição
É o processo pelo qual se chega a uma proposição, firmada na base de uma
ou outras mais proposições aceitas como ponto de partida do processo.
Um método mais eficiente para demonstrar, verificar ou testar a
validade de um dado argumento P1, P2, . . . , Pn Q consiste em deduzir
a conclusão Q a partir das premissas P1, P2, . . . , Pn mediante o uso de
certas regras de inferência.

Regras de Inferência
Definição
As regras de inferência constituem relações específicas entre proposições:
As regras de inferência são:
Regra de Adição (AD);
Regra de Simplificação (SIMP);
Regra da Conjunção (CONJ);
Regra de Absorção (ABS);
Regra Modus ponens (MP);
Regra Modus tollens (MT);
Regra do Silogismo disjuntivo (SD);
Regra do Silogismo hipotético (SH);
Regra do Dilema construtivo (DC); e
Regra do Dilema destrutivo (DD).

Regra da Adição
Deﬁnição
Dada uma proposição p, dela se pode deduzir a sua disjunção com
qualquer outra proposição, isto é, deduzir p ∨ q, ou p ∨ r, etc.
Exemplo
(i)
p
p ∨ q
(ii)
p
q ∨ p

Regra de Simpliﬁcação
Deﬁnição
Da conjunção p ∧ q de duas proposições se pode deduzir cada uma das
proposições, p ou q.
Exemplo
(i)
p ∧ q
p
(ii)
p ∧ q
q

Regra da Conjunção
Deﬁnição
Permite deduzir de duas proposições dadas p e q (premissas) a sua
conjunção p ∧ q ou q ∧ p (conclusão).
Exemplo
(i)
p
q
p ∧ q
(ii)
p
q
q ∧ p

Regra da Absorção
Deﬁnição
Está regra permite, dada uma condicional p → q como premissa, dela
deduzir como conclusão uma outra condicional com o mesmo antecedente
p e cujo consequente é a conjunção p ∧ q das duas proposições que
integram a premissa, isto é, p → p ∧ q.
Exemplo
p → q
p → (p ∧ q)

Regra Modus Ponens
Deﬁnição
Também é chamada Regra de Separação e permite deduzir q
(conclusão) a partir de p → q e p (premissas).
Exemplo
p → q
p
q

Regra Modus Tollens
Deﬁnição
Permite, a partir das premissas p → q (condicional) e ¬q (negação do
consequente), deduzir como conclusão ¬p (negação do antecedente).
Exemplo
p → q
¬q
¬p

Regra do Silogismo Disjuntivo
Deﬁnição
Permite deduzir da disjunção p ∨ q de duas proposições e da negação ¬p
(ou ¬q) de uma delas a outra proposição q (ou p).
Exemplo
(i)
p ∨ q
¬p
q
(ii)
p ∨ q
¬q
p

Regra do Silogismo Hipotético
Deﬁnição
Esta regra permite, dada duas condicionais: p → q e q → r (premissas),
tais que o consequente da primeira coincide com o antecedente da segunda,
deduzir uma terceira condicional p → r (conclusão) cujo antecedente e
consequente são respectivamente o antecedente da premissa p → q e o
consequente da outra premissa q → r.
Exemplo
p → q
q → r
p → r

Regra do Dilema Construtivo
Deﬁnição
Nesta regra, as premissas são duas condicionais e a disjunção dos seus
antecedentes, e a conclusão é a disjunção dos consequentes destas
condicionais.
Exemplo
p → q
r → s
p ∨ r
q ∨ s

Regra do Dilema Destrutivo
Deﬁnição
Nesta regra, as premissas são duas condicionais e a disjunção da negação
dos seus consequentes, e a conclusão é a disjunção da negação dos
antecedentes destas condicionais.
Exemplo
p → q
r → s
¬q ∨ ¬s
¬p ∨ ¬r

Validade Mediante Regras de Inferência I
Argumento
p → q, p ∧ r q
Exemplo
(1) p → q
(2) p ∧ r
(3) p 2 – SIMP
(4) q 1,3 – MP

Validade Mediante Regras de Inferência II
Argumento
p ∧ q, p ∨ r → s p ∧ s
Exemplo
(1) p ∧ q
(2) p ∨ r → s
(3) p 1 – SIMP
(4) p ∨ r 3 – AD
(5) s 2,4 – MP
(6) p ∧ s 3,5 – CONJ

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Demonstração Indireta
Deﬁnição
Um método frequentemente empregado para demonstrar a validade de
um dado argumento:
P1, P2, . . . , Pn Q
chamado também por “Demonstração por Absurdo” consiste em admitir a
negação ¬Q da conclusão Q, isto é, supor ¬Q verdadeira, e daí deduzir
logicamente uma contradição qualquer C a partir das premissas
P1, P2, . . . Pn e ¬Q, isto é, demonstrar que é válido o argumento:
P1, P2, . . . , Pn, ¬Q C

Validade Mediante Demonstração Indireta I
Argumento
p → ¬q, r → q ¬(p ∧ r)
Exemplo
(1) p → ¬q
(2) r → q
(3) p ∧ r Negação de Q
(4) p 3 – SIMP
(5) r 3 – SIMP
(6) ¬q 1,4 – MP
(7) q 2,5 – MP
(8) q ∧ ¬q 6,7 – CONJ (Contradição)

Validade Mediante Demonstração Indireta II
Argumento
¬p → q, ¬q ∨ r, ¬r p ∨ s
Exemplo
(1) ¬p → q
(2) ¬q ∨ r
(3) ¬r
(4) ¬p ∧ ¬s Negação de Q
(5) ¬p 4 – SIMP
(6) q 1,5 – MP
(7) ¬q 2,3 – SD
(8) q ∧ ¬q 6,7 – CONJ (Contradição)

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Sentenças Abertas com uma Variável
Deﬁnição
Chama-se sentença aberta com uma variável em um conjunto A, uma
expressão p(x) tal que p(a) é falsa (F) ou verdadeiro (V ) para todo a ∈ A.
Em outros termos, p(x) é uma sentença aberta em A se e somente se p(x)
torna-se uma proposição (verdadeira ou falsa) todas as vezes que se
substitui a variável x por qualquer elemento a do conjunto A(a ∈ A).
Exemplo
São sentenças abertas em N = {1, 2, 3, . . . , n, . . .} as seguintes expressões:
x + 1 > 8
x + 5 = 9
x é primo

Sentenças Abertas com duas Variáveis
Deﬁnição
Dados dois conjuntos A e B, chama-se sentença aberta com duas variáreis
em A ∧ B, uma expressão p(x, y) tal que verdadeira (V ) ou falsa (F) para
todo o par ordenado (a, b) ∈ AxB. Em outros termos, p(x, y) é uma
sentença aberta em AxB se e somente se p(x, y) torna-se uma proposição
(verdadeira ou falsa) todas as vezes que as variáveis x e y são substituídas
respectivamente pelos elementos a e b de qualquer par ordenado (a, b)
pertencente ao produto cartesiano AxB dos conjuntos A e B
((a, b) ∈ AxB).
Exemplo
Sejam os conjuntos A = {1, 2, 3} e B = {5, 6}. São sentenças abertas em
AxB as seguintes expressões:
x é menor que y
x é o dobro de y

Sentenças Abertas com n-Variáveis
Deﬁnição
Chama-se sentença aberta com n variáveis em A1xA2x . . . xAn, uma
expressão p(x1, x2, . . . , xn) tal que p(a1, a2, . . . , an) é verdadeira (V ) ou
falsa (F) para toda n-upla (a1, a2, . . . , an ∈ A1xA2x . . . xAn).
Exemplo
A expressão x + 2y + 3z < 18 é um sentença aberta em NxNxN, na qual, o
termo ordenado (1, 2, 3), satisfaz esta sentença aberta, pois,
1 + 2 ∗ 2 + 3 ∗ 4 < 18.

Operações Lógicas sobre Sentenças Abertas
As operações lógicas que deﬁnimos para proposições estendem-se
naturalmente à sentenças abertas, e como podemos lembrar, são elas:
Não (Negação), ¬ ;
E (Conjunção), ∧;
Ou (Disjunção), ∨;
Se – então (Condicional), →;e
Se e somente se (Bicondicional), ↔.

Operação de Negação
Exemplo
A negação da sentença aberta em R (Conjunto dos números reais):
“x < 2”
Assim, para x = 0, x = −1, x = 2, x = 5, x = π e x = 8, 57, temos
sucessivamente:
x x < 2 ¬(x < 2)
0 V F
-1 V F
2 F V
5 F V
π F V
8,57 F V

Operação de Conjunção
Exemplo
A conjunção das sentenças abertas em R (Conjunto dos números reais):
“x > 2” ∧ “x < 8”
Assim, para x = 5, x = π, x = 2, x = −1 e x = 8, 57, temos
sucessivamente:
x x > 2 x < 8 x > 2 ∧ x < 8
7 V V V
π V V V
2 F V F
-1 F V F
8,57 V F F

Operação de Disjunção
Exemplo
A disjunção das sentenças abertas em R (Conjunto dos números reais):
“x < 2” ∨ “x > 8”
sucessivamente:
x x < 2 x > 8 x < 2 ∨ x > 8
0 V F V
-1 V F V
2 F F F
5 F F F
π F F F
8,57 F V V

Operação Condicional
Exemplo
A condicional das sentenças abertas em R (Conjunto dos números reais):
“x < 2” → “x > 8”
sucessivamente:
x x < 2 x > 8 x < 2 → x > 8
0 V F F
-1 V F F
2 F F V
5 F F V
π F F V
8,57 F V V

Operação Bicondicional
Exemplo
A bicondicional das sentenças abertas em R (Conjunto dos números reais):
“x < 2” ↔ “x > 8”
sucessivamente:
x x < 2 x > 8 x < 2 ↔ x > 8
0 V F F
-1 V F F
2 F F V
5 F F V
π F F V
8,57 F V F

Ementa do Curso
1 Introdução
11 Quantiﬁcadores

Quantificador
Definição
O termo quantificação tem vários significados (gerais e específicos). Ele
cobre toda ação que quantifique observações e experiências, traduzindo-as
para números através da contagem e mensuração. É, portanto, a base para
a matemática e para a ciência. Na linguagem e na lógica, a quantificação é
uma construção que especifica a quantidade de indivíduos de um domínio
de discurso que se aplicam a (ou satisfazem) uma fórmula aberta.
Os dois tipos fundamentais de quantificação na lógica de predicados são:
Universal, ∀x; e
Existencial, ∃x.
Importante
Os quantificadores são interdefiníveis. Isto significa que uma fórmula com
quantificador universal pode ser transformada em uma fórmula que contém
apenas quantificadores existencial e vice-versa.

Quantificador Universal: ∀x
Definição
Seja p(x) um sentença aberta em um conjunto não vazio A(A = ∅) e seja
Vp o seu conjunto-verdade:
Vp = {x|x ∈ A ∧ p(x)}
Quando Vp = A, isto é, todos os elementos do conjunto A satisfazem a
sentença aberta p(x), podemos, então, afirmar:
“Para todo elemento x de A, p(x) é verdadeira (V )”; ou
“Qualquer que seja o elemento x de A, p(x) é verdadeira”.
Exemplo
Todo homem é fiel.
Todo homem é mortal.
Toda criança é verdadeira.

Quantificador Existencial: ∃x
Definição
Seja p(x) um sentença aberta em um conjunto não vazio A(A = ∅) e seja
Vp o seu conjunto-verdade:
Vp = {x|x ∈ A ∧ p(x)}
Quando Vp não é vazio (Vp = ∅), então, um elemento, pelo menos, do
conjunto A satisfaz a sentença abeta p(x), e podemos afirmar:
“Existe pelo menos um x ∈ A” tal que p(x); ou
“Para algum x ∈ A tal que p(x)”.
Exemplo
Existe vida em outros planetas.
Existe mamífero que voa.
Existe cidadão honesto.

Negação de Proposições com Quantificador
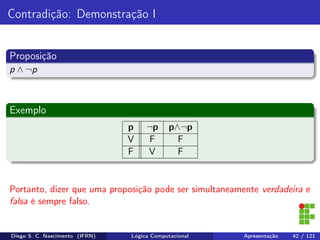
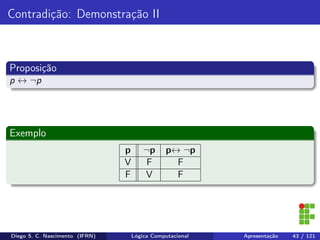
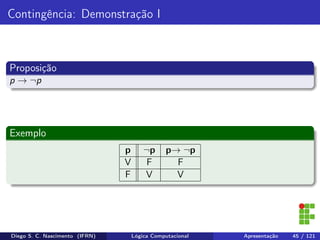
Definição
A negação da proposição (∀x ∈ A)(p(x)) é equivalente a afirmação de que,
para ao menos um x ∈ A, p(x) é falsa ou ¬p(x) é verdadeira. Logo,
subsiste a equivalência:
¬[(∀x ∈ A)(p(x))] ↔ (∃x ∈ A)(¬p(x))
Analogamente, a negação da proposição (∃x ∈ A)(p(x)) é equivalente a
afirmar de que, para todo x ∈ A, p(x) é falsa ou ¬p(x) é verdadeira. Logo,
subsiste a equivalência:
¬[(∃x ∈ A)(p(x))] ↔ (∀x ∈ A)(¬p(x))
Essas duas importantes equivalências são conhecidas por segunda regra
de negação DE MORGAN.

Quantificação Múltipla
Toda a sentença aberta precedida de quantificadores, um para cada
variável, isto é, com todas as variáveis quantificadas, é uma proposição,
pois, assume um dos valores lógicos V ou F.
Exemplo
1 (∀x ∈ A)(∀y ∈ B)(p(x, y));
2 (∀x ∈ A)(∃y ∈ B)(p(x, y)); ou
3 (∃x ∈ A)(∀y ∈ B)(∀z ∈ C)(p(x, y, z)).

Quantiﬁcação Múltipla
Exemplo
Consideramos os conjuntos:
H = {Jorge, Cláudio, Paulo}, M = {Suely, Cármen}
e seja p(x,y) a sentença aberta em HxM:“x é irmão de y”. A proposição:
(∀x ∈ H)(∃y ∈ M)(p(x, y))
se pode ler: “Para todo x de H existe pelo menos um y de M tal que x é
irmão de y.” A proposição:
(∃y ∈ M)(∀x ∈ H)(p(x, y))
se pode ler: “Pelo menos uma das mulheres de M é irmã de todos os
homens de H”.

Comutativa dos Quantificadores
Quantificadores do mesmo tipo podem ser comutados:
Exemplo
(∀x)(∀y)(p(x, y)) ↔ (∀y)(∀x)(p(x, y))
(∃x)(∃y)(p(x, y)) ↔ (∃y)(∃x)(p(x, y))
Quantificadores de tipos diferentes não podem em geral ser
comutados:
Exemplo
(∀x)(∃y)(x é filho de y) = (∃x)(∀y)(x é filho de y)

Logica computacional

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Logica computacional

Logica computacional