O documento discute conceitos básicos de eletrônica, incluindo:
1) Apresenta o professor Antonio Carlos Kobori e descreve os cursos técnicos do Centro Universitário Moura Lacerda.
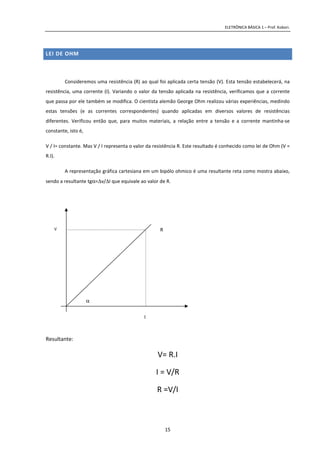
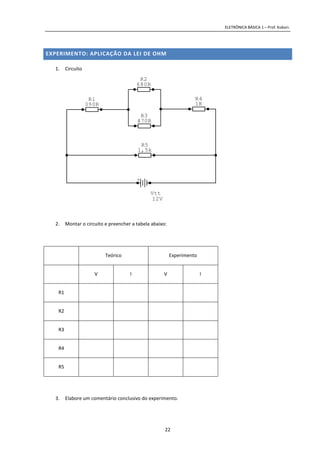
2) Explica as grandezas elétricas fundamentais de tensão, corrente e resistência elétrica e como elas se relacionam.
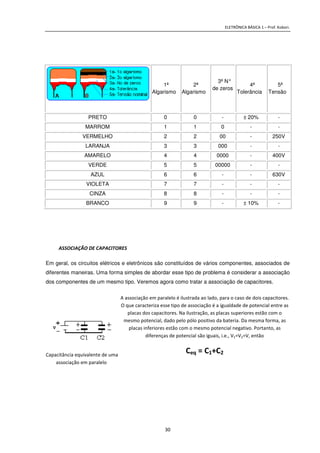
3) Discutem representações de valores através de notação científica e prefixos métricos.