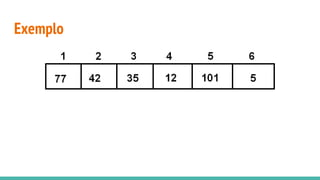
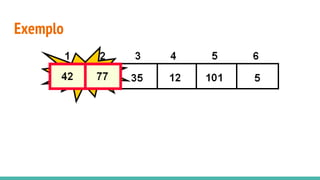
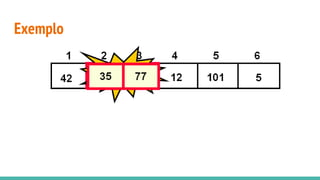
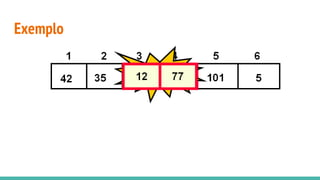
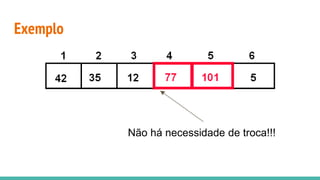
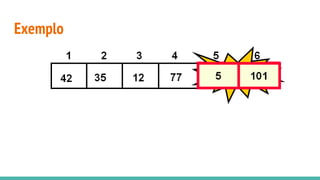
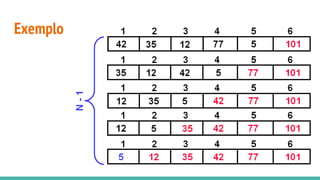
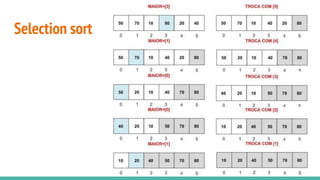
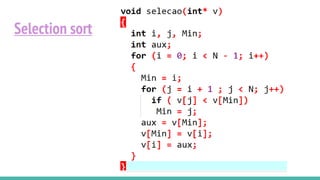
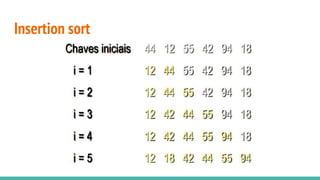
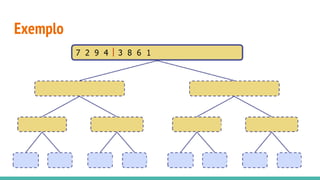
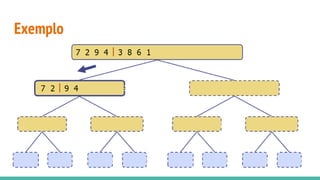
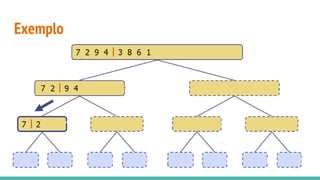
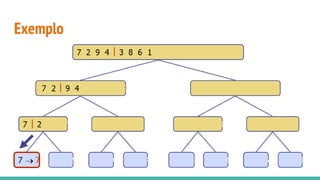
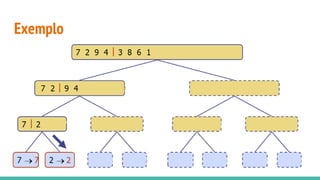
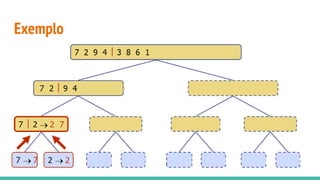
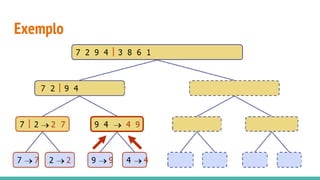
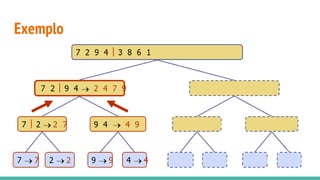
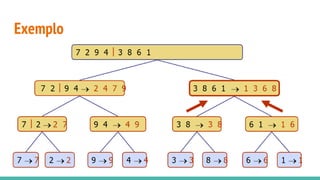
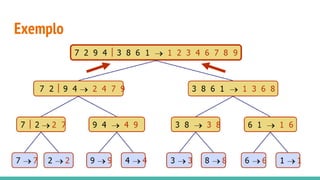
O documento discute algoritmos de ordenação. Apresenta os algoritmos Bubble sort, Selection sort e Insertion sort, explicando seus passos e complexidades. Também aborda o método "dividir para conquistar" e apresenta exemplos como o algoritmo de exponenciação e o Merge sort.










































![Merge sort
void merge(int vetor[], int inicio, int meio, int fim){
int tamanho = fim - inicio + 1;
int i, j, k, posicao;
int temp[tamanho];
for (i=inicio; i<=fim; i++) {
temp[i] = vetor[i];
}
for (i=inicio, j=meio+1, posicao=inicio; (i <= meio) && (j <= fim); posicao++) {
if(temp[i]<temp[j]){
vetor[posicao] = temp[i];
i ++;
}
else{
vetor[posicao] = temp[j];
j++;
}
}](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-63-320.jpg)
![Merge sort
if(i == meio+1){
for(k=j; k<=fim; k++){
vetor[posicao] = temp[k];
posicao++;
}
}
else {
for(k=i; k<=meio; k++){
vetor[posicao] = temp[k];
posicao++;
}
}
}](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-64-320.jpg)



![Quick sort
A parte mais delicada do método é o processo de partição.
O vetor A [Esq..Dir] é rearranjado por meio da escolha arbitrária de um pivô
x.
O vetor A é particionado em duas partes:
Parte esquerda: chaves ≤ x.
Parte direita: chaves > x.](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-68-320.jpg)
![Partição
1. Escolha arbitrariamente um pivô x.
2. Percorra o vetor a partir da esquerda até que A[i] > x.
3. Percorra o vetor a partir da direita até que A[j] ≤ x.
4. Troque A[i] com A[j].
5. Continue este processo até os apontadores i e j se cruzarem.](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-69-320.jpg)
![Partição
1. Escolha arbitrariamente um pivô x.
2. Percorra o vetor a partir da esquerda até que A[i] > x.
3. Percorra o vetor a partir da direita até que A[j] ≤ x.
4. Troque A[i] com A[j].
5. Continue este processo até os apontadores i e j se cruzarem.](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-70-320.jpg)
![Após a partição
O vetor A[Esq..Dir] está particionado de tal forma que:
Os itens em A[Esq], A[Esq + 1], ..., A[j] são menores ou iguais a x;
Os itens em A[i], A[i + 1], ..., A[Dir] são maiores ou iguais a x.](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-71-320.jpg)
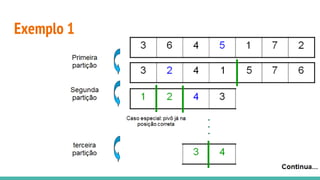
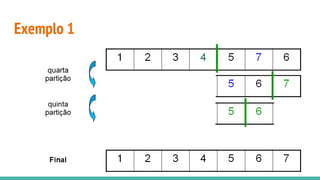
![Exemplo 1
O pivô x é escolhido como sendo:
O elemento central: A[(i + j) / 2].
Exemplo:
3 6 4 5 1 7 2](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-72-320.jpg)
![Quick sort
void Particao(int Esq, int Dir, int *i, int *j, Item *A){
Item x, aux;
*i = Esq; *j = Dir;
x = A[(*i + *j)/2]; /* obtem o pivo x */
do{
while (x.Chave > A[*i].Chave) (*i)++;
while (x.Chave < A[*j].Chave) (*j)--;
if (*i <= *j){
aux = A[*i]; A[*i] = A[*j]; A[*j] = aux;
(*i)++; (*j)--;
}
} while (*i <= *j);
}](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-75-320.jpg)





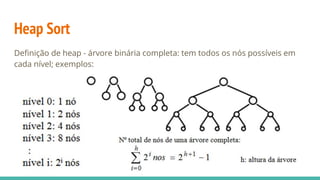

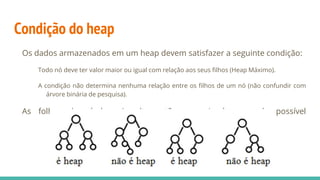
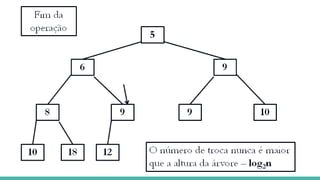
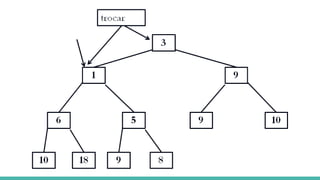
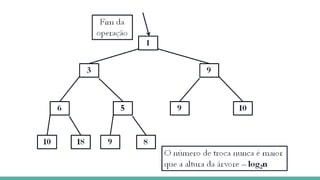
![Relacionando os nós do Heap
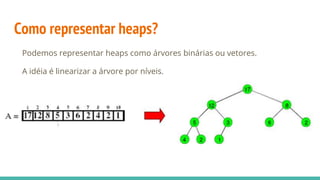
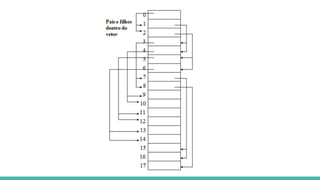
A representação em vetores permite relacionar os nós do heap da seguinte
forma:
raiz da árvore: primeira posição do vetor
filhos de um nó na posição i: posições 2i e 2i+1
pai de um nó na posição i: posição [i / 2]](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-85-320.jpg)
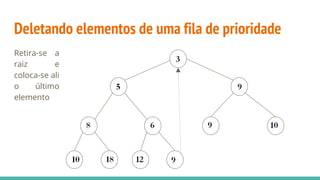
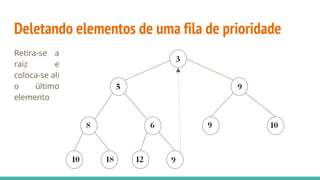
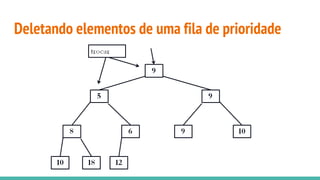
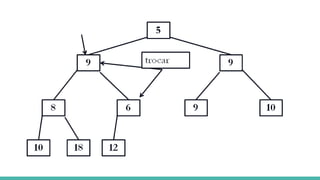
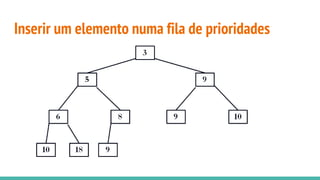
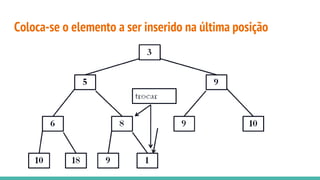
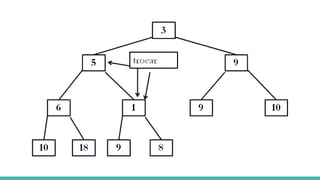


![Heap sort
void FormarFilaPrioridades (int n, vetor V) {
int i, j, temp;
for (i = n-2; i >= 0; i--) {
j = i;
while (j < n-1 && V[j] < V[n-(n-j)/2]) {
temp = V[j];
V[j] = V[n-(n-j)/2];
V[n-(n-j)/2] = temp; j = n-(n-j)/2;
}
}
}](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-101-320.jpg)
![Heap sort
void OrdenarFilaPrioridades (int n, vetor V) {
int i, j, k, temp, min; bool parou;
for (i = 0; i < n-1; i++) {
min = V[n-1]; V[n-1] = V[i]; V[i] = min;
parou = false; j = n-1;
while (! parou && 2*j-n > i) {
if (2*j-n == i+1 || V[2*j-n] < V[2*j-n-1])
k = 2*j-n;
else k = 2*j-n-1;
if (V[j] > V[k]) {
temp = V[j]; V[j] = V[k];
V[k] = temp; j = k;
}
else parou = true;
}
}
}](https://image.slidesharecdn.com/algoritmosdeordenao-170406142738/85/Algoritmos-de-ordenacao-102-320.jpg)

