[1] O documento discute métodos numéricos para aproximar o valor de integrais definidas, como o Método dos Trapézios e o Método de Simpson. [2] Estes métodos aproximam a função f por uma função mais simples p cuja primitiva é mais fácil de calcular. [3] O Método dos Trapézios aproxima a área sob a curva f(x) pela soma das áreas de trapézios formados pelos pontos da função em intervalos igualmente espaçados entre o limite inferior e superior da integral.

1. INTEGRAÇÃO NUMÉRICA
Profa. Luciana Montera
montera@facom.ufms.br
Faculdade de Computação – Facom/UFMS
Métodos Numéricos

2. Integração Numérica
• Integral definida
Integração Numérica
Integral definida
li õ• Aplicações
• Métodos Integração Numérica
– Fórmula de Newton‐Cotesó u a de e o o es
• Método dos Trapézios
• Método de Simpson
Métodos Numéricos

3. Integral DefinidaIntegral Definida
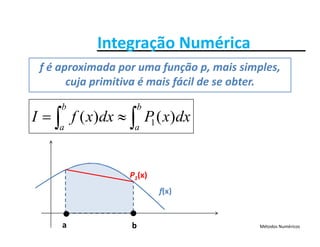
Seja f uma função contínua no intervalo [a b] daSeja f uma função contínua no intervalo [a, b] da
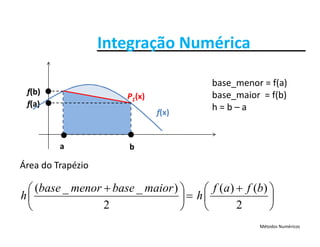
qual se conhece a primitiva F. O valor da
integral definida de f pode ser calculada usando ag f f p
fórmula de Newton‐Leibniz:
)()()( aFbFdxxfI
b
a
 a
Métodos Numéricos

4. Integração NuméricaIntegração Numérica
O ét d d i t ã é i i‐ Os métodos de integração numérica aproximam
valores de integrais definidas.
‐ A integração numérica é útil quando:
‐ Não se conhece a função f. Tem‐se apenasç f p
uma tabela de valores para f.
‐ f é conhecida mas é muito complexa, o que
dificulta a determinação de sua primitiva
Métodos Numéricos

5. Integração NuméricaIntegração Numérica
O ét d d i t ã é i i‐ Os métodos de integração numérica aproximam
valores de integrais definidas.
f é aproximada por uma função p, mais simples,
cuja primitiva é mais fácil de se obtercuja primitiva é mais fácil de se obter.
dxxpdxxfI
b
a
b
a
)()(  
Métodos Numéricos

6. Integração NuméricaIntegração Numérica
f é aproximada por uma função p, mais simples,
bb

cuja primitiva é mais fácil de se obter.
dxxpdxxfI
b
a
b
a
)()(  
f(x)
Métodos Numéricosa b

7. Integração NuméricaIntegração Numérica
f é aproximada por uma função p, mais simples,
bb

cuja primitiva é mais fácil de se obter.
dxxpdxxfI
b
a
b
a
)()(  
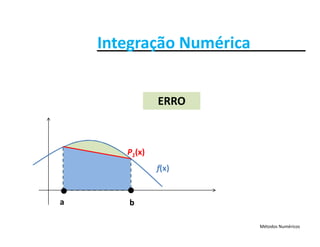
I = área delimitada por f(x) no intervalo [a, b]
f(x)
Métodos Numéricosa b

8. Integração NuméricaIntegração Numérica
f é aproximada por uma função p, mais simples,
bb

cuja primitiva é mais fácil de se obter.
dxxPdxxfI
b
a
b
a
)()( 1 
f(x)
P1(x)
Métodos Numéricosa b

9. Integração NuméricaIntegração Numérica
f é aproximada por uma função p, mais simples,
cuja primitiva é mais fácil de se obter.
bb
 dxxPdxxfI
b
a
b
a
)()( 1 
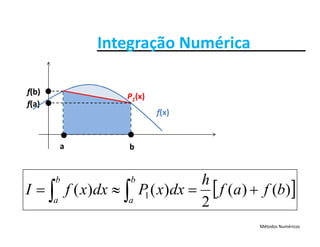
I ≈ área delimitada por P1(x) no intervalo [a, b]
f(x)
P1(x)
Métodos Numéricosa b

10. Integração NuméricaIntegração Numérica
f(a)
P1(x)
f(b)
base_menor = f(a)
base_maior = f(b)
h = b – af(x)
f( ) h = b a
Área do Trapézio
ba





 





 
2
)()(
2
)__( bfaf
h
maiorbasemenorbase
h
Métodos Numéricos
 22

11. Integração NuméricaIntegração Numérica
f(a)
P1(x)
f(b)
f(x)
f( )
ba
 )()(
2
)()( 1 bfaf
h
dxxPdxxfI
b
a
b
a
 
Métodos Numéricos
2aa 

12. Integração NuméricaIntegração Numérica
ERRO
f(x)
P1(x)
f(x)
ba
Métodos Numéricos
ba

13. Métodos de Integração NuméricaMétodos de Integração Numérica
Método dos Trapézios
Método de Simpsonp
Métodos Numéricos

14. Método dos TrapéziosMétodo dos Trapézios

b
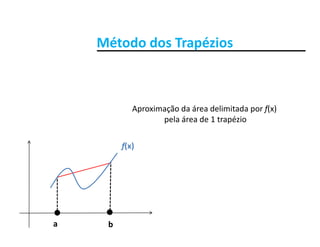
Seja . Considere a subdivisão do intervalo [a, b] em n
Subintervalos [x x ] de comprimento h > 0 Assim temos:
a
dxxf )(
Subintervalos [xi, xi+1] de comprimento h > 0. Assim temos:
Métodos Numéricos

15. Método dos Trapézios

b
Método dos Trapézios
Seja . Considere a subdivisão do intervalo [a, b] em n
Subintervalos [x x ] de comprimento h > 0 Assim temos:
a
dxxf )(
Subintervalos [xi, xi+1] de comprimento h > 0. Assim temos:
• h = (b – a)/n
• xi = a + ih, i = 0, ..., n
f(b)
f(x)
f(a)
f(b)
ba

16. Método dos Trapézios

b
Método dos Trapézios
Seja . Considere a subdivisão do intervalo [a, b] em n
Subintervalos [x x ] de comprimento h > 0 Assim temos:
a
dxxf )(
Subintervalos [xi, xi+1] de comprimento h > 0. Assim temos:
• h = (b – a)/n
• xi = a + ih, i = 0, ..., n
f(b)
f(x)
f(a)
f(b)
iI1

x
hi
ba
i
xi xi+1
)(
2
)( 11   ii
x
i ff
h
dxxPI
i

17. Método dos TrapéziosMétodo dos Trapézios
Aproximação da área delimitada por f(x)Aproximação da área delimitada por f(x)
pela área de 1 trapézio
f(x)
a b

18. Método dos TrapéziosMétodo dos Trapézios
Aproximação da área delimitada por f(x)Aproximação da área delimitada por f(x)
pela somatória da área de n = 5 trapézios
ba

19. Método dos TrapéziosMétodo dos Trapézios
Aproximação da área delimitada por f(x)Aproximação da área delimitada por f(x)
pela somatória da área de n = 5 trapézios
)()( 11
1
 

ii
x
i ff
h
dxxPI
i
)(
2
)( 11  ii
x
i ffdxxPI
i
ba

20. Método dos TrapéziosMétodo dos Trapézios
Aproximação da área delimitada por f(x)Aproximação da área delimitada por f(x)
pela somatória da área de n = 5 trapézios
)()( 11
1
 

ii
x
i ff
h
dxxPI
i
)(
2
)( 11  ii
x
i ffdxxPI
i
n
ba


n
i
iII
0

21. Método dos TrapéziosMétodo dos Trapézios
)(
2
)( 11
1
 

ii
x
x
i ff
h
dxxPI
i
ii




1
0
n
i
iII
 0i

22. Método dos TrapéziosMétodo dos Trapézios
)(
2
)( 11
1
 

ii
x
x
i ff
h
dxxPI
i
ii




1
0
n
i
iII
 



1
0
1
0
2
n
i
ii
i
ff
h

23. Método dos TrapéziosMétodo dos Trapézios
)(
2
)( 11
1
 

ii
x
x
i ff
h
dxxPI
i
ii
n
i
iII 



1
0
 
n
i
ii
i
ff
h




1
0
1
0
2
        nn ffffffff
h
 1322110 ...
2

24. Método dos TrapéziosMétodo dos Trapézios
)(
2
)( 11
1
 

ii
x
x
i ff
h
dxxPI
i
ii
 


1
0
n
i
iII
  



1
0
1
0
2
n
i
ii
i
ff
h
        
  
 1322110 ...
2
nn ffffffff
h
   














 




1
1
0
1
1
0
2
2
2
n
i
i
n
n
i
in f
ff
hfff
h

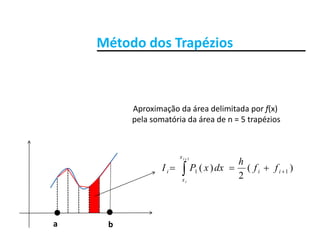
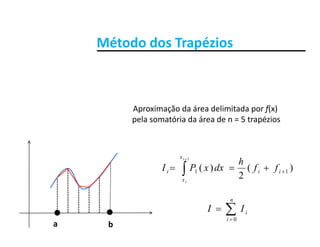
25. Método dos TrapéziosMétodo dos Trapézios

b
Seja . Considere a subdivisão do intervalo [a, b] em n
Subintervalos [x x ] de comprimento h > 0 Assim temos:
a
dxxf )(
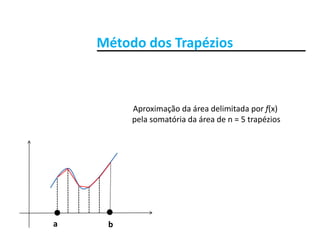
Subintervalos [xi, xi+1] de comprimento h > 0. Assim temos:
• h = (b – a)/n
• x = a + ih i = 0 n• xi = a + ih, i = 0, ..., n
 













 
 
1
0
2
n
i
n
f
ffab
I 



12 in

26. Método dos TrapéziosMétodo dos Trapézios
Exemplo:
Seja o intervalo [3 0 3 6] e a seguinte integral:xf
1
)( 
Exemplo:
Seja , o intervalo [3,0, 3,6] e a seguinte integral:
x
xf )(
dxxf
6,3
)( dxxf0,3
)(
Calcule:
• o valor aproximado da integral para n = 1
l i d d i t l 6• o valor aproximado da integral para n = 6
• o valor exato da integral

27. Método dos TrapéziosMétodo dos Trapézios
Exemplo:
Seja o intervalo [3 0 3 6] e n = 1 Calcule o valorxf
1
)( 
Exemplo:
Seja , o intervalo [3,0, 3,6] e n 1. Calcule o valor
aproximado da Integral:
x
xf )(
6,3
dxxf
6,3
0,3
)(

28. Método dos TrapéziosMétodo dos Trapézios
Exemplo:
Seja o intervalo [3 0 3 6] e n = 1 Calcule o valorxf
1
)( 
Exemplo:
Seja , o intervalo [3,0, 3,6] e n 1. Calcule o valor
aproximado da Integral:
x
xf )(
6,3
dxxf
6,3
0,3
)(
Solução:
  
a = 3,0
b = 3,6
 













 
 


1
1
0
2
n
i
i
n
f
ff
n
ab
I f0 = 1/3,0 = 0,333
fn = 1/3,6 = 0,278
n = 1
1833,0I

29. Método dos TrapéziosMétodo dos Trapézios
Exemplo:
Seja o intervalo [3 0 3 6] e n = 6 Calcule o valorxf
1
)( 
Exemplo:
Seja , o intervalo [3,0, 3,6] e n 6. Calcule o valor
aproximado da Integral:
x
xf )(
6,3
dxxf
6,3
0,3
)(

30. Método dos TrapéziosMétodo dos Trapézios
Solução:Solução:
a = 3,0
b = 3,6
n = 6
h = (3 6 – 3)/6 = 0 1h = (3,6 – 3)/6 = 0,1
f0 = 1/3,0 = 0,3333 f1 = 1/3,1 = 0,3225
f2 = 1/3,2 = 0,3125 f3 = 1/3,3 = 0,3030
f4 = 1/3,4 = 0,2941 f5 = 1/3,5 = 0,2857
f6 = 1/3,6 = 0,2778f6 1/3,6 0,2778

31. Método dos TrapéziosMétodo dos Trapézios
Solução:Solução:
 
2
1
0













 
 
n
i
n
f
ffab
I
2778033330
2 1
 




i
if
n
 2857,02941,03030,03125,03225,0
2
2778,03333,0
1,0 










 

  8234,1*1,05158,13056,01,0 
1823,0

32. Método dos TrapéziosMétodo dos Trapézios
Exemplo:Exemplo:
Seja , e o intervalo [3,0, 3,6]. Calcule o valor exato da
x
xf
1
)( 
Integral:
dxxf
6,3
)(f0,3
)(

33. Método dos TrapéziosMétodo dos Trapézios
Solução:Solução:
)ln()(
1
)(  xxF
x
xf
63
x
)0,3()6,3()(
6,3
0,3
 FFdxxf
09861,128093,1
)0,3ln()6,3ln(


18232,0
09861,128093,1


34. Método dos TrapéziosMétodo dos Trapézios
Exercício:
Seja , o intervalo [0, 1] e a seguinte integral:
x
exf )(
Exercício:
dxxf
1
)(0
Calcule:
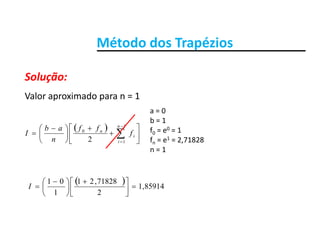
• o valor aproximado da integral para n = 1
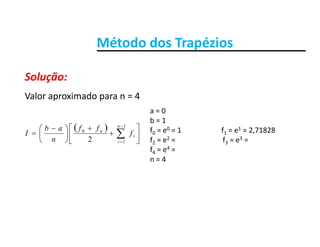
• o valor aproximado da integral para n = 4
• o valor aproximado da integral para n = 4o valor aproximado da integral para n 4
• o valor exato da integral
• o erro cometido em cada aproximação

35. Método dos TrapéziosMétodo dos Trapézios
Solução:
Valor aproximado para n = 1
Solução:
 













 
 
1
0
2
n
i
n
f
ff
n
ab
I
a = 0
b = 1
f0 = e0 = 1
f e1 2 71828 12 in fn = e1 = 2,71828
n = 1
  85914,1
2
71828,21
1
01





 





 
I

36. Método dos TrapéziosMétodo dos Trapézios
Solução:
Valor aproximado para n = 4
Solução:
 













 
 
1
0
2
n
i
n
f
ff
n
ab
I
a = 0
b = 1
f0 = e0 = 1 f1 = e1 = 2,71828
f e2 f e3
 12 in f2 = e2 = f3 = e3 =
f4 = e4 =
n = 4