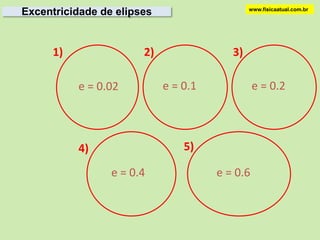
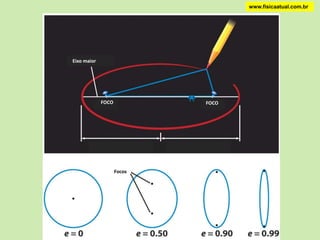
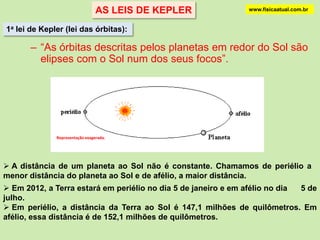
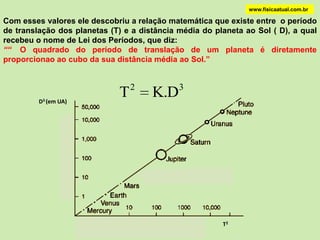
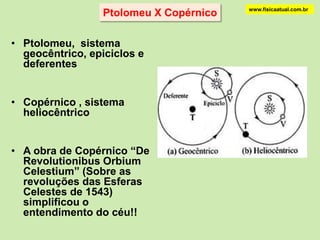
1) O documento descreve as teorias cosmológicas de Platão, Aristóteles, Hiparco, Ptolomeu, Copérnico, Galileu e Kepler sobre o sistema solar. 2) Kepler formulou três leis sobre o movimento dos planetas com base nas observações de Tycho Brahe, estabelecendo que as órbitas são elípticas com o Sol em um dos focos. 3) A revolução copernicana propôs que o Sol, e não a Terra, estava no centro do sistema solar, contrariando a visão geocêntrica de Ptol

1. www.fisicaatual.com.brGRAVITAÇÃO UNIVERSAL

2. www.fisicaatual.com.brPLATÃO (427 – 347 a.C.) Considerava: a Terra sólida, fixa e no centro do universo (Teoria Geocêntrica).

3. As estrelas eram eternas e imutáveis e pendiam sobre a esfera celeste,com movimento uniforme, descrevendo a cada dia uma órbita perfeitamente circular ao redor da Terra.

4. O Sol era mantido pela esfera solar,menor que a esfera das estrelas e girava em torno da Terra.

5. Conhecia 5 planetas, cada um mantido em sua respectiva esfera: Mercúrio, Vênus, Marte, Júpiter e Saturno.www.fisicaatual.com.brARISTÓTELES (384 a.C. – 322 a.C. Estudou as eclipses e as marés.

6. Apoiou a Teoria Geocêntricawww.fisicaatual.com.brHIPARCO (190 a.C. - 120 a.C.) Fez um catálogo de estrelas de acordo com a sua luminosidade aparente.

7. Descobriu o movimento retrógrado dos planetas. Ora os planetas se movem no mesmo sentido do Sol e da Lua (movimento direto), ora se movem em sentido oposto (movimento retrógrado).CLÁUDIO PTOLOMEU (100 d.C. – 170 d.C.) Quais são as combinações de movimento circular com velocidade constante que existem que serão capazes de explicar essas mudanças peculiares e regulares no céu? ( “ Almagesto, volume 13, publicado no ano de 143 d.C., por Ptolomeu.)Para responder essa pergunta, criou um modelo em 3-D para o movimento de corpos celeste que permitiu prever a posição de planetas com um erro inferior a 20 .www.fisicaatual.com.br

8. www.fisicaatual.com.brPtolomeu explicou o movimento dos planetas através de uma combinação de círculos: o planeta se move ao longo de um pequeno círculo chamado epiciclo, cujo centro se move em um círculo maior chamado deferente. A Terra fica numa posição um pouco afastada do centro do deferente (portanto o deferente é um círculo excêntrico em relação à Terra). Para dar conta do movimento não uniforme dos planetas, Ptolomeu introduziu ainda o equante, que é um ponto ao lado do centro do deferente oposto à posição da Terra, em relação ao qual o centro do epiciclo se move a uma taxa uniforme.

9. www.fisicaatual.com.brSolVenusModelo Geocêntrico de PtolomeuMercurioTLunaMarteJúpiterSaturno

10. Modelo heliocêntrico de Copérnicowww.fisicaatual.com.brA medida que se conhecia melhor os movimentos dos planetas, o Sistema Geocêntrico apresentava problemas crescentes. Desde a Grécia Antiga o sistema de epicíclos vinha sendo modificado com a adição de novos epicíclos sobre os epicíclos. No século XVI surgiu uma obra devida ao polonês Nicolau Copérnico onde se assumia uma nova proposta para o universo que propunha que o Sol estivesse no centro do universo. Os planetas descreviam círculos em torno do Sol. Este sistema é conhecido como Heliocêntrico.É importante observar que a proposta do Sistema Heliocêntrico consistia na retomada de uma proposta feita anteriormente na Grécia Antiga. Ela significava, no entanto, uma mudança filosófica radical pois tirava o homem do centro do universo.

11. O movimento de retorno dos planetas pode ser explicado facilmente no modelo heliocêntrico. Isto pode ser visto na figura a seguir. O movimento retrógrado se deve unicamente a um problema de perspectiva. Apesar da direção dos movimentos dos planetas nas suas órbitas serem sempre os mesmos, como a Terra e o planeta se movem com velocidades diferentes, existem épocas em que a Terra avança mais depressa que o planeta. Nestas épocas, quem observa os planetas da Terra os vê movendo em direção contrária. movimento retrógrado ocorre aqui.JúpiterTerrawww.fisicaatual.com.br

12. Ptolomeu X Copérnicowww.fisicaatual.com.brPtolomeu, sistema geocêntrico, epiciclos e deferentesCopérnico , sistema heliocêntricoA obra de Copérnico “De Revolutionibus OrbiumCelestium” (Sobre as revoluções das Esferas Celestes de 1543) simplificou o entendimento do céu!!

13. COPÉRNICOwww.fisicaatual.com.brCopérnico deduziu a escala relativa de distâncias no sistema solar. rT, a distância Sol-Terra, é hoje a unidade astronômica (U.A.).O eixo da Terra tem uma direção fixa no espaço (23,50 com a normal). É verão no hemisfério sul quando o Sol está mais próximo do Trópico de Capricórniowww.fisicaatual.com.brGALILEUGalileu Galilei (1564-1642) construiu em 1609 um telescópio que ampliava de um fator 1000 o poder de observação.Notou que Júpiter apresentava fases como a lua concluindo que não tinha luz própriaPublicou estas descobertas em “Sidereus Nuncius” ( O Mensageiro das Estrelas” em 1610).Em 1632 publicou “Diálogo sobre os Dois Principais Sistemas do Mundo, o Ptolomaico e o Copernicano”onde defendia o ponto de vista de CopérnicoEm 1633 Galileu foi julgado pelo Santo Ofício e obrigado a abjurar seus “erros e heresias”. Foi condenado à prisão domiciliar. Neste período de 9 anos até sua morte escreveu secretamente “Diálogos sobre Duas Novas Ciências”.Galileu se convenceu que Copérnico estava correto por meio de observações do Sol, Vênus e as luas de Júpiter, usando o telescópio recém inventado.Talvez o fato de entender o que é inércia é que levou Galileu a defender as idéias de Copérnico.

14. www.fisicaatual.com.brEm 1610 Galileu descobriu 4 satélites de Júpiter:

15. TYCHO BRAHE www.fisicaatual.com.brTycho Brahe (1546-1601) dinamarquês, fez observações no século 16.Montou um grande observatório em Uraniborg com o apoio do rei Frederico II. Projeto comparável aos grandes aceleradores de hoje.Observações feitas a olho nu, porém com instrumentos de grandes proporções e precisão.As medições das posições planetárias feitas por Tycho Brahe estavam em desacordo com o modelo de Ptolomeu. Baseado nisto Brahe, que já era conhecido em toda a Europa, desenvolveu o seu próprio modelo do Sistema Solar no qual o Sol e a Lua estavam em órbita em torno da Terra, mas os planetas restantes estavam em órbita em torno do Sol.

16. www.fisicaatual.com.brO Sol e a Lua giravam em torno da Terra. Mercúrio, Vênus, Marte, Júpiter e Saturno giravam em torno do Sol.SOLTERRALUA

17. Johannes Kepler (1571- 1630)www.fisicaatual.com.brJohannes Kepler (1571-1630) foi assistente de Tycho Brahe e seu sucessor no observatório.Tycho Brahe morreu um ano após o início da colaboração deixando seu legado de observações.Após 4 anos de trabalhos mostrou que se usasse o Sol como centro do sistema planetário obtinha melhor acordo com a experiência.Porém Marte apresentava um problema. Na órbita de Marte existia um erro e 8 minutos de arco. As medidas de Brahe eram precisas em pelo menos 4 minutos de arco. Este erro é muito pequeno, porém Kepler se baseou nele para criar o seu modelo. Afirmou: “Construirei uma teoria do universo baseada na discrepância de 8 minutos de arco”.Kepler trabalhou por dois anos e abandonou idéias pré - concebidas como as órbitas circulares do modelo platônico.O resultado foi que a órbita de Marte seria uma elipse com o Sol em um dos seus focos. Este mesmo resultado valeria para outros planetas

18. Elipsewww.fisicaatual.com.brA e B são os vértices da elipse e a medidas do segmento AB (eixo maior) é igual a 2a;

19. CD é o eixo menor e mede 2b

20. F1 e F2 são os focos e a distância entre F1 e F2 é chamada de distância focal e a medida de F1F2 é igual a 2e;

21. O ponto médio da distância focal é o centro da elipse.

22. A razão entre c e a é chamada de excentricidade e está entre 0 e 1.www.fisicaatual.com.brExcentricidade de elipses1)2)3)e = 0.1e = 0.2e = 0.025)4)e = 0.4e = 0.6

23. www.fisicaatual.com.brEixo maiorEixo maiorFOCOFOCOFocos

24. AS LEIS DE KEPLERwww.fisicaatual.com.br1a lei de Kepler (lei das órbitas):“As órbitas descritas pelos planetas em redor do Sol são elipses com o Sol num dos seus focos”.Representação exagerada. A distância de um planeta ao Sol não é constante. Chamamos de periélio a menor distância do planeta ao Sol e de afélio, a maior distância.

25. Em 2012, a Terra estará em periélio no dia 5 de janeiro e em afélio no dia 5 de julho.

26. Em periélio, a distância da Terra ao Sol é 147,1 milhões de quilômetros. Em afélio, essa distância é de 152,1 milhões de quilômetros.www.fisicaatual.com.brA razão e = c/a chama-se excentricidade. Se e = 0 temos órbita circular.Terra: e = 0.017As órbitas dos planetas são virtualmente indistinguíveis de círculos.

27. Os livros exageram na excentricidade da elipse descrita pelos planetas.Na representação abaixo, a Terra ficaria cinco vezes mais perto do Sol em janeiro do que em julho, causando um aumento de 400 por cento em seu diâmetro aparente. Como a intensidade luminosa varia com o inverso do quadrado da distância, isso quer dizer que receberíamos 25 vezes mais luz e calor do Sol em janeiro, se comparássemos com julho. Conclusão: um fim do mundo garantido. Em termos numéricos, sabendo-se que a distância da Terra ao Sol varia de 147,1 a 152,1 milhões de quilômetros, vemos que em janeiro, quanto a Terra está mais próxima do Sol, este fica com um diâmetro aparente que é cerca de 3,4 por cento maior do que em julho , quando a Terra está mais longe dele.www.fisicaatual.com.br

28. www.fisicaatual.com.brSegunda lei de Kepler: Lei das Áreas - “ A linha que une o Sol e o planeta varre as áreas iguais em tempos iguais.”Essa lei mostra que quando um planeta se aproxima do Sol, sua velocidade aumenta; quando se afasta do Sol, sua velocidade diminui. No periélio a velocidade da terra é de 30,3 km/s e no afélio, 29,3 km/s.

29. 3a lei de Kepler (lei dos períodos):www.fisicaatual.com.brKepler conhecia os períodos de translações dos planetas, conhecidos naquela época (de Mercúrio a Saturno), em termos do período de translação da Terra e conhecia também para estes mesmos planetas, suas distâncias médias ao Sol, em termos, também, da distância média da Terra ao Sol. Chamamos a distância média Terra-Sol de Unidade Astronômica e a representamos por UA (1 UA = 149.600.000 km). Enfim, Kepler tinha a seguinte tabela de valores em suas mãos:

30. www.fisicaatual.com.brCom esses valores ele descobriu a relação matemática que existe entre o período de translação dos planetas (T) e a distância média do planeta ao Sol ( D), a qual recebeu o nome de Lei dos Períodos, que diz:““ O quadrado do período de translação de um planeta é diretamente proporcionao ao cubo da sua distância média ao Sol.”D3 (em UA)T2

31. www.fisicaatual.com.brISAAC NEWTON (1642-1727)Isaac Newton (1642-1727) se formou em Cambridge em 1665, neste ano a peste se alastrou por Londres matando 70.000 pessoas. Isto provocou o fechamento da universidade e Newton retornou para a fazenda da família em WoolthorpeNos dois anos que se seguiram Newton deu inestimáveis contribuições a ciência.

32. www.fisicaatual.com.brNas palavras de Newton..“no princípio de 1665 achei o método para aproximar séries e a regra para reduzir qualquer potência de um binômio a tal série”.“No mesmo ano, em maio, achei o método das tangentes de Gregory e Slusius (fórmula de interpolação de Newton) e em novembro o método direto das fluxões” (cálculo diferencial).“No ano seguinte em janeiro a teoria das cores, e em maio os princípios do método inverso das fluxões” (cálculo integral).No mesmo ano comecei a pensar na gravidade como se estendendo até a órbita da lua, e .. da lei de Kepler sobre os planetas ...deduzi que as forças que mantêm os planetas em suas órbitas devem variar com o inverso do quadrado de suas distâncias, tendo então comparado a força necessária para manter a Lua em sua órbita com a força da gravidade na superfície da Terra e encontrado que concordavam bastante bem. Tudo isto foi feito nos dois anos da peste, 1665 e 1666, pois naqueles dias eu estava na flor da idade para invenções e me ocupava mais de matemática e filosofia que em qualquer outra época posterior.

33. www.fisicaatual.com.brPara fazer a mesma bola se mover com velocidade baixa num grande círculo é necessário apenas um fraco puxão.Para fazer a bola se mover com alta velocidade num pequeno círculo é necessário um forte puxão.Para fazer um planeta se mover com baixa velocidade num órbita grande é necessário uma força gravitacional fraca.Para fazer um planeta se mover com alta velocidade num órbita pequena é necessário uma força gravitacional forte.PlanetaPlanetaForçaForçaSolSol

34. Obviamente a Terra exerce uma atração sobre os objetos que estão sobre sua superfície. Newton se deu conta de que esta força se estendia até a Lua e produzia a aceleração centrípeta necessária para manter a Lua em órbita. O mesmo acontece com o Sol e os planetas. Então Newton formulou a hipótese da existência de uma força de atração universal entre os corpos em qualquer parte do Universo. A força centrípeta que o Sol exerce sobre um planeta de massa “m”, que se move com velocidade “v” à uma distância “D” do Sol, é dada por:Assumindo neste instante uma órbita circular, que mais tarde será generalizada para qualquer tipo de órbita, o período “T“ do planeta é dado por: Pela 3a Lei de Kepler: Temos, então:Seja m a massa do planeta e M a massa do Sol. Substituindo-se esta velocidade na expressão da força centrípeta exercida pelo Sol (Fc) no planeta, a força pode então ser escrita como: www.fisicaatual.com.br

35. www.fisicaatual.com.bre, de acordo com a 3a. lei de Newton, o planeta exerce uma força igual e contrária sobre o Sol. A força centrípeta exercida pelo planeta sobre o Sol, de massa M é dada por: Newton deduziu então que:onde G é uma constante de proporcionalidade. Tanto o Sol quanto o planeta que se move em torno dele experimentam a mesma força, mas o Sol permanece aproximadamente no centro do Sistema Solar porque a massa do Sol é aproximadamente mil vezes maior que a massa de todos os planetas somados. Newton então concluiu que para que a atração universal seja correta, deve existir uma força atrativa entre pares de objetos em qualquer região do universo, e esta força deve ser proporcional a suas massas e inversamente proporcional ao quadrado de suas distâncias. A constante de proporcionalidade “G” depende das unidades das massas e da distância.

36. www.fisicaatual.com.brF = força gravitacional entre dois corpos. M1 = massa do primeiro corpo.M2 = massa do segundo corpo.DA constante G é chamada de constante de gravitação universal:Newton demonstrou que corpos esféricos agem para pontos da superfície e do exterior como se toda sua massa estivesse concentrada no centro. Isso deve ser levado em conta na hora de medirmos a distância entre corpos.

37. www.fisicaatual.com.brFORÇA EXERCIDA PELOS ASTROS SOBRE UMA PESSOA DE 70 kg

38. www.fisicaatual.com.brA LUA E A MAÇÃVoltaire conta no livro “Philosophie de Newton” (1738): “Um dia em 1666, Newton, então em sua fazenda, vendo uma fruta cair de uma árvore, segundo disse sua sobrinha, Mme. Conduit, começou a meditar profundamente sobre a causa que atrai todos os corpos em direção ao centro da Terra”. A Lua como a maçã está caindo em direção a Terra. A história é provavelmente apócrifa porém Newton confirma que foi naquele ano que comparou a força necessária para manter a Lua em sua órbita com a gravidade na superfície da Terra.Cálculo da aceleração sobre a Lua no seu movimento em torno da Terra:Newton sabia que:Período da Lua = 27,3 dias = 2,36 x106 s.R = 3,84 x 108 m RE = 6,35 x 106 mRREaLua= ω2R = 0.00272 m/s2

39. www.fisicaatual.com.brNewton determinou que a relação entre a aceleração que a Terra exerce na Lua (a Lua) e a aceleração na superfície da Terra (g = 9,9 m/s2) é: Newton sabia que a relação entre o quadrado da distância da Lua ao centro da Terra (RE) e o quadrado da distância de um ponto na superfície ao centro da Terra (R) é:aLuagRREEssas medidas inspiraram Newton a afirmar que a força de atração gravitacional varia com o inverso do quadrado da distância:

40. ACELERAÇÃO DA GRAVIDADEwww.fisicaatual.com.brA Terra, de massa M e raio R, exerce uma força de atração gravitacional sobre um corpo, de massa m, localizado na sua superfície. A distância entre o centro de gravidade da Terra e o corpo é "d", que é igual ao raio ( d = R ). Desprezando-se os efeitos de rotação da Terra, a força gravitacional será o próprio peso do corpo.mF = PF = PM- F Caso o corpo esteja a uma altura "h" em relação à superfície, a distância "d" passará para R + h e a aceleração gravitacional é modificada para :

41. Quando se leva em conta o efeito da rotação da Terra, o peso só coincide com a força gravitacional nos pólos. O campo gravitacional é variável com a latitude, pois a força gravitacional é decomposta em peso (P) e em força centrípeta (Fc).www.fisicaatual.com.br

42. www.fisicaatual.com.brMOVIMENTO ORBITALA força gravitacional atua como o barbante da figura. Ela obriga a bola a manter-se em movimento circular.Se o barbante arrebentar, a bola passará a se mover, pelo princípio da inércia, em movimento retilíneo uniforme.O movimento de satélites foi compreendido por Newton, que argumentava que a Lua era simplesmente um projétil circundando a Terra sob atração da força gravitacional.

43. Em 8 km, a Terra se curva 4,9 m para baixo em relação a um plano horizontal tangente ao ponto de origem desses 8 km :Imaginemos que um satélite é disparado horizontalmente a uma velocidade de 8 km/s, realizando o que teoricamente se costuma chamar de "vôo rasante". Esse satélite será acelerado em direção ao centro da Terra como qualquer outro corpo em queda livre. No primeiro segundo de vôo, o satélite cai 4,9 x t2 = 4,9 m, isto é, exatamente o mesmo que a Terra se curva em relação ao plano tangente. Por isso, o satélite não estará mais perto nem mais longe da Terra do que estava no segundo anterior. Este argumento pode ser repetido no próximo segundo e em todos os segundos sucessivos. Assim, o satélite nunca atingirá a superfície da Terra embora esteja constantemente caindo tornando-se, de fato, um satélite artificial terrestre, se sua velocidade for, no mínimo 8 000 m/s.www.fisicaatual.com.br

44. www.fisicaatual.com.brNewton explicou como um corpo poderia se manter em órbita. Consideremos o movimento de um corpo lançado inicialmente com uma trajetória horizontal. Por causa de seu peso, o corpo sai de sua trajetória reta, descreve uma curva e cai sobre o solo. Quanto maior a velocidade com que é lançado, mais longe ele alcança antes de cair sobre a Terra. Veja a figura que representa a Terra e as linhas curvas que o corpo percorreria se projetado em uma direção horizontal do topo de uma alta montanha, com velocidades cada vez maiores. Suponha que não há resistência do ar. Aumentando cada vez mais a velocidade inicial do corpo ele cairá cada vez mais longe até que, quando a velocidade inicial for suficientemente grande, acabará percorrendo toda a circunferência da Terra, voltando à montanha de onde foi lançado.

45. www.fisicaatual.com.brVelocidade linear de translação de um satéliteConsiderando a massa de um planeta representado por M, o raio da órbita representado por R ( distância do satélite ao centro da Terra) e a constante gravitacional representada por G, temos que a essa força gravitacional aplicada no satélite pelo planeta, irá realizar o papel de uma resultante centrípeta, vejamos: FgravA velocidade de translação de um satélite possui um módulo que depende tanto da massa do planeta como do raio de sua órbita. Ao se tratar do mesmo planeta, é importante saber que quanto mais próximo o satélite estiver, mais alta será a velocidade de translação .

46. Satélite Rasantewww.fisicaatual.com.brEsse satélite recebe este nome pelo fato de estar junto à superfície da Terra. Desconsiderando todos os efeitos do ar, iremos ter: mF grav = PRMonde: gS = aceleração da gravidade na superfície da Terra = 10 m/s2 R = raio da Terra = 6,4 x 106 m A velocidade orbital de um satélite depende da sua altitude em relação à Terra. Quanto mais próximo da Terra, mais rápida a velocidade orbital precisa ser. A uma altitude de 200 km, a velocidade orbital exigida está um pouco acima de 27.400 km/h. Para manter uma órbita de 35.786 km acima da Terra, um satélite deve orbitar a uma velocidade de aproximadamente 11.300 km/h. A lua tem uma altitude de aproximadamente 384.400 km, a uma velocidade de quase 3.700 km/h e sua órbita leva 27,322 dias

47. www.fisicaatual.com.brEm geral, quanto mais alta é a sua órbita, maior o tempo que um satélite pode permanecer em órbita. Em altitudes mais baixas, o satélite colide com vestígios da atmosfera da Terra, o que causa o arrasto. O arrasto faz com que a órbita decaia até que o satélite volte para dentro da atmosfera e queime. A altitudes maiores, onde o vácuo no espaço é quase total, quase não há arrasto, e o satélite pode ficar em órbita por séculos (como por exemplo, a lua).O grande precursor do acúmulo de detritos no espaço foi o Sputnik, o primeiro satélite artificial da Terra, lançado em 1957 pela antiga União Soviética. Hoje em dia, com a evolução tecnológica, há cerca de 800 satélites ativos em órbita. Enquanto isso, segundo o chefe do laboratório do INPE, a órbita se tornou um “vasto lixão espacial”. De acordo com dados divulgados em 2008 pela NASA, a agência espacial americana, foram contabilizados no espaço aproximadamente 17.000 destroços acima de 10 centímetros, 200.000 objetos com tamanho entre 1 e 10 centímetros e dezenas de milhões de partículas menores que 1 centímetro.

48. www.fisicaatual.com.brTipos de órbitasa) PolarSatélites de orbita polar viajam em orbitas circulares que se deslocam desde um polo ao outro. Dessa maneira, estes satélites podem “ver” a terra 2 vezes em um período de 24 horas.879 km

49. www.fisicaatual.com.brb) Equatorial Se a velocidade de rotação de um satélite equatorial for igual à velocidade de rotação da própria Terra, o satélite mantém-se sempre acima do mesmo ponto sobre o equador. Esse tipo de satélite é chamado de geoestacionário, isto é, parado em relação à Terra (geo). Para que um satélite tenha a mesma velocidade de rotação da Terra (1 volta em 24 horas), sua órbita circular não pode ter qualquer raio. Ele tem que estar a 35 785 km acima de algum ponto do equador.É impossível, por exemplo, colocar um satélite estacionário em cima da cidade de Belo Horizonte. Mas, como a altura do satélite é grande (quase 36.000 km), a área possível de ser alcançada por um sinal vindo do satélite pode cobrir praticamente todo o Brasil.

50. www.fisicaatual.com.brEm 1985, o Brasil lançou seu primeiro satélite doméstico de comunicação, denominado de Brasilsat, ou mais formalmente denominado de Brasilsat A1. O satélite foi fabricado pela empresa SparAerospace Ltd., do Canadá. Com uma associação de dezenas de estações terrestres de recepção e transmissão de microondas, o Brasilsat A1 se destinava a fornecer serviços de telefonia, televisão, radiodifusão e transmissão de dados para todo o país.No ano seguinte, em 1986, foi lançado o Brasilsat A2, um satélite idêntico ao primeiro, com condições de atender também a usuários da América do Sul.Aproximando-se do final da vida útil dos satélites da primeira geração, em 1994 foi posto em órbita o Brasilsat B1 e, no ano seguinte, o Brasilsat B2, com alguns canais destinados aos países do Mercosul. Esses novos satélites de comunicação eram maiores e mais poderosos que os satélites da geração anterior.Em fevereiro de 1998, ocorreu o lançamento do satélite Brasilsat B3, com o qual algumas cidades da Amazônia, que ainda não tinham comunicação via satélite, ficaram conectadas ao Brasil e ao mundo.Porém, em 29 de julho de 1998, a empresa Embratel foi privatizada e, em 2000, a área de satélites da Embratel transformou-se numa subsidiária denominada Star One, e esta estabeleceu uma jointventure com a SociétéEuropéennedesSatellitesses-Global. O satélite Brasilsat B4 foi lançado em 17 de Agosto de 2000.Atualmente a Embratel conta com uma frota de cinco satélites de comunicações em órbita, em suas respectivas áreas geoestacionária, a 36.000 km de altitude, Estão estas localizados nas longitudes de: 75 graus oeste , 65 graus oeste e 70 graus oeste, para comunicações domésticas e internacionais, que apresentam uma alta taxa de utilização.

51. www.fisicaatual.com.brStarOneJá em 14 de novembro de 2007 foi lançado o satélite StarOne C1 que já se encontra na sua posição final, substituiria originalmente o Brasilsat B2.Em 18 de abril de 2008 A Star One lançou o StarOne C2. Estes satélites fazem parte da estratégia de renovação da frota de satélites da Star One, e substituirão os satélites Brasilsat B3,Brasilsat B4 e B2, que se aproximam do final de sua vida útil..O satélite StarOne C12 está sobre o oceano Atlântico, na posição 37,5 graus oeste, permitindo comunicações intercontinentais entre as Américas, Europa e África.Pela atual estratégia da Star One, a denominação Brasilsat deverá desaparecer e entrar em seu lugar somente o termo Star One.

52. SISTEMA DE POSICIONAMENTO GLOBAL (GPS)www.fisicaatual.com.brO segmento espacial é constituído por 24 satélites em órbita a 20.200 km de altitude. Cada satélite move-se, acima da superfície da Terra, numa velocidade de 14 400 km/h, completando uma órbita a cada 12 horas. As órbitas são arranjadas para que cada satélite repita a mesma trajetória uma vez a cada 24 horas. Assim, em qualquer ponto da Terra, num dado momento, é possível obter informações de no mínimo quatro satélites. Já o segmento controle é composto por uma estação de controle mestre (GPS Master Control Station), localizada na base da Força Aérea Americana, no Colorado, e quatro outras estações de monitoramento, localizadas em torno da Terra (Havaí, Nova Zelândia, Índia e no meio do Atlântico). Estas estações monitoram e controlam os sistemas dos satélites GPS, acompanhando suas rotas, velocidades e localizações. As estações transmitem dados para os satélites em órbita, que, por sua vez, os retransmitem de volta à Terra para uso nos receptores GPS 24 SATÉLITES EM 6 PLANOS DE ÓRBITA.