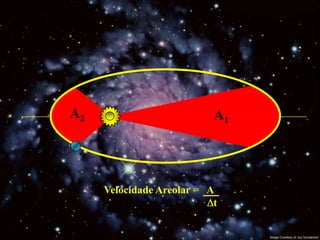
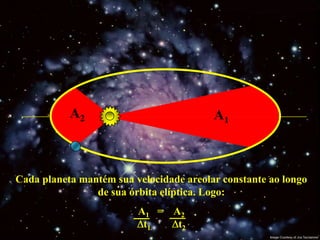
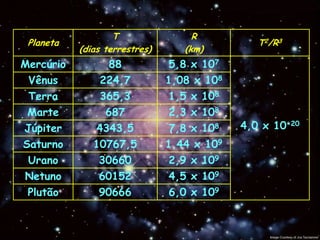
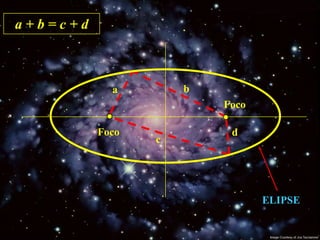
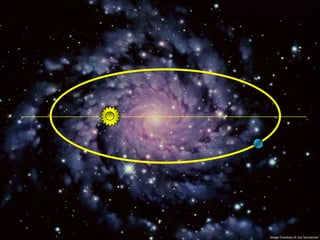
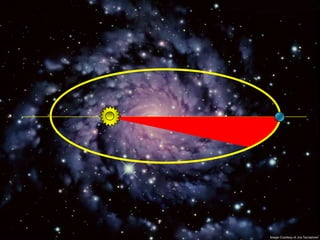
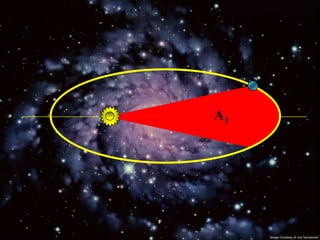
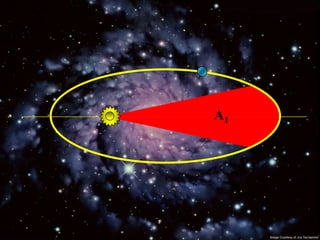
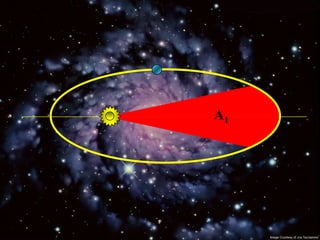
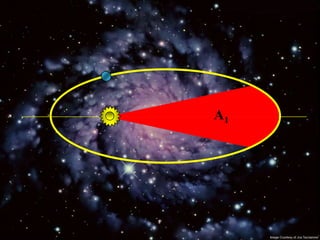
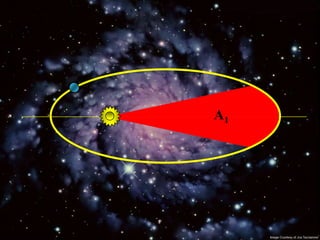
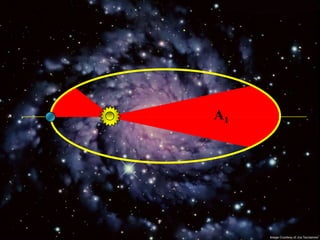
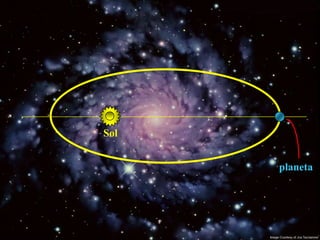
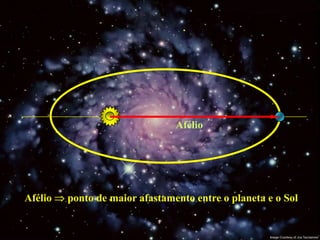
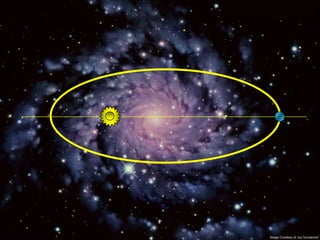
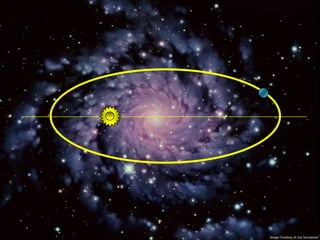
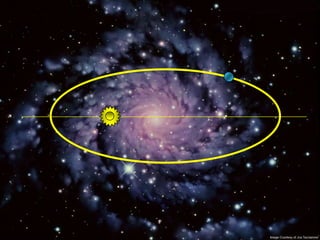
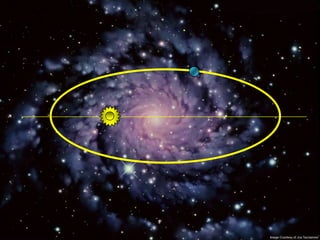
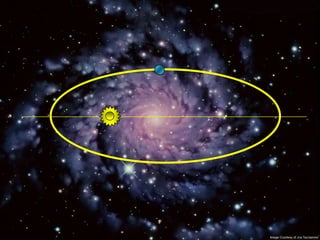
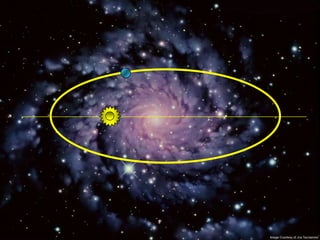
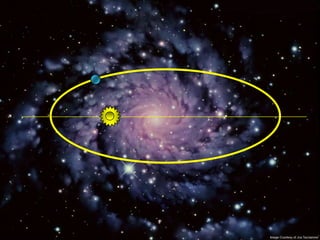
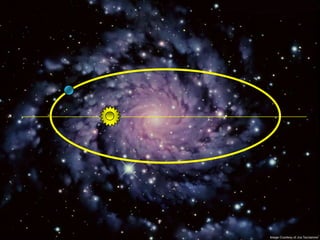
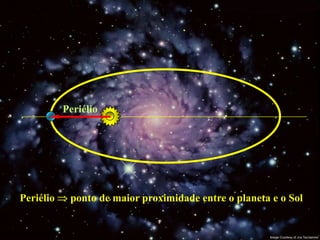
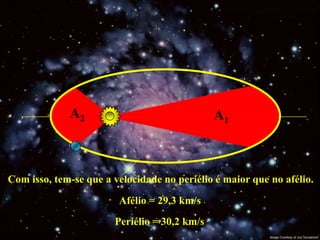
1) Johannes Kepler descobriu três leis que explicam os movimentos dos planetas em torno do Sol. 2) Suas leis mostraram que as órbitas planetárias são elipses com o Sol em um dos focos. 3) Isaac Newton explicou que a força gravitacional do Sol é responsável por fazer os planetas se movimentarem de acordo com as leis de Kepler.

1. LEIS
DE
KEPLER

2. Os primeiros a descreverem sistemas
planetários explicando os movimentos
de corpos celestes foram os gregos.
O mais famoso sistema planetário grego
foi o de Cláudio Ptolomeu (100-170), que
considerava a Terra como o centro do
Universo (sistema geocêntrico).
Segundo esse sistema, cada planeta
descrevia uma órbita circular cujo centro
descreveria outra órbita circular em torno da
Terra.

3. Nicolau Copérnico (1473-1543), astrônomo
polonês, criou uma nova concepção de
Universo, considerando o Sol como seu
centro (sistema heliocêntrico).
Segundo esse sistema, cada planeta,
inclusive a Terra, descrevia uma órbita
circular em torno do Sol.
Entretanto, o modelo de Copérnico não foi
aceito pelo astrônomo dinamarquês Tycho
Brahe (1546-1601), segundo o qual o Sol
giraria em torno da Terra e os planetas em
torno do Sol.

4. Ao morrer, Brahe cedeu suas observações a
seu discípulo Johannes Kepler (1571-1630),
que tentou, em vão, explicar o movimento
dos astros por meio das mais variadas
figuras geométricas.
Baseado no heliocentrismo, em sua
intuição e após inúmeras tentativas, ele
chegou à conclusão de que os planetas
seguiam uma órbita elíptica em torno do
Sol e, após anos de estudo, enunciou três
leis.

5. 1.ª LEI DE KEPLER
(LEI DAS ÓRBITAS)
“As órbitas dos planetas em torno do Sol são
elipses nas quais ele ocupa um dos focos.”
Numa elipse existem dois focos e a soma das
distâncias aos focos é constante.

6. a+b=c+d
a b
Foco
Foco d
c
ELIPSE

7. 2.ª LEI DE KEPLER
(LEI DAS ÁREAS)
“A área descrita pelo raio vetor de um planeta
(linha imaginária que liga o planeta ao Sol) é
diretamente proporcional ao tempo gasto
para descrevê-la.”
Velocidade Areolar velocidade com que as áreas
Afélio são descritas.

10. A1

11. A1

12. A1

13. A1

14. A1

15. A1

16. A2 A1
Velocidade Areolar = A
t

17. A2 A1
Cada planeta mantém sua velocidade areolar constante ao longo
de sua órbita elíptica. Logo:
A1 = A2
t1 t2

18. Sol
planeta

19. Afélio
Afélio ponto de maior afastamento entre o planeta e o Sol

28. Periélio
Periélio ponto de maior proximidade entre o planeta e o Sol

29. A2 A1
Com isso, tem-se que a velocidade no periélio é maior que no afélio.
Afélio = 29,3 km/s
Periélio = 30,2 km/s

30. 3.ª LEI DE KEPLER
(LEI DOS PERÍODOS)
“O quadrado do período da revolução de
um planeta em torno do Sol é diretamente
proporcional ao cubo do raio médio de sua
elipse orbital.”
Raio Médio média aritmética entre as distâncias
máxima e mínima do planeta ao Sol.
T2 = K
R3

31. T R
Planeta T2/R3
(dias terrestres) (km)
Mercúrio 88 5,8 x 107
Vênus 224,7 1,08 x 108
Terra 365,3 1,5 x 108
Marte 687 2,3 x 108
Júpiter 4343,5 7,8 x 108 4,0 x 10-20
Saturno 10767,5 1,44 x 109
Urano 30660 2,9 x 109
Netuno 60152 4,5 x 109
Plutão 90666 6,0 x 109

32. As Leis de Kepler dão uma visão
cinemática do sistema planetário.
Do ponto de vista dinâmico, que tipo de
força o Sol exerce sobre os planetas,
obrigando-os a se moverem de acordo
com as leis que Kepler descobrira?
A resposta foi dada por
Isaac Newton (1642-1727):
FORÇA GRAVITACIONAL!!!!

33. LEI DA GRAVITAÇÃO UNIVERSAL
“Dois pontos materiais se atraem
mutuamente com forças que têm a direção da
reta que os une e cujas intensidades são
diretamente proporcionais ao produto de
suas massas e inversamente proporcionais
ao quadrado da distância que os separa.”
F = G . m1 . m2
d2

34. G = constante de gravitação universal = 6,67 x 10-11 (SI)
m1 F F m2
d

35. Ainda de acordo com as Leis da Gravitação Universal:
Devido a sua enorme massa, o Sol tende a atrair
os planetas em sua direção
Quanto mais próximo do Sol, maior a velocidade
do planeta para que possa escapar do campo de
atração gravitacional do Sol
A densidade de um planeta influencia na sua
velocidade de rotação
(quanto mais denso, mais lento)