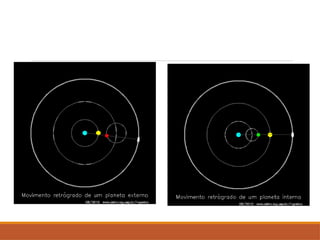
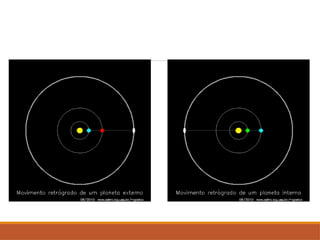
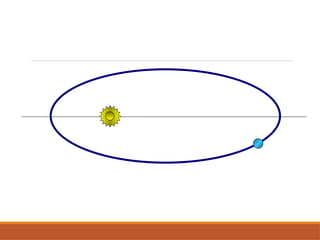
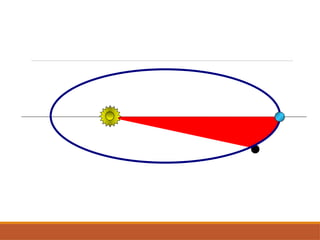
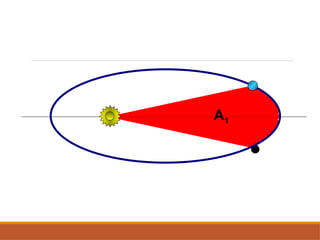
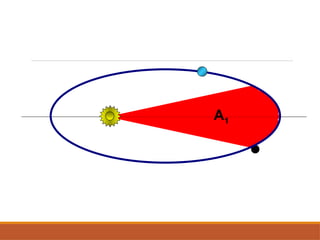
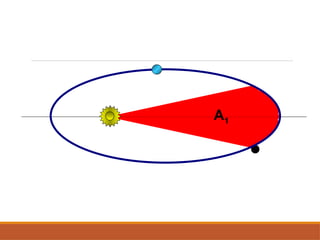
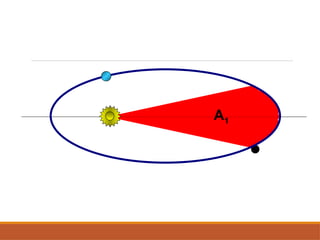
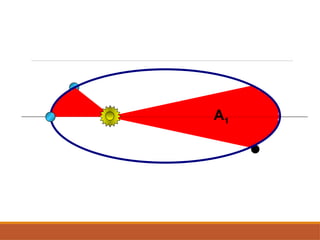
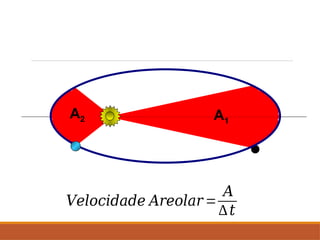
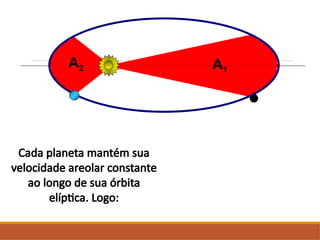
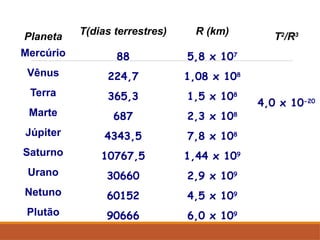
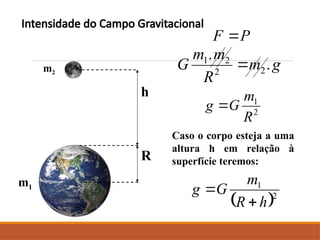
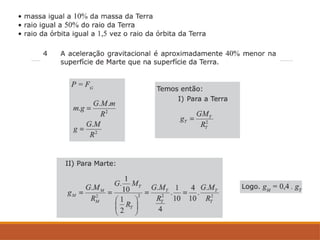
O documento discute a evolução do entendimento sobre sistemas planetários, desde a visão geocêntrica de Ptolomeu até o sistema heliocêntrico de Copérnico e as leis de Kepler. Kepler, baseado nas observações de Tycho Brahe, formulou três leis que descrevem o movimento dos planetas em órbitas elípticas e as relações entre seus períodos e distâncias ao sol. Além disso, menciona a lei da gravitação universal de Newton e apresenta conceitos sobre como ondas gravitacionais afetam o espaço-tempo.