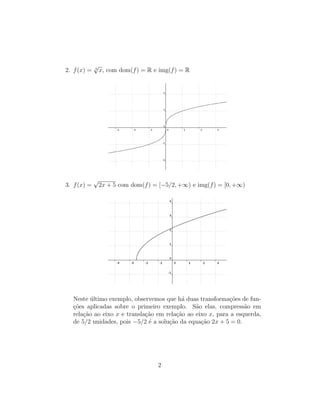
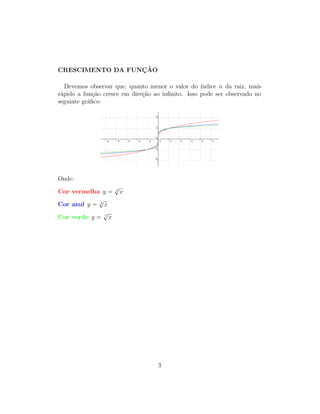
O documento define e discute funções raiz, que podem ser expressas na forma f(x) = n√g(x). O domínio depende de n ser ímpar ou par. Exemplos incluem f(x) = √x e f(x) = √2x + 5. Quanto menor o índice n, mais rápido a função cresce para infinito, como mostrado no gráfico.

1. FUNC¸ ˜OES RA´IZES
Prof. Dr. Carlos A. P. Campani
DEFINIC¸ ˜AO E DOM´INIO
Uma fun¸c˜ao ra´ız ´e toda fun¸c˜ao que pode ser expressa na forma
f(x) = n
g(x)
para algum n inteiro, n ≥ 2, e para qualquer fun¸c˜ao g(x).
O dom´ınio da fun¸c˜ao raiz deve considerar dois casos:
• Se n ´e ´ımpar, o dom´ınio da fun¸c˜ao ´e o dom´ınio de g(x)
• Se n ´e par, o dom´ınio da fun¸c˜ao ´e dom(f) = {x ∈ R|x ∈ dom(g) ∧
g(x) ≥ 0}, pois n˜ao existe raiz de ´ındice par de n´umero negativo
Quanto `a imagem da f, podemos afirmar que se n ´e par, os valores da
fun¸c˜ao ser˜ao sempre positivos.
EXEMPLOS E GR´AFICO DA FUNC¸ ˜AO
1. f(x) =
√
x, com dom(f) = [0, +∞) e img(f) = [0, +∞)
1

2. 2. f(x) = 3
√
x, com dom(f) = R e img(f) = R
3. f(x) =
√
2x + 5 com dom(f) = [−5/2, +∞) e img(f) = [0, +∞)
Neste ´ultimo exemplo, observemos que h´a duas transforma¸c˜oes de fun-
¸c˜oes aplicadas sobre o primeiro exemplo. S˜ao elas, compress˜ao em
rela¸c˜ao ao eixo x e transla¸c˜ao em rela¸c˜ao ao eixo x, para a esquerda,
de 5/2 unidades, pois −5/2 ´e a solu¸c˜ao da equa¸c˜ao 2x + 5 = 0.
2

3. CRESCIMENTO DA FUNC¸ ˜AO
Devemos observar que, quanto menor o valor do ´ındice n da raiz, mais
r´apido a fun¸c˜ao cresce em dire¸c˜ao ao infinito. Isso pode ser observado no
seguinte gr´afico:
Onde:
Cor vermelha y = 3
√
x
Cor azul y = 5
√
x
Cor verde y = 7
√
x
3