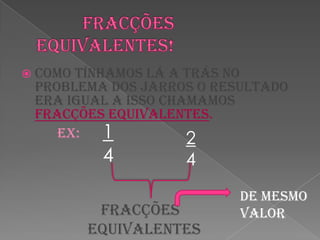
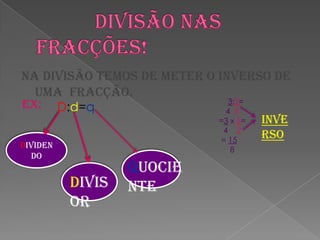
Este documento explica os conceitos básicos de frações, incluindo a definição de numerador e denominador, comparação de frações, operações com frações (multiplicação, subtração, divisão e soma) e fracções equivalentes. O documento fornece exemplos de cada um desses tópicos para ilustrar como aplicar os conceitos.

1. Fracções! Trabalho realizado por: Beatriz Lemos nª4 6ªD Disciplina: Matemática Professor David pereira

2. As fracções aNumerador b Denominador 7Parte pintada 10 Parte não pintada

3. Comparação de números racionais Quando o numerador e o denominador são iguais representa a unidade.Ex: 6 1 6Quando o numerador é maior que o denominador representa um número maior que 1. Ex: 10 1 6

4. Comparação de números racionais Quando o numerador é menor que o denominador representa um número menor que 1.Ex: 4 1 10

5. Como saber qual o maior e o menor?! Duas fracções com o mesmo numerador a fracção maior é a que tem o denominador menor .Ex: 66 5 12

6. Como saber qual o maior e o menor?! Se tivermos duas fracções com o mesmo denominador, a maior é a do numerador maiorEx: 63 5 5

7. Fracções equivalentes!

8. Se eu tiver 2 jarros de sumo e repartir um ao meio e o outro em 4 partes iguais será que fica igual? R: Sim, ficará igual porque um meio representa dois quartos 1 4 Fracções equivalentes! 1 2 1 4 1 jarro 1 jarro 1 4 2 4 1 2 1 4 1 1 2 2 2 4

9. Fracções equivalentes! Como tínhamos lá a trás no problema dos jarros o resultado era igual a isso chamamos Fracções equivalentes. 1 4 Ex: 2 4 De mesmo valor Fracções equivalentes

10. Fracções equivalentes Por exemplo se eu tiver 3 pizzas, e divido uma em 4 partes iguais, outra 8 partes iguais e outra em 16 partes iguais. Será que são equivalentes? 1 pizza 1 pizza 1 pizza

11. Fracções equivalentes Tínhamos as 3 pizzas, agora falta ver se são equivalentes. 1 4 1 16 1 8 R: São equivalentes porque: 4+4=8 8+8=16 Também podíamos fazer por contas de vezes, assim: 4x2=8 8x2=16 16x2=32

12. Multiplicação, subtracção, divisão e soma nas fracções!

13. Multiplicação nas fracções! Na multiplicação primeiro fazemos a resolução dos numeradores e depois dos denominadores. Ex: 3x 1 = 3 2 2 1 + 1+ 1 = 3 2 2 2 2 É o mesmo que Produto dos numeradores. Produto dos denominadores.

14. Subtracção nas fracções. Na subtracção temos de ter os denominadores iguais. Metemos o x2 em cima do 5 e do dois por uma simples razão, e essa é a seguinte: como para fazer a subtracção temos de ter os denominadores iguais e aqui não tínhamos tivemos de os meter. Tens de multiplicar sempre o de cima (numerador) e o de baixo (numerador). É muito simples! x2 25-18= 2x2 4 = 50-18 = 4 4 = 32 4 Ex:

15. Divisão nas fracções! Na divisão temos de meter o inverso de uma fracção. Ex: 3:2= 4 5 =3 x 5= 4 2 = 15 8 D:d=q inverso Dividendo quociente divisor

16. Soma nas fracções! Na soma para fazer a operação temos de ter os denominador iguais tal como na subtracção. Ex: 1x4+7+1= 2x48 8 =4+7+1= 8 8 8 =11+ 1= 8 8 =12 8

17. Todas as 4 operações 2 2+1x 2:1-2-1 = 2 2 3 3 =4+1x2:1-2-1 = 2 2 3 3 =4+1x2:1-1 = 1 2 1 2 3 =4+1:1-1= 1 2 3 =4+1x2-1 = 3 =4+2-1 = 3 = 6x3-1=17 1x3 3 3

18. Conclusão… Eu não entendia nada de fracções, então decidi fazer este trabalho. Com isto tudo agora já as consigo resolver melhor! Espero que gostem e que entendam.

19. FIM