O documento discute como construir triângulos a partir de diferentes informações sobre seus lados e ângulos. Ele fornece exemplos de como construir triângulos sabendo: 1) o comprimento dos três lados, 2) o comprimento de dois lados e o ângulo entre eles, e 3) o comprimento de um lado e a medida de dois ângulos adjacentes. O documento também lista os três métodos para construir triângulos.

1. Construção de triângulos

2. 1.º Vamos rever a “Desigualdade Triangular”
   DEFABC    DEFABC    DEFABC    DEFABC 
Num triângulo, qualquer lado é menor
que a soma dos outros dois.

3. Construção de triângulos
Material necessário:
Transferidor
Régua
Compasso
Borracha e lápis

4. Antes de construíres um triângulo, conhecendo a medida dos
três lados, tens de verificar se…
É possível construir o triângulo!?
Construção de um triângulo sabendo o comprimento dos três lados
Verifica pela desigualdade triangular…
Com estes
comprimentos
NÃO é possível construir
um triangulo

5. Também NÃO é possível
construir um triangulo,
com estas medidas

6. É POSSÍVEL construir
um triangulo,
com estas medidas

7.    DEFABC    DEFABC    DEFABC    DEFABC 
Construção de um triângulo sabendo o comprimento de
dois lados e a amplitude do ângulo por eles formado

8. 1.º EXEMPLO
DADA A MEDIDA DOS 3 LADOS DO TRIÂNGULO
Constrói um triângulo [ABC] tal que: [AB] = 3cm; [BC] = 6cm; [AC] = 4cm.
• Com o auxílio de uma régua graduada, traça um dos lados do
triângulo, por exemplo, [BC].
• Sabes que [AB] = 3 cm. Com o compasso, traça um arco de
circunferência com centro em B e raio = 3 cm.
• Sabes que [AC] = 4 cm. Com o compasso, traça um arco de
circunferência com centro em C e raio = 4 cm até cruzar o outro arco.
• Um dos dois pontos de intersecção dos arcos de circunferência
define o vértice A.
• Com a régua une A aos vértices B e C.• Também podias construir o triângulo ao contrário, ou seja, unir A’
aos vértices B e C.
B C
A
A’

9.    DEFABC    DEFABC    DEFABC    DEFABC 
5 cm
6 cm
Agora experimenta tu…
__
AB = 10 cm
BC = 5 cm
__
__
AC = 6 cm
A B
C
10 cm
Por exemplo

10.    DEFABC    DEFABC    DEFABC    DEFABC 
Construção de um triângulo sabendo o comprimento de
dois lados e a amplitude do ângulo por eles formado

11. B
C
A
2.º EXEMPLO
DADA A MEDIDA DE 2 LADOS E 1 ÂNGULO DO TRIÂNGULO
Constrói um triângulo [ABC] tal que: [BC] = 4cm; [AB] = 6cm; CÂB = 40º.
• Com o auxílio de uma régua graduada, traça um dos lados do
triângulo, por exemplo, [AB].
• Com o transferidor marca o ângulo CÂB de amplitude 40º e vértice
em A.
• Traça a semi-recta com origem em A e que passa pela marca que
assinalaste.
• Com o compasso, ou com a régua graduada, marca o ponto C tal que
[CA] = 4 cm.
• Com a régua, une o ponto C ao ponto B.• Apaga as linhas de construção e está o triângulo traçado.

12.    DEFABC    DEFABC    DEFABC    DEFABC 
45º
6 cm
__
AB = 10 cm
B = 45º^
__
BC = 6 cm
10 cm
A B
C
Por exemplo
Agora experimenta tu…

13. Construção de um triângulo dado o comprimento de um
dos lados e a amplitude dos ângulos adjacentes
   DEFABC    DEFABC    DEFABC    DEFABC 

14. 3.º EXEMPLO
DADA A MEDIDA DE 1 LADO E 2 ÂNGULOS DO TRIÂNGULO
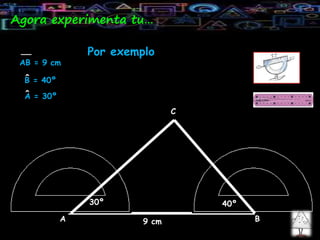
Constrói um triângulo [ABC] tal que: [AC] = 6cm; CÂB = 40º; BĈA = 30º.
• Com o auxílio de uma régua graduada, traça o lado [AC] do triângulo.• Com transferidor marca o ângulo CÂB de amplitude 40º e vértice em
A.
• Traça a semi-recta com origem em A e que passe pela marca que
assinalaste.
• Com transferidor marca o ângulo BĈA de amplitude 30º (150º) e
vértice em C.
• Traça a semi-recta com origem em C e que passe pela marca que
assinalaste.
• O ponto de intersecção das duas linhas anteriores define o vértice B
do triângulo.
A C
B
• Apaga as linhas de construção e está o triângulo traçado.

15.    DEFABC    DEFABC    DEFABC    DEFABC 
40º30º
A B
C
__
AB = 9 cm
B = 40º^
A = 30º^
9 cm
Por exemplo
Agora experimenta tu…

16. Podemos construir triângulos sabendo:
   DEFABC    DEFABC    DEFABC    DEFABC 
Um comprimento de um lado e a amplitude
dos dois ângulos adjacentes.
O comprimento de dois lados e a
amplitude do ângulo por eles formado.
O comprimento dos três lados.
Conclusões