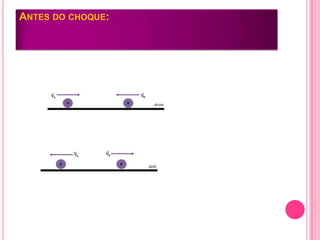
O documento discute colisões mecânicas entre dois corpos, definindo tipos de colisão como perfeitamente elástica, parcialmente elástica e inelástica. Explica a velocidade de aproximação e afastamento e o coeficiente de restituição, ilustrando com dois exercícios resolvidos sobre colisões perfeitamente elásticas.

1. COLISÕES OU CHOQUES MECÂNICOS
PROF : ADRIANNE MENDONÇA

2. COLISÕES
 Imagine uma partida de sinuca na qual uma bola é atirada
contra outras bolas gerando colisões. Nessas colisões podem
ocorrer diversas situações, como, por exemplo, uma bola
para e outra segue em
movimento, uma bola segue atrás da outra, uma bola segue
adiante e outra volta.
Vamos agora analisar as colisões entre dois corpos, mas
vamos dar maior atenção às colisões que ocorrem numa
única direção, ou seja, unidirecionais.
Colisões unidirecionais frontais

 Consideremos uma colisão central e frontal de dois corpos, A
e B, com movimentos na direção horizontal e apoiados numa
superfície plana e horizontal.

3. ANTES DO CHOQUE:

4. NOTE !!!
 Durante uma colisão de dois corpos, as forças
externas são desprezadas se comparadas às
internas, portanto, o sistema pode ser sempre
considerado mecanicamente isolado:

5. OBS.
 As velocidades devem ser colocadas na equação
dada com seus respectivos sinais. No nosso
exemplo, se a orientação da trajetória for para a
direita, temos VA > 0, VB < 0, V’A > 0 e V’B > 0.
 Coeficiente de restituição
 Antes do choque (colisão), os corpos A e B se
aproximam com velocidade Vap(velocidade de
aproximação).
 Vap = VA - VB
 Após o choque, os corpos A e B se afastam com
velocidade Vaf (velocidade de afastamento).

6. NOTE !!!
 Vaf = V’B – V’A
 O coeficiente de restituição (e) de um choque é
definido pela razão entre as velocidades de
afastamento e velocidade de aproximação.
 Tipos de choque
 No choque entre dois corpos podem ocorrer perdas
de energia em virtude do aquecimento, da
deformação e do som provocados pelo impacto,
porém, jamais haverá ganho de energia.

7. ILUSTRANDO ...

8. IMPORTANTE !!!
 Portanto, o módulo da velocidade de afastamento
deve ser menor ou, no máximo, igual ao módulo da
velocidade de aproximação.
 Como a velocidade de afastamento (Vaf) apresenta
módulo menor ou igual ao módulo da velocidade de
aproximação (Vap), a razão entre elas determina um
coeficiente de restituição compreendido entre zero
e um.
 Choque perfeitamente elástico
 É o tipo de choque que ocorre quando, após a
colisão, os corpos seguem separados (velocidade
diferentes) e o sistema não perde energia cinética.

9. CHOQUE PARCIALMENTE ELÁSTICO
 É o tipo de choque que ocorre quando, após a
colisão, os corpos seguem separados (velocidade
diferentes), tendo o sistema uma perda de energia
cinética.

10. CHOQUE INELÁSTICO
 É o tipo de choque que ocorre quando, após a
colisão, os corpos seguem juntos (com a mesma
velocidade).

11. EXERCÍCIO 1
 Dois corpos de massas iguais a 2,0 kg e 3,0 kg
movem-se em sentido oposto e na mesma direção
com velocidades respectivamente iguais a 6,0 m/s
e 4,0 m/s. Considerando a colisão perfeitamente
elástica, determine a velocidades dos corpos após
a colisão.

12. SOLUÇÃO
 Qantes = Qdepois, logo 2.4 + 6.1 = 2.Va + 6.Vb, logo
6Vb+2Va=14 (I)
Choque perfeitamente elástico = coeficiente de
restituição (e) = 1:
e=1, logo (Va+Vb)/(4+1) = 1, logo Va+Vb=5, logo Vb=5-
Va. Substituindo isso na equação (I) fica:
6(5-Va)+2Va=14, logo 30-6Va+2Va=14, logo -4Va= -16,
logo Va= 4m/s e assim Vb= 1m/s
Resp: as velocidades têm o mesmo módulo de antes, o
que já é esperado numa colisão perfeitamente elástica.

13. EXERCÍCIO 2
 Dois corpos A e B, de massa respectivamente
iguais a 2 kg e 6 kg, movimentam-se sobre uma
mesma trajetória retilínea, no mesmo sentido com
velocidades vA = 4 m/s e vB = 1 m/s, onde o atrito
é desprezível. Sabendo-se que os corpos realizam
uma colisão perfeitamente elástica, determine suas
velocidades após o choque.

14. SOLUÇÃO
 Qantes=Qdepois, logo 2.6 - 3.4 = -2.V+3.v, logo -
2V+3v=0, logo 2V= 3v, logo V= 1,5v (I)
Choque perfeitamente elástico = coeficiente de
restituição (e) = 1:
e=1, logo (-V+v)/(6-4) = 1, logo -V+v=2, logo v=2+V.
Substituindo o valor da equação (I) aqui fica:
v=2+1,5v, logo -0,5v=2, logo v= -4m/s e assim V= -6m/s
Resp: as velocidades têm o mesmo módulo de antes, o
que já é esperado numa colisão perfeitamente elástica.