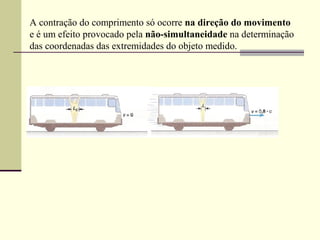
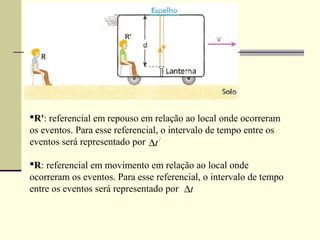
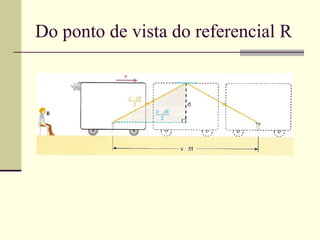
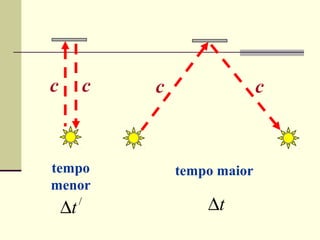
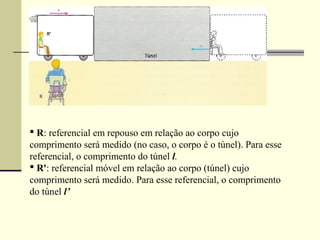
1) O documento discute os conceitos de relatividade restrita, introduzindo os postulados da teoria, como a constância da velocidade da luz e o princípio da relatividade. 2) A teoria da relatividade restrita prevê que grandezas como comprimento, tempo e massa são relativas ao referencial inercial de observação. Isso leva a efeitos como a dilatação do tempo e contração do espaço. 3) A teoria foi fundamental para explicar fenômenos como a chegada de partículas cósmicas à superfí

1. Relatividade Restrita

2. Introdução
 As grandezas comprimento, tempo e massa, entretanto,
sempre foram tratadas como absolutas, isto é,
independentes do referencial em que são medidas. Se
alguém afirmar que o comprimento de uma ponte, o
tempo de duração de uma aula e a massa de uma pessoa
dependem do referencial, você certamente achará
absurdas essas afirmações. Entretanto, como veremos
nesta breve exposição, comprimento, massa e tempo,
grandezas consideradas absolutas na Mecânica clássica,
também são grandezas relativas! A relatividade dessas
grandezas, porém, só fica evidenciada quando estudamos
situações em que as velocidades são muito altas, isto é,
não-desprezíveis em comparação com a velocidade da
luz no vácuo, que é de 300000 km/s, aproximadamente.

3.  O motivo da nossa perplexidade diante do caráter relativo
do comprimento, do tempo e da massa é estarmos
habituados a situações em que as velocidades são
insignificantes em comparação com a da luz. Mesmo a
velocidade de 2000 km/h de um avião supersônico e a
velocidade de 30 km/s da Terra em seu movimento de
translação ao redor do Sol são desprezíveis em
comparação com 300000 km/s.

4. Albert Einstein (1879-1955)
Albert Einstein, físico alemão
naturalizado americano. Premiado
com o Nobel de Física em 1921, é
famoso por ser autor das teorias
especial e geral da relatividade e
por suas idéias sobre a natureza
corpuscular da luz. É
provavelmente o físico mais
conhecido do século XX.

5. Postulados
Essa teoria fundamentou-se em dois postulados.
 • Princípio da relatividade: As leis da Física são as
mesmas, expressas por equações que têm a mesma forma,
em qualquer referencial inercial. Não existe um referencial
inercial privilegiado.
 • Princípio da constância da velocidade da luz: a
velocidade da luz no vácuo vale c = 300.000 km/s em
todos os referenciais inerciais, independentemente do
movimento da fonte em relação ao observador.

6. Se ligue!!!
 Note que o segundo postulado contraria radicalmente a maneira
newtoniana de compor velocidades. Para confirmar isso, considere
uma nave em repouso em relação às estrelas e recebendo a luz emitida
por uma lanterna, como ilustra a figura a seguir.
 Imagine, agora, que a nave entre em movimento retilíneo e uniforme
para a direita, a 100000 km/s. Se a composição de velocidades da
Mecânica clássica continuasse valendo, a velocidade da luz emitida
pela lanterna seria, em relação à nave, de 400000 km/s. Entretanto, por
mais absurdo que pareça, essa velocidade continua igual a 300000
km/s!

7. Conseqüências da Relatividade de Einstein
 Dilatação do tempo
 Contração do espaço

8. Dilatação do Tempo

9. R': referencial em repouso em relação ao local onde ocorreram
os eventos. Para esse referencial, o intervalo de tempo entre os
eventos será representado por ∆t /
R: referencial em movimento em relação ao local onde
ocorreram os eventos. Para esse referencial, o intervalo de tempo
entre os eventos será representado por ∆t

10. Do ponto de vista do referencial R'
∆s
Como v = , temos :
∆t
2d 2d
c = / ⇒ ∆t = /
∆t c

11. Do ponto de vista do referencial R

12. 2 2
 c ⋅ ∆t   v ⋅ ∆t 
 = d +  ⇒
2

 2   2 
2
c ⋅ ∆t
2 2
v ⋅ ∆t
2
⇒ =d +2
⇒
4 4
⇒ c 2 ⋅ ∆t 2 = 4d 2 + v 2 ⋅ ∆t 2 ⇒
⇒ (c 2 − v 2 )∆t 2 = 4d 2 ⇒
4d 2 4d 2
⇒ ∆t 2 = 2 2 = ⇒
(c − v ) 2 v 
2
c 1 − 2 
 c 
 
2d ∆t /
⇒ ∆t = ⇒ ∆t =
2
v v2
c 1− 2 1− 2
c c

13. c c c c
tempo tempo maior
menor
∆t / ∆t

14. ∆t /
∆t = Fator de Lorentz
2
v
1− 2 1
c γ=
v2
1− 2
∆t = γ ⋅ ∆t / c
Note que, para R', o tempo passa mais devagar.
Qualquer processo físico, reação química ou processo
biológico que ocorre dentro do vagão é mais lento
para R' do que para R. Incluem-se nesse caso os batimentos
cardíacos e a rapidez com que o mecanismo de um relógio opera.

15. Paradoxo do Gêmeos
Consideremos uma experiência controlada que envolva dois
gêmeos de 20 anos, Eliandro e Leandro. Eliandro, o gêmeo mais
aventureiro, mais mais , etc. empreende uma jornada até uma
estrela, a 30 anos-luz da Terra. A sua astronave é capaz de acelera
até velocidade próxima da velocidade da luz. Depois de chegar à
estrela, Eliandro sente muitas saudades, e retorna imediatamente à
Terra, com a mesma velocidade elevada. No seu retorno, fica
admirado pelas muitas mudanças. Antigas cidades expandiram-se,
novas apareceram. Leandro, envelheceu cerca de 80 anos e
Eliandro, porém, envelheceu apenas 10 anos e ainda continuava
bonitão. Isso em virtude de os seus processos corporais se terem
alentecido durante a viagem no espaço.

16. Um dos fatos que confirmam a
Teoria da Relatividade Restrita
Raios cósmicos incidentes nas altas camadas da atmosfera produzem
partículas instáveis, denominadas mésons µ (ou múons). Sabe-se que
a vida média de um méson µ, medida em um referencial em repouso
em relação a ele, é de 2,2 µs, aproximadamente. Após esse
curtíssimo intervalo de tempo, o méson µ desintegra-se, dando
origem a outras partículas (um elétron, um antineutrino do elétron e
um neutrino do múon). Muitos múons produzidos na alta atmosfera
movem-se a uma velocidade igual a 0,998 c, aproximadamente.
Vamos calcular a distância que poderiam percorrer antes de se
desintegrarem:
−6
∆s = v ⋅ t = (0,998 ⋅ 3 ⋅10 ) ⋅ (2,2 ⋅10 )
8
∆s ≅ 660m

17. Como a altitude da região em que são produzidas é muito maior que
660 m, essas partículas não deveriam chegar à superfície da Terra.
No entanto, chegam em abundância. Note que estamos diante de
um problema concreto. Como a velocidade dos mésons é muito
alta, os efeitos relativísticos não podem ser ignorados, e o problema
deve ser resolvido pela Teoria da Relatividade.

18. ∆t / 2,2 ⋅10 −6
∆t = = ⇒ ∆t ≅ 35µs
2 2
v (0,998c)
1− 2 1−
c c2
Então, em relação a R, o méson, ainda " vivo", é capaz de
percorrer uma distância l dada por :
l = v ⋅ ∆t = (0,998 ⋅ 3 ⋅108 ) ⋅ (35 ⋅10 −6 ) ⇒ l ≅ 10500m
Dessa forma, fica explicado por que os mésons
conseguem chegar à superfície da Terra.

19. Exemplo 01
Um foguete parte da Terra com velocidade v= 0,8c, em relação à Terra,
transportando um astronauta. Em relação ao foguete, a viagem dura 3 anos.
Quanto durou a viagem do astronauta em relação a um observador na
Terra?
∆t = ? → ∆t / = 3anos
∆t / 3
∆t = ⇒ ∆t =
v2 (0,8c) 2
1− 2 1−
c c2
3
∆t = ⇒ ∆t = 5anos
0,6

20. Contração do Espaço
Se um observador mede o comprimento de um objeto que está
em movimento relativamente a ele, o valor obtido é diferente daquele
que seria encontrado se a medição fosse feita num referencial onde o
objeto estivesse em repouso, Esse efeito é conseqüência direta da
dilatação do tempo. Analisemos uma situação hipotética simples. Isso é
o que Einstein chamava de experiência mental.

21.  R: referencial em repouso em relação ao corpo cujo
comprimento será medido (no caso, o corpo é o túnel). Para esse
referencial, o comprimento do túnel l.
 R': referencial móvel em relação ao corpo (túnel) cujo
comprimento será medido. Para esse referencial, o comprimento
do túnel l’

22. Do ponto de vista do referencial R
l
v= ⇒ l = v ⋅ ∆t
∆t

23. Do ponto de vista do referencial R’
l' ∆t /
v= ⇒ l ' = v ⋅ ∆t '. Como ∆t = ,
∆t ' v 2
1− 2
c
v2
podemos escrever ∆t ' = ∆t ⋅ 1 − 2 . Então;
c
v2
l ' = v ⋅ ∆t ' ⇒ l ' = v ⋅ ∆t 1 − 2
c
Temos :
v2
l' = l 1− 2
c

24. Se o corpo em estudo estivesse dentro do vagão e fixado
nele, o referencial R, em repouso em relação ao corpo,
estaria no vagão. O referencial R', por sua vez, em movimento
em relação ao corpo, estaria no solo. Nessa situação,
a contração do comprimento do corpo ocorreria para R'.
O comprimento l' que a barra tem em relação a R' é menor que o
comprimento l que ela tem em relação a R:
l ' menor que l
v2
l' = l 1− 2
c

25. A contração do comprimento só ocorre na direção do movimento
e é um efeito provocado pela não-simultaneidade na determinação
das coordenadas das extremidades do objeto medido.

26. Exemplo 02
Considere uma barra em repouso em relação a um sistema de referência R’.
Este se movimenta em relação ao sistema de referência R com velocidade
v=08c. Seja L=1,0m o comprimento da barra medido no referencial R’.
Sabendo-se que a barra está alinhada na direção do movimento, determine o
comprimento da barra em relação ao referencial R.

27. L/ = 1,0m
v = 0,8c
L/  v2  /  (0,8c) 2 
L = =  1− 2  ⋅ L ⇒ L =  1−  ⋅1
γ  c 

 c2 

L = 0,36 = 0,60m

28. Exemplo 03
Uma nave espacial tem o comprimento de 100m, medidos por um observador
em repouso em relação à nave. Se a nave passar por um observador com
velocidade de 0,99c, qual o comprimento que este observador atribuirá à
nave?
L/ = 100m
v = 0,99c
L/  v2  /  (0,99c) 2 
L = =  1− 2  ⋅ L ⇒ L =  1−  ⋅100
γ  c 

 c2 

L= ( )
0,02 ⋅100 = 14m
Se a nave espacial passar pelo observador em repouso com a velocidade
0,01c, qual o comprimento que este observador medirá?

29. Composição de velocidades
u ' → velocidade do objeto P em relação ao vagão
v → velocidade do vagão
u → velocidade do objeto P em relação ao solo (R)
Pode - se demonstrar que a velocidade u do objeto P em relação
ao solo é dada por :
u '+v
u=
vu '
1+ 2
c

30. Exemplo 04
Uma nave move-se com velocidade 0,80 c em relação ao solo quando
lança um projétil com velocidade 0,60 c em relação a ela, como
ilustra a figura.
u '+ v 0,60c + 0,80c
u= = ⇒
vu ' 0,80c ⋅ 0,60c
1+ 2 1+
c c2
1,40c
⇒u = ⇒ u = 0,95c
1,48
Imagine que fosse possível termos v = c e
u' = c; calculem o novo valor de u.

31. Massa e Energia
Para que o princípio da conservação da quantidade de movimento
continuasse válido no domínio de colisões interratômicas (onde a velocidade
das partículas é compatível à velocidade da luz), Einstein reformulou os
conceitos de massa e energia.
m0 Massa de repouso
A massa do corpo é maior
quando em movimento do
m0 que quando em repouso.
m = γ ⋅ m0 ⇒ m =
v2
1− 2 O aumento da massa não
c significa que aumenta o
número de partículas do
corpo, e sim a inércia.

32. Massa é uma forma de Energia
E = m ⋅ c → Energia Total
2
E0 = m0 ⋅ c → Energia de repouso
2
Energia Cinética
EC = E − E0
EC = m ⋅ c − m0 ⋅ c
2 2

33. Quantidade de Movimento
Q = m⋅v
m0
Como : m = , temos :
v2
1− 2
c
m0
Q= ⋅v
v2
1− 2
c