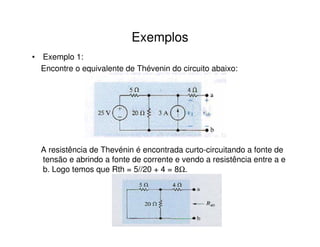
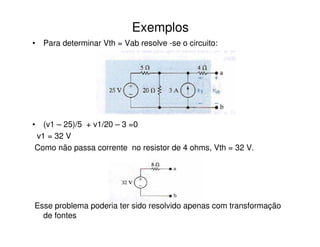
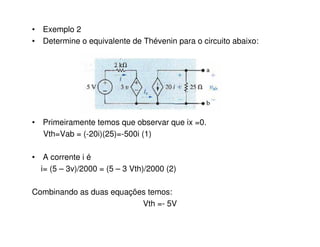
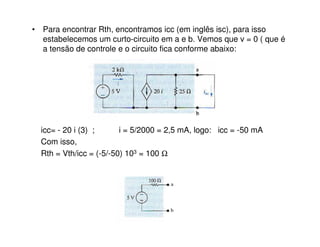
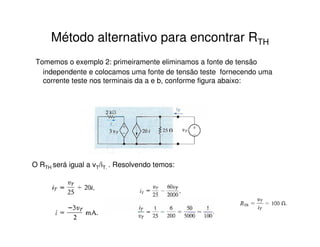
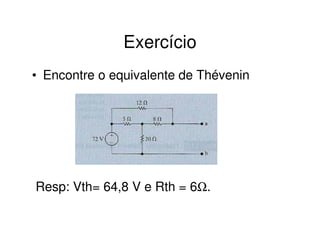
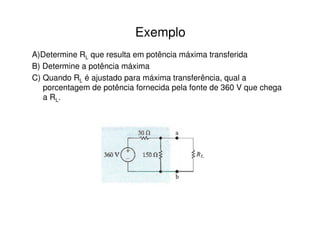
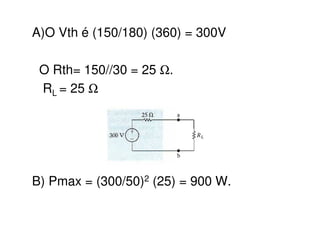
1) O documento introduz os conceitos de circuitos equivalentes de Thévenin e Norton, que permitem substituir circuitos complexos por fontes ideais em série ou paralelo com resistores. 2) Os circuitos equivalentes de Thévenin possuem uma fonte de tensão ideal em série com um resistor, enquanto os de Norton possuem uma fonte de corrente ideal em paralelo com um resistor. 3) Exemplos ilustram como calcular os parâmetros desses circuitos equivalentes a partir de circuitos originais.

1. Equivalentes de Thévenin e
Norton

2. Introdução
• Na análise muitas vezes nos interessa o
que acontece em um par específico de
terminais. Por exemplo, quando ligamos
algum equipamento a uma tomada,
estamos interessados principalmente na
tensão e na corrente nos terminais do
equipamento.

3. Definições
• Um circuito formado por fontes independentes, resistores e eventualmente fontes
vinculadas (com a restrição de serem vinculadas a variáveis do próprio circuito),
ligado por apenas dois nós a um circuito externo qualquer (que será chamado de
carga) pode ser substituído por:
– um circuito equivalente de Thévenin, constituído de uma fonte ideal de tensão em
série com um resistor linear
– A fonte de tensão deve ter tensão igual à tensão em aberto do circuito original, isto é,
a tensão que apareceria entre os nós se o segundo circuito fosse retirado. (A fonte de
corrente deve ter corrente igual à corrente em curto-circuito do circuito original, isto
é, a corrente que circularia entre os nós curto-circuitados.)
– A resistência do resistor (chamada de resistência de Thévenin), nos dois casos, é
igual à resistência do circuito original com todas as fontes independentes anuladas.
Alternativamente, a resistência de Thévenin pode ser obtida como a relação entre a
tensão em aberto e a corrente em curto-circuito do circuito original.

4. Definições
• O circuito equivalente de Norton consiste em
uma fonte de corrente independente em
paralelo com a resistência equivalente de
Norton.
• Podemos obtê-lo de um circuito equivalente de
Thévenin por uma simples transformação de
fonte.
• A corrente de Norton é igual à corrente de curto
nos terminais de interesse e a resistência é a
mesma de Thévenin.

5. Definições
• Às vezes, podemos fazer uso de apenas
transformações de fonte para obter o
circuito equivalente de Thévenin ou de
Norton.

6. Exemplos
• Exemplo 1:
Encontre o equivalente de Thévenin do circuito abaixo:
A resistência de Thevénin é encontrada curto-circuitando a fonte de
tensão e abrindo a fonte de corrente e vendo a resistência entre a e
b. Logo temos que Rth = 5//20 + 4 = 8W.

7. Exemplos
• Para determinar Vth = Vab resolve -se o circuito:
• (v1 – 25)/5 + v1/20 – 3 =0
v1 = 32 V
Como não passa corrente no resistor de 4 ohms, Vth = 32 V.
Esse problema poderia ter sido resolvido apenas com transformação
de fontes

8. • Exemplo 2
• Determine o equivalente de Thévenin para o circuito abaixo:
• Primeiramente temos que observar que ix =0.
Vth=Vab = (-20i)(25)=-500i (1)
• A corrente i é
i= (5 – 3v)/2000 = (5 – 3 Vth)/2000 (2)
Combinando as duas equações temos:
Vth =- 5V

9. • Para encontrar Rth, encontramos icc (em inglês isc), para isso
estabelecemos um curto-circuito em a e b. Vemos que v = 0 ( que é
a tensão de controle e o circuito fica conforme abaixo:
icc= - 20 i (3) ; i = 5/2000 = 2,5 mA, logo: icc = -50 mA
Com isso,
Rth = Vth/icc = (-5/-50) 103 = 100 W

10. Método alternativo para encontrar RTH
Tomemos o exemplo 2: primeiramente eliminamos a fonte de tensão
independente e colocamos uma fonte de tensão teste fornecendo uma
corrente teste nos terminais da a e b, conforme figura abaixo:
O RTH será igual a vT/iT. . Resolvendo temos:

11. Exercício
• Encontre o equivalente de Thévenin
Resp: Vth= 64,8 V e Rth = 6W.

12. Máxima transferência de potência
• Circuito que descreve a máxima transferência de potência
• O problema é determinar o valor de RL que permita a máxima
transferência de potência

13. • Deriva-se a expressão anterior em função de RL, logo
• Como queremos o máximo a derivada é igual a zero, logo:
Resolvendo temos:
Rth = RL
Essa é a condição de máxima transferência de potência

14. Assim a potência máxima é dada por:

15. Exemplo
A)Determine RL que resulta em potência máxima transferida
B) Determine a potência máxima
C) Quando RL é ajustado para máxima transferência, qual a
porcentagem de potência fornecida pela fonte de 360 V que chega
a RL.

16. A)O Vth é (150/180) (360) = 300V
O Rth= 150//30 = 25 W.
RL = 25 W
B) Pmax = (300/50)2 (25) = 900 W.

17. C) Quando RL = 25W temos:
vab = (300/50) 25 = 150 V
Pelo circuito original, temos que a corrente
da fonte é:
Is = (360 -150)/30 = 7 A
Logo, a fonte está fornecendo 7 x 360 =
2520 W ao circuito.
A porcentagem da potência que chega na
carga é:
(900/2520) x 100 = 35,71 %