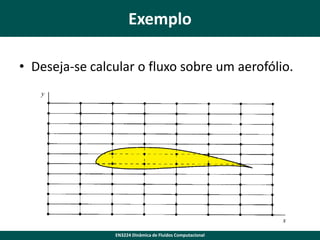
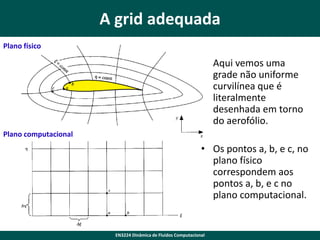
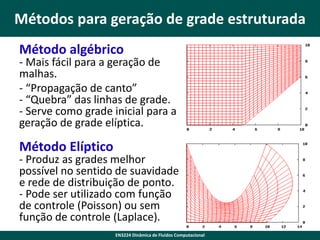
Este documento discute a geração de grades computacionais para simulações de dinâmica de fluidos. Explica que grades discretas uniformes são necessárias para métodos de diferenças finitas, mas que problemas reais nem sempre permitem grades uniformes diretas. Discute transformações de coordenadas para converter grades não uniformes em grades uniformes retangulares, permitindo que as equações sejam resolvidas numericamente. Também aborda a derivação matemática das transformações de coordenadas e suas implicações para as equações governantes de fluxo.















































![Programa exemplo
//--------------------------------------------------------------------------// executa um passo no sentido da solução
float dgrid()
{
int i,j;
float xm,ym,erro,mm;
float xx[MAXDIM][MAXDIM];
float yy[MAXDIM][MAXDIM];
mm = 0; erro = 0;
for(i=1;i<(n-1);i++)
for(j=1;j<(m-1);j++) {
xm = (xx[i-1][j] + xx[i+1][j] + xx[i][j-1] + xx[i][j+1])/4;
ym = (yy[i-1][j] + yy[i+1][j] + yy[i][j-1] + yy[i][j+1])/4;
erro += sqr(x[i][j] - xm) + sqr(y[i][j] - ym);
mm += 1.0;
x[i][j] = xm;
y[i][j] = ym;
}
erro = sqrt(erro) / mm;
return erro;
}
xi , j
xi 1, j xi 1, j xi , j 1 xi , j 1
EN3224 Dinâmica de Fluidos Computacional
4](https://image.slidesharecdn.com/cfd-aula06-140209143431-phpapp02/85/CFD-Aula-6-51-320.jpg)